一、前言

二、0/1背包

1、装箱问题（lanqiaoOJ题号763）

2、2022（2022年国赛填空题，lanqiaoOJ题号2186）

三、完全背包

1、小明的背包2（lanqiaoOJ题号1175）

四、分组背包

五、多重背包

一、前言

本文主要讲了0/1背包、完全背包、分组背包、多重背包的相关概念。

二、0/1背包

1、装箱问题（lanqiaoOJ题号763）

【题目描述】

有一个箱子容量为 V (正整数，0≤V≤20000)，同时有 n 个物品 (0<n≤30），每个物品有一个体积（正整数）。要求 n 个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

【输入描述】

输入第一行，一个整数，表示箱子容量。第二行，一个整数 n，表示有 n 个物品。接下来 n 行，分别表示这 n 个物品的各自体积。

【输出描述】

输出一行，表示箱子剩余空间。

0/1背包的简化版，不管物品的价格。把体积 (不是价格) 看成最优化目标：最大化体积。

dp=[0]*20010
V=int(input())
n=int(input())
c=[0]*40
for i in range(1,n+1):
    c[i]=int(input())
for i in range(1,n+1):
    for j in range(V,c[i]-1,-1):
        dp[j]=max(dp[j],dp[j-c[i]]+c[i])
print(V-dp[V])

2、2022（2022年国赛填空题，lanqiaoOJ题号2186）

【题目描述】

将 2022 拆分成 10 个互不相同的正整数之和，总共有多少种拆分方法？注意交换顺序视为同一种方法。注意交换顺序视为同一种方法。

例如：

2022 = 1000 + 1022

2022 = 1022 + 1000

视为同一种方法。

【思路】

题目求 10 个数的组合情况，这十个数相加等于 2022。因为是填空题可以不管运行时间，看起来可以用暴力 for 循环 10 次，加上剪枝。
然而暴力的时间极长，因为答案是：379187662194355221。
这一题其实是 0/1 背包：背包容量为 2022，物品体积为 1~2022，往背包中装 10 个物品，要求总体积为 2022，问一共有多少种方案。
与标准背包的区别：是求方案总数。

定义dp[][[]：dp[i][j][k]表示数字 1~i 取 j 个，和为 k 的方案数。

下面的分析沿用标准 0/1 背包的分析方法。

从 i-1 扩展到 i，分两种情况：

1）k ≥ i。数 i 可以要，也可以不要。

要 i。从 1~i-1 中取 j-1 个数，再取 i，等价于 dp[i-1][j-1][k-i]。

不要 i。从 1~i-1 中取 j 个数，等价于 dp[i-1][j][k]

合起来：dp[i][j][k] = dp[i-1][j][k] + dp[i-1][j-1][k-i]

2）k < i。由于数 i 比总和 k 还大，显然 i 不能用。有：dp[i][j][k] = dp[i-1][j][k]

【不用滚动数组】

1）k≥i。dp[i][j][k] = dp[i-1][j][k] + dp[i-1][j-1][k-i]

2）k<i。dp[i][j][k] = dp[i-1][j][k]

dp=[[[0]*2222 for i in range(11)] for j in range(2222)]
for i in range(0,2023):
    dp[i][0][0]=1       #特别注意这个初始化
for i in range(1,2023):
    for j in range(1,11):
        for k in range(1,2023):
            if k<i:
                dp[i][j][k]=dp[i-1][j][k]
            else:
                dp[i][j][k]=dp[i-1][j][k]+dp[i-1][j-1][k-i]
print(dp[2022][10][2022])

【用滚动数组】

1）k>=i。dp[i][j][k]=dp[i-1][j][k]+dp[i-1][j-1][k-i]

2）k<i。dp[i][j][k]=dp[i-1][j][k]

dp=[[0]*2222 for i in range(11)]
#for i in range(0,2023):
dp[0][0]=1               #特别注意这个初始化
for i in range(1,2023):
    for j in range(10,0,-1):    #10个数
        for k in range(i,2023): #k>=i
            dp[j][k]+=dp[j-1][k-i]
print(dp[10][2022])

三、完全背包

1、小明的背包2（lanqiaoOJ题号1175）

【题目描述】

小明有一个容量为 C 的背包。这天他去商场购物，商场一共有 N 种物品，第 i 种物品的体积为 ci,价值为 wi，每种物品都有无限多个。小明想知道在购买的物品总体积不超过 C 的情况下所能获得的最大价值为多少，请你帮他算算。

【输入描述】

输入第 1 行包含两个正整数 N,C，表示商场物品的数量和小明的背包容量。第 2~N+1 行包含 2 个正整数 c,w，表示物品的体积和价值。1<=N<=10^3，1<=C<=10^3，1<=ci, wi<=10^3。

【输出描述】

输出一行整数表示小明所能获得的最大价值。

思路和 0/1 背包类似。0/1 背包的每种物品只有 1 件，完全背包的每种物品有无穷多件，第 i 种可以装 0 件、1 件、2 件、C/ci 件。
定义 dp[i][j]：把前 i 种物品 (从第 1 种到第 i 种) 装入容量为 j 的背包中获得的最大价值。
把每个 dp[i][j] 都看成一个背包：背包容量为 j，装 1~i 这些物品。最后得到的 dp[N][C] 就是问题的答案：把 N 种物品装进容量 C 的背包的最大价值。
在 0/1 背包问题中，每个物品只有拿与不拿两种；而完全背包问题，需要考虑拿几个。

完全背包的代码和 0/1 背包的代码相似，只多了一个 k 循环，用来遍历每种物品拿几个。

def solve(n,C):
    for i in range(1,n+1):
        for j in range(0,C+1):
            if i==1:
                dp[i][j]=0
            else:
                dp[i][j]=dp[i-1][j]
            for k in range(0,j//c[i]+1):    #k*c[i]<=j  #在容量为j的背包中放几个
                dp[i][j]=max(dp[i][j],dp[i-1][j-k*c[i]]+k*w[i])
    return dp[n][C]

N=3011
dp=[[0]*N for j in range(N)]
w=[0]*N
c=[0]*N
n,C=map(int,input().split())
for i in range(1,n+1):
    c[i],w[i]=map(int,input().split())
print(solve(n,C))

复杂度：O(nC)

四、分组背包

分组背包问题：

有一些物品，把物品分为 n 组，其中第 i 组第 k 个物品体积是 c[i][k]，价值是 w[i][k]；
每组内的物品冲突，每组内最多只能选出一个物品；
给定一个容量为 C 的背包，问如何选物品，使得装进背包的物品的总价值最大。

【解题思路】

解题思路与 0/1 背包相似。

0/1 背包 dp[i][j]：把前 i 个物品 (从第1个到第i个) 装入容量为 j 的背包中获得的最大价值。
分组背包 dp[i][j]：把前 i 组物品装进容量 j 的背包 (每组最多选一个物品)，可获得的最大价值。
状态转移方程：dp[i][j] = max{dp[i-1][j]，dp[i-1][j-c[i][k]] + w[i][k]}

dp[i-1][j]表示第 i 组不选物品，dp[i-1][j-c[i][k]] 表示第 i 组选第 k 个物品。

求解方程需要做 i、j、k 的三重循环。

【滚动数组】

状态转移方程：dp[i][j]=max{dp[i-1][j], dp[i-1][j-c[i][k]]+w[i][k]}

用滚动数组，变为：dp[j]=max{dp[j], dp[j-c[i][k]]+w[i][k]}

dp=[0]*N
for i in range(1,n+1):      #遍历每个组
    for j in range(C,-1,-1):  #枚举容量
        for k in range(1,C+1):  #用k枚举第i组的所有物品
            if j>=c[i][k]:      #第k个物品能装进容量j的背包
                dp[j]=max(dp[j],dp[j-c[i][k]]+w[i][k])  #第i组第k个
print(dp[C])

五、多重背包

多重背包问题：

给定 n 种物品和一个背包，第 i 种物品的体积是 ci，价值为 wi，并且有 mi 个，背包的总容量为 C。
如何选择装入背包的物品，使得装入背包中的物品的总价值最大？
对比完全背包：一个容量为 C 的背包，有 N 种物品，第 i 种物品的体积为 ci，价值为 wi，每种物品都有无限多个。
两者非常相似。

【解题思路1：转化为0/1背包】

【解题思路2：直接DP】

状态转移方程：dp[i][j]=max{ dp[i-1][j], dp[i-1][j-k*c[i]]+k*w[i] }

用滚动数组，变为：dp[j]=max{ dp[j], dp[j-k*c[i]]+k*w[i] }

dp=[0]*N
for i in range(1,n+1):      #枚举物品
    for j in range(C,c[i]-1,-1):  #枚举背包容量
        for k in range(1,m[i]+1):  #用k遍历第i组的所有物品
            if j>=c[i]*k:           #第k个物品能装进容量j的背包
                dp[j]=max(dp[j],dp[j-k*c[i]]+k*w[i])
print(dp[C])

【解题思路3：二进制拆分优化】

一种简单而有效的技巧。

例如第 i 种物品有 mi=25 个，这 25 个物品放进背包的组合，有 0~25 的 26 种情况。
不过要组合成 26 种情况，其实并不需要 25 个物品。
根据二进制的计算原理，一个十进制整数 X，可以用 1、2、4、8、... 这些 2 的倍数相加得到，例如 25 = 16 + 8 + 1，这些 2 的倍数只有 logX 个。
题目中第 i 种物品有 mi 个，用 logmi 个数就能组合出 0~mi 种情况。总复杂度从O(C* $\sum_{i=1}^{n}mi$ )优化到O(C* $\sum_{i=1}^{n}\log mi$ )。

【二进制差分优化】

注意拆分的具体实现，不能全部拆成 2 的倍数，而是先按 2 的倍数从小到大拆，最后是一个小于等于最大倍数的余数。
保证拆出的数相加在 [1, mi] 范围内，不会大于mi。
例如 mi =25，把它拆成1、2、4、8、10，最后是余数 10，10<16=24，这 5 个数能组合成 1~25 内的所有数字，不会超过 25。
如果把 25 拆成 1、2、4、8、16，相加的范围就是 [1, 31] 了。

【例题】

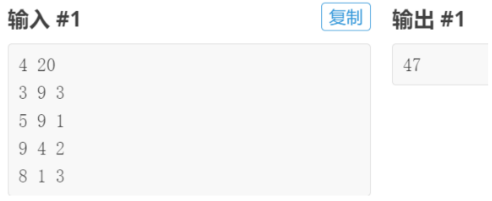
【输入描述】

第一行是整数 n 和 C，分别表示物品种数和背包的最大容量。接下来 n 行，每行三个整数 wi、ci、mi，分别表示第 i 个物品的价值、体积、数量。

【输出描述】

输出一个整数，表示背包不超载的情况下装入物品的最大价值。

N=100010
w=[0]*N
c=[0]*N
m=[0]*N
xw=[0]*N
xc=[0]*N
xm=[0]*N    #新的

n,C=map(int,input().split())
for i in range(1,n+1):
    w[i],c[i],m[i]=map(int,input().split())   #到此输入完毕

#以下是二进制拆分
xn=0        #二进制拆分后的新物品总数量
for i in range(1,n+1):
    j=1
    while j<=m[i]:      #例：m[i]=2
        m[i]-=j         #减去已经拆分的
        xn+=1
        xc[xn]=j*c[i]   #新物品的体积
        xw[xn]=j*w[i]
        j<<=1           #二进制枚举：1，2，4...
    if m[i]>0:          #最后一个是余数
        xn+=1
        xc[xn]=m[i]*c[i]
        xw[xn]=m[i]*w[i]

#以下是滚动数组版本的0/1背包
dp=[0]*N
for i in range(1,xn+1):     #枚举物品
    for j in range(C,xc[i]-1,-1):       #枚举背包容量
        dp[j]=max(dp[j],dp[j-xc[i]]+xw[i])
print(dp[C])

以上，DP背包问题

祝好