2023牛客寒假算法基础集训营4(7/13)

news2024/9/28 11:24:09

清楚姐姐学信息论

数学，只需要求x的y次方和y的x次方那个大选哪个，除了2和3时是3多，其他情况都是数越小能代表的数越多

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int x, y;
    cin >> x >> y;
    int maxx = max(x, y), minn = min(x, y);
    if (maxx == 3 && minn == 2) {
        cout << 3 << '\n';
    } else {
        cout << minn << '\n';
    }
    return 0;
}

清楚姐姐学构造

通过同余方程式可以看出，a是关于中点对称的，b的绝对值是关于中点对称的

因为

c[i]=a[i]+b[i]

所以

c[i]+c[n-1-i]=2*a[i]

c[n-1-i]-c[i]=2*b[i]

有了上述计算公式，发现c[i]+c[n-1-i]和c[n-1-i]-c[i]必须都是偶数才行，因为模数m一定是质数，也可知的是质数除了2都是奇素数，因此，除了2一定存在若干个m可以把c[i]+c[n-1-i]和c[n-1-i]-c[i]变成偶数来得到a[i],b[i]，但如果是2，则不可能，所以当m=2时如果存在奇数，则输出No

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, m;
    cin >> n >> m;
    vector<int> x, y;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    if (n == 1) {
        cout << "Yes\n";
        cout << a[0] << '\n';
        cout << "0\n";
        return 0;
    }
    if (m == 2) {
        for (int i = 0; i < n / 2; i++) {
            if ((a[i] + a[n - 1 - i]) % 2 == 1) {
                cout << "No\n";
                return 0;
            }
            int p = (a[i] + a[n - 1 - i]) / 2;
            x.push_back(p % m);
            if (((a[n - 1 - i] - a[i] + m) % m) % 2 == 1) {
                cout << "No\n";
                return 0;
            }
            p = ((a[n - 1 - i] - a[i] + m) % m) / 2;
            y.push_back(p % m);
        }
        if (n & 1) {
            x.push_back(a[n / 2]);
            y.push_back(0);
            cout << "Yes\n";
            for (int i = 0; i <= n / 2; i++) {
                cout << x[i] << " ";
            }
            for (int i = n / 2 - 1; i >= 0; i--) {
                cout << x[i] << " \n"[i == 0];
            }
            for (int i = 0; i <= n / 2; i++) {
                cout << m - y[i] << " ";
            }
            for (int i = n / 2 - 1; i >= 0; i--) {
                cout << y[i] << " \n"[i == 0];
            }
        } else {
            cout << "Yes\n";
            for (int i = 0; i < n / 2; i++) {
                cout << x[i] << " ";
            }
            for (int i = n / 2 - 1; i >= 0; i--) {
                cout << x[i] << " \n"[i == 0];
            }
            for (int i = 0; i < n / 2; i++) {
                cout << m - y[i] << " ";
            }
            for (int i = n / 2 - 1; i >= 0; i--) {
                cout << y[i] << " \n"[i == 0];
            }
        }
        return 0;
    }
    if (n & 1) {
        for (int i = 0; i < n / 2; i++) {
            int p = (a[i] + a[n - 1 - i]);
            while (p & 1) {
                p += m;
            }
            x.push_back(p / 2 % m);
            p = (a[n - 1 - i] - a[i] + m) % m;
            while (p & 1) {
                p += m;
            }
            y.push_back(p / 2 % m);
        }
        x.push_back(a[n / 2]);
        y.push_back(0);
        cout << "Yes\n";
        for (int i = 0; i <= n / 2; i++) {
            cout << x[i] << " ";
        }
        for (int i = n / 2 - 1; i >= 0; i--) {
            cout << x[i] << " \n"[i == 0];
        }
        for (int i = 0; i <= n / 2; i++) {
            cout << m - y[i] << " ";
        }
        for (int i = n / 2 - 1; i >= 0; i--) {
            cout << y[i] << " \n"[i == 0];
        }
    } else {
        for (int i = 0; i < n / 2; i++) {
            int p = (a[i] + a[n - 1 - i]);
            while (p & 1) {
                p += m;
            }
            x.push_back(p / 2 % m);
            p = (a[n - 1 - i] - a[i] + m) % m;
            while (p & 1) {
                p += m;
            }
            y.push_back(p / 2 % m);
        }
        x.push_back(a[n / 2]);
        y.push_back(0);
        cout << "Yes\n";
        for (int i = 0; i < n / 2; i++) {
            cout << x[i] << " ";
        }
        for (int i = n / 2 - 1; i >= 0; i--) {
            cout << x[i] << " \n"[i == 0];
        }
        for (int i = 0; i < n / 2; i++) {
            cout << m - y[i] << " ";
        }
        for (int i = n / 2 - 1; i >= 0; i--) {
            cout << y[i] << " \n"[i == 0];
        }
    }
    return 0;
}

清楚姐姐学01背包(Easy Version)

01背包，因为数据范围比较小，可以n的3次方暴力通过，即在01背包的基础上多了一维枚举去掉的是哪一个蝴蝶结，即dp[i][j]表示的是去掉第i个蝴蝶结后的n-1个蝴蝶结中，体积为j的最大好看程度总和

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, m;
    cin >> n >> m;
    vector<pair<int, int>> a(n + 1);
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        cin >> a[i].first >> a[i].second;
        sum = max(sum, a[i].second);
    }
    vector<int> dp1(m + 2);
    for (int i = 1; i <= n; i++) {
        for (int j = m; j >= a[i].first; j--) {
            dp1[j] = max(dp1[j], dp1[j - a[i].first] + a[i].second);
        }
    }
    vector<vector<int>> dp(n + 1, vector<int> (m + 2));
    int maxx = *max_element(dp1.begin(), dp1.end());
    for (int k = 1; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            if (i == k) {
                continue;
            }
            for (int j = m; j >= a[i].first; j--) {
                dp[k][j] = max(dp[k][j], dp[k][j - a[i].first] + a[i].second);
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        int max1 = *max_element(dp[i].begin(), dp[i].end());
        if (max1 != maxx) {
            cout << "0\n";
        } else {
            int ans = 1e18;
            for (int j = 0; j <= m - a[i].first; j++) {
                ans = min(ans, maxx - dp[i][j] + 1 - a[i].second);
            }
            cout << ans << '\n';
        }
    }
    return 0;
}

清楚姐姐打怪升级

根据题意可以发现，当a>=h[i]的时候，可以一秒秒杀怪，当h[i]>a的时候，能杀死怪的前提是a-v[i]*t>0，否则每次攻击后怪都能把血量恢复起来

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    LL n, t, a;
    cin >> n >> t >> a;
    vector<pair<LL, LL>> x(n);
    LL ans = 0;
    for (int i = 0; i < n; i++) {
        cin >> x[i].first >> x[i].second;
    }
    for (int i = 0; i < n; i++) {
        if (i == 0) {
            if (x[i].first <= a) {
                ans = 1;
            } else {
                ans = 1;
                x[i].first -= a;
                if (x[i].second * t >= a) {
                    ans = -1;
                    break;
                } else {
                    LL p = a - x[i].second * t, z = (x[i].first + p - 1) / p;
                    ans += z * t;
                }
            }
        } else {
            if (x[i].first <= a) {
                ans += t;
            } else {
                x[i].first -= a;
                ans += t;
                if (x[i].second * t >= a) {
                    ans = -1;
                    break;
                } else {
                    LL p = a - x[i].second * t, z = (x[i].first + p - 1) / p;
                    ans += z * t;
                }
            }
        }
    }
    cout << ans << '\n';
    return 0;
}

清楚姐姐学树状数组

根据题意，二叉树中序遍历的结果是1~n，所以只需要考虑前序和后序遍历的结果。

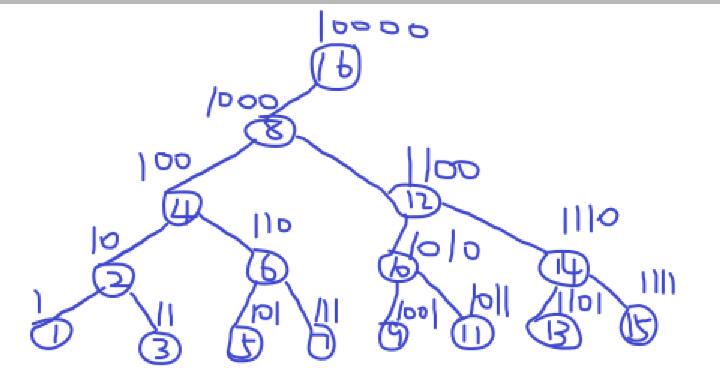
根据这张图我们可以看出，我们能够计算出一个数到根的路径，即对于一个从低位往高位走的二进制，如果当前位为1的，如果他的高一位的二进制位仍然是1，那么去往根的下一个结点就是把这一位变成0，如果他的高一位的二进制位为0，去往根的下一个结点就是在加一个lowbit，从而我们得到了从某一结点到根的路径，这样我们就可以从根再往要求的结点走，可知，如果当前结点的值大于x，说明x在左子树，否则在右子树上，对于前序遍历，往左子树走，步数只需要+1，而往右子树走的话需要把左子树的儿子节点个数及其父节点都加上，也就是lowbit(当前节点编号)。再考虑后序遍历，如果当前节点编号小于x，说明x在右子树，因为是后序遍历，所以需要加上左子树的儿子节点个数，如果走到了x，并且x为奇数，可知x为叶子节点，不存在子树，不需要操作，如果x为偶数，说明x不是叶子节点，存在子树，所以需要加上x的儿子节点个数，即(lowbit(x)-1)*2

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
#define lowbit(x) (x & (-x))
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    map<int, int> mp;
    int res = 1;
    mp[1] = 0;
    for (int i = 1; i <= 61; i++) {
        res <<= 1;
        mp[res] = i;
    }
    int k, q;
    cin >> k >> q;
    while (q--) {
        int x, y;
        cin >> x;
        if (x == (1LL << k)) {
            cout << 1 << " " << (1LL << k) << " " << (1LL << k) << '\n';
            continue;
        }
        y = x;
        int ans = 1, ans1 = 1;
        vector<int> z;
        z.push_back(x);
        for (int i = mp[lowbit(x)] + 1; i <= 61; i++) {
            if (x >= (1LL << k)) {
                break;
            }
            if (x >> i & 1 && x >> (i - 1) & 1) {
                x -= lowbit(x);
                z.push_back(x);
            } else if ((x >> i) % 2 == 0 && (x >> (i - 1)) & 1) {
                x += lowbit(x);
                z.push_back(x);
            } else {
                break;
            }
        }
        int len = z.size();
        for (int i = len - 1; i > 0; i--) {
            if (y > z[i]) {
                ans += lowbit(z[i]);
            } else {
                ans++;
            }
        }
        for (int i = len - 1; i >= 0; i--) {
            if (y > z[i]) {
                ans1 += lowbit(z[i]) - 1;
            } else if (y == z[i] && y % 2 == 0) {
                ans1 += (lowbit(z[i]) - 1) * 2;
            }
        }
        cout << ans << " " << y << " " << ans1 << "\n";
    }
    return 0;
}

清楚姐姐的三角形I

因为

Va=Lb+Lc

Vb=La+Lc

Vc=La+Lb

所以联立可得

2*La=Vb+Vc-Va

2*Lb=Va+Vc-Vb

2*Lc=Va+Vb-Vc

因此，如果有奇数则不可能成立，并且如果边有小于等于0的也不成立，两条较小的边的和必须大于最大的边，注意输出顺序

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    while (T--) {
        LL x, y, z;
        cin >> x >> y >> z;
        vector<LL> a(3);
        LL sum = x + y + z;
        if (sum % 2 == 1) {
            cout << "No\n";
            continue;
        }
        sum /= 2;
        LL xx = sum - x, yy = sum - y, zz = sum - z;
        a[0] = sum - x;
        a[1] = sum - y;
        a[2] = sum - z;
        sort(a.begin(), a.end());
        if (a[0] <= 0) {
            cout << "No\n";
        } else if (a[0] + a[1] <= a[2]) {
            cout << "No\n";
        } else {
            cout << "Yes\n";
            cout << xx << " " << yy << " " << zz << '\n';
        }
    }
    return 0;
}

清楚姐姐的三角形II

很多种构造方式，只要不满足三角形即可

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;
    cin >> n;
    vector<int> a(45);
    a[1] = 1, a[2] = 1;
    for (int i = 3; i <= 44; i++) {
        a[i] = a[i - 1] + a[i - 2];
    }
    int x = n / 44, y = n % 44;
    for (int i = 0; i < x; i++) {
        for (int j = 1; j <= 44; j++) {
            cout << a[j] << " ";
        }
    }
    for (int i = 1; i <= y; i++) {
        cout << a[i] << " ";
    }
    cout << '\n';
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/186672.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ESP32 Arduino学习篇 (三) 蓝牙

ESP32 Arduino学习篇 (三) 蓝牙

简介&#xff1a;1.1蓝牙分类经典蓝牙我们一般说的是BT&#xff0c;低功耗蓝牙我们一般说成BLE。当设备支持蓝牙4.0时&#xff0c;还得进一步确认设备是支持BT单模、BLE单模还是BT和BLE都支持的双模。低功耗蓝牙 (BLE)&#xff1a; 支持蓝牙协议4.0或更高的模块。主打低功耗&am…
阅读更多...
手上有了这些工具，明天争取6点下班！

手上有了这些工具，明天争取6点下班！

一个优秀的开发者&#xff0c;一定是会利用各种工具来提升自己的开发效率。这段时间&#xff0c;我开始分享优质提升开发效率的工具&#xff0c;集成效率工具&#xff0c;开源集成网站等等&#xff0c;朋友们一直在催更&#xff0c;我知道你很急&#xff0c;但是你先别急&#…
阅读更多...
最短路径算法刷题笔记

最短路径算法刷题笔记

Dijkstra最短路算法 带负权则无法处理&#xff0c;不能使用Dijkstra算法 Dijkstra算法以 点 出发。D——点从剩下的点里的最短路dis最小的出发 SPFA单源最短路算法 算是bellman-ford算法 对于稀疏图来说&#xff0c;比Dijkstra算法快 SPFA算法可以用于有负权图有负环则不行 …
阅读更多...
文档扫描OCR识别_积累

文档扫描OCR识别_积累

opecncv和python的积累cv2.resize()功能&#xff1a;对图像尺寸调整为指定大小dst cv2.resize(src, dsize, interpolationNone)各参数释义&#xff1a;scr&#xff1a; 输入图像dst: 输出图像dsize&#xff1a; 输出图像的尺寸&#xff0c;为元组格式(x, y)&#xff0c;(300, …
阅读更多...
MySQL基础（2）—— 初识MySQL

MySQL基础（2）—— 初识MySQL

文章目录客户端 - 服务器架构MySQL的可执行文件1、在命令行解释器中运行可执行文件2、服务器程序和客户端程序2.1 服务器程序 mysqld2.2 客户端程序 mysql注意事项1、客户端 - 服务器连接注意事项2、SQL语句使用注意事项客户端 - 服务器架构 MySQL当中存在客户端和服务器&…
阅读更多...
不知道该学那一个语言？一文带你了解三门语言

不知道该学那一个语言？一文带你了解三门语言

名字&#xff1a;阿玥的小东东 学习&#xff1a;Python。正在学习c 主页&#xff1a;阿玥的小东东 目录 粉丝留言&#xff0c;回答问题 1.首先&#xff0c;初步了解 2.再明确自己要拿编程做什么 3.详细介绍以及建议 4.劝告 5.总结 1.如果你是一个初学者 2.你是个老手 …
阅读更多...
vulnhub之COFFEE ADDICTS: 1

vulnhub之COFFEE ADDICTS: 1

1.信息收集 输入arp-scan 192.168.239.0/24发现192.168.239.168主机存活。 使用nmap对目标主机192.168.239.168进行端口收集,&#xff0c;发现存活端口&#xff1a;22、80。 访问http://192.168.239.168/&#xff0c;提示将coffeeaddicts.thm加入到/etc/hosts中 加入之后访…
阅读更多...
docker 安装启动异常

docker 安装启动异常

问题现象1 yum install docker -y #安装docker后&#xff0c;在启动docker时出现 排查过程 查看系统日志下面软件运行日志messages日志&#xff0c;出现如下错误 在docker的配置文件种有异常的文件符号存在&#xff0c;那么接下来就百度一下正常的docker的配置文件是如何的…
阅读更多...
【HBase——陌陌海量存储案例】6. 预分区表

【HBase——陌陌海量存储案例】6. 预分区表

6.5 预分区表 默认创建表的方式&#xff0c;则HBase顺序写入可能会受到RegionServer热点的影响。对行键进行加盐可以解决热点问题。在HBase中&#xff0c;可以使用两种方式&#xff1a; 1.ROWKEY预分区 2.加盐指定数量分区 6.5.1 ROWKEY预分区 按照用户ID来分区&#xff0c;一…
阅读更多...
Docker 入门详解！新手也能看懂！

Docker 入门详解！新手也能看懂！

接下来通过4方面来初步了解docker docker介绍docker架构docker镜像操作docker容器操作 一、docker介绍 容器技术 计算机的世界中&#xff0c;容器拥有一段漫长且传奇的历史。容器与管理程序虚拟化 &#xff08;hypervisor virtualization&#xff0c;HV&#xff09;有所不同…
阅读更多...
postman断言使用总结

postman断言使用总结

一、断言的概念一个完整的接口测试包括&#xff1a;请求——>获取响应结果——>断言断言&#xff1a;实际结果与预期结果的校验二、断言的作用通过实际结果与预期结果的对比&#xff0c;来判断接口测试用例是否通过&#xff1b;对比结果一致则通过&#xff0c;对比结果不…
阅读更多...
webgl绘制图形API——drawArrays、drawElements

webgl绘制图形API——drawArrays、drawElements

文章目录前言gl.drawArrays()——按顶点绘制可绘制基本类型绘制矩形和圆形gl.drawElements()——按索引绘制使用规范绘制矩形总结前言 gl.drawArrays()作为webgl中常用的函数图形绘制方法&#xff0c;可以在浏览器按照指定的模式绘制图形&#xff0c;与之相对的gl.drawElement…
阅读更多...
字节跳动测试岗面试挂在2面，复盘后，我总结了失败原因，决定再战一次...

字节跳动测试岗面试挂在2面，复盘后，我总结了失败原因，决定再战一次...

先说下我基本情况&#xff0c;本科不是计算机专业&#xff0c;现在是学通信&#xff0c;然后做图像处理&#xff0c;可能面试官看我不是科班出身没有问太多计算机相关的问题&#xff0c;因为第一次找工作&#xff0c;字节的游戏专场又是最早开始的&#xff0c;就投递了&#xf…
阅读更多...
Java图形化界面---JSplitPane和JTabbedPane

Java图形化界面---JSplitPane和JTabbedPane

目录 一、JSplitPane &#xff08;1&#xff09;JSplitPane的介绍 &#xff08;2&#xff09;JSplitPane的使用步骤 &#xff08;3&#xff09;案例 二、JTabbedPane &#xff08;1&#xff09;JTabbedPane的介绍 &#xff08;2&#xff09;JTabbedPane的使用步骤 &…
阅读更多...
CSS样式基础内容6

CSS样式基础内容6

目录 定位 为什么需要定位&#xff1f; 定位的四种方式 静态定位 相对定位 绝对定位&#xff08;脱标&#xff09; 子绝父相 固定定位&#xff08;脱标&#xff09; 固定定位---固定到版心右侧 粘性定位 定位的叠放顺序z-index 绝对定位盒子水平垂直居中 定位特殊特…
阅读更多...
C#/WPF入门到多项目实战开发教程2——

C#/WPF入门到多项目实战开发教程2——

登录界面 布局 右上角退出按钮 编辑图标和名称 用户名设置 布局 用户名框设置 密码框设置&#xff0c;使用模板进行设置 验证码框设置&#xff0c;使用模板进行设置 登录按钮 创建登录模板按钮 绑定模板 失败提醒 第三方登录设置 使用字体图标去替代一般图标&#xff0c;字体…
阅读更多...
QThread的应用——在线程里面更新QProgressBar进度条

QThread的应用——在线程里面更新QProgressBar进度条

在线程里面更新QProgressBar进度条 编写QT软件的时候&#xff0c;经常会遇到点击某个按钮&#xff0c;进行一个比较耗时的计算。为了在计算过程中&#xff0c;软件界面就继续响应用户的点击&#xff0c;不会有卡死的感觉&#xff0c;一般会将这个耗时的计算放在另外一个线程里…
阅读更多...
“打家劫舍”系列总结，偷不偷这个房间呢？（Java实现）

“打家劫舍”系列总结，偷不偷这个房间呢？（Java实现）

目录 前言 一、打家劫舍 ——>房子是线性的 1.1、dp定义 1.2、递推公式 1.3、初始化 1.4、遍历顺序 1.5、解题代码 二、打家劫舍II ——>房子是环型 2.1、分析 2.2、解题代码 三、打家劫舍III ——>房子是树形 3.1、dp含义 3.2、递推公式 3.3、解题代码…
阅读更多...
【Trusted Firmware-A 移植】

【Trusted Firmware-A 移植】

Trusted Firmware-A 移植Trusted Firmware-A 简介步骤一、解压标准 tf-a 源码包,进入 tf-a 源码目录下&#xff1a;二、将 ST 官方补丁文件打到 tf-a 源码中&#xff1a;三、配置交叉编译工具链四、添加设备树文件五、编译源码六、固件烧写结果Trusted Firmware-A 简介 嵌入式…
阅读更多...
Magisk工具使用指南

Magisk工具使用指南

对于一般玩机用户，Magisk官方提供的发布版本即可满足要求，但对于高级开发者来说这远远不够，我们不仅仅是满足于使用，更要学会定制面具，最好的能完全理解面具的核心架构以便于自己也能写出来一套和面具差不多的工具，这才是我们研究面具最根本的原因所在。因为做移动安全，…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023