Dijkstra最短路算法

带负权则无法处理，不能使用Dijkstra算法

Dijkstra算法以 点 出发。D——点从剩下的点里的最短路dis最小的出发

SPFA单源最短路算法

算是bellman-ford算法

对于稀疏图来说，比Dijkstra算法快
SPFA算法可以用于有负权图有负环则不行
一般能用Dijstra算法则用Dijstra算法

SPFA算法以边出发bellman-ford，b——边 SPFA用到队列，将源点相关联的点放到队列中然后再从队列中的点取寻找

SPFA判断负环

Floyd多源最短路算法

只能处理不带负边权的图
用邻接矩阵而不是邻接表

注意循环的顺序：

1. 先循环k
2. 再循环i
3. 最后才是j

可以理解为：先固定一个点，这个点是否出现最短路中。然后再固定 i , j 观察路径，通过枚举出任意两个点的路径，然后再看固定的k点是否出现在其中这样的循环效率更高

这段代码的基本思想就是：最开始只允许经过1号顶点进行中转，接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从i号顶点到j号顶点只经过前k号点的最短路程。

次短路问题

灾后重建

B 地区在地震过后，所有村庄都造成了一定的损毁，而这场地震却没对公路造成什么影响。但是在村庄重建好之前，所有与未重建完成的村庄的公路均无法通车。换句话说，只有连接着两个重建完成的村庄的公路才能通车，只能到达重建完成的村庄。

给出 B 地区的村庄数 $N$，村庄编号从 $0$ 到 $N-1$，和所有 $M$ 条公路的长度，公路是双向的。并给出第 $i$ 个村庄重建完成的时间 $t_i$，你可以认为是同时开始重建并在第 $t_i$ 天重建完成，并且在当天即可通车。若 $t_i$ 为 $0$ 则说明地震未对此地区造成损坏，一开始就可以通车。之后有 $Q$ 个询问 $(x,y,t)$，对于每个询问你要回答在第 $t$ 天，从村庄 $x$ 到村庄 $y$ 的最短路径长度为多少。如果无法找到从 $x$ 村庄到 $y$ 村庄的路径，经过若干个已重建完成的村庄，或者村庄 $x$ 或村庄 $y$ 在第 $t$ 天仍未重建完成，则需要返回 -1。

输入格式

第一行包含两个正整数$N,M$，表示了村庄的数目与公路的数量。

第二行包含$N$个非负整数$t_0,t_1,\dots ,t_{N-1}$，表示了每个村庄重建完成的时间，数据保证了$t_0\le t_1\le \dots \le t_{N-1}$。

接下来$M$行，每行$3$个非负整数$i,j,w$，$w$为不超过$10000$的正整数，表示了有一条连接村庄$i$与村庄$j$的道路，长度为$w$，保证$i\ne j$，且对于任意一对村庄只会存在一条道路。

接下来一行也就是$M+3$行包含一个正整数$Q$，表示$Q$个询问。

接下来$Q$行，每行$3$个非负整数$x,y,t$，询问在第$t$天，从村庄$x$到村庄$y$的最短路径长度为多少，数据保证了$t$是不下降的。

输出格式

共$Q$行，对每一个询问$(x,y,t)$输出对应的答案，即在第$t$天，从村庄$x$到村庄$y$的最短路径长度为多少。如果在第t天无法找到从$x$村庄到$y$村庄的路径，经过若干个已重建完成的村庄，或者村庄x或村庄$y$在第$t$天仍未修复完成，则输出$-1$。

样例输入 #1

4 5
1 2 3 4
0 2 1
2 3 1
3 1 2
2 1 4
0 3 5
4
2 0 2
0 1 2
0 1 3
0 1 4

样例输出 #1

-1
-1
5
4

提示

对于$30\%$的数据，有$N\le 50$；

对于$30\%$的数据，有$t_i=0$，其中有$20\%$的数据有$t_i=0$且$N>50$；

对于$50\%$的数据，有$Q\le 100$；

对于$100\%$的数据，有$N\le 200$，$M\le N\times (N-1)/2$，$Q\le 50000$，所有输入数据涉及整数均不超过$100000$。

思路

• 比较典型的 Floyd 算法问题
• 具体见代码注释吧

题解

#include<bits/stdc++.h>
using namespace std;
int n,m,a[205],f[205][205];
inline void update(int k){
	for(int i=0;i<n;i++)
	for(int j=0;j<n;j++)
	f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=0;i<n;i++)
	scanf("%d",a+i);
	for(int i=0;i<n;i++)
	for(int j=0;j<n;j++) f[i][j]=1e9;
	for(int i=0;i<n;i++) f[i][i]=0;
	int s1,s2,s3;
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&s1,&s2,&s3);
		f[s1][s2]=f[s2][s1]=s3;
	}
	int q;
	scanf("%d",&q);
	int now=0;
	for(int i=1;i<=q;i++){
		scanf("%d%d%d",&s1,&s2,&s3);
		while(a[now]<=s3&&now<n){ //因为题目中说明了是按照时间顺序的，所以不用排序。用now作Floyd算法中的k，因为在给出的询问中是按时间顺序的，所以时间早的，也早就被更新了。只用一步一步更新后来的时间对应的城镇即可
			update(now); 
			now++;
		}
		if(a[s1]>s3||a[s2]>s3)cout<<-1<<endl;
		else {
			if(f[s1][s2]==1e9)cout<<-1<<endl;
			else cout<<f[s1][s2]<<endl;
		}
	}
} 

邮递员送信

有一个邮递员要送东西，邮局在节点 $1$。他总共要送 $n-1$ 样东西，其目的地分别是节点 $2$ 到节点 $n$。由于这个城市的交通比较繁忙，因此所有的道路都是单行的，共有 $m$ 条道路。这个邮递员每次只能带一样东西，并且运送每件物品过后必须返回邮局。求送完这 $n-1$ 样东西并且最终回到邮局最少需要的时间。

输入格式

第一行包括两个整数，$n$ 和 $m$，表示城市的节点数量和道路数量。

第二行到第 $(m+1)$ 行，每行三个整数，$u,v,w$，表示从 $u$ 到 $v$ 有一条通过时间为 $w$ 的道路。

输出格式

输出仅一行，包含一个整数，为最少需要的时间。

样例输入 #1

5 10
2 3 5
1 5 5
3 5 6
1 2 8
1 3 8
5 3 4
4 1 8
4 5 3
3 5 6
5 4 2

样例输出 #1

83

提示

对于 $30\%$ 的数据，$1\le n\le 200$。

对于 $100\%$ 的数据，$1\le n\le 10^3$，$1\le m\le 10^5$，$1\le u,v\le n$，$1\le w\le 10^4$，输入保证任意两点都能互相到达。

思路

• 看完题目，可以得知：要实现邮递员从 1 到 n-1 是比较简单的，基本就是套模板
• 根据题目不难得知是有向边。从 n-1 到 1 ，如果用spfa算法遍历 n-1 到 1 的话，时间复杂度是O(n³)，大概率TLE。所以不先考虑这个方法
• 考虑建立反图：在邮递员回去的这段中，将图上所有的边取反向，那么从 1 到 n-1 的最短路即是 非反图中 n-1 到 1 的最短路

题解

#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
int n,m,u[100005],v[100005],w[100005],dis[1005],ans=0;
void ford(){
	for(int i=1;i<=n;i++)dis[i]=INF;
	dis[1]=0;
	for(int k=1;k<=n-1;k++){
		for(int i=1;i<=m;i++){
			if(dis[v[i]]>dis[u[i]]+w[i]){
				dis[v[i]]=dis[u[i]]+w[i];
			}
		}
	}
	for(int i=1;i<=n;i++)ans+=dis[i];
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)scanf("%d%d%d",&u[i],&v[i],&w[i]);
	ford();
	for(int i=1;i<=m;i++) swap(u[i],v[i]);
	ford();
	printf("%d\n",ans);
}

【模板】单源最短路径（标准版）

2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 归程 一题里非常熟练地使用了一个广为人知的算法求最短路。

然后呢？

$100\to 60$；

$\text{Ag}\to \text{Cu}$；

最终，他因此没能与理想的大学达成契约。

小 F 衷心祝愿大家不再重蹈覆辙。

---

给定一个 $n$ 个点，$m$ 条有向边的带非负权图，请你计算从 $s$ 出发，到每个点的距离。

数据保证你能从 $s$ 出发到任意点。

输入格式

第一行为三个正整数 $n,m,s$。
第二行起 $m$ 行，每行三个非负整数 $u_i,v_i,w_i$，表示从 $u_i$ 到 $v_i$ 有一条权值为 $w_i$ 的有向边。

输出格式

输出一行 $n$ 个空格分隔的非负整数，表示 $s$ 到每个点的距离。

样例输入 #1

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

样例输出 #1

0 2 4 3

提示

样例解释请参考 数据随机的模板题。

$1\le n\le 10^5$；

$1\le m\le 2\times 10^5$；

$s=1$；

$1\le u_i,v_i\le n$；

$0\le w_i\le 10^9$,

$0\le \sum w_i\le 10^9$。

思路

• 模板题，用好Dijkstra算法+堆优化
• 虽然Dijkstra算法思想好理解，但是实现起来还是有点复杂的
• 具体看代码注释

题解

#include<bits/stdc++.h>
const int MaxN = 100010, MaxM = 500010;
struct edge{
    int to, dis, next;
};
edge e[MaxM];
int head[MaxN], dis[MaxN], cnt;
bool vis[MaxN];
int n, m, s;
inline void add_edge( int u, int v, int d ){
    cnt++;
    e[cnt].dis = d;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt; //这个head以链表的形式连接点，分析下面给出的图就会发现，通过head数组即可找到u点连接的所有点
}

struct node{
    int dis;
    int pos;
    bool operator <( const node &x )const
    {
        return x.dis < dis;
    }
};

std::priority_queue<node> q;

inline void dijkstra(){
    dis[s] = 0;
    q.push( ( node ){0, s} );
    while( !q.empty() ){
        node tmp = q.top();
        q.pop();
        int x = tmp.pos, d = tmp.dis;
        if( vis[x] )continue;
        vis[x] = 1;
        for( int i = head[x]; i; i = e[i].next ){     //循环：i=e[i].next就可以发现相关联的点都被连接起来了
            int y = e[i].to;
            if( dis[y] > dis[x] + e[i].dis ){
                dis[y] =std::min(dis[y],dis[x] + e[i].dis);
                if( !vis[y] ) q.push( ( node ){dis[y], y} );
            }
        }
    }
}


int main(){
    scanf( "%d%d%d", &n, &m, &s );
    for(int i = 1; i <= n; ++i)dis[i] = 0x7fffffff;
    for( register int i = 0; i < m; ++i ){
        register int u, v, d;
        scanf( "%d%d%d", &u, &v, &d );
        add_edge( u, v, d );
    }
    dijkstra();
    for( int i = 1; i <= n; i++ )
        printf( "%d ", dis[i] );
    return 0;
}

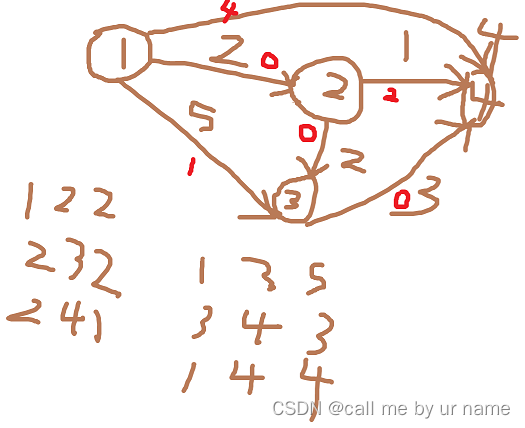
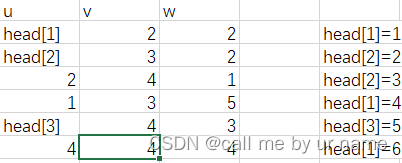
感觉Dijkstra算法代码和SPFA代码有些相似之处

【模板】负环

给定一个 $n$ 个点的有向图，请求出图中是否存在从顶点 $1$ 出发能到达的负环。

负环的定义是：一条边权之和为负数的回路。

输入格式

本题单测试点有多组测试数据

输入的第一行是一个整数 $T$，表示测试数据的组数。对于每组数据的格式如下：

第一行有两个整数，分别表示图的点数 $n$ 和接下来给出边信息的条数 $m$。

接下来 $m$ 行，每行三个整数 $u,v,w$。

• 若 $w\ge 0$，则表示存在一条从 $u$ 至 $v$ 边权为 $w$ 的边，还存在一条从 $v$ 至 $u$ 边权为 $w$ 的边。
• 若 $w<0$，则只表示存在一条从 $u$ 至 $v$ 边权为 $w$ 的边。

输出格式

对于每组数据，输出一行一个字符串，若所求负环存在，则输出 YES，否则输出 NO。

样例输入 #1

2
3 4
1 2 2
1 3 4
2 3 1
3 1 -3
3 3
1 2 3
2 3 4
3 1 -8

样例输出 #1

NO
YES

提示

数据规模与约定

对于全部的测试点，保证：

• $1\le n\le 2\times 10^3$，$1\le m\le 3\times 10^3$。
• $1\le u,v\le n$，$-10^4\le w\le 10^4$。
• $1\le T\le 10$。

提示

请注意，$m$ 不是图的边数。

思路

• 我们发现第$i$轮迭代实际是在计算最短路包含$i$条边的结点。所以我们用$cnt[x]$表示1到$x$的最短路包含的边数，$cnt$[1]=0。每次用$dis[x]+w(x,y)$更新$dis[y]$，也用$cnt[x]$+1更新$cnt[y]$。此过程中若出现$cnt[y]$≥$n$则图中有负环。最坏情况复杂度也是$O(nm)$
• 也可以用另一种方式理解：$1$到$x$的最短路上的边数一定不多于$n-1$。否则至少有一个结点被重复经过，这说明存在环，且经过该环能更新该结点的$dis$值，即存在负环
• SPFA也可以通过记录每个点的入队次数判断负环，若有节点入队次数 ≥n，则有负环。这种方式效率会略低
• 具体看代码解析

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e3+10;
const int maxm=6e3+10;
int n,m;
struct Edge{
	int to,w,next;
}edge[maxm];        
int head[maxn],tot;
inline void Init(){     
	for(int i=0;i<maxn;i++) head[i]=0;
	tot=0;
}
inline void addedge(int u,int v,int w){
	edge[++tot].to=v;
	edge[tot].w=w;
	edge[tot].next=head[u];
	head[u]=tot;                      //仍然是用head来作为链表存储
}
queue<int> Q;
int dis[maxn],vis[maxn],cnt[maxn];
bool spfa(){
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	memset(cnt,0,sizeof(cnt));
	dis[1]=0; vis[1]=true;
	Q.push(1);
	while(!Q.empty()){
		int x=Q.front();
		Q.pop();
		vis[x]=false;                  //因为环，所以弹出x后将vis[x]置于未标记
		for(int i=head[x];i;i=edge[i].next){
			int y=edge[i].to,z=edge[i].w;
			if(dis[y]>dis[x]+z){
				dis[y]=dis[x]+z;  
				cnt[y]=cnt[x]+1;  
				if(cnt[y]>=n) return true;              //相比上一题，这题就是多加了一步判断负环
				if(!vis[y]) Q.push(y),vis[y]=true;      
			}
		}
	}
	return false;
}
int main(){
	int T;
	scanf("%d",&T);
	while(T--){
		Init();
		scanf("%d%d",&n,&m);
		for(int i=1;i<=m;i++){
			int u,v,w;
			scanf("%d%d%d",&u,&v,&w);
			addedge(u,v,w);
			if(w>=0) addedge(v,u,w);
		}
		puts(spfa()?"YES":"NO");            //这个输出方式很新颖
	}
}

集合位置

每次有大的活动，大家都要在一起“聚一聚”，不管是去好乐迪，还是避风塘，或者汤姆熊，大家都要玩的痛快。还记得心语和花儿在跳舞机上的激情与释放，还记得草草的投篮技艺是如此的高超，还记得狗狗的枪法永远是’S’……还有不能忘了，胖子的歌声永远是让我们惊叫的！！

今天是野猫的生日，所以想到这些也正常，只是因为是上学日，没法一起去玩了。但回忆一下那时的甜蜜总是一种幸福嘛。。。

但是每次集合的时候都会出现问题！野猫是公认的“路盲”，野猫自己心里也很清楚，每次都提前出门，但还是经常迟到，这点让大家很是无奈。后来，野猫在每次出门前，都会向花儿咨询一下路径，根据已知的路径中，总算能按时到了。

现在提出这样的一个问题：给出 $n$ 个点的坐标，其中第一个为野猫的出发位置，最后一个为大家的集合位置，并给出哪些位置点是相连的。野猫从出发点到达集合点，总会挑一条最近的路走，如果野猫没找到最近的路，他就会走第二近的路。请帮野猫求一下这条第二最短路径长度。

输入格式

第一行是两个整数 $n(1\le n\le 200)$ 和 $m$，表示一共有 $n$ 个点和 $m$ 条路，以下 $n$ 行每行两个数 $x_i$，$y_i$，$(-500\le x_i,y_i\le 500),$ 代表第 $i$ 个点的坐标，再往下的 $m$ 行每行两个整数 $p_j$，$q_j,(1\le p_j,q_j\le n)$，表示两个点相通。

输出格式

只有一行包含一个数，为第二最短路线的距离（保留两位小数），如果存在多条第一短路径，则答案就是第一最短路径的长度；如果不存在第二最短路径，输出 -1。

样例输入 #1

3 3
0 0
1 1
0 2
1 2
1 3
2 3

样例输出 #1

2.83

思路

• 找出最短路，然后枚举删除最短路上的每一条边，即可知道次短路的长度

题解

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define pdi pair<double,int>
using namespace std;
struct Node{
	double x,y;
	int head;
	double dis;
	int prev; 
}node[205];
struct Edge{
	int next,to; 
	double len; 
}edge[50005];
int n,m,cnt;
double ans=INF<<1;
double calc(double a,double b,double c,double d){
	return (double)sqrt(double(a-c)*double(a-c)+double(b-d)*double(b-d));
}
void addEdge(int u,int v,double w){
	edge[++cnt].len=w;
	edge[cnt].to=v;
	edge[cnt].next=node[u].head;
	node[u].head=cnt;
}
void Dijkstra(int x,int y){
	for(int i=1;i<=n;i++) node[i].dis=INF;
	node[1].dis=0;
	priority_queue<pdi,vector<pdi>,greater<pdi> >q;
	q.push({0,1});
	while(q.size()){
		pdi tmp=q.top();
		q.pop();
		double d=tmp.first;
		int u=tmp.second;
		if(node[u].dis!=d)continue;
		for(int e=node[u].head;e;e=edge[e].next){
			int v=edge[e].to;
			if((u==x&&v==y)||(u==y&&v==x))continue;
			if(node[v].dis<=d+edge[e].len) continue;
			if(x==-1&&y==-1)node[v].prev=u;
			node[v].dis=d+edge[e].len;
			q.push({node[v].dis,v});
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%lf%lf",&node[i].x,&node[i].y);
	}
	for(int i=1,u,v;i<=m;i++){
		scanf("%d%d",&u,&v);
		double w=calc(node[u].x,node[u].y,node[v].x,node[v].y);
		addEdge(u,v,w);
		addEdge(v,u,w);
	}
	Dijkstra(-1,-1);
	for(int i=n;i!=1;i=node[i].prev){
		Dijkstra(i,node[i].prev);
		ans=min(ans,node[n].dis);
	}
	if(ans>=INF)puts("-1");
	else printf("%.2lf\n",ans);
}