目录
前言
一、打家劫舍 ——>房子是线性的
1.1、dp定义
1.2、递推公式
1.3、初始化
1.4、遍历顺序
1.5、解题代码
二、打家劫舍II ——>房子是环型
2.1、分析
2.2、解题代码
三、打家劫舍III ——>房子是树形
3.1、dp含义
3.2、递推公式
3.3、解题代码
小结
前言
本篇题目虽然可以使用其他方法,如暴力枚举、贪心来解,但是只是针对特定场景的问题才可以,所以这里我将用动态规划的方法来教你,怎么偷,才能偷到最多钱~
一、打家劫舍 ——>房子是线性的
题目描述:

题目来源:198. 打家劫舍
1.1、dp定义
分析:
我们需要考虑到每一个房间,并且得出可以偷盗的最大金额,因此dp数组的数值就是我们能偷到的最大金额,就对应第几天~
dp定义:
dp[i]:考虑偷第i个房间(包括之前的房间),可以偷盗的最大金额。
1.2、递推公式
分析:
dp[i]有几种状态?从哪些状态可以推出dp[i]?
一个房间无非就是两种状态,偷或者不偷,根据题目描述,不能连续偷盗两个相邻的房间,所以,当前这个房间如果我们不去偷他,那么当前所拥有的最大金额就是前一个状态dp[i - 1]这个时候所拥有的最大金额,如果要偷,那么前一天一定不能偷,那么当前所拥有的最大金额就是dp[i - 2] + nums[i],也就是不考虑昨天,加上今天一定偷所能获得的最大金额。
递推公式:
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
1.3、初始化
分析:
从递推公式中可以看出需要用到两个状态,dp[i - 1]和dp[i - 2],将这两个状态一直推下去,就可以知道我们需要初始化的是dp[0]和dp[1];
dp[0]表示考虑偷第1个房间,那么现在总共就一个房间,肯定是要偷的。
dp[1]表示考虑偷第2个房间(包括之前的房间),那么现在总共就两个房间,由于不能连续偷相邻房间,因此就偷这两个房间价值最大的。
初始化:
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
1.4、遍历顺序
由递推公式可以知道,要推出当前dp[i],需要知道前两天的状态,所有从左往右遍历即可。
1.5、解题代码
class Solution {
public int rob(int[] nums) {
int len = nums.length;
if(len == 1) return nums[0];
if(len == 2) return Math.max(nums[0], nums[1]);
int[] dp = new int[len];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for(int i = 2; i < len; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[len - 1];
}
}二、打家劫舍II ——>房子是环型
题目描述:

题目来源: 213. 打家劫舍 II
2.1、分析
思考:
虽然房子是一个环型,无非就是要多考虑一个问题,因为不能连续偷盗两个相邻的房间,所以第一个房间和最后一个房间只能偷一个,那么我们可以把它想象成两个线性的结构,如下图:
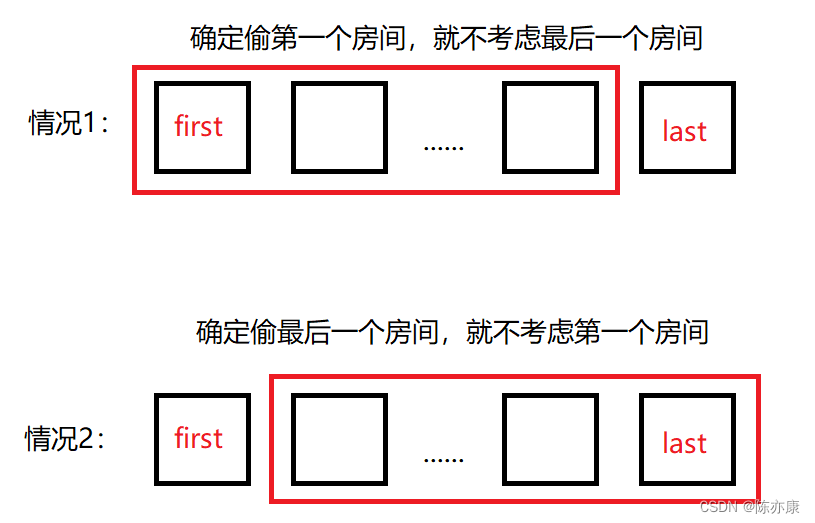
本题与“打家劫舍”这道题一样,最后问的都是所能偷盗的最大价值,因此就可以把题目所给的房间截取成上图中的两端,然后分别用“打家劫舍”那道题的方式进行处理,最后比较出 “偷第一个不偷最后一个” 和 “不偷第一个偷最后一个” 的最大值,就是我们要求的最大价值。
2.2、解题代码
class Solution {
public int rob(int[] nums) {
int len = nums.length;
if(len == 1) return nums[0];
if(len == 2) return Math.max(nums[0], nums[1]);
int first = robI(Arrays.copyOfRange(nums, 0, len - 1));
int last = robI(Arrays.copyOfRange(nums, 1, len));
return Math.max(first, last);
}
private int robI(int[] nums) {
int len = nums.length;
if(len == 1) return nums[0];
if(len == 2) return Math.max(nums[0], nums[1]);
int[] dp = new int[len];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for(int i = 2; i < len; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[len - 1];
}
}三、打家劫舍III ——>房子是树形
题目描述:
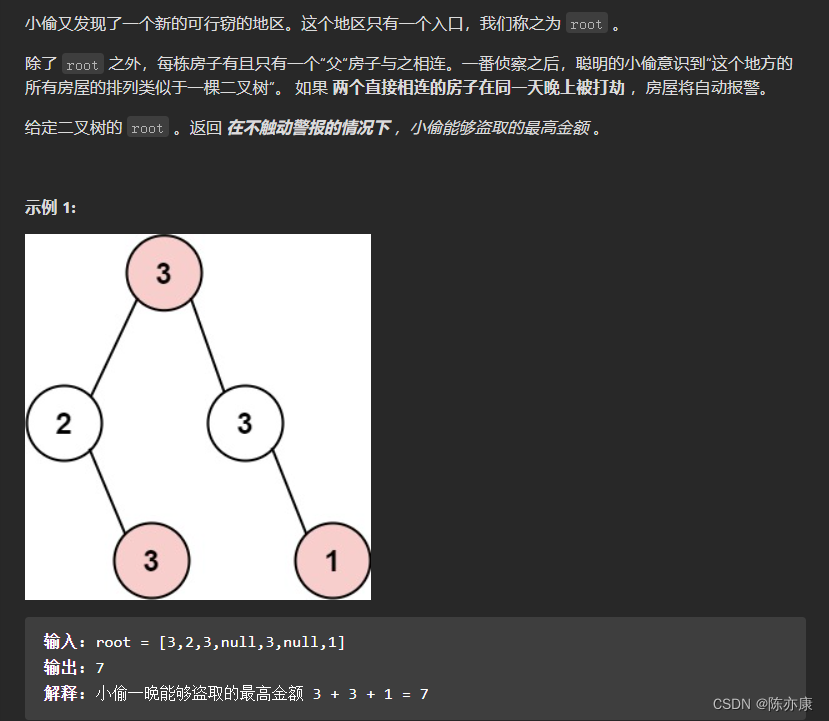
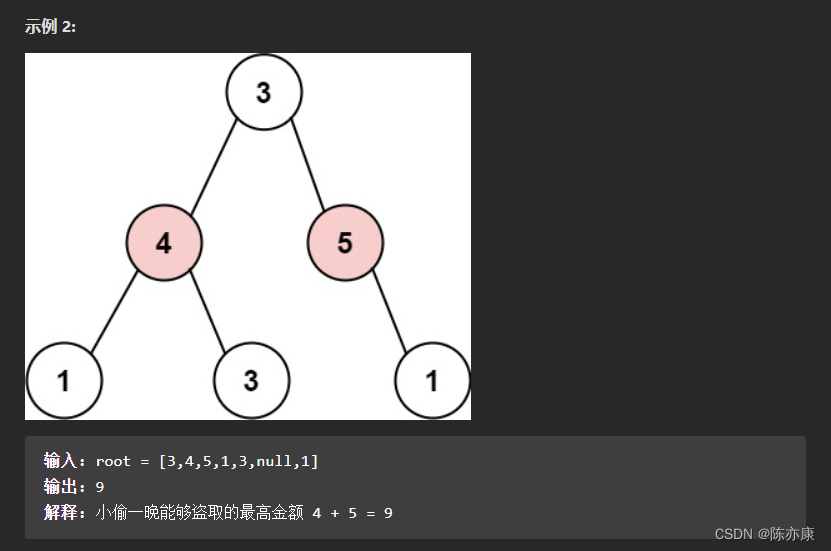
题目来源:337. 打家劫舍 III
3.1、dp含义
分析:
房子是一个树形,我们可以采取一个后续遍历的方式(后面会讲原因),去遍历这颗树,最后得出最大值;
房子只有两种状态,偷或者不偷,我们可以用Pair键值对的形式来保存这两种状态,我们只需要在后序遍历的过程中写下Pair,那么每一个结点都有一个Pair这两种状态,因此可以延续。
初始化:
Pair<Integer, Integer> dp :表示当前房屋偷(getValue())和不偷(getKey())两种最大价值。
最后返回两者最大值即可。
3.2、递推公式
分析:
房子只有偷和不偷两种状态,那么
1.如果偷当前房子,就一定不可以偷当前结点的两个子节点,因此偷当钱房屋的最大价值就是,不偷两个子节点的最大价值(使用后续遍历的原因:这里的子节点的值从何而来,就是需要后序遍历先得到值,现在才能用子节点的返回值) + 当前结点的价值 ——> dpLeft.getKey() + dpRight.getKey() + root.val;
2.如果不偷当前房子,那么两个子节点可以偷也可以选择不偷(比如就拿其中一个子节点来说,这一个子节点可以偷也可以不偷,需要从这两种状态种选出一个最大值),分别得出一个最大值即可,然后求和就是当前所拥有的最大价值 ——>Math.max(dpLeft.getKey(), dpLeft.getValue()) + Math.max(dpRight.getValue(), dpRight.getKey());
动态转移方程:
int val1 = Math.max(dpLeft.getKey(), dpLeft.getValue()) +
Math.max(dpRight.getValue(), dpRight.getKey());//不偷当前结点
int val2 = dpLeft.getKey() + dpRight.getKey() + root.val;//偷当前结点
3.3、解题代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int rob(TreeNode root) {
Pair<Integer, Integer> dp = dfs(root);
return Math.max(dp.getKey(), dp.getValue());
}
private Pair<Integer, Integer> dfs(TreeNode root) {
if(root == null) {
return new Pair<>(0, 0);
}
Pair<Integer, Integer> dpLeft = dfs(root.left);
Pair<Integer, Integer> dpRight = dfs(root.right);
int val1 = Math.max(dpLeft.getKey(), dpLeft.getValue()) +
Math.max(dpRight.getValue(), dpRight.getKey());//不偷
int val2 = dpLeft.getKey() + dpRight.getKey() + root.val;
return new Pair<>(val1, val2);
}
}小结
小偷这么聪明,为啥还要来偷?