象棋中的马跳步问题

作者：Grey

原文地址：

博客园：象棋中的马跳步问题

CSDN：象棋中的马跳步问题

题目描述

中国象棋中，整个棋盘就是横坐标上 9 条线、纵坐标上 10 条线的一个区域，给你三个参数 x，y，k；返回『马』从 (0,0) 位置出发，必须走 k 步；

最后落在 (x,y) 上的方法数有多少种?

题目链接见：牛客-象棋中马的跳法

暴力解法

定义递归函数

int ways(int i, int j, int a, int b, int step)

递归含义表示：从 (i,j) 出发，到 (a,b) 且必须要走 step 步的情况下，有多少种走法。

接下来是 base case，首先 (i,j) 坐标如果已经越界，说明不可能有有效走法，直接返回 -1。

(i, j) 越界的条件是

(i >= 10 || j >= 9 || i < 0 || j < 0)

如果 step == 0，说明没有可走的步数了，此时，除非 (i == a && j == b) ，可以有一种走法（在原地不动），其他情况，都无路可走，返回 -1。

base case 代码如下

        // 象棋区域 int[][] area = new int[10][9]
        if (i >= 10 || j >= 9 || i < 0 || j < 0) {
            // 越界
            return -1;
        }
        if (step == 0) {
            if (i == a && j == b) {
                return 1;
            }
            return -1;
        }

接下来就是普遍情况，『马』可以四面八方尝试

    // 四面八方尝试
        int p1 = ways(i - 2, j + 1, a, b, step - 1);
        int p2 = ways(i - 1, j + 2, a, b, step - 1);
        int p3 = ways(i - 1, j - 2, a, b, step - 1);
        int p4 = ways(i - 2, j - 1, a, b, step - 1);
        int p5 = ways(i + 2, j + 1, a, b, step - 1);
        int p6 = ways(i + 1, j + 2, a, b, step - 1);
        int p7 = ways(i + 1, j - 2, a, b, step - 1);
        int p8 = ways(i + 2, j - 1, a, b, step - 1);

返回这些情况的合计即可。

暴力解法完整代码如下

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int x = in.nextInt();
        int y = in.nextInt();
        int k = in.nextInt();
        System.out.println(ways(0,0,x, y, k));
        in.close();
    }

    // 递归含义：还剩下step步，从(i,j)到达(a，b)可以选择的方法数是多少
    public static int ways(int i, int j, int a, int b, int step) {
        // 象棋区域 int[][] area = new int[10][9]
        if (i >= 10 || j >= 9 || i < 0 || j < 0) {
            // 越界
            return -1;
        }
        if (step == 0) {
            if (i == a && j == b) {
                return 1;
            }
            return -1;
        }
        // 四面八方尝试
        int p1 = ways(i - 2, j + 1, a, b, step - 1);
        int p2 = ways(i - 1, j + 2, a, b, step - 1);
        int p3 = ways(i - 1, j - 2, a, b, step - 1);
        int p4 = ways(i - 2, j - 1, a, b, step - 1);
        int p5 = ways(i + 2, j + 1, a, b, step - 1);
        int p6 = ways(i + 1, j + 2, a, b, step - 1);
        int p7 = ways(i + 1, j - 2, a, b, step - 1);
        int p8 = ways(i + 2, j - 1, a, b, step - 1);
        return ((p1 == -1) ? 0 : p1) + ((p2 == -1) ? 0 : p2) + ((p3 == -1) ? 0 : p3) + ((p4 == -1) ? 0 : p4) + ((p5 == -1) ? 0 : p5) + ((p6 == -1) ? 0 : p6) + ((p7 == -1) ? 0 : p7) + ((p8 == -1) ? 0 : p8);
    }
}

运行超时

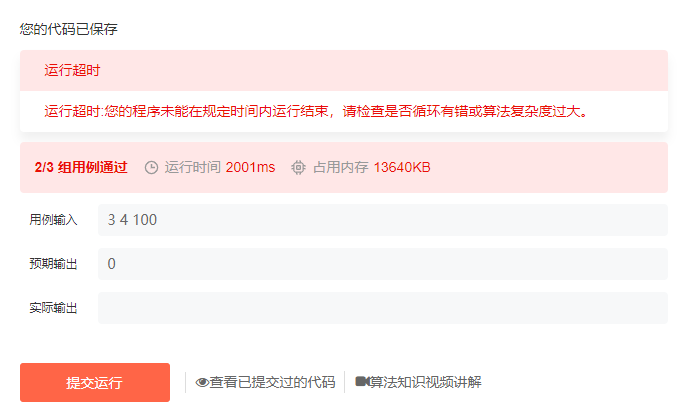
动态规划解（可 AC）

根据上述暴力递归过程可知，递归函数有三个可变参数，分别是 a，b，step，每个参数都有一定的范围，所以可以利用一个三维数组 dp 来囊括所有的递归过程的中间结果。

        // 象棋区域 int[][] area = new int[10][9]
        int[][][] dp = new int[10][9][step + 1];

其中dp[x][y][k]就表示递归函数ways(0,0,x,y,k)的结果。

基于暴力递归的 base case 可知

dp[a][b][0] = 1;

针对普遍情况，暴力递归过程的伪代码如下

    public static int ways(int i, int j, int a, int b, int step) {
        ……
        // 四面八方尝试
        int p1 = ways(i - 2, j + 1, a, b, step - 1);
        int p2 = ways(i - 1, j + 2, a, b, step - 1);
        int p3 = ways(i - 1, j - 2, a, b, step - 1);
        int p4 = ways(i - 2, j - 1, a, b, step - 1);
        int p5 = ways(i + 2, j + 1, a, b, step - 1);
        int p6 = ways(i + 1, j + 2, a, b, step - 1);
        int p7 = ways(i + 1, j - 2, a, b, step - 1);
        int p8 = ways(i + 2, j - 1, a, b, step - 1);
        ……
    }

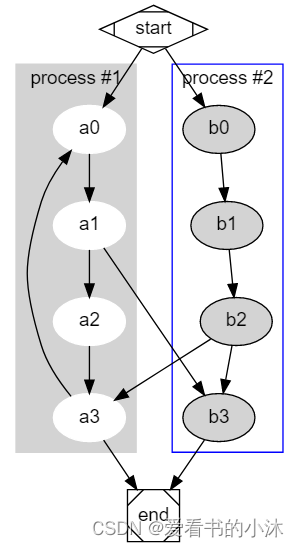
即 dp[i][j][step] 依赖 dp[i-2][j+1][step-1] ， dp[i-1][j+2][step-1] ，dp[i-1][j-2][step-1] ， dp[i-2][j-1][step-1] ，dp[i+2][j+1][step-1] ， dp[i+1][j+2][step-1] ，dp[i+1][j-2][step-1] ， dp[i+2][j-1][step-1] ，示例图如下

如下图，其中(i,j,step)坐标上的点只依赖 step - 1 层上对应的八个点，而不依赖本层任意一点。

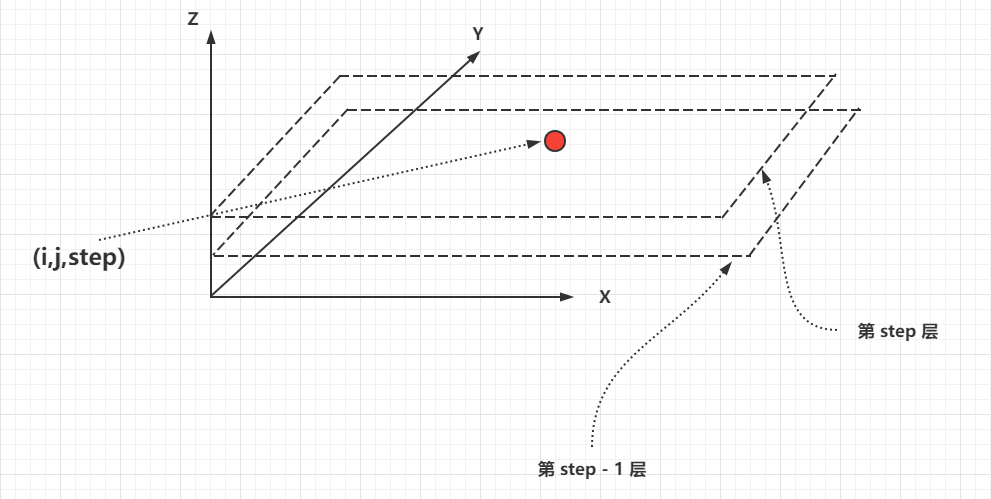
已知第 0 层已经填好了（上面已经提到 dp[a][b][0] = 1 ），所以，可以从 1 层开始，依次填好每一层。

动态规划解完整代码如下


import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int x = in.nextInt();
        int y = in.nextInt();
        int k = in.nextInt();
        System.out.println(ways(x, y, k));
        in.close();
    }

    // 根据暴力递归改动态规划
    public static int ways(int a, int b, int step) {
        // 象棋区域 int[][] area = new int[10][9]
        int[][][] dp = new int[10][9][step + 1];
        dp[a][b][0] = 1;
        for (int k = 0; k < step + 1; k++) {
            for (int i = 0; i < 10; i++) {
                for (int j = 0; j < 9; j++) {
                    if (k == 0) {
                        if (i == a && j == b) {
                            dp[i][j][k] = 1;
                        } else {
                            dp[i][j][k] = -1;
                        }
                    } else {
                        int p1 = (i - 2 >= 0 && j + 1 < 9) ? dp[i - 2][j + 1][k - 1] : -1;
                        int p2 = (i - 1 >= 0 && j + 2 < 9) ? dp[i - 1][j + 2][k - 1] : -1;
                        int p3 = (i - 1 >= 0 && j - 2 >= 0) ? dp[i - 1][j - 2][k - 1] : -1;
                        int p4 = (i - 2 >= 0 && j - 1 >= 0) ? dp[i - 2][j - 1][k - 1] : -1;
                        int p5 = (i + 2 < 10 && j + 1 < 9) ? dp[i + 2][j + 1][k - 1] : -1;
                        int p6 = (i + 1 < 10 && j + 2 < 9) ? dp[i + 1][j + 2][k - 1] : -1;
                        int p7 = (i + 1 < 10 && j - 2 >= 0) ? dp[i + 1][j - 2][k - 1] : -1;
                        int p8 = (i + 2 < 10 && j - 1 >= 0) ? dp[i + 2][j - 1][k - 1] : -1;
                        dp[i][j][k] = (p1 == -1 ? 0 : p1) + (p2 == -1 ? 0 : p2) + (p3 == -1 ? 0 : p3) + (p4 == -1 ? 0 : p4) + (p5 == -1 ? 0 : p5) + (p6 == -1 ? 0 : p6) + (p7 == -1 ? 0 : p7) + (p8 == -1 ? 0 : p8);
                    }
                }
            }
        }
        return dp[0][0][step];
    }

}