一、背景阐述
房地产行业对于国民经济和社会及居民的发展和生活具有很大的影响,而房价能够体现经济运转的好坏,因而房价的波动牵动着开发商和购房者的关注,城市房价预测是一个研究的热点问题,研究房价对民生问题具有重要意义。
本文首先介绍了房地产行业及房价的背景 ,并整理了国内外的相关文献。接着,收集了武汉市2016年1月到2022年5月的房价月度数据,从其时序图可以看出,在疫情影响下,2019年底武汉市房价大幅下降,此后到2021年年底,一直是波动的趋势,2022年开始呈现出下降的趋势。然后,对收集到的数据进行平稳性检验,再进行差分处理,使之成为平稳的随机序列,在此基础上继续对数据进行白噪声检验和ADF检验,最后对观察数据拟合ARIMA(1,2,2)模型。。。。。
二、文献综述
国外有许多学者研究了房地产行业的问题。Hekman在1979年综合一些经济因素对房价进行了分析,结果表明经济因素对于房价有显著的影响;Clayton研究了基于波动的理性预期对于房地产价格的影响,然而研究结论与理想的结果并不符合;Normanm Liang对美国两百多个城市的房地产销售价格进行了研究,发现经济条件不同其波动规律不同,并且房价的变化速率的时间段不一样也会存在很大差异。。。。
三、实证分析
数据展示如下表,对于部分缺失值,采用平均值替代法。
表1 2016年1月-2022年5月武汉市月度房价 单位:元
数据和代码
报告代码数据
| 2016年 | 2017年 | 2018年 | 2019年 | 2020年 | 2021年 | 2022年 | |
| 1月 | 10001 | 13987 | 16255 | 17814 | 16629 | 16933 | 17141 |
| 2月 | 10001 | 14117 | 16264 | 18581 | 16742 | 16561 | 17068 |
| 3月 | 10224 | 14680 | 16403 | 18554 | 16638 | 16737 | 16751 |
| 4月 | 10478 | 15024 | 16484 | 18253 | 17540 | 16288 | 16699 |
数据的描述性统计如表2所示。
表 2 数据的描述性统计
| Min. | 1stQu. | Median | Mean | 3rdQu. | Max. | |
| price | 10001 | 15779 | 16492 | 15892 | 17141 | 18581 |
序列的时序图、自相关图及单根检验等可以用来检验序列的平稳性。
应用R作2016年1月-2022年5月武汉市房价的时序图如图1所示。
library(forecast)
library(lmtest)
library(zoo)
#__________________________________________________________________________
data<-read.table("C:/Users/dataw.csv",header=TRUE,sep=",")
data
price=data$wuhan
summary(price)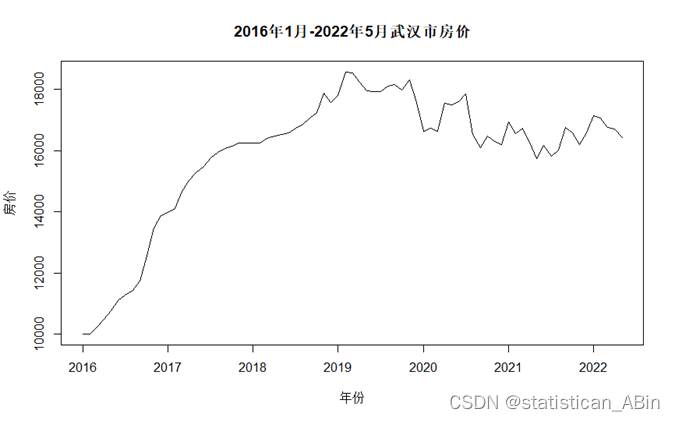
从时序图图1中可以清楚的看到该序列蕴涵曲线增长的长期趋势,为非平稳序列。
接下来进行自相关检验,
#绘制自相关图和偏自相关图
acf(price)
pacf(price)
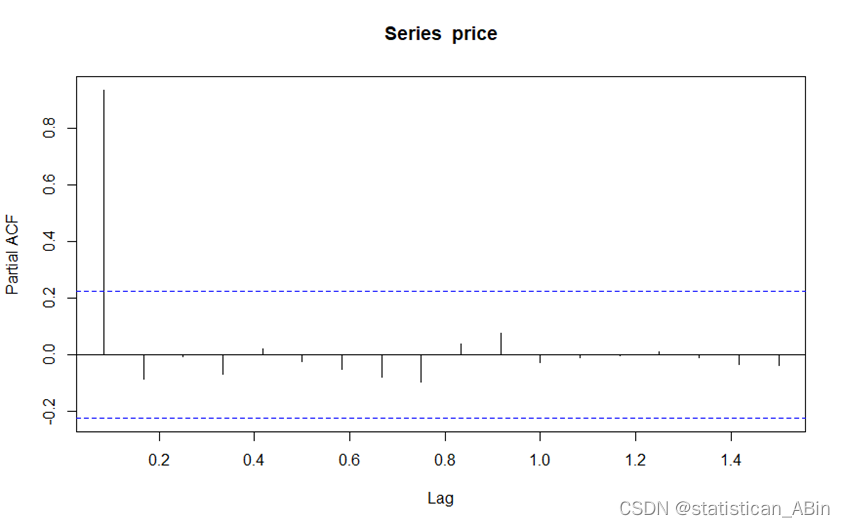
结合时间序列时序图和序列自相关图,可以认为2016年1月到2022年5月武汉市房价序列为非平稳时间序列,不能直接构建ARIMA模型,需要进行差分处理。
#1阶差分,并绘制差分后序列时序图
price.dif<-diff(price)
plot(price.dif)

对二阶差分后的数据进行ADF平稳性检验,结果如表3所示。
表 3 延迟2期平稳性检验
adf.test(price.dif,3)| 检验形式 | no drift no trend | with drift no trend | with drift and trend | |
| Price | ADF统计量 | -6.78 | -6.74 | -6.69 |
| 对应P值 | 0.01 | 0.01 | 0.01 |
从表3看出,在0.05的显著性水平下,二阶差分单位根检验值 P 等于0.01且小于0.05,说明二阶差分后的序列已经趋于平稳。
按照上面自相关图和偏自相关图的内容,以及对武汉市房价数据序列进行了二次差分,并结合自动定阶的函数,计算得到模型应该采用ARIMA(1,2,2)
#自动定阶
auto.arima(price.dif2)
#模型拟合
price.fit<-arima(price,order=c(1,2,2))
price.fit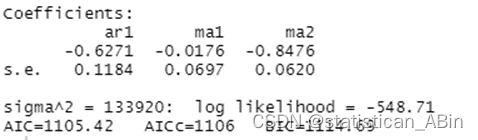
的ARIMA模型表达式如下
![]()
对拟合的模型进行白噪声检验,结果如表5所示。
表 5白噪声检验
| 滞后期数 | 卡方统计量 | P值 | |
| Price | 滞后6期P值 | 4.5465 | 0.6031 |
| 滞后12期P值 | 13.251 | 0.3511 |
从表5可以看到在0.05的显著性水平下,price数据在滞后6和12期都接受原假设,残差均是白噪声。。。。
最后利用ARIMA(1,2,2)模型对武汉市的房价进行预测,预测6期,即未来六个月房价数据,
#模型预测
price.fore<-forecast(price.fit,h=6)
price.fore
plot(price.fore)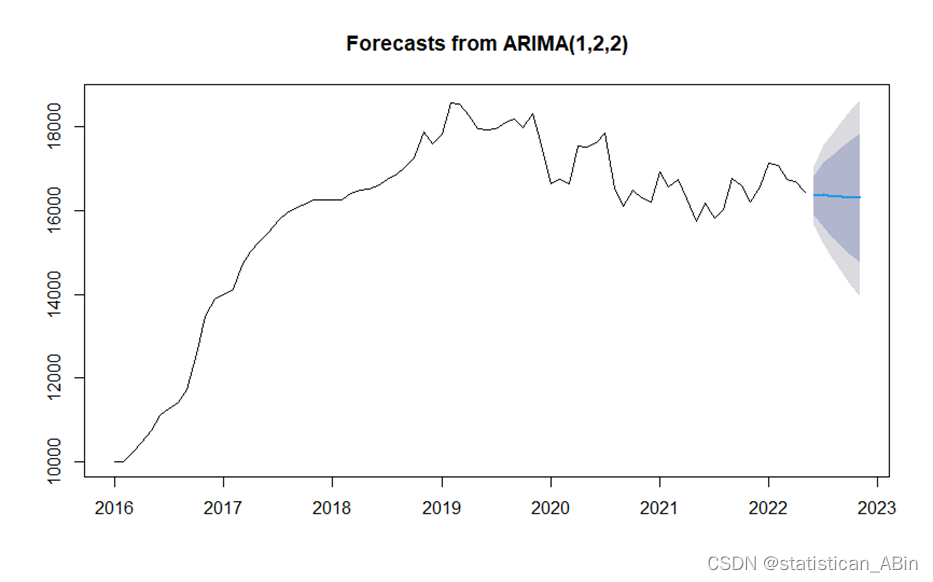
从图中可以看到武汉市房价在2022年5月后的六个月呈现出较为平稳的趋势。
四、总结
在疫情影响下,2019年底武汉市房价大幅下降,此后到2021年年底,一直是波动的趋势,2022年开始呈现出下降的趋势。利用ARIMA模型进行预测,武汉市房价在2022年5月后会呈现出较为平稳的趋势。而三次平滑法预测结果显示,武汉市房价在2022年5月后会先下降后上涨,有波动趋势。这。。。
参考文献
[1] Pollakowski.H.0,S.M.Wachter. The Effect of Land-Use Constraints on Housing Prices[J].
LandEconomics,1990,66(3):315-324.
[2] Norman Miller Liang Peng.Exploring metropolitan housing price volatility [J].Real Estate
Econ.2016.
[3]吴承业,沈逸珺,汪慰,等.基于 ARMA 模型的杭州市房价研究与预测———以杭州市上城区和下城区为例[J].湖州师范学院学 报,2020,42(8):19-26+33.
创作不易,希望大家多点赞关注评论!!!(类似代码或报告定制可以私信)