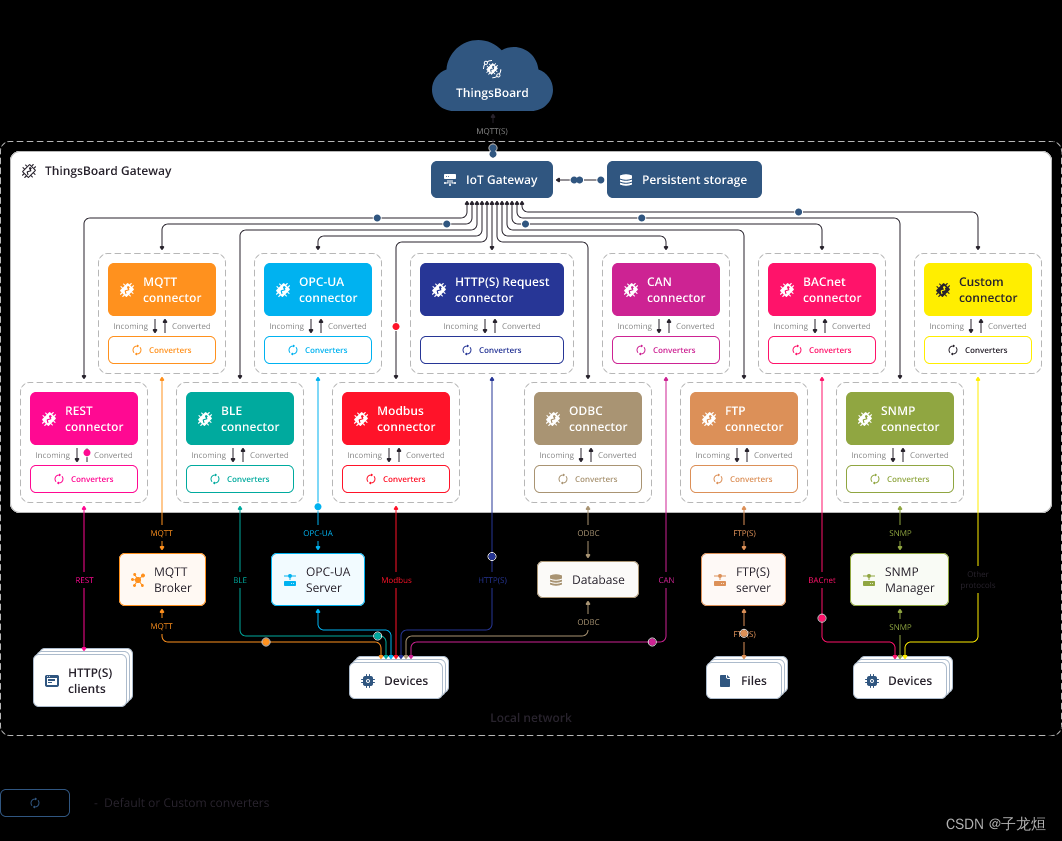
一、错位相减法

设，a_n是等差数列，b_n是等比数列，那么{a_n*b_n}构成一个新的数列
这个新数列的求和公式，就可以用错位相减法求解。

练习

例题1

解析：
第一问

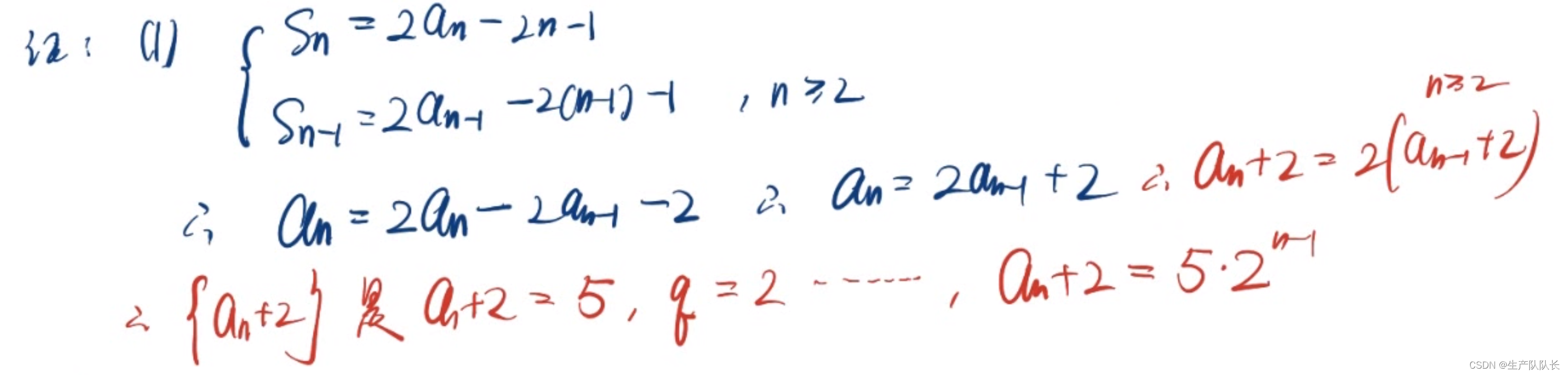
第二问

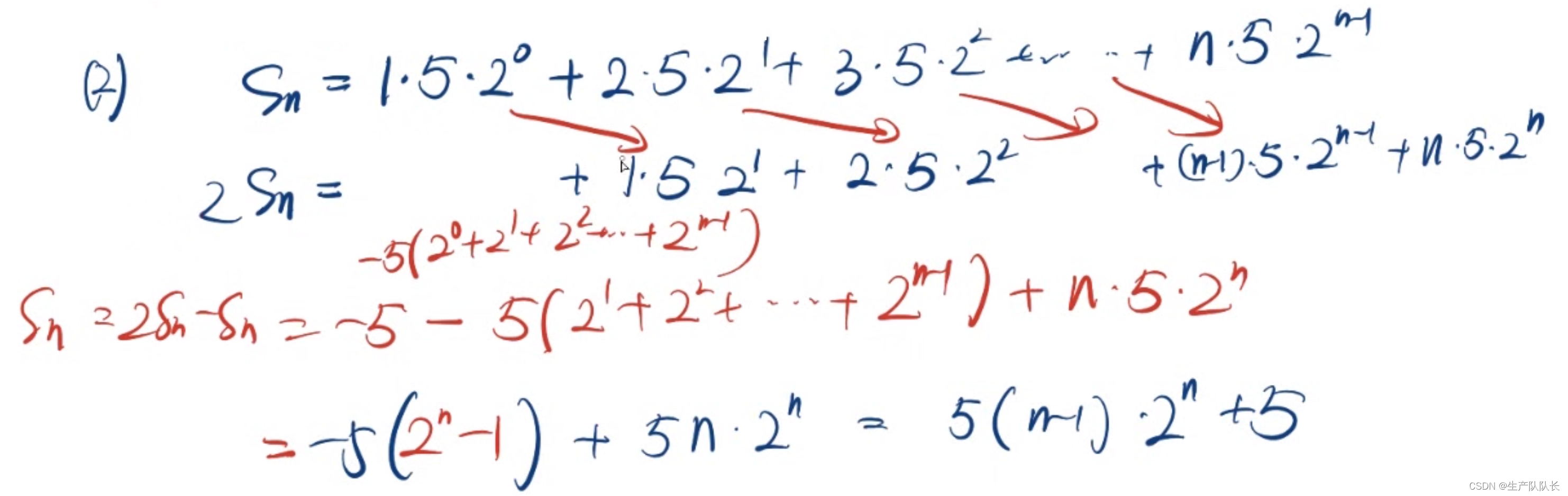
二、裂项相消法

1、裂项的几种常见形式

形式1

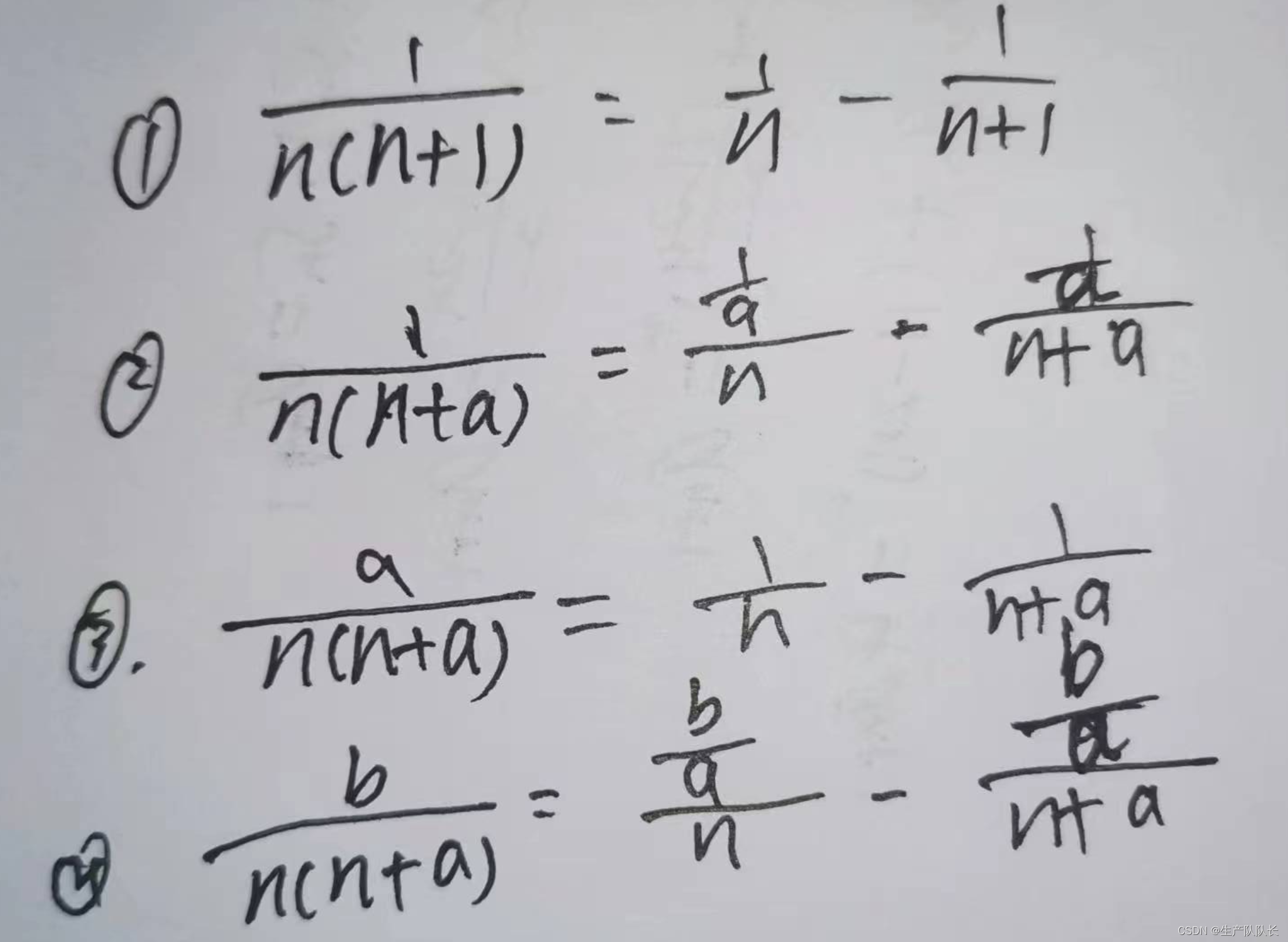
注意：其实这里的一般形式，应该含有4个常数，至于证明方法，其实差不多。
高中主要处理的情况都是，n前的系数相等，这样裂开后只剩下常数。
所以，这里只考虑2个参数的情况。
那么，以后我们遇到更一般的式子，怎么裂开了？
方法就是：先直接裂开，分子设为1，在计算分子，差多少补多少

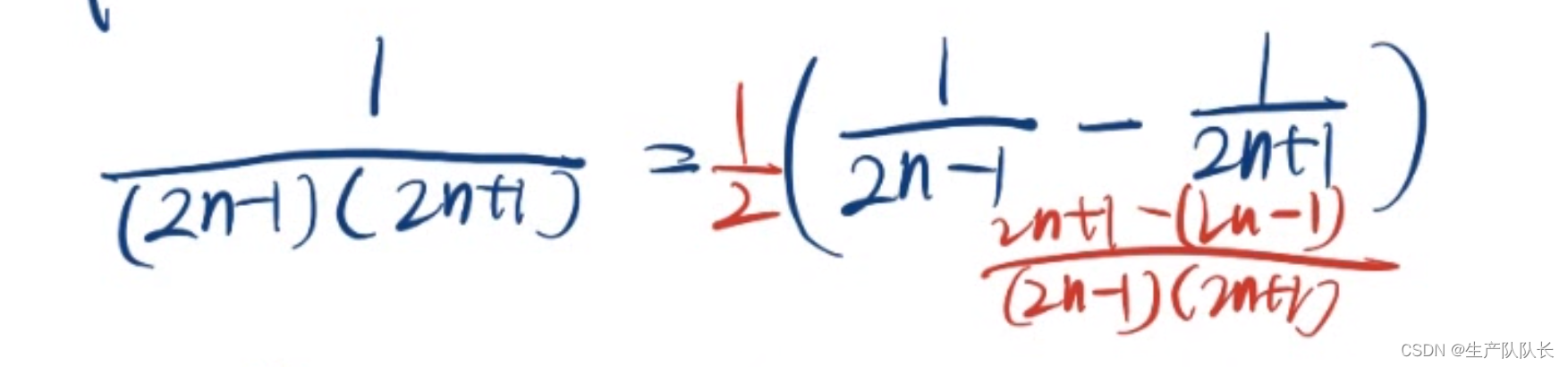
形式2

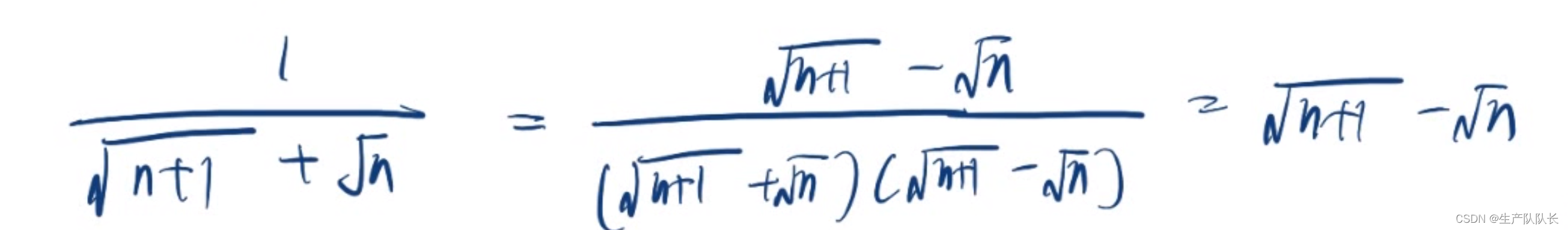
形式3
分母是连续三项乘积

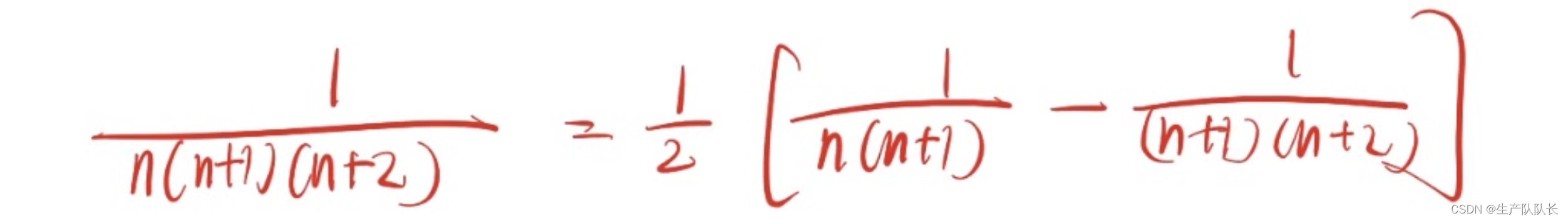
2、裂项后，再求和

例1

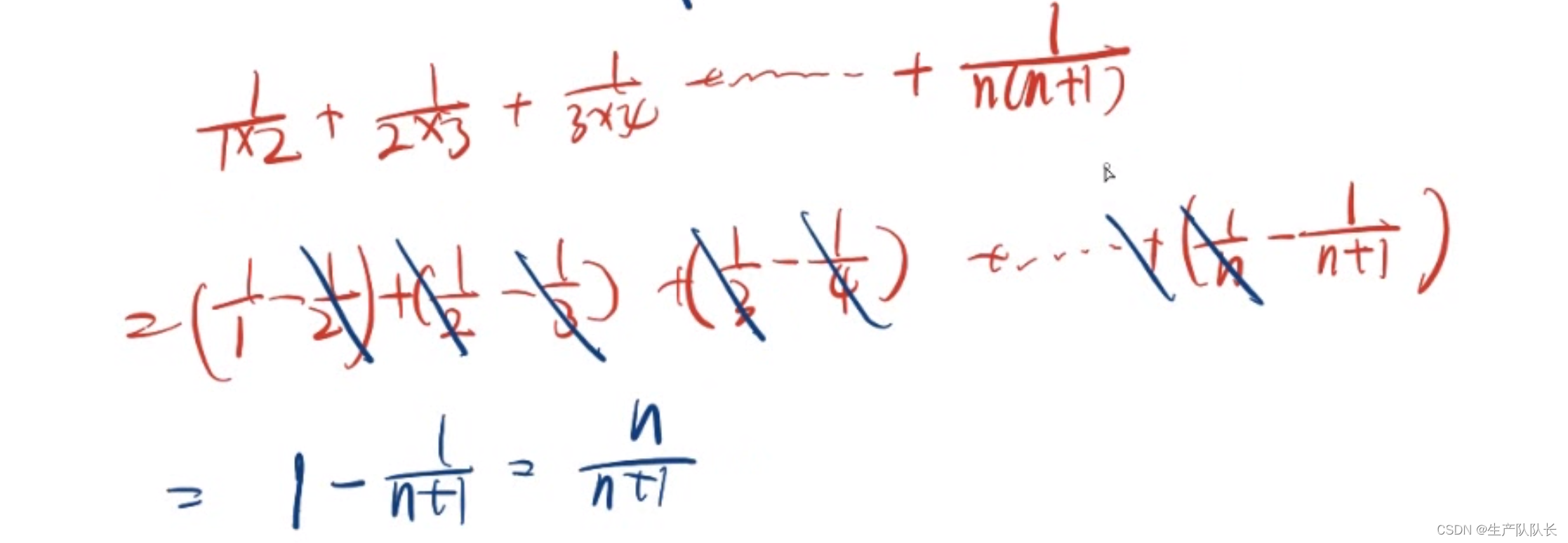
例2

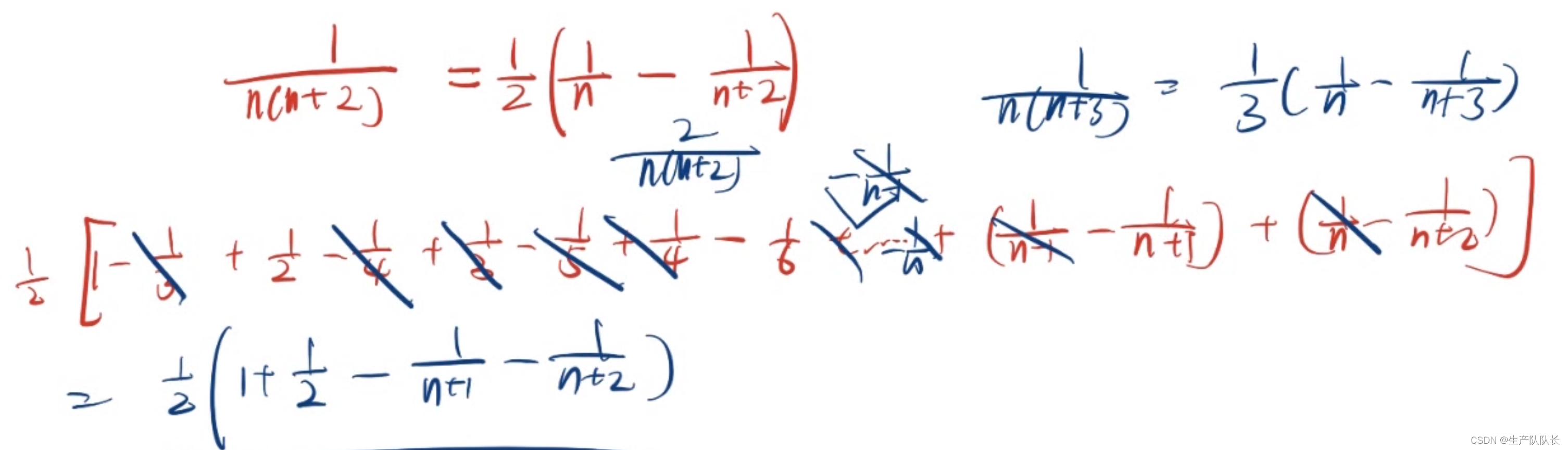
3、练习

例题1

解析：
第一问
这里，有个小难点，在于，如何验证n=1的时候，a_n也成立。
验证思路是这样的
1、根据已知条件，代入n=1，求出a₁
2、根据通项公式a_n，求出a₁
3、比较，根据条件得出的a₁和通项公式得出的a₁是否相等。如果相等，则可以取到1
如果不相等，则是分段表示。

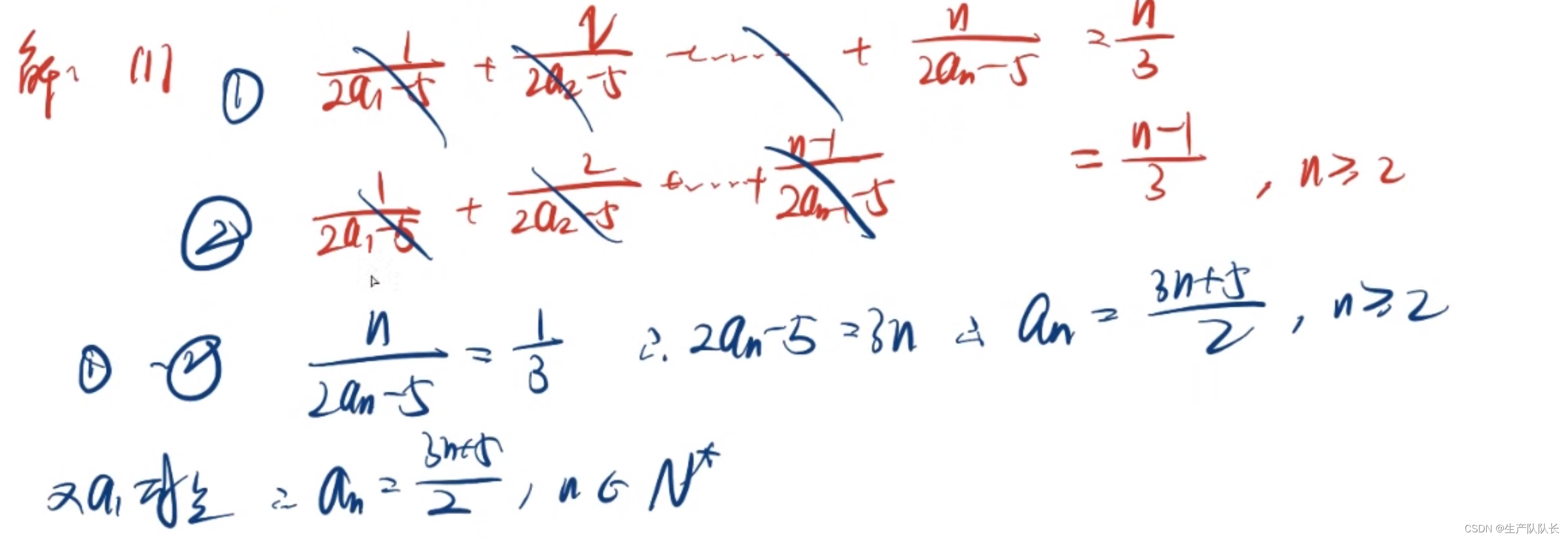
第二问
通项公式求出来后，第二问就直接用裂项相加法秒杀。