第一题：

原题链接：513. 找树左下角的值 - 力扣（LeetCode）

思路：用回溯的思想：

这题就是求最大深度，当遍历到第一个最大深度的时候，记录下的节点值就是最左边的元素。

参数和返回值：参数需要有一个来记录此时的节点的深度，传入下一层递归的时候进行比较，同时这个参数也是要进行回溯的，当回溯的时候深度就要-1；

终止条件：当左右节点都为空的时候同时当前深度大于最大的深度，将该节点的值记录同时更新最大深度。

单层递归逻辑：向左子树遍历的时候depth++，递归完后要depth--进行回溯。右子树同理；

代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        dfs(root, 0);
        return res;
    }
private:
    int res;
    int maxdepth = INT_MIN;
    void dfs(TreeNode* root, int depth){
        if(root -> left == nullptr && root -> right == nullptr){
            if(depth > maxdepth){
                maxdepth = depth;
                res = root -> val;
            }
            return;
        }
        if(root -> left){
            depth++;
            dfs(root -> left, depth);
            depth--;
        }
        if(root -> right){
            depth++;
            dfs(root -> right, depth);
            depth--;
        }
    }
};

第二题：

原题链接：112. 路径总和 - 力扣（LeetCode）

思路：

终止条件：当前遍历的节点的左右节点都为空并且节点的值等于targetSum的值则返回true；

单层递归逻辑：采用后序遍历的方式，左右中。

用bool left 和 right分别接住左右子树是否为true；

最后返回left || right.

代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == nullptr) return false;
        if(root -> left == nullptr && root -> right == nullptr && root -> val == targetSum){
            return true;
        }
        bool Bleft = hasPathSum(root -> left, targetSum - root -> val);
        bool Bright = hasPathSum(root -> right, targetSum - root -> val);
        return Bleft || Bright;
    }
};

第三题：

原题链接：113. 路径总和 II - 力扣（LeetCode）

思路：

参数和返回值:就是题目的那个。

终止条件：当前遍历的节点的左右节点都为空并且当前节点的值等于targetSum的值，则将该这条路径添加到res数组中。

单层递归逻辑：

采用中序遍历的方式，中左右，中间节点先添加到路径，向左遍历的时候targetSum的值-=节点的值传递给下一层递归逻辑。然后回溯，将减去的值重新加到targetSum中，同时加入路径中的节点值也要弹出。同理向右子树遍历。

代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        if(root == nullptr) return {};
        dfs(root, targetSum);
        return res;
    }
private:
    vector<int> path;
    vector<vector<int>> res;
    void dfs(TreeNode* root, int targetSum){
        path.push_back(root -> val);
        if(root -> left == nullptr && root -> right == nullptr && root ->val == targetSum){
            res.push_back(path);
        }
        if(root -> left){
            dfs(root -> left, targetSum - root -> val);
            path.pop_back();
        }
        if(root -> right){
            dfs(root -> right, targetSum - root -> val);
            path.pop_back();
        }
    }
};

第四题：

原题链接：106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

思路：

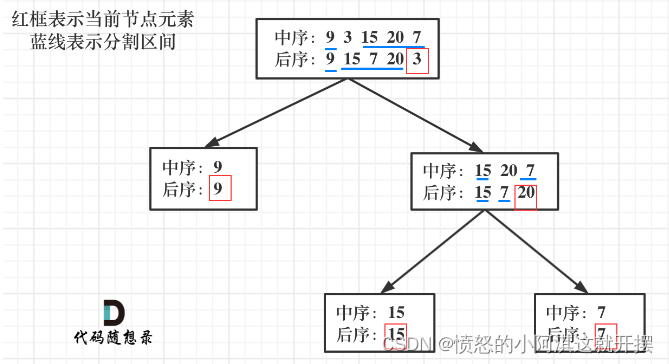
首先找到根节点，就是后序遍历的最后一个元素。

找到在中序遍历中的根节点。

对中序遍历进行切割，分成左右两个子树。

根据中序遍历切割出来的子树的大小对后序遍历的数组进行切割。

最后递归处理中序和后序的左右区间。

代码如下：

class Solution {
private:
    TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
        if (postorder.size() == 0) return NULL;

        // 后序遍历数组最后一个元素，就是当前的中间节点
        int rootValue = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootValue);

        // 叶子节点
        if (postorder.size() == 1) return root;

        // 找到中序遍历的切割点
        int delimiterIndex;
        for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }

        // 切割中序数组
        // 左闭右开区间：[0, delimiterIndex)
        vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
        // [delimiterIndex + 1, end)
        vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );

        // postorder 舍弃末尾元素
        postorder.resize(postorder.size() - 1);

        // 切割后序数组
        // 依然左闭右开，注意这里使用了左中序数组大小作为切割点
        // [0, leftInorder.size)
        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        // [leftInorder.size(), end)
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

        root->left = traversal(leftInorder, leftPostorder);
        root->right = traversal(rightInorder, rightPostorder);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, postorder);
    }
};