神经网络的编程基础

1. 二分类

二分类是机器学习中的一种基本分类问题，其中每个样本被划分为两个类别中的一个，即正类或负类。这种分类问题在现实生活中有广泛的应用，例如判定邮件是否为垃圾邮件、判别某个人是否患病等。二分类模型根据样本的特征对样本赋予一个标签，这个标签只有两个类别，如0和1，或者正类和负类。

2. 逻辑回归

logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。 逻辑回归根据给定的自变量数据集来估计事件的发生概率，由于结果是一个概率，因此因变量的范围在0和1之间。

3. 逻辑回归的代价函数

逻辑回归的代价函数是用来衡量逻辑回归模型预测值与真实值之间的差距的函数。

4. 梯度下降法

梯度下降法（英语：Gradient descent）是一个一阶最优化算法。要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索，则会接近函数的局部极大值点；这个过程则被称为梯度上升法。

5. 导数

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f’（x0）或df（x0）/dx。

6. 更多导数的例子

第一点，导数就是斜率，而函数的斜率，在不同的点是不同的。在第一个例子中𝑓(𝑎) =3𝑎
，这是一条直线，在任何点它的斜率都是相同的，均为 3。但是对于函数𝑓(𝑎) = a^2 ，或者𝑓(𝑎) =
log𝑎，它们的斜率是变化的，所以它们的导数或者斜率，在曲线上不同的点处是不 同的。
 
第二点，如果你想知道一个函数的导数，你可参考你的微积分课本或者维基百科，然后你应该就能找到这些函数的导数公式。

7. 计算图

计算图（Computation Graph）是一种用于描述数学计算的图形模型，常用于神经网络的前向传播和反向传播算法中。

8. 使用计算图求导数
   

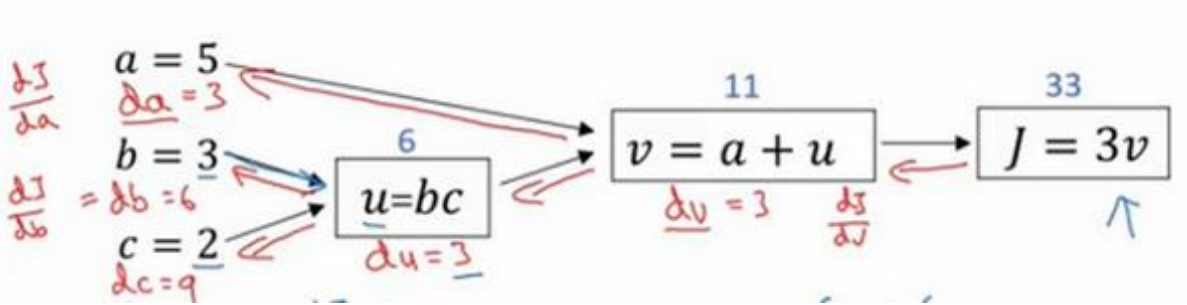
9. 逻辑回归中的梯度下降
   

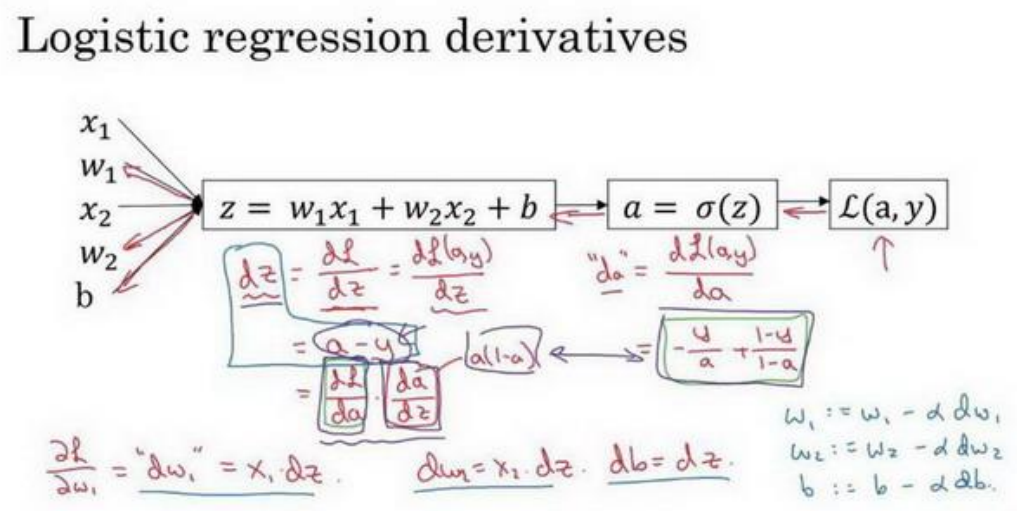
10. m 个样本的梯度下降
    

11. 向量化

当你应用深度学习算法，你会发现在代码中显式地使用 for循环使你的算法很低效，同时在深度学习领域会有越来越大的数据集。所以能够应用你的算法且没有显式的 for循环会是重要的，并且会帮助你适用于更大的数据集。所以这里有一些叫做向量化技术,它可以允许你的代码摆脱这些显式的 for 循环。

12. 向量化的更多例子
    

13. 向量化逻辑回归
    

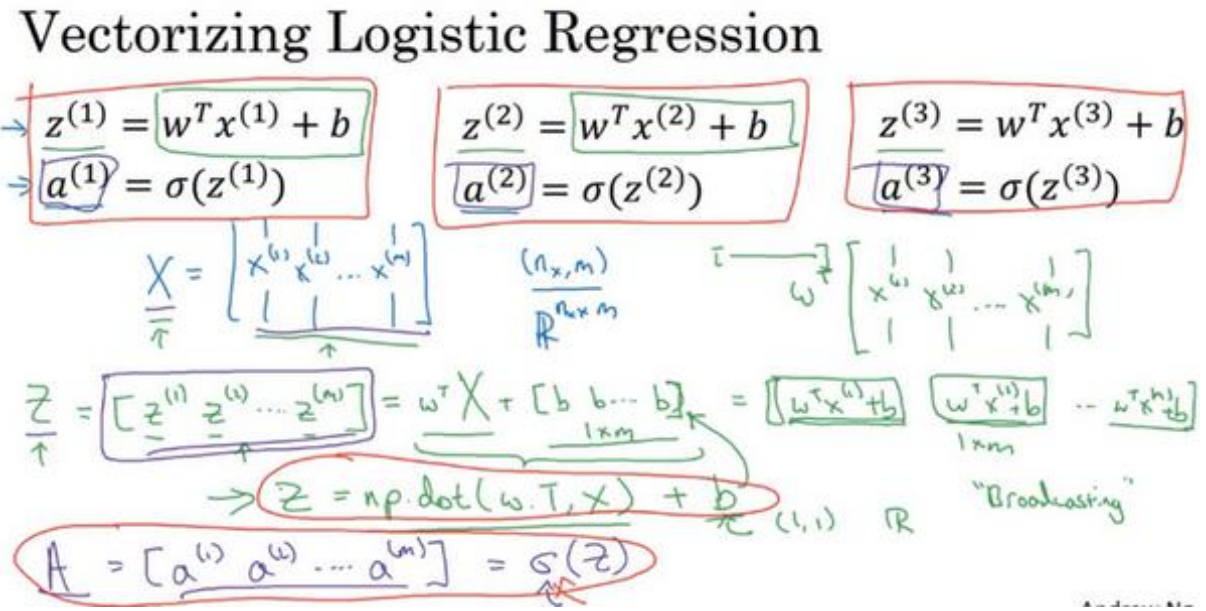
14. 向量化logistic回归的梯度输出
    

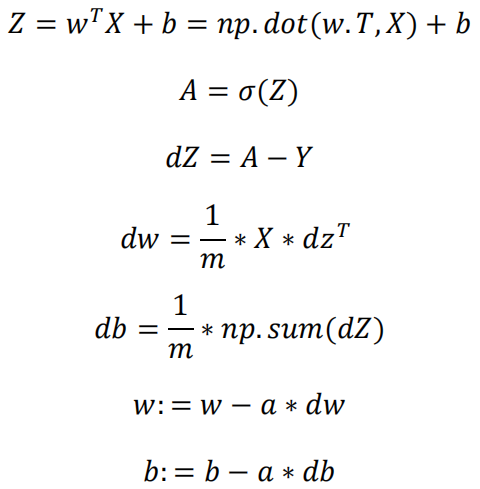
15. python中的广播