文章目录
- 引言
- 复习
- 区间DP——加分二叉树
- 个人实现
- 背包问题——买书
- 个人实现
- 参考实现
- 新作
- 移除元素
- 个人实现
- 参考思路
- 找出字符串中第一个匹配项的下标
- 个人实现
- 参考实现
- 总结
引言
- 今天做了一个噩梦,然后流了一身汗,然后没起来,九点多才起床背书。十点钟才开始把昨天那道题题目过一遍,然后十一点才开始复习题目,为了不耽误下午的时间,所以这里的就单纯做已经做过的题目,主打一个有量,不在学习新的dp。
复习
区间DP——加分二叉树
-
这道题差不多看了第二遍,第一次学的时候就蛮难的,不过有固定的编程范式,不过这里没想起来。提供一下之前的分析思路。
- 第一次分析
- 区间DP——合并石子
-
之前做了两次,这次看看能不能一次过。
个人实现
- 区间DP集合表示是f[i][j],
- i是区间的左端点
- j是区间的右端点,
- 集合划分是区间的中间的,所以需要遍历枚举区间[i,j]中所有的区间分割点
- 具体的代码流程如下
- 列举区间长度
- 列举区间左端点
- 枚举的区间的分割点
实现问题
- 区间长度的上下限有没有特殊情况,需不需要特殊考虑?如果区间长度为1,或者为n怎么办?
- 特殊情况1
- 区间长度为1,表示的左右子节是重合的,所以需要特殊考虑,当前情况是叶子节点
- 区间长度就是1到n,不用考虑n+1,之前那个题目使用n+1是特殊情况,实际情况下,不需要使用使用n+1,而且这道题使用n+1也没有任何意义,那道题股票买卖题n+1一天的某种情况,是之前最大的。
#include <iostream>
using namespace std;
const int N = 35;
int f[N][N],n,rp[N][N]; // f表示区间的状态记录,r表示根节点的记录状态
int s[N];
void dfs(int l,int r){
if (l > r) return ;
int k = rp[l][r];
cout<<k<<" ";
if (k - 1 >= l) dfs(l,k - 1);
if (k + 1 <= r) dfs(k + 1,r);
}
int main(){
cin>>n;
for (int i = 1; i <= n; ++i) {
cin>>s[i];
s[i] += s[i - 1];
}
// 区间DP
for (int len = 1; len <= n; ++len) {
// 列举区间左端点
for (int l = 1; l + len <= n; ++l) {
// 计算区间的右端点
int r = l + len - 1;
// 列举区间的分割点
for (int k = l; k <= r; ++k) {
if(看== 1)
int temp;
if (k == l){
// 左端点为空
temp = (s[k] -s[k - 1]) + f[k + 1][r];
}else if(k == r){
// 右子树为空
temp = (s[k] -s[k - 1]) + f[l][k - 1];
}else{
// 左右子树都不为空
temp = (s[k] -s[k - 1]) + f[k + 1][r] * f[l][k - 1];
}
// 比较确定最大值的并进行记录
if (f[l][r] < temp) {
rp[l][r] = k;
f[l][r] = temp;
}
}
}
}
cout<<f[0][n];
dfs(0,n);
return f[0][n];
}
修改之后的如下
- 其实这里有两个地方还是可以修改的,左右节点的情况是可以特殊讨论和考虑的。
#include <iostream>
using namespace std;
const int N = 35;
int f[N][N],n,rp[N][N]; // f表示区间的状态记录,r表示根节点的记录状态
int s[N];
void dfs(int l,int r){
if (l > r) return ;
int k = rp[l][r];
cout<<k<<" ";
if (k - 1 >= l) dfs(l,k - 1);
if (k + 1 <= r) dfs(k + 1,r);
}
int main(){
cin>>n;
for (int i = 1; i <= n; ++i) {
cin>>s[i];
}
// 区间DP
for (int len = 1; len <= n; ++len) {
// 列举区间左端点
for (int l = 1; l + len <= n; ++l) {
// 计算区间的右端点
int r = l + len - 1;
if (l == r) f[l][r] = s[l],rp[l][r] = l;
else
// 列举区间的分割点
for (int k = l; k <= r; ++k) {
int temp;
if (k == l){
// 左端点为空
temp = s[k] + f[k + 1][r];
}else if(k == r){
// 右子树为空
temp = s[k] + f[l][k - 1];
}else{
// 左右子树都不为空
temp = s[k] + f[k + 1][r] * f[l][k - 1];
}
// 比较确定最大值的并进行记录
if (f[l][r] < temp) {
rp[l][r] = k;
f[l][r] = temp;
}
}
}
}
cout<<f[0][n];
dfs(0,n);
return f[0][n];
}
背包问题——买书
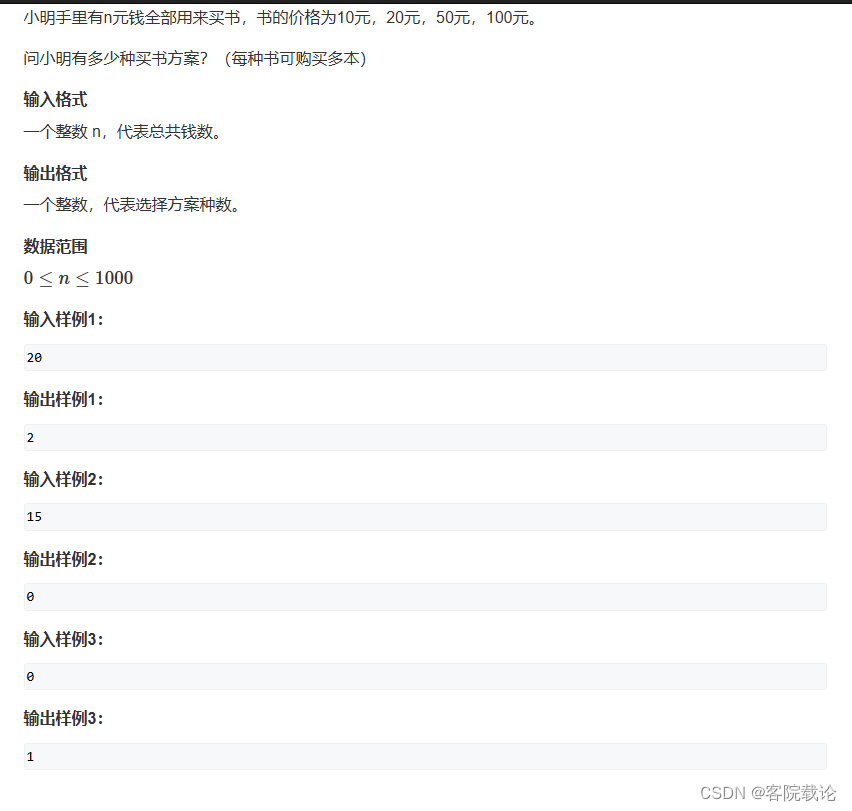
- 标准的背包问题
个人实现
- 标准的背包问题,但是是计算方案数量的,而且会存在重复方案的问题,需要去除重复?是一个问题,并不是那么好去掉重复的。
- 但是如果一开始是按照顺序进行购买的,后续只会增加更贵的物品,我应该如何进行计算?
- 方案数应该怎么计算?直接求,整个矩阵的累加和就行了。
- 注意,这里有一个,所有书全部用来购买书,手里不能有剩钱。
这是一个重复背包问题,属实不会弄,该想想怎么弄了!
#include <iostream>
using namespace std;
const int N = 10010;
int f[N],n;
int w[4] = {10,20,50,100};
int main(){
cin>>n;
int sum = 0;
if (n % 10 != 0) cout<<0<<endl;
else {
for (int i = 0; i < 4; ++i) {
for (int j = n; j >= w[i]; j--) {
f[j] = f[j - w[i]] + f[j];
}
}
cout << sum;
}
}
参考实现
- 参考作者:一只野生彩色铅笔
链接:https://www.acwing.com/solution/content/52967/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
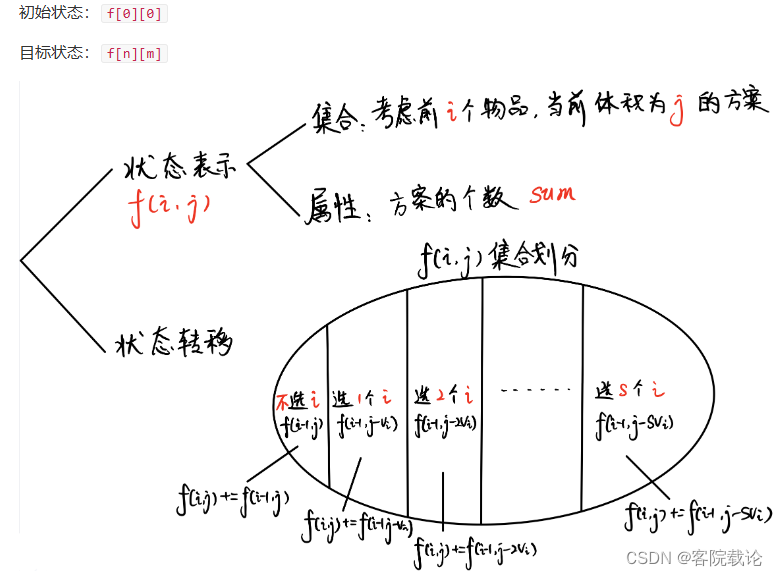
- 下述方法还是很朴素的,确实如此,这道题暂时先跳过,这个方案转换公式是想到了,但是没有写出来。关键是他还有优化,下次再来吧,还要看redis,没那么多时间。
#include <iostream>
using namespace std;
const int N = 5, M = 1010;
int n = 4, m;
int v[N] = {0, 10, 20, 50, 100};
int f[N][M];
int main()
{
//input
cin >> m;
//dp
f[0][0] = 1;
for (int i = 1; i <= n; ++ i)
{
for (int j = 0; j <= m; ++ j)
{
for (int k = 0; v[i] * k <= j; ++ k)
{
f[i][j] += f[i - 1][j - v[i] * k];
}
}
}
//output
cout << f[n][m] << endl;
return 0;
}
新作
移除元素
题目链接


个人实现
重点
- 原地移除所有等于val的元素,后续的元素向前移动
- 保证前k个元素是不等于val的,并且原来的顺序不变
- nums的其余元素和nums的大小并不重要
实现思路
- 两个指针,一个从前往后,一个从后往前
- 从前往后的负责遍历对应的数组,判定当前的元素是否等于val,然后从后往前的元素负责将不相等的元素移动到从前往后的索引下方。
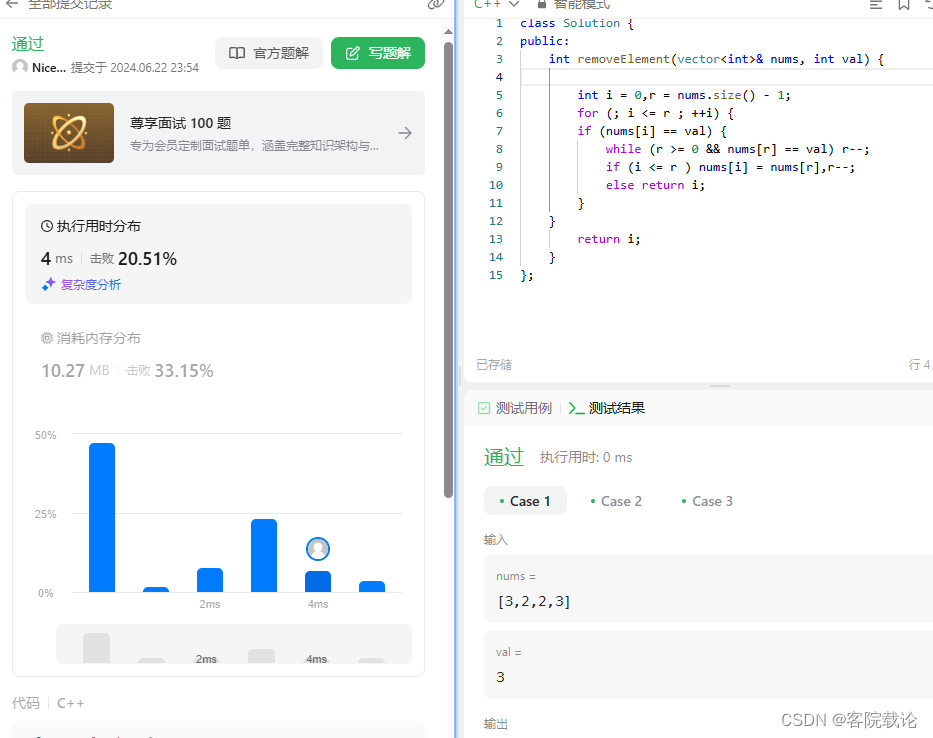
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int i = 0,r = nums.size() - 1;
for (; i <= r ; ++i) {
if (nums[i] == val) {
while (r >= 0 && nums[r] == val) r--;
if (i <= r ) nums[i] = nums[r],r--;
else return i;
}
}
return i;
}
};
总结
- 做是做出来了 ,但是说实话,稀碎,明明是道简单的题目,但是还是调了很久,思路很快就想到了,但是总是遇到各种各样的bug。
- 有以下几个细节需要注意
- 凡是涉及到数组索引的,都要进行检测,防止数组越界。这次在遍历右指针的时候,有好几个地方都没有对指针进行检查,导致不断报错溢出,很难受。
参考思路
-
这个思路太暴力了,时间复杂度比我的高,完整遍历了整个数组。不对,其实我也是遍历了整个数组,不过我是双指针。而且是反向的,不行,这样完全没有必要。
-
就是两个指针
- idx表示实际的指针,只有不同的时候才会赋值并且递增
- i表示遍历的指针,如果不同就执行赋值,如果相同就跳过。
-
老是会把问题想的太复杂!
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int idx = 0;
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] != val){
nums[idx] = nums[i];
idx ++;
}
}
return idx;
}
};
找出字符串中第一个匹配项的下标
- 题目链接

个人实现
重点
- 第一个字符串中找出第二个字符串的第一个匹配项目的下标
- 第二个字符串是一个子串,然后在第一个字符串中找到字串出现的第一个索引位置
思路实现
- 别把这个问题想的太复杂,这是一道简单题,并不是中等题,所以怎么想就怎么实现。
- 最直白的方式,就是两个指针进行遍历
class Solution {
public:
int strStr(string h, string n) {
bool f;
for (int i = 0; i < h.size(); ++i) {
f = true;
for (int j = 0; j < n.size(); ++j) {
if (h[i + j] != n[j]) {
f = false;
break;
}
}
if (f) return i;
}
return -1;
}
};
参考实现
- 跳过吧,这个是用KMP算法的模板题,没有必要!
- 这里仅仅贴一个代码就行了。
class Solution {
public:
int strStr(string s, string p) {
if (p.empty()) return 0;
int n = s.size(), m = p.size();
s = ' ' + s, p = ' ' + p;
vector<int> next(m + 1);
for (int i = 2, j = 0; i <= m; i ++ ) {
while (j && p[i] != p[j + 1]) j = next[j];
if (p[i] == p[j + 1]) j ++ ;
next[i] = j;
}
for (int i = 1, j = 0; i <= n; i ++ ) {
while (j && s[i] != p[j + 1]) j = next[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m) return i - m;
}
return -1;
}
};
作者:yxc
链接:https://www.acwing.com/activity/content/code/content/347914/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
总结
- 今天两道简单的leetcode做完了,发现自己容易把问题想复杂,完全没有意义,简单题,怎么想怎么来。
- 然后算法题复习题,又被背包问题给难住了,实际上能够写出状态转移方程,但是觉得有点麻烦,那个完全背包问题就划水划过去了。明天重点看一下这道题,然后再随便找一道区间DP的新题。








![[数据概念]一分钟弄懂数据治理](https://img-blog.csdnimg.cn/img_convert/2ef2a15ebfc232c59f94db3a4df1e7c9.jpeg)