1 概要
1.EM算法是含有隐变量的概率模型极大似然估计或极大后验概率估计的迭代算法。含有隐变量的概率模型的数据表示为 P ( Y , Z ∣ θ ) P(Y,Z|\theta) P(Y,Z∣θ)。这里, Y Y Y是观测变量的数据, Z Z Z是隐变量的数据, θ \theta θ 是模型参数。EM算法通过迭代求解观测数据的对数似然函数 L ( θ ) = log P ( Y ∣ θ ) {L}(\theta)=\log {P}(\mathrm{Y} | \theta) L(θ)=logP(Y∣θ)的极大化,实现极大似然估计。每次迭代包括两步:
E E E步,求期望,即求 l o g P ( Y , Z ∣ Y , θ ) logP\left(Y,Z | Y, \theta\right) logP(Y,Z∣Y,θ) )关于 P ( Z ∣ Y , θ ( i ) ) P\left(Z | Y, \theta^{(i)}\right) P(Z∣Y,θ(i)))的期望:
Q
(
θ
,
θ
(
i
)
)
=
∑
Z
log
P
(
Y
,
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
Q\left(\theta, \theta^{(i)}\right)=\sum_{Z} \log P(Y, Z | \theta) P\left(Z | Y, \theta^{(i)}\right)
Q(θ,θ(i))=Z∑logP(Y,Z∣θ)P(Z∣Y,θ(i))
称为
Q
Q
Q函数,这里
θ
(
i
)
\theta^{(i)}
θ(i)是参数的现估计值;
M M M步,求极大,即极大化 Q Q Q函数得到参数的新估计值:
θ ( i + 1 ) = arg max θ Q ( θ , θ ( i ) ) \theta^{(i+1)}=\arg \max _{\theta} Q\left(\theta, \theta^{(i)}\right) θ(i+1)=argθmaxQ(θ,θ(i))
在构建具体的EM算法时,重要的是定义 Q Q Q函数。每次迭代中,EM算法通过极大化 Q Q Q函数来增大对数似然函数 L ( θ ) {L}(\theta) L(θ)。
2.EM算法在每次迭代后均提高观测数据的似然函数值,即
P ( Y ∣ θ ( i + 1 ) ) ⩾ P ( Y ∣ θ ( i ) ) P\left(Y | \theta^{(i+1)}\right) \geqslant P\left(Y | \theta^{(i)}\right) P(Y∣θ(i+1))⩾P(Y∣θ(i))
在一般条件下EM算法是收敛的,但不能保证收敛到全局最优。
3.EM算法应用极其广泛,主要应用于含有隐变量的概率模型的学习。高斯混合模型的参数估计是EM算法的一个重要应用,下一章将要介绍的隐马尔可夫模型的非监督学习也是EM算法的一个重要应用。
4.EM算法还可以解释为 F F F函数的极大-极大算法。EM算法有许多变形,如GEM算法。GEM算法的特点是每次迭代增加 F F F函数值(并不一定是极大化 F F F函数),从而增加似然函数值。
关于EM算法的数学推导可以见文章:EM算法数学推导
2 书中例题

观测数据的似然函数: P ( Y ∣ θ ) = ∏ j = 1 n [ π p y j ( 1 − p ) 1 − y j + ( 1 − π ) q y j ( 1 − q ) 1 − y j ] P(Y|\theta) = \prod_{j=1}^{n}[\pi p^{y_j}(1-p)^{1-y_j}+(1-\pi) q^{y_j}(1-q)^{1-y_j}] P(Y∣θ)=j=1∏n[πpyj(1−p)1−yj+(1−π)qyj(1−q)1−yj]
E step:计算在模型参数 π ( i ) , p ( i ) , q ( i ) \pi^{(i)},p^{(i)},q^{(i)} π(i),p(i),q(i)下观测数据 y j y_j yj来自掷硬币B的概率。
μ j ( i + 1 ) = π ( i ) ( p ( i ) ) y j ( 1 − ( p ( i ) ) 1 − y j π ( i ) ( p ( i ) ) y j ( 1 − ( p ( i ) ) 1 − y j + ( 1 − π ( i ) ) ( q ( i ) ) y j ( 1 − q ( i ) ) 1 − y j \mu^{(i+1)}_j=\frac{\pi^{(i)} (p^{(i)})^{y_j}(1-(p^{(i)})^{1-y_j}}{\pi^{(i)} (p^{(i)})^{y_j}(1-(p^{(i)})^{1-y_j}+(1-\pi^{(i)}) (q^{(i)})^{y_j}(1-q^{(i)})^{1-y_j}} μj(i+1)=π(i)(p(i))yj(1−(p(i))1−yj+(1−π(i))(q(i))yj(1−q(i))1−yjπ(i)(p(i))yj(1−(p(i))1−yj
M step:计算模型参数的新估计值。
π ( i + 1 ) = 1 n ∑ j = 1 n μ j ( i + 1 ) \pi^{(i+1)}=\frac{1}{n}\sum_{j=1}^n\mu^{(i+1)}_j π(i+1)=n1j=1∑nμj(i+1)
p ( i + 1 ) = ∑ j = 1 n μ j ( i + 1 ) y j ∑ j = 1 n μ j ( i + 1 ) p^{(i+1)}=\frac{\sum_{j=1}^n\mu^{(i+1)}_jy_j}{\sum_{j=1}^n\mu^{(i+1)}_j} p(i+1)=∑j=1nμj(i+1)∑j=1nμj(i+1)yj
q ( i + 1 ) = ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) y j ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) q^{(i+1)}=\frac{\sum_{j=1}^n(1-\mu^{(i+1)}_j)y_j}{\sum_{j=1}^n(1-\mu^{(i+1)}_j)} q(i+1)=∑j=1n(1−μj(i+1))∑j=1n(1−μj(i+1))yj
import math
class EM:
def __init__(self, prob):
self.pro_A, self.pro_B, self.pro_C = prob
# e_step
def pmf(self, i):
pro_1 = self.pro_A * math.pow(self.pro_B, data[i]) * math.pow(
(1 - self.pro_B), 1 - data[i])
pro_2 = (1 - self.pro_A) * math.pow(self.pro_C, data[i]) * math.pow(
(1 - self.pro_C), 1 - data[i])
return pro_1 / (pro_1 + pro_2)
# m_step
def fit(self, data):
count = len(data)
print('init prob:{}, {}, {}'.format(self.pro_A, self.pro_B,
self.pro_C))
for d in range(count):
_ = yield
_pmf = [self.pmf(k) for k in range(count)]
pro_A = 1 / count * sum(_pmf)
pro_B = sum([_pmf[k] * data[k] for k in range(count)]) / sum(
[_pmf[k] for k in range(count)])
pro_C = sum([(1 - _pmf[k]) * data[k]
for k in range(count)]) / sum([(1 - _pmf[k])
for k in range(count)])
print('{}/{} pro_a:{:.3f}, pro_b:{:.3f}, pro_c:{:.3f}'.format(
d + 1, count, pro_A, pro_B, pro_C))
self.pro_A = pro_A
self.pro_B = pro_B
self.pro_C = pro_C
data = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1]
em = EM(prob=[0.5, 0.5, 0.5]) # 初值都设置为0.5
f = em.fit(data)
next(f) # 开始生成器
init prob:0.5, 0.5, 0.5
# 第一次迭代
f.send(1)
1/10 pro_a:0.500, pro_b:0.600, pro_c:0.600
# 第二次
f.send(2)
2/10 pro_a:0.500, pro_b:0.600, pro_c:0.600
em = EM(prob=[0.4, 0.6, 0.7]) # 换另一些初值
f2 = em.fit(data)
next(f2)
init prob:0.4, 0.6, 0.7
f2.send(1)
1/10 pro_a:0.406, pro_b:0.537, pro_c:0.643
f2.send(2)
2/10 pro_a:0.406, pro_b:0.537, pro_c:0.643
3 高斯混合模型(GMM)
高斯混合模型是一种概率模型,用于表示具有多个高斯分布成分的数据集。假设有一个由 K K K 个高斯分布组成的混合模型,其概率密度函数可以表示为:
p ( x ) = ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) p(x) = \sum_{k=1}^K \pi_k \mathcal{N}(x \mid \mu_k, \Sigma_k) p(x)=k=1∑KπkN(x∣μk,Σk)
其中:
- π k \pi_k πk 是第 k k k 个高斯成分的权重,满足 ∑ k = 1 K π k = 1 \sum_{k=1}^K \pi_k = 1 ∑k=1Kπk=1 且 π k ≥ 0 \pi_k \geq 0 πk≥0。
- N ( x ∣ μ k , Σ k ) \mathcal{N}(x \mid \mu_k, \Sigma_k) N(x∣μk,Σk) 是均值为 μ k \mu_k μk、协方差为 Σ k \Sigma_k Σk 的高斯分布。
EM算法求解步骤
EM算法用于最大化具有隐变量模型的似然函数。对于GMM,隐变量是指每个数据点属于哪个高斯成分。EM算法的步骤包括E步和M步,具体如下:
初始化
- 初始化参数 { π k ( 0 ) , μ k ( 0 ) , Σ k ( 0 ) } \{\pi_k^{(0)}, \mu_k^{(0)}, \Sigma_k^{(0)}\} {πk(0),μk(0),Σk(0)}。
- 计算初始的对数似然函数值。
E步(Expectation Step)
计算第 i i i 个数据点属于第 k k k 个高斯成分的后验概率,即责任(又称响应度):
γ i k ( t ) = π k ( t ) N ( x i ∣ μ k ( t ) , Σ k ( t ) ) ∑ j = 1 K π j ( t ) N ( x i ∣ μ j ( t ) , Σ j ( t ) ) \gamma_{ik}^{(t)} = \frac{\pi_k^{(t)} \mathcal{N}(x_i \mid \mu_k^{(t)}, \Sigma_k^{(t)})}{\sum_{j=1}^K \pi_j^{(t)} \mathcal{N}(x_i \mid \mu_j^{(t)}, \Sigma_j^{(t)})} γik(t)=∑j=1Kπj(t)N(xi∣μj(t),Σj(t))πk(t)N(xi∣μk(t),Σk(t))
M步(Maximization Step)
更新参数:
- 更新混合系数:
π k ( t + 1 ) = 1 N ∑ i = 1 N γ i k ( t ) \pi_k^{(t+1)} = \frac{1}{N} \sum_{i=1}^N \gamma_{ik}^{(t)} πk(t+1)=N1i=1∑Nγik(t)
- 更新均值:
μ k ( t + 1 ) = ∑ i = 1 N γ i k ( t ) x i ∑ i = 1 N γ i k ( t ) \mu_k^{(t+1)} = \frac{\sum_{i=1}^N \gamma_{ik}^{(t)} x_i}{\sum_{i=1}^N \gamma_{ik}^{(t)}} μk(t+1)=∑i=1Nγik(t)∑i=1Nγik(t)xi
- 更新协方差矩阵:
Σ k ( t + 1 ) = ∑ i = 1 N γ i k ( t ) ( x i − μ k ( t + 1 ) ) ( x i − μ k ( t + 1 ) ) T ∑ i = 1 N γ i k ( t ) \Sigma_k^{(t+1)} = \frac{\sum_{i=1}^N \gamma_{ik}^{(t)} (x_i - \mu_k^{(t+1)})(x_i - \mu_k^{(t+1)})^T}{\sum_{i=1}^N \gamma_{ik}^{(t)}} Σk(t+1)=∑i=1Nγik(t)∑i=1Nγik(t)(xi−μk(t+1))(xi−μk(t+1))T
收敛判定
计算当前的对数似然函数值,如果其增量小于预设的阈值,则算法收敛;否则,返回E步继续迭代。
4 第9章习题
习题9.1
如例9.1的三硬币模型,假设观测数据不变,试选择不同的处置,例如, π ( 0 ) = 0.46 , p ( 0 ) = 0.55 , q ( 0 ) = 0.67 \pi^{(0)}=0.46,p^{(0)}=0.55,q^{(0)}=0.67 π(0)=0.46,p(0)=0.55,q(0)=0.67,求模型参数为 θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q)的极大似然估计。
解答:
import numpy as np
import math
class EM:
def __init__(self, prob):
self.pro_A, self.pro_B, self.pro_C = prob
def pmf(self, i):
pro_1 = self.pro_A * math.pow(self.pro_B, data[i]) * math.pow(
(1 - self.pro_B), 1 - data[i])
pro_2 = (1 - self.pro_A) * math.pow(self.pro_C, data[i]) * math.pow(
(1 - self.pro_C), 1 - data[i])
return pro_1 / (pro_1 + pro_2)
def fit(self, data):
print('init prob:{}, {}, {}'.format(self.pro_A, self.pro_B,
self.pro_C))
count = len(data)
theta = 1
d = 0
while (theta > 0.00001):
# 迭代阻塞
_pmf = [self.pmf(k) for k in range(count)]
pro_A = 1 / count * sum(_pmf)
pro_B = sum([_pmf[k] * data[k] for k in range(count)]) / sum(
[_pmf[k] for k in range(count)])
pro_C = sum([(1 - _pmf[k]) * data[k]
for k in range(count)]) / sum([(1 - _pmf[k])
for k in range(count)])
d += 1
print('{} pro_a:{:.4f}, pro_b:{:.4f}, pro_c:{:.4f}'.format(
d, pro_A, pro_B, pro_C))
theta = abs(self.pro_A - pro_A) + abs(self.pro_B -
pro_B) + abs(self.pro_C -
pro_C)
self.pro_A = pro_A
self.pro_B = pro_B
self.pro_C = pro_C
# 加载数据
data = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1]
em = EM(prob=[0.46, 0.55, 0.67])
f = em.fit(data)
init prob:0.46, 0.55, 0.67
1 pro_a:0.4619, pro_b:0.5346, pro_c:0.6561
2 pro_a:0.4619, pro_b:0.5346, pro_c:0.6561
习题9.2
过于简单,略。
习题9.3
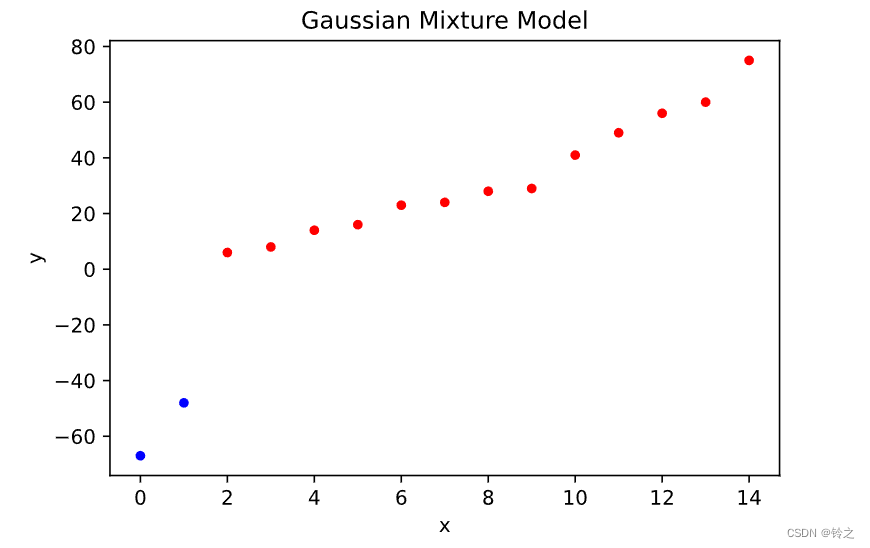
已知观测数据:-67,-48,6,8,14,16,23,24,28,29,41,49,56,60,75。试估计两个分量的高斯混合模型的5个参数。
解答:
from sklearn.mixture import GaussianMixture # 用于高斯混合模型的实现
import numpy as np
import matplotlib.pyplot as plt
# 初始化观测数据
data = np.array([-67, -48, 6, 8, 14, 16, 23, 24, 28, 29, 41, 49, 56, 60, 75]).reshape(-1, 1)
# 聚类。指定混合成分的数量为2(即模型中有两个高斯分布)
gmmModel = GaussianMixture(n_components=2)
gmmModel.fit(data)
labels = gmmModel.predict(data)
print("labels =", labels) # 输出每个数据点所属的高斯分布的标签
print("Means =", gmmModel.means_.reshape(1, -1))
print("Covariances =", gmmModel.covariances_.reshape(1, -1))
print("Mixing Weights = ", gmmModel.weights_.reshape(1, -1))
labels = [1 1 0 0 0 0 0 0 0 0 0 0 0 0 0]
Means = [[ 32.98489643 -57.51107027]]
Covariances = [[429.45764867 90.24987882]]
Mixing Weights = [[0.86682762 0.13317238]]
import matplotlib.pyplot as plt
from matplotlib_inline import backend_inline
backend_inline.set_matplotlib_formats('svg')
for i in range(0, len(labels)):
if labels[i] == 0:
plt.scatter(i, data.take(i), s=15, c='red')
elif labels[i] == 1:
plt.scatter(i, data.take(i), s=15, c='blue')
plt.title('Gaussian Mixture Model')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
习题9.4
EM算法可以用到朴素贝叶斯法的非监督学习,试写出其算法。
解答:
EM算法的一般化:
E步骤:
根据参数初始化或上一次迭代的模型参数来计算出隐变量的后验概率,其实就是隐变量的期望。作为隐变量的现估计值:
w
j
(
i
)
=
Q
i
(
z
(
i
)
=
j
)
:
=
p
(
z
(
i
)
=
j
∣
x
(
i
)
;
θ
)
w_j^{(i)}=Q_{i}(z^{(i)}=j) := p(z^{(i)}=j | x^{(i)} ; \theta)
wj(i)=Qi(z(i)=j):=p(z(i)=j∣x(i);θ)
M步骤:
将似然函数最大化以获得新的参数值:
θ
:
=
arg
max
θ
∑
i
∑
z
(
i
)
Q
i
(
z
(
i
)
)
log
p
(
x
(
i
)
,
z
(
i
)
;
θ
)
Q
i
(
z
(
i
)
)
\theta :=\arg \max_{\theta} \sum_i \sum_{z^{(i)}} Q_i (z^{(i)}) \log \frac{p(x^{(i)}, z^{(i)} ; \theta)}{Q_i (z^{(i)})}
θ:=argθmaxi∑z(i)∑Qi(z(i))logQi(z(i))p(x(i),z(i);θ)
使用NBMM(朴素贝叶斯的混合模型)中的 ϕ z , ϕ j ∣ z ( i ) = 1 , ϕ j ∣ z ( i ) = 0 \phi_z,\phi_{j|z^{(i)}=1},\phi_{j|z^{(i)}=0} ϕz,ϕj∣z(i)=1,ϕj∣z(i)=0参数替换一般化的EM算法中的 θ \theta θ参数,然后依次求解 w j ( i ) w_j^{(i)} wj(i)与 ϕ z , ϕ j ∣ z ( i ) = 1 , ϕ j ∣ z ( i ) = 0 \phi_z,\phi_{j|z^{(i)}=1},\phi_{j|z^{(i)}=0} ϕz,ϕj∣z(i)=1,ϕj∣z(i)=0参数的更新问题。
NBMM的EM算法:
E步骤:
w
j
(
i
)
:
=
P
(
z
(
i
)
=
1
∣
x
(
i
)
;
ϕ
z
,
ϕ
j
∣
z
(
i
)
=
1
,
ϕ
j
∣
z
(
i
)
=
0
)
w_j^{(i)}:=P\left(z^{(i)}=1 | x^{(i)} ; \phi_z, \phi_{j | z^{(i)}=1}, \phi_{j | z^{(i)}=0}\right)
wj(i):=P(z(i)=1∣x(i);ϕz,ϕj∣z(i)=1,ϕj∣z(i)=0)
M步骤:
ϕ
j
∣
z
(
i
)
=
1
:
=
∑
i
=
1
m
w
(
i
)
I
(
x
j
(
i
)
=
1
)
∑
i
=
1
m
w
(
i
)
ϕ
j
∣
z
(
i
)
=
0
:
=
∑
i
=
1
m
(
1
−
w
(
i
)
)
I
(
x
j
(
i
)
=
1
)
∑
i
=
1
m
(
1
−
w
(
i
)
)
ϕ
z
(
i
)
:
=
∑
i
=
1
m
w
(
i
)
m
\phi_{j | z^{(i)}=1} :=\frac{\displaystyle \sum_{i=1}^{m} w^{(i)} I(x_{j}^{(i)}=1)}{\displaystyle \sum_{i=1}^{m} w^{(i)}} \\ \phi_{j | z^{(i)}=0}:= \frac{\displaystyle \sum_{i=1}^{m}\left(1-w^{(i)}\right) I(x_{j}^{(i)}=1)}{ \displaystyle \sum_{i=1}^{m}\left(1-w^{(i)}\right)} \\ \phi_{z^{(i)}} :=\frac{\displaystyle \sum_{i=1}^{m} w^{(i)}}{m}
ϕj∣z(i)=1:=i=1∑mw(i)i=1∑mw(i)I(xj(i)=1)ϕj∣z(i)=0:=i=1∑m(1−w(i))i=1∑m(1−w(i))I(xj(i)=1)ϕz(i):=mi=1∑mw(i)
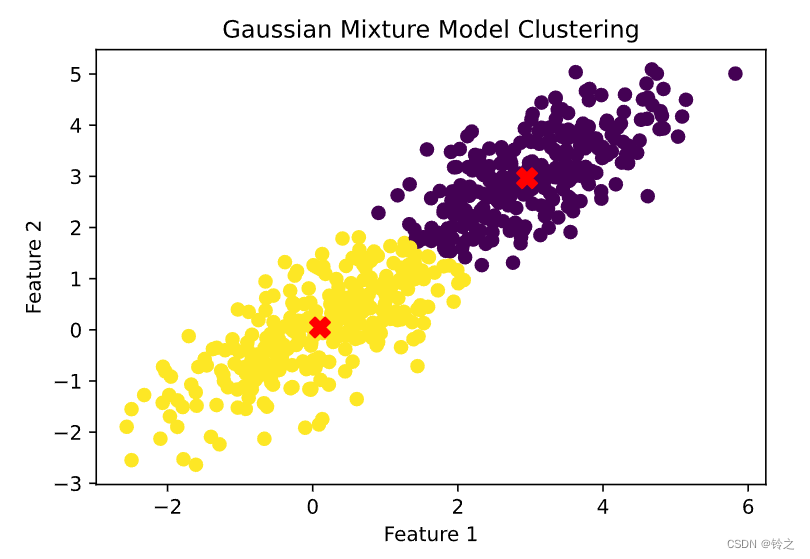
5 一个例子
使用Python和scikit-learn库来实现高斯混合模型,并应用EM算法进行参数估计。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
# 生成数据
np.random.seed(0)
n_samples = 300
# 生成第一个高斯分布的数据
mean1 = [0, 0]
cov1 = [[1, 0.75], [0.75, 1]]
data1 = np.random.multivariate_normal(mean1, cov1, n_samples)
# 生成第二个高斯分布的数据
mean2 = [3, 3]
cov2 = [[1, 0.75], [0.75, 1]]
data2 = np.random.multivariate_normal(mean2, cov2, n_samples)
# 合并数据
data = np.vstack((data1, data2))
# 创建并拟合高斯混合模型
gmm = GaussianMixture(n_components=2, covariance_type='full', random_state=0)
gmm.fit(data)
# 预测每个数据点的类别标签
labels = gmm.predict(data)
# 获取模型参数
weights = gmm.weights_
means = gmm.means_
covariances = gmm.covariances_
print("Mixing Weights (混合系数):", weights)
print("Means (均值):", means)
print("Covariances (协方差矩阵):", covariances)
# 可视化结果
plt.scatter(data[:, 0], data[:, 1], c=labels, s=40, cmap='viridis', zorder=2)
plt.scatter(means[:, 0], means[:, 1], c='red', s=100, marker='X', zorder=3)
plt.title("Gaussian Mixture Model Clustering")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()
Mixing Weights (混合系数): [0.49842773 0.50157227]
Means (均值): [[2.95306327 2.96316145]
[0.10026529 0.04560121]]
Covariances (协方差矩阵): [[[0.89428558 0.60641642]
[0.60641642 0.77687958]]
[[1.05451964 0.7500382 ]
[0.7500382 0.94281161]]]
代码来自:https://github.com/fengdu78/lihang-code
参考书籍:李航《机器学习方法》