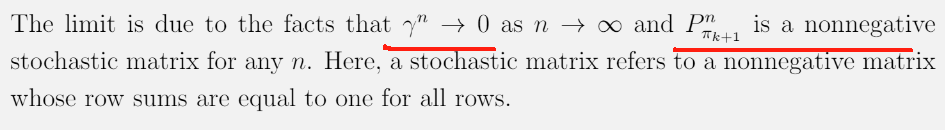PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍
- 1、视频 + 学堂在线 习题
- 2、过 电子书 补充 【下载: 本章 PDF 电子书 GitHub】 [又看了一遍视频。原来第一次跳过了好多内容。。。]
- 3、总体 MOOC 过一遍 习题
学堂在线 课程页面链接
中国大学MOOC 课程页面链接
B 站 视频链接
PPT和书籍下载网址: 【GitHub 链接】

总述:
开始介绍第一个可以找到最优策略的算法。 ——> 动态规划算法
介绍 3 种 迭代算法:
1、值迭代算法: 上一章讨论的求解 Bellman 最优方程的压缩映射定理 所提出的算法。
2、策略迭代算法
3、截断策略迭代算法: 值迭代 和 策略迭代 算法是该算法的极端情况。
动态规划 算法,需要系统模型。
本章介绍的策略迭代算法 扩展得到 第 5 章介绍的蒙特卡洛算法。
——————————————
model-based 算法
值迭代 上一章 的延伸
策略迭代 下一章 蒙特卡洛学习的基础

值迭代 和 策略迭代 是 截断策略迭代 的两个极端情况
4.1 值迭代
贝尔曼最优公式 的 矩阵向量形式:
v = f ( v ) = max π ( r π + γ P π v ) \bm v=f(\bm v) =\max\limits_\pi({\bm r}_\pi+\gamma {\bm P}_\pi {\bm v}) v=f(v)=πmax(rπ+γPπv)
求解方法: 上一章 的 压缩映射定理 建议的迭代算法 【值迭代】
v k + 1 = f ( v k ) = max π ( r π + γ P π v k ) , k = 1 , 2 , 3... {\bm v}_{k+1} = f({\bm v}_k)=\max\limits_\pi({\bm r}_\pi+\gamma {\bm P}_\pi {\bm v}_k), ~~~k=1, 2, 3... vk+1=f(vk)=πmax(rπ+γPπvk), k=1,2,3...
其中 v 0 {\bm v}_0 v0 可为任意值。
两步:
1、策略 更新 (policy update)
- v k {\bm v}_k vk 给定, 求解 π k + 1 = arg max π ( r π + γ P π v k ) \pi_{k+1} = \arg \max\limits_{\pi}({\bm r}_\pi+\gamma {\bm P}_\pi {\bm v}_k) πk+1=argπmax(rπ+γPπvk)
2、值 更新 (value update)
- 上一步得到的策略 π k + 1 \pi_{k+1} πk+1, 更新 v k + 1 = r π k + 1 + γ P π k + 1 v k {\bm v}_{k +1}={\bm r}_{\pi_{k+1}}+\gamma {\bm P}_{\pi_{k+1}}{\bm v}_k vk+1=rπk+1+γPπk+1vk

v
k
v_k
vk 是否是一个状态值?
答案是否定的。虽然
v
k
v_k
vk 最终收敛于最优状态值,但不能保证满足任何策略的 Bellman方程。例如,它一般不满足
v
k
=
r
π
k
+
γ
P
π
k
v
k
v_k=r_{\pi_k}+\gamma P_{\pi_k}v_k
vk=rπk+γPπkvk 或
v
k
=
r
π
k
+
1
+
γ
P
π
k
+
1
v
k
v_k=r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_k
vk=rπk+1+γPπk+1vk。它只是算法生成的一个中间值。另外,由于
v
k
v_k
vk 不是状态值,所以
q
k
q_k
qk 不是动作值。
编程实现 需要知道 更具体的形式 elementwise form
更新策略 更具体的形式为:
π k + 1 ( s ) = arg max π ∑ a π ( a ∣ s ) ( ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v k ( s ′ ) ) ⏟ q k ( s , a ) , s ∈ S \pi_{k+1}(s) = \arg \max\limits_{\pi}\sum_a\pi(a|s)\underbrace{\Big(\sum_rp(r|s, a)r+\gamma \sum_{s^{\prime}}p(s^{\prime}|s, a)v_k(s^{\prime})\Big)}_{q_k(s, a)},s \in S πk+1(s)=argπmaxa∑π(a∣s)qk(s,a) (r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vk(s′)),s∈S根据上一章的分析,上述优化问题的最优策略解为:
π k + 1 ( a ∣ s ) = { 1 a = a k ∗ ( s ) 0 a ≠ a k ∗ ( s ) \pi_{k+1}(a|s)=\begin{cases}1\quad a=a_k^*(s) \\ 0\quad a\neq a_k^*(s) \end{cases} πk+1(a∣s)={1a=ak∗(s)0a=ak∗(s)
其中 a k ∗ ( s ) = arg max a q k ( a , s ) a_k^*(s)=\arg\max\limits_aq_k(a, s) ak∗(s)=argamaxqk(a,s)
- 如果 a k ∗ ( s ) = arg max a q k ( a , s ) a_k^*(s)=\arg\max\limits_aq_k(a, s) ak∗(s)=argamaxqk(a,s) 有多个解,我们可以选择任意一个解而不影响算法的收敛性。 只是若是没选中最优策略该选的动作,需要多迭代几次后才能获得最终的最优策略
贪心策略 π k + 1 \pi_{k+1} πk+1:贪心地选择 q k ( a , s ) q_k(a, s) qk(a,s) 最大的 action ~~~ 确定的策略
————————————
更新值 更具体的形式为:
v k + 1 ( s ) = ∑ a π k + 1 ( a ∣ s ) ( ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v k ( s ′ ) ) ⏟ q k ( s , a ) , s ∈ S = max a q k ( a , s ) \begin{align*}v_{k +1}(s)&=\sum_a\pi_{k+1}(a|s)\underbrace{\Big(\sum_rp(r|s, a)r+\gamma \sum_{s^{\prime}}p(s^{\prime}|s, a)v_k(s^{\prime})\Big)}_{q_k(s, a)},s \in S\\ &=\max_aq_k(a, s)\end{align*} vk+1(s)=a∑πk+1(a∣s)qk(s,a) (r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vk(s′)),s∈S=amaxqk(a,s)
迭代流程
v k ( s ) → q k ( s , a ) → v_k(s)\to q_k(s, a)\to vk(s)→qk(s,a)→ 贪心策略 π k + 1 ( a ∣ s ) → ~\pi_{k+1}(a|s)\to πk+1(a∣s)→ 新的值 v k + 1 = max a q k ( s , a ) ~v_{k+1}=\max\limits_{a}q_k(s, a) vk+1=amaxqk(s,a)
伪代码: 值迭代算法
目标: 搜索 求解 贝尔曼最优公式的 最优状态值 和 最优策略。

遍历 每个状态 中的 每个动作, 计算 q k q_k qk
- 策略 更新: 选择 q k q_k qk 最大的 action
- 值 更新: 将 v k + 1 ( s ) v_{k+1}(s) vk+1(s) 更新为 计算得到的最大 q k q_k qk
4.1.2 例子
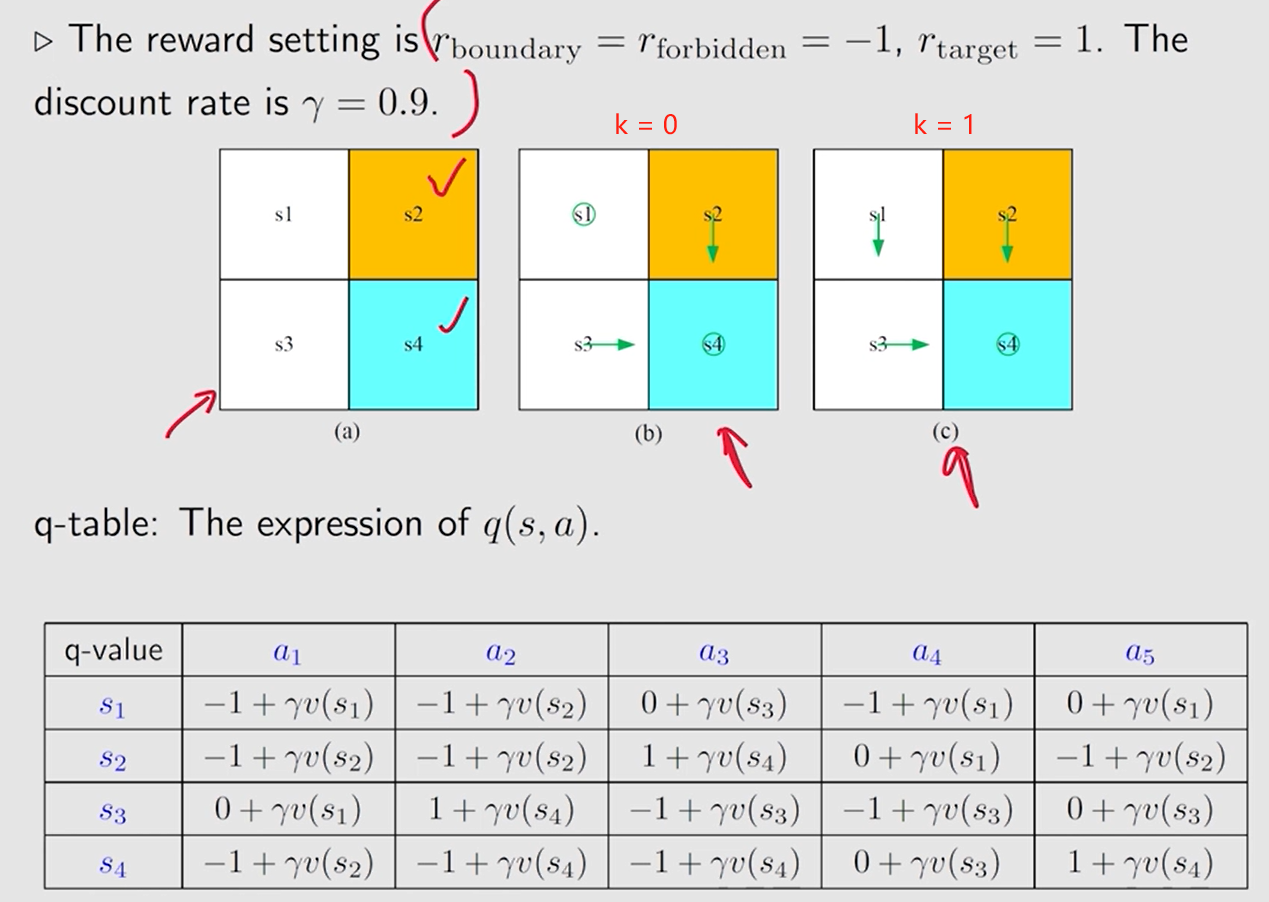
对 每个状态 的 每个动作 ,初始化 q q q 值表
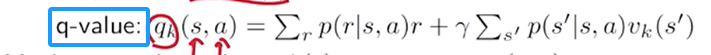

按照这里
策略更新 是将 每个状态 的
q
q
q 值最大的动作 的选取概率
π
(
a
∣
s
)
\pi(a|s)
π(a∣s) 置为 1。
~~~
等效于 让策略在这一步 做这个
q
q
q 值最大的动作
值更新 是将 每个状态 的 值更新为 相应状态的最大
q
q
q 值。
v
0
v_0
v0 可以任意选取,这里选择为 0。 不同的初值选取对迭代过程影响多大?如何根据具体情况选取合适的初值?
——> 比较直觉的是若是初始值选得离最优状态值较远, 需要的迭代次数会多些。
对于 状态
s
1
s_1
s1,动作
a
3
a_3
a3 和
a
5
a_5
a5 对应的
q
q
q 都是最大的, 这里直接选了
a
5
a_5
a5, 有没有可能在这里选
a
3
a_3
a3 得到的才是最优策略呢?
——> 确实有可能, 所以要多次迭代,收敛后迭代结束获得的就是 最优策略。
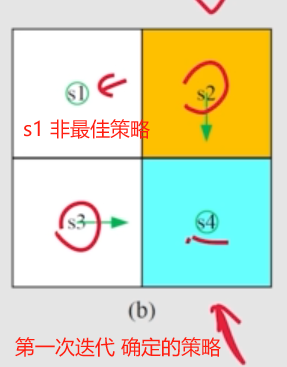
第一次 迭代, s1 没有达到 最优。

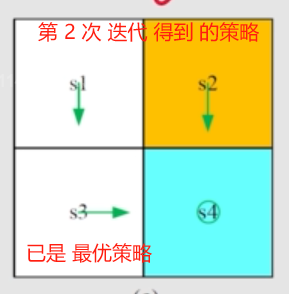
这里 迭代两次 就获得了 最优策略。
其它 更复杂情况 的迭代停止条件为:

迭代停止 则认为 获得了 最优策略。
4.2 策略迭代
主要内容: 是什么?——> 性质 ——> 如何 编程实现
任意给定的初始策略 π 0 \pi_0 π0
两步:
1、策略 评估 (policy evaluation, PE)
- 计算 π k \pi_k πk 的状态值: v π k = r π k + γ P π k v π k {\bm v}_{\pi_k}={\bm r}_{\pi_k}+\gamma {\bm P}_{\pi_k}{\bm v}_{\pi_k}~~~~~~~ vπk=rπk+γPπkvπk 求解 贝尔曼方程
策略评估做的事:通过计算相应的 状态值 来评估给定策略。
2、策略 优化 (policy improvement,PI)
- π k + 1 = arg max π ( r π + γ P π v π k ) \pi_{k+1}=\arg\max\limits_\pi({\bm r}_\pi+\gamma {\bm P}_\pi {\bm v}_{\pi_k}) πk+1=argπmax(rπ+γPπvπk)
迭代流程
π 0 → P E v π 0 → P I π 1 → P E v π 1 → P I π 2 → P E v π 2 → P I . . . \pi_0\xrightarrow{PE}v_{\pi_0}\xrightarrow{PI}\pi_1\xrightarrow{PE}v_{\pi_1}\xrightarrow{PI}\pi_2\xrightarrow{PE}v_{\pi_2}\xrightarrow{PI}... π0PEvπ0PIπ1PEvπ1PIπ2PEvπ2PI...
PE: 策略 评估
PI:策略 优化
现在处理以下几个问题:
Q1:在策略评估步骤中,如何通过求解 Bellman 方程得到状态值?
Q2:在策略优化步骤中,为什么新策略
π
k
+
1
\pi_{k+1}
πk+1 优于
π
k
π_k
πk?
Q3:为什么这样的迭代算法最终可以达到最优策略?
Q4:这个策略迭代算法和之前的值迭代算法是什么关系?
Q1:在策略评估步骤中,如何通过求解 Bellman 方程得到状态值?
如何 获取 v π k v_{\pi_k} vπk
已知: v π k = r π k + γ P π k v π k {\bm v}_{\pi_k}={\bm r}_{\pi_k}+\gamma {\bm P}_{\pi_k}{\bm v}_{\pi_k} vπk=rπk+γPπkvπk
方法一: 矩阵求逆
v π k = ( I − γ P π k ) − 1 r π k {\bm v}_{\pi_k}=({\bm I}-\gamma {\bm P}_{\pi_k})^{-1}{\bm r}_{\pi_k} vπk=(I−γPπk)−1rπk
方法二: 迭代 ✔
v π k ( j + 1 ) = r π k + γ P π k v π k ( j ) , j = 0 , 1 , 2 , . . . {\bm v}_{\pi_k}^{(j+1)}={\bm r}_{\pi_k}+\gamma {\bm P}_{\pi_k}{\bm v}_{\pi_k}^{(j)}, ~~~j=0,1,2,... vπk(j+1)=rπk+γPπkvπk(j), j=0,1,2,...
策略迭代 是在策略评估步骤中嵌入另一个迭代算法的迭代算法!
Q2:在策略优化步骤中,为什么新策略 π k + 1 \pi_{k+1} πk+1 优于 π k π_k πk?

- 证明 1: 在策略优化步骤中,为什么新策略 π k + 1 \pi_{k+1} πk+1 优于 π k π_k πk? ~~ P73-
Q3:为什么策略迭代算法最终可以找到最优策略?
由于每次迭代都会改进策略, 即
v π 0 ≤ v π 1 ≤ v π 2 ≤ ⋯ ≤ v π k ≤ ⋯ ≤ v ∗ \bm v_{\pi_0}\leq\bm v_{\pi_1}\leq\bm v_{\pi_2}\leq\cdots\leq\bm v_{\pi_k}\leq\cdots\leq\bm v^* vπ0≤vπ1≤vπ2≤⋯≤vπk≤⋯≤v∗
v π k \bm v_{\pi_k} vπk 不断减小并最终收敛。仍需证明 将收敛到 v ∗ \bm v^* v∗。

定理 4.1 (策略迭代的收敛性)。策略迭代算法生成的状态值序列 { v π k } k = 0 ∞ \{v_{\pi_k}\}_{k=0}^\infty {vπk}k=0∞ 收敛到最优状态值 v ∗ v^* v∗。因此,策略序列 { π k } k = 0 ∞ \{\pi_k\}_{k=0}^\infty {πk}k=0∞ 收敛到最优策略。
- 证明 2: 证明策略迭代会收敛到 最优策略 P75
证明的思路是证明 策略迭代算法 比 值迭代算法 收敛得更快。
如果 策略迭代 和 值迭代 从相同的初始猜测开始,由于 策略迭代 算法的收敛性,策略迭代 将比 值迭代 收敛得更快。
Q4:这个策略迭代算法和之前的值迭代算法是什么关系?
值迭代 和 策略迭代 是 截断策略迭代 的两个极端, 后续将进一步说明。
——————————————————
如何 实现 策略迭代算法?


策略迭代 算法:
目标: 搜索 最优状态值 和 最优策略

策略迭代算法 生成的中间值是是 状态值。 因为这些值是当前策略的 Bellman 方程的解。
4.2.3 例子
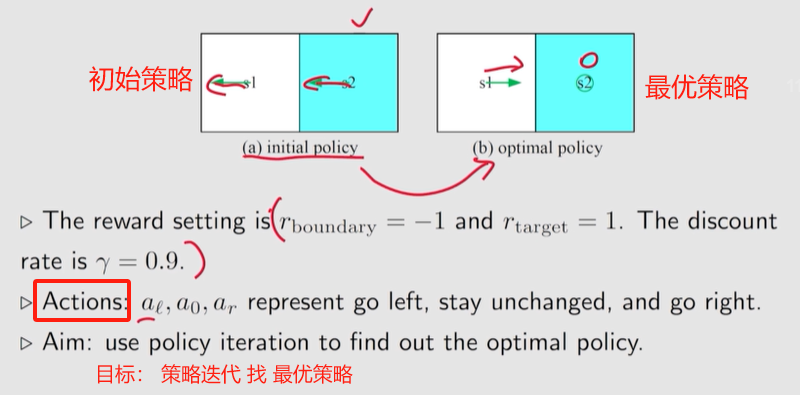


一个 示例 P79
发现一个有趣的现象:接近目标的状态 的策略 先变好, 远离目标的状态的策略会后变好。
在某一个状态, 选择 greedy action 时, 严重依赖于 其它状态的策略。
若其它状态的策略是不好的, 此时虽然选一个 动作值 (
q
q
q) 最大的 动作, 可能意义不大;
如果 其它状态 有能够到达目标区域 的策略, 选择变到那个状态,也能到达目标区域, 得到正的 reward。
当某个状态周围 没有状态 能够到达 目标区域 的时候, 这个状态无法到达目标区域。
当周围有状态能够到达目标区域的策略时, 新的策略也能到达目标区域。
1、观察策略是如何演变的,一个有趣的模式是靠近目标区域的状态比远离目标区域的状态更早找到最优策略。只有较近的状态能先找到到达目标的轨迹,较远的状态才能找到经过较近状态到达目标的轨迹。
2、状态值的空间分布呈现出一种有趣的模式:靠近目标的状态具有更大的状态值。这种模式的原因是,一个 agent 从更远的状态出发,必须走很多步才能获得正的奖励。这样的奖励将严重打折扣,因此相对较小。
4.3 截断策略迭代
值迭代 算法和 策略迭代 算法是截断策略迭代算法的两种特殊情况。
策略迭代:初始策略 为 π 0 \pi_0~~ π0 【任意猜测的】
- 策略评估 (PE): v π k = r π k + γ P π k v π k {\bm v}_{\pi_k}={\bm r}_{\pi_k}+\gamma {\bm P}_{\pi_k}{\bm v}_{\pi_k} vπk=rπk+γPπkvπk
- 策略优化 (PI): π k + 1 = arg max π ( r π + γ P π v π k ) \pi_{k+1}=\arg\max\limits_\pi({\bm r}_\pi+\gamma {\bm P}_\pi {\bm v}_{\pi_k}) πk+1=argπmax(rπ+γPπvπk)
值迭代:初始值 为 v 0 {\bm v}_0 v0
- 策略更新 (PU): π k + 1 = arg max π ( r π + γ P π v k ) \pi_{k+1}=\arg\max\limits_\pi({\bm r}_\pi+\gamma {\bm P}_\pi {\bm v}_k) πk+1=argπmax(rπ+γPπvk)
- 值更新 (VU): v k + 1 = r π k + 1 + γ P π k + 1 v k {\bm v}_{k+1}={\bm r}_{\pi_{k+1}}+\gamma {\bm P}_{\pi_{k+1}}{\bm v}_k vk+1=rπk+1+γPπk+1vk
!!每一步的等号右侧 都有的: r + γ P v {\bm r} +\gamma {\bm P} {\bm v} r+γPv


从相同的初始条件开始。
前三个步骤是相同的。
第四步就不一样了:
- 策略迭代,求解 v π 1 = r π 1 + γ P π 1 v π 1 v_{π_1} = r_{π_1} + γP_{\pi_1}v_{\pi_1} vπ1=rπ1+γPπ1vπ1 需要一个迭代算法 ( 迭代无数次 )
- 值迭代, v 1 = r π 1 + γ P π 1 v 0 v_1 = r_{π_1} + \gamma P_{π_1}v_0 v1=rπ1+γPπ1v0 是一步迭代。

每步求解 v \bm v v 值时, 值迭代 需要一步, 策略迭代需要无穷步,迭代次数取中间值如何呢?
值迭代算法:计算一次。
策略迭代算法:计算无限次迭代。
截断策略迭代算法:计算一个有限次迭代(例如
j
j
j )。从
j
j
j 到
∞
\infty
∞ 的其余迭代被截断。

算法中的 v k v_k vk 和 v k ( j ) v_k^{(j)} vk(j) 不是状态值,是真实状态值的近似值,因为在策略评估步骤中只执行有限次迭代。
只有当我们在 策略评估 步骤中运行无限次迭代时,才能获得真实的状态值。
截断策略迭代 会不会 结束迭代时是一个 发散的结果?

- 证明。参考 电子书 PDF P83
——————————————
证明: 截断策略迭代算法 的收敛性。
因为
v π k ( j ) = r π k + γ P π k v π k ( j − 1 ) v_{\pi_k}^{(j)}=r_{\pi_k}+\gamma P_{\pi_k}v_{\pi_k}^{(j-1)} vπk(j)=rπk+γPπkvπk(j−1)
v π k ( j + 1 ) = r π k + γ P π k v π k ( j ) v_{\pi_k}^{(j+1)}=r_{\pi_k}+\gamma P_{\pi_k}v_{\pi_k}^{(j)} vπk(j+1)=rπk+γPπkvπk(j)
则
v π k ( j + 1 ) − v π k ( j ) = γ P π k ( v π k ( j ) − v π k ( j − 1 ) ) = ⋯ = γ j P π k j ( v π k ( 1 ) − v π k ( 0 ) ) v_{\pi_k}^{(j+1)}-v_{\pi_k}^{(j)}=\gamma P_{\pi_k}(v_{\pi_k}^{(j)}-v_{\pi_k}^{(j-1)})=\cdots=\gamma^j P^j_{\pi_k}(v_{\pi_k}^{(1)}-v_{\pi_k}^{(0)}) vπk(j+1)−vπk(j)=γPπk(vπk(j)−vπk(j−1))=⋯=γjPπkj(vπk(1)−vπk(0))
v π k ( 0 ) = v π k − 1 v_{\pi_k}^{(0)}=v_{\pi_{k-1}}~~~~ vπk(0)=vπk−1 上一轮迭代的结果
v π k ( 1 ) = r π k + γ P π k v π k ( 0 ) = r π k + γ P π k v π k − 1 ≥ r π k − 1 + γ P π k − 1 v π k − 1 ① = v π k − 1 = v π k ( 0 ) \begin{aligned}v_{\pi_k}^{(1)}&=r_{\pi_k}+\gamma P_{\pi_k}v_{\pi_k}^{(0)}\\ &=r_{\pi_k}+\gamma P_{\pi_k}\textcolor{blue}{v_{\pi_{k-1}}}\\ &\geq r_{\pi_{\textcolor{blue}{{k-1}}}}+\gamma P_{\pi_{\textcolor{blue}{{k-1}}}}\textcolor{blue}{v_{\pi_{k-1}}}~~~~~~~~\textcolor{blue}{①}\\ &=v_{\pi_{k-1}}\\ &=v_{\pi_k}^{(0)}\end{aligned} vπk(1)=rπk+γPπkvπk(0)=rπk+γPπkvπk−1≥rπk−1+γPπk−1vπk−1 ①=vπk−1=vπk(0)
则 v π k ( j + 1 ) ≥ v π k ( j ) v_{\pi_k}^{(j+1)}\geq v_{\pi_k}^{(j)} vπk(j+1)≥vπk(j)。
① π k = arg max π ( r π + γ P π v π k − 1 ) \pi_k=\arg\max\limits_\pi(r_\pi+\gamma P_\pi v_{\pi_{k-1}}) πk=argπmax(rπ+γPπvπk−1)
——————————————
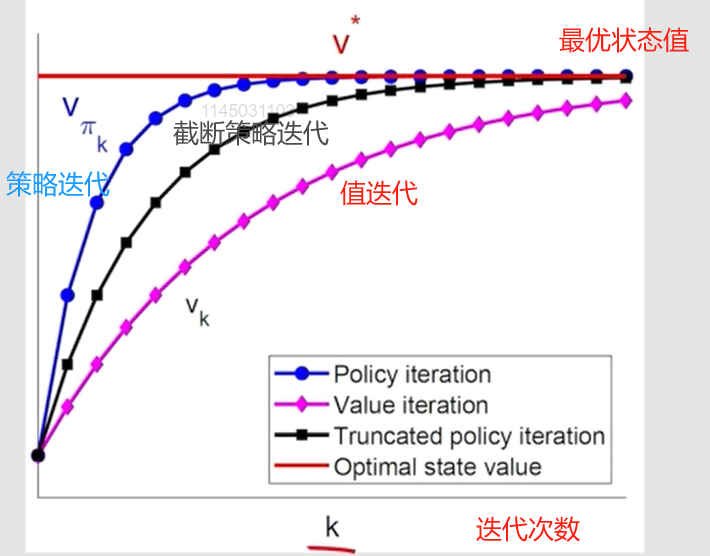
相比于策略迭代算法,截断的策略迭代算法在策略评估步骤中只需要有限次数的迭代,因此计算效率更高。与值迭代相比,截断策略迭代算法可以在策略评估步骤中多运行几次迭代,从而加快收敛速度。
Pl 【策略迭代】 的收敛性证明是基于 VI 【值迭代】 的收敛性证明。由于 VI 收敛,得到 PI 收敛。
小结:

4.5
Q:值迭代算法一定能找到最优策略吗?
是的。值迭代正是上一章求解 Bellman 最优性方程的 压缩映射定理 所提出的算法。利用 压缩映射定理 保证了算法的收敛性。
model-based VS model-free
虽然本章介绍的算法可以找到最优策略,但由于它们需要系统模型,通常被称为动态规划算法而不是强化学习算法。
强化学习算法可以分为两类:基于模型的和免模型的。
这里,“基于模型的”并不是指系统模型的需求。相反,基于模型的强化学习使用数据来估计系统模型,并在学习过程中使用该模型。相比之下,免模型强化学习在学习过程中不涉及模型估计。
——————
习题
值迭代、策略迭代、截断策略迭代
值迭代算法中间产生的值不一定对应某些策略的状态值,这些只是产生的一些中间过程的数值,没有特别的含义。
压缩映射定理给出的算法 实际是 值迭代算法。
策略迭代算法 同时获得 最优状态值 和 最优策略。 【策略评估 需要计算状态值】
补充
证明 1: 在策略优化步骤中,为什么新策略 π k + 1 \pi_{k+1} πk+1 优于 π k π_k πk? ~~ P73-
证明:
状态值 v π k + 1 v_{\pi_{k+1}} vπk+1 和 v π k v_{\pi_k} vπk 满足贝尔曼公式:
v π k + 1 = r π k + 1 + γ P π k + 1 v π k + 1 v_{\pi_{k+1}}=r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_{\pi_{k+1}} vπk+1=rπk+1+γPπk+1vπk+1
v π k = r π k + γ P π k v π k v_{\pi_k}=r_{\pi_k}+\gamma P_{\pi_k}v_{\pi_k} vπk=rπk+γPπkvπk
由于 π k + 1 = arg max π ( r π + γ P π v π k ) \pi_{k+1} = \arg\max\limits_\pi(r_\pi+\gamma P_\pi v_{\pi_k}) πk+1=argπmax(rπ+γPπvπk)
则 r π k + 1 + γ P π k + 1 v π k + 1 ≥ r π k + γ P π k v π k r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_{\pi_{k+1}}\geq r_{\pi_k}+\gamma P_{\pi_k}v_{\pi_k} rπk+1+γPπk+1vπk+1≥rπk+γPπkvπk
v π k − v π k + 1 = ( r π k + γ P π k v π k ) − ( r π k + 1 + γ P π k + 1 v π k + 1 ) ≤ ( r π k + 1 + γ P π k + 1 v π k ) − ( r π k + 1 + γ P π k + 1 v π k + 1 ) ≤ γ P π k + 1 ( v π k − v π k + 1 ) ≤ γ 2 P π k + 1 2 ( v π k − v π k + 1 ) ≤ . . . ≤ γ n P π k + 1 n ( v π k − v π k + 1 ) ≤ lim n → ∞ γ n P π k + 1 n ( v π k − v π k + 1 ) = 0 \begin{align*}v_{\pi_k}-v_{\pi_{k+1}}&= (r_{\pi_k}+\gamma P_{\pi_k}v_{\pi_k}) - (r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_{\pi_{k+1}})\\ &\leq(r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_{\pi_k}) - (r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_{\pi_{k+1}})\\ &\leq \gamma P_{\pi_{k+1}}(v_{\pi_k} -v_{\pi_{k+1}})\\ &\leq \gamma^2 P_{\pi_{k+1}}^2(v_{\pi_k} -v_{\pi_{k+1}})\\ &\leq ...\\ &\leq \gamma^n P_{\pi_{k+1}}^n(v_{\pi_k} -v_{\pi_{k+1}})\\ &\leq \lim\limits_{n\to\infty}\gamma^n P_{\pi_{k+1}}^n(v_{\pi_k} -v_{\pi_{k+1}})\\ &=0\end{align*} vπk−vπk+1=(rπk+γPπkvπk)−(rπk+1+γPπk+1vπk+1)≤(rπk+1+γPπk+1vπk)−(rπk+1+γPπk+1vπk+1)≤γPπk+1(vπk−vπk+1)≤γ2Pπk+12(vπk−vπk+1)≤...≤γnPπk+1n(vπk−vπk+1)≤n→∞limγnPπk+1n(vπk−vπk+1)=0
证明 2: 证明策略迭代会收敛到 最优策略 P75

定理 4.1 (策略迭代的收敛性)。策略迭代算法生成的状态值序列 { v π k } k = 0 ∞ \{v_{\pi_k}\}_{k=0}^\infty {vπk}k=0∞ 收敛到最优状态值 v ∗ v^* v∗。因此,策略序列 { π k } k = 0 ∞ \{\pi_k\}_{k=0}^\infty {πk}k=0∞ 收敛到最优策略。
证明的思路是证明 策略迭代算法 比 值迭代算法 收敛得更快。
——————————
证明:
为了 证明
{
v
π
k
}
k
=
0
∞
\{v_{\pi_k}\}_{k=0}^\infty
{vπk}k=0∞ 的收敛性, 引入由以下式子生成的 另一个序列
{
v
k
}
k
=
0
∞
\{v_k\}_{k=0}^\infty
{vk}k=0∞ 。
v k + 1 = f ( v k ) = max π ( r π + γ P π v k ) v_{k+1}=f(v_k)=\max\limits_\pi(r_\pi+\gamma P_\pi v_k) vk+1=f(vk)=πmax(rπ+γPπvk)
这个迭代算法 正是 值迭代算法,则给定任意初始值 v 0 v_0 v0, v k v_k vk 收敛到 v ∗ v^* v∗。
k = 1 k=1 k=1, 对任意 π 0 \pi_0 π0, 有 v π 0 ≥ v 0 v_{\pi_0}\geq v_0 vπ0≥v0。
通过 归纳法 证明 对任意 k k k, 有 v k ≤ v π k ≤ v ∗ v_k\leq v_{\pi_k}\leq v^* vk≤vπk≤v∗。
对 k ≥ 0 k\geq0 k≥0, 假设 v π k ≥ v k v_{\pi_k}\geq v_k vπk≥vk。
用到的一些中间式:

①
v
π
k
+
1
≥
v
π
k
v_{\pi_{k+1}}\geq v_{\pi_k}~~
vπk+1≥vπk 【上面的 证明 1 已证。即 策略优化后的策略的状态值 比之前的大】 ,
P
π
k
+
1
≥
0
P_{\pi_{k+1}}\geq0
Pπk+1≥0
② 令
π
k
′
=
arg
max
π
(
r
π
+
γ
P
π
v
k
)
{\textcolor{blue}{{\pi_k^\prime}}}=\arg \max\limits_\pi(r_\pi+\gamma P_\pi v_k)
πk′=argπmax(rπ+γPπvk)
③
π
k
+
1
=
arg
max
π
(
r
π
+
γ
P
π
v
π
k
)
\pi_{k+1}=\arg \max\limits_\pi(r_\pi+\gamma P_\pi v_{\pi_k})
πk+1=argπmax(rπ+γPπvπk)
对于 k + 1 k + 1 k+1 有:
v π k + 1 − v k + 1 = ( r π k + 1 + γ P π k + 1 v π k + 1 ) − max π ( r π + γ P π v k ) ≥ ( r π k + 1 + γ P π k + 1 v π k ) − max π ( r π + γ P π v k ) ① = ( r π k + 1 + γ P π k + 1 v π k ) − ( r π k ′ + γ P π k ′ v k ) ② ≥ ( r π k ′ + γ P π k ′ v π k ) − ( r π k ′ + γ P π k ′ v k ) ③ = γ P π k ′ ( v π k − v k ) \begin{aligned}v_{\pi_{k+1}}-v_{k+1}&=(r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_{\pi_{k+1}})-\max\limits_\pi(r_\pi+\gamma P_\pi v_k)\\ &\geq(r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_{\pi_{\textcolor{blue}{k}} })-\max\limits_\pi(r_\pi+\gamma P_\pi v_k)~~~~~~~~~~\textcolor{blue}{①}\\ &=(r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_{\pi_k })-(r_{\textcolor{blue}{{\pi_k^\prime}}}+\gamma P_{\textcolor{blue}{{\pi_k^\prime}}}v_k)~~~~~~~~~~\textcolor{blue}{②}\\ &\geq(r_{\textcolor{blue}{{\pi_k^\prime}}}+\gamma P_{\textcolor{blue}{{\pi_k^\prime}}}v_{\pi_k })-(r_{\textcolor{blue}{{\pi_k^\prime}}}+\gamma P_{\textcolor{blue}{{\pi_k^\prime}}}v_k)~~~~~~~~~~\textcolor{blue}{③}\\ &=\gamma P_{\pi_k^\prime}(v_{\pi_k}-v_k)\end{aligned} vπk+1−vk+1=(rπk+1+γPπk+1vπk+1)−πmax(rπ+γPπvk)≥(rπk+1+γPπk+1vπk)−πmax(rπ+γPπvk) ①=(rπk+1+γPπk+1vπk)−(rπk′+γPπk′vk) ②≥(rπk′+γPπk′vπk)−(rπk′+γPπk′vk) ③=γPπk′(vπk−vk)
因为 v π k − v k ≥ 0 v_{\pi_k}-v_k\geq0 vπk−vk≥0 且 P π k ′ P_{\pi_k^\prime} Pπk′ 非负。
则 γ P π k ′ ( v π k − v k ) ≥ 0 \gamma P_{\pi_k^\prime}(v_{\pi_k}-v_k)\geq0 γPπk′(vπk−vk)≥0
v π k + 1 − v k + 1 ≥ 0 v_{\pi_{k+1}}-v_{k+1}\geq0 vπk+1−vk+1≥0
归纳得到, 对任意
k
>
0
k > 0
k>0,
v
k
≤
v
π
k
≤
v
∗
v_k\leq v_{\pi_k}\leq v^*
vk≤vπk≤v∗。
而
v
k
v_k
vk 收敛到
v
∗
v^*
v∗, 由夹逼准则可得,
v
π
k
v_{\pi_k}
vπk 也收敛到
v
∗
v^*
v∗