最重要的连续分布的通用名是概率密度函数,而标准正态分布(Standard Normal Distribution) 是最重要的概率密度函数。这个连续分布之所以重要,我认为是因为它非常常见,换句话说,我们会很常用到它。标准正态分布(Standard Normal Distribution)的英文中的normal有正常,通用等意思,也就是说在生活中有很多东西都具有一般的、通用的模式,这个连续分布可以用来表达这种模式。正态分布,我将它理解为正常的常见的形态分布。
数据分布可以有多种形式,有的分布集中在左边,如:

有的数据会集中右边,如:
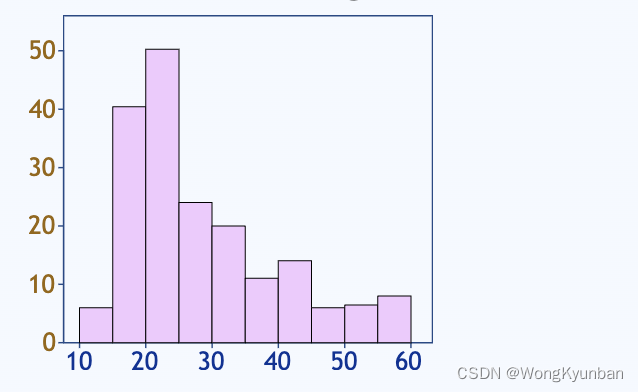
也有的数据分布得相对均匀,如:

在大多数数据分布中,许多情况下,数据往往围绕着一个中心值,没有左偏或右偏差,这种数据分布非常接近正态分布,这又再次说明正态分布的实用性和重要性。
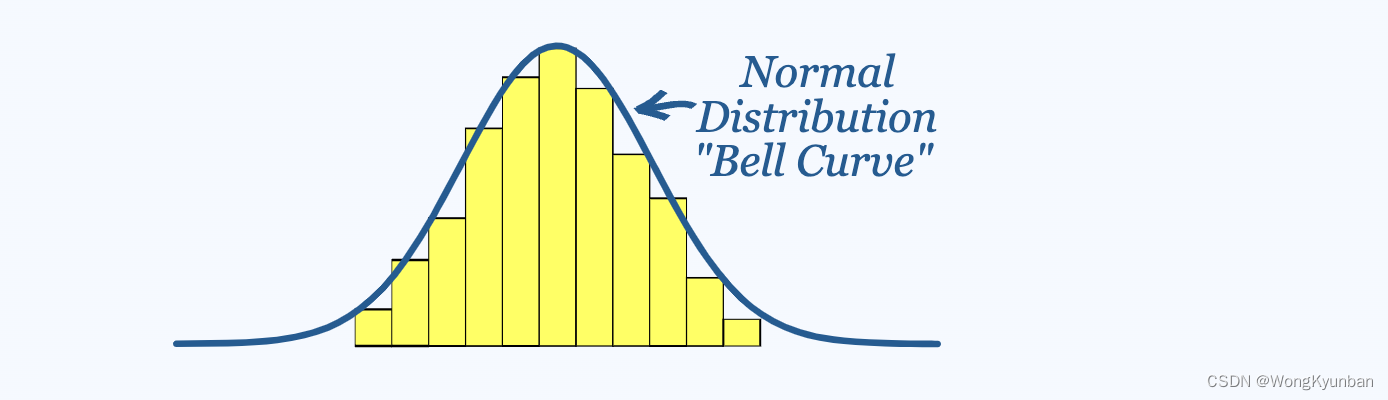
在上面这张图中,曲线代表的是正态分布,黄色的柱状图表示的数据很接近正态分布,用正态分布去近似的表示一些实际数据(很接近正态分布)是非常有价值的事情。
那么正态分布都有什么特点呢?
- 平均值 = 中位数 = 众数(mean = median = mode),这一大特点就说明了大多数据是围绕着一个中心值(这个中心值=平均值=中位数=众数)转的。
- 将正态分布用笛卡尔坐标(二维坐标)上表示出来,可以看到它是关于中心值对称的。
- 由第2点可知,有50%的数据小于或等于中心值,有50%的数据大于或等于中心值。
我们再来看看正态分布的标准差。什么是标准差呢?有什么用?标准差是衡量数字如何分布的指标。 简单地说就是每个数据离平均值的平均距离。如平均值是5,标准差是3,那么我们就知道在这些数据中,每个点与平均值的距离,平均是3那么远。
下面这些也是正态分布的一些重要特点:
σ :表示标准差,读sigma
μ:表示平均值 ,读mu
- 68%的数据落在 [μ-σ,μ+σ]
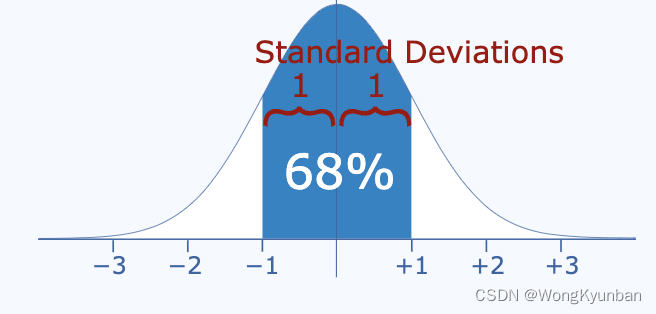
- 95%的数据落在[μ-2σ,μ+2σ]

- 99.7%的数据落在[μ-3σ,μ+3σ]
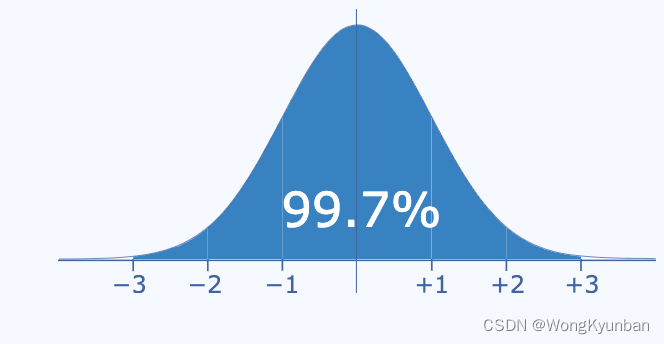
距离平均值多少个标准差(standard deviations),被称为"Standard Score"、“sigma(σ)” 、 “z-score”。
将一个数值转成一个Standard Score,只是就是计算这个数据离平均值有多少个标准差,计算方式如下:- 用这个数据减去平均值
- 然后除以标准差
上面这两个步骤就是正态分布转换成标准正态分布的过程。
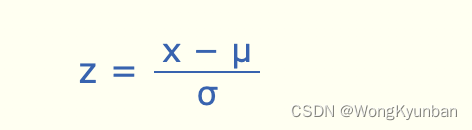
z :z-score,和Standard Score一个意思,只是正态分布有它自己一个更特别的叫法。
μ:平均值 (mu)
σ:表示标准差 (sigma)
x:要被标准化的值,如下文中的1.85
举个例子:
以下图是一个学校的学生的身高正态分布图,平均值、中位数、众数都是1.4,标准差是0.15(1.55-1.4 或1.7-1.55等等,因为正态分布是以标准差来划分区间的)如果有个学生的身高是1.85,那么他的Standard Score就是:
- 用1.85减去平均值: 1.85 - 1.4 = 0.45
- 然后除以标准差: 0.45 / 0.15 = 3
所以这个1.85的学生的Standard Score是3 。说明这个学生高出平均值3个标准差,
假如某个学生的身高是0.95,那么通过计算得到的Standard Score是-3,说明这个学生比平均值矮了3个标准差。
在这个例子的正态分布图中,平均值、中位数、众数都是1.4,说明这个学校的学生身高1.4的学生是居多的。

在刚刚上面这个例子中,我们将一些具体的数值转换成标准差的个数来表示,这就叫标准化。
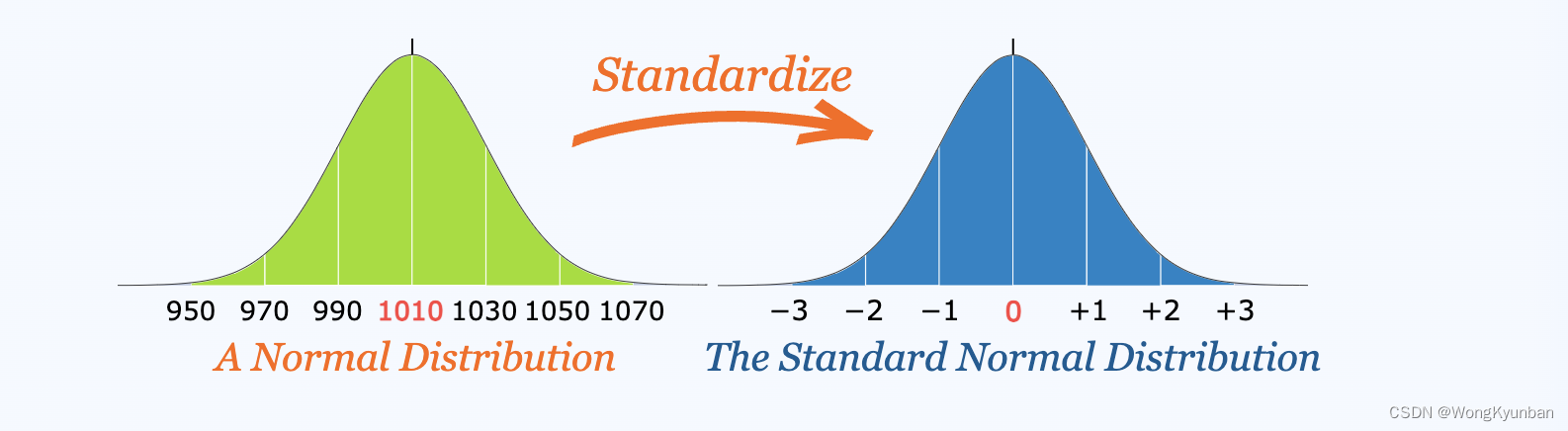
上图左边的图,用具体的值来表示分布,叫正态分布,把数值都转换成标准差个数来表示的正态分布图叫标准正态分布。我们可以将任何正态分布转化成标准正态分布。
为什么我们要做标准化呢?
其中一个最有说服力的理由就是可以帮助我们对数据做出决策。我从网上找来了这样一个例子来说明我们如何利用标准化对数据进行决策。
首先考试成绩的分布是符合正态分布的,否则我们没有理由去做正态分布来对数据进行相应的处理。话说在我第一次高中数学考试中,我们的成绩如下:
20, 15, 26, 32, 18, 28, 35, 14, 26, 22, 17
假设满分是60,那么我们在这次考试中大多数人都失败了。于是数学老师决定标准化这些分数,决定只有那些低于平均分一个标准差的同学都是不及格的。
通过计算可知,平均分(mean)为23,标准差(standard deviation)为6.6,标准化为每个同学的成绩的Standard scores(标准分)分别为):
-0.45, -1.21, 0.45, 1.36, -0.76, 0.76, 1.82, -1.36, 0.45, -0.15, -0.91
那么只有-1.21 和 -1.36是低于平均分1个标准差的,也就是说这次考试只有两人是不及格的。
上面就是利用标准化数据来对数据进行决策的一个例子了。
下面这张图显示了以0.5个标准差累积的百分比,只要符合正态分布,那么百分比的值都符合下图。

其实利用这张图我们还可以快速知道一些信息,比如说你已经知道你的考试成绩高于平均分0.5个标准差,
- 即[0,0.5]累知的百分比是19.1%,
- 小于平均分的百分比是50%
那么我们就知道理论上有69.1%(19.1%+50%)的同学的成绩低于你。虽然用真实数据来计算时,这个比值可能会有些差异。但是这种理论值已经很有价值了。
个人观点:其实近似的数据已经很能够给我们信息参考,帮助做决策,而至于非常具体的数值其实没有那么必要。
我找到了一个得用标准正态分布做生产决策的一个例子:有一家公司将盐包装在 1 公斤装的袋子中。生产部门抽样,称了一些样品的重量,得到了一些重量数据。
1007g, 1032g, 1002g, 983g, 1004g, …
他们计算平均值为1010g,标准差为20g。根据测量的数据,画了以下正态分布图。
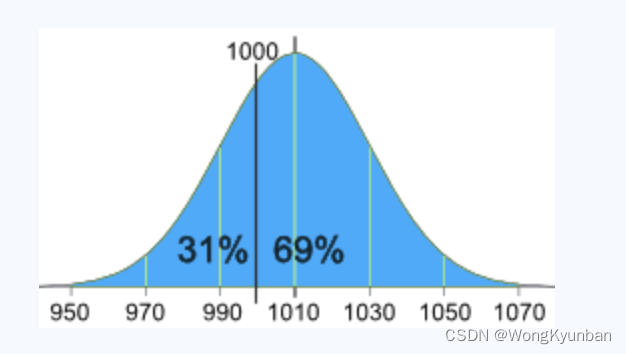
由上图我们可知,有31%袋子装了盐是小于1000g的。这是一个不好的信号,必须要改进。袋子装多少盐是一个很随机的事件,但是是有办法减少这种缺斤少两的情况的。
企业做了如下思考:
- 如果将1000g放在-3个标准差处,那就意味着只有0.1%甚至更少的袋子是装了少于1000g的,但是这可能有些困难的,几乎就是要保证100%的袋子都不小1000g
- 如果将1000g放在-2.5个标准差处,因为在3个标准差以外的部分占比约0.1%,3到2.5之间是0.5%,所以加在一起是0.6%。那就是说只有0.6%的袋子装了少于1000g的盐。
决定了要将1000g放在-2.5个标准差处,那么要怎样做才可以让数据按这个来分布呢(1000g在-2.5 Standard scores处)
- 增加每一袋子的盐量(这是通过改变平均值来实现的)
- 或者让每袋子的盐量装得更精确些(恰是1000g,这是通过减少标准差来实现的。)
方案一:如果是通过增加每一袋子的盐量,以此增大平均值,使用-2.5个标准差处是1000g,因为标准差是20g,所以需要2.5 x 20 = 50g,所以平均值是1050g才能保证-2.5个标准差处是1000g,调整过后的正态分布如下:

方案二:如果我们想保持当前的平均值1010g,那么我们可以通过减少标准差,也就是提高装盐量的精确度,-2.5个标准差处是1000g,与平均值1010g相差10g,10g/2.5=4g,即标准差为4g,就能够保证平均值(1010g)不变,同时使-2.5个标准差处是1000g。调整过后的正态分布如下:

方案三:当然我们也可以适当调高平均值,也适当减少标准差来实现。就是前两个方案的融合。