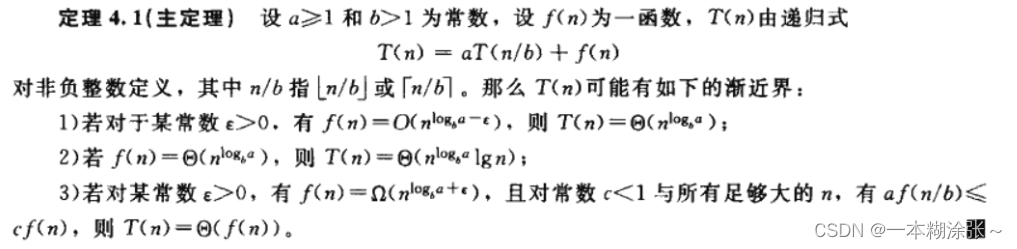渐进记号及时间复杂度计算
- 渐近符号
- 时间复杂度计算:递归方程
- 代入法
- 迭代法
- 套用公式法
渐近符号
渐近记号 Ω \Omega Ω
f
(
n
)
=
Ω
(
g
(
n
)
)
f(n)=\Omega(g(n))
f(n)=Ω(g(n)) 当且仅当存在正的常数C和
n
0
n_0
n0,使得对于所有的
n
≥
n
0
n≥ n_0
n≥n0 ,有
f
(
n
)
≥
C
(
g
(
n
)
)
f(n)≥C(g(n))
f(n)≥C(g(n))。此时,称
g
(
n
)
g(n)
g(n)是
f
(
n
)
f(n)
f(n)的下界。
根据符号
Ω
\Omega
Ω的定义,用它评估算法的复杂度得到的是问题规模充分大时的一个下界。这个下界的阶越高,评估越精确,越有价值。
例:设 f ( n ) = n 2 + n f(n)=n^2+n f(n)=n2+n,则
f ( n ) = Ω ( n 2 ) f(n)=\Omega(n^2) f(n)=Ω(n2),取 c = 1 , n 0 = 1 c=1,n_0=1 c=1,n0=1 即可
f ( n ) = Ω ( 100 n ) f(n)=\Omega(100n) f(n)=Ω(100n),取 c = 1 / 100 , n 0 = 1 c=1/100,n_0=1 c=1/100,n0=1 即可
显然, Ω ( n 2 ) \Omega(n^2) Ω(n2)作为下界更为精确。
渐进记号 Θ \Theta Θ
f
(
n
)
=
Θ
(
g
(
n
)
)
f(n)=\Theta(g(n))
f(n)=Θ(g(n)) 当且仅当存在正常数和
C
1
,
C
2
,
n
0
C_1,C_2,n_0
C1,C2,n0,使得对于所有的
n
≥
n
0
n≥n_0
n≥n0, 有
C
1
(
g
(
n
)
)
≤
f
(
n
)
≤
C
2
(
g
(
n
)
)
C_1(g(n))≤f(n)≤ C_2(g(n))
C1(g(n))≤f(n)≤C2(g(n))。此时,称
f
(
n
)
f(n)
f(n)与
g
(
n
)
g(n)
g(n)同阶。
这种渐进符号是指,当问题规模足够大的时候,算法的运行时间将主要取决于时间表达式的第一项,其它项的执行时间可以忽略不计。第一项的常数系数,随着n的增大,对算法的执行时间也变得不重要了。
例: 3 n + 2 = Θ ( n ) 3n+2= Θ(n) 3n+2=Θ(n)
10 n 2 + 4 n + 2 = Θ ( n 2 ) 10n^2+4n+2= Θ(n^2) 10n2+4n+2=Θ(n2)
5 × 2 n + n 2 = Θ ( 2 n ) 5×2^n+n^2= Θ(2^n) 5×2n+n2=Θ(2n)
渐进记号小 ο \omicron ο
f
(
n
)
=
ο
(
g
(
n
)
)
f(n)=\omicron(g(n))
f(n)=ο(g(n))当且仅当
f
(
n
)
=
ο
(
g
(
n
)
)
f(n)=\omicron(g(n))
f(n)=ο(g(n))和
g
(
n
)
≠
ο
(
f
(
n
)
)
g(n)\neq \omicron(f(n))
g(n)=ο(f(n)),此时,
g
(
n
)
g(n)
g(n)是
f
(
n
)
f(n)
f(n)的一个绝对上界。
小
ο
\omicron
ο提供的上界可能是渐近紧确的,也可能是非紧确的。(如:
2
n
2
=
ο
(
n
2
)
2n^2=\omicron(n^2)
2n2=ο(n2)是渐近紧确的,而
2
n
=
ο
(
n
2
)
2n=\omicron(n^2)
2n=ο(n2)是非紧确上界。
例: 4 n l o g n + 7 = ο ( n 2 ) 4nlogn + 7= \omicron(n^2) 4nlogn+7=ο(n2)
渐进记号小 ω \omega ω
f
(
n
)
=
ω
(
g
(
n
)
)
f(n)=\omega(g(n))
f(n)=ω(g(n))当且仅当
f
(
n
)
=
ω
(
g
(
n
)
)
f(n)=\omega(g(n))
f(n)=ω(g(n))和
g
(
n
)
≠
ω
(
f
(
n
)
)
g(n)\neq \omega(f(n))
g(n)=ω(f(n)),此时,
g
(
n
)
g(n)
g(n)是
f
(
n
)
f(n)
f(n)的一个绝对下界。
ω
\omega
ω表示一个非渐进紧确的下界。
例: f ( n ) = n 2 + n f(n)=n^2+n f(n)=n2+n,则 f ( n ) = f(n)= f(n)=\omega ( n ) (n) (n)是正确的, f ( n ) = f(n)= f(n)=\omega ( n 2 ) (n^2) (n2)是错误的。
渐进记号大 O \Omicron O
设
f
(
n
)
f(n)
f(n)和
g
(
n
)
g(n)
g(n) 是定义域为自然数集上的函数。若存在正数
c
c
c和
n
0
n_0
n0c和n_0c,使得对一切
n
≥
n
0
n≥ n_0
n≥n0 都有
0
≤
f
(
n
)
≤
c
g
(
n
)
0 ≤ f(n) ≤ cg(n)
0≤f(n)≤cg(n)成立,则称
f
(
n
)
f(n)
f(n)的渐进的上界是
g
(
n
)
g(n)
g(n),记作
f
(
n
)
=
O
g
(
n
)
f(n)=\Omicron g(n)
f(n)=Og(n)。
根据符号大
O
\Omicron
O的定义,用它评估算法的复杂度得到的只是问题规模充分大时的一个上界。这个上界的阶越低,评估越精确,越有价值。
例:设 f ( n ) = n 2 + n f(n)=n^2+n f(n)=n2+n,有
f ( n ) = O ( n 2 ) f(n)=\Omicron(n^2) f(n)=O(n2),取 c = 2 , n 0 = 1 c=2,n_0=1 c=2,n0=1即可
f ( n ) = O ( n 3 ) f(n)=\Omicron(n^3) f(n)=O(n3),取 c = 1 , n 0 = 2 c=1,n_0=2 c=1,n0=2即可
常见的时间复杂度关系
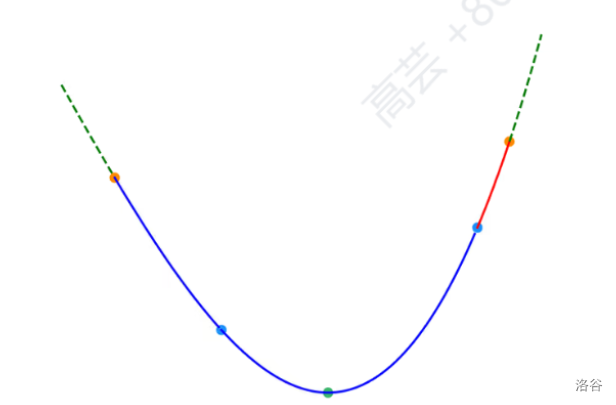
O(1)<O(log(n))<O(n)<O(nlogn)<O(n^{2})
O ( 2 n ) O(2^{n}) O(2n)和 O ( n ! ) O(n!) O(n!)大于以上的所有时间复杂度,具体原因参考图像。
时间复杂度计算:递归方程
加、减、乘、除、比较、赋值等操作,一般被看作是基本操作,并约定所用的时间都是一个单位时间;通过计算这些操作分别执行了多少次来确定程序总的执行步数。一般来说,算法中关键操作的执行次数决定了算法的时间复杂度。
比较简单的算法时间复杂性估计通常需要观察在for、while循环中的关键操作执行次数,在这里我们只讨论一种比较复杂的时间复杂度计算问题:求递归方程解的渐近阶的方法。递归式就是一个等式,代表了递归算法运算时间和n的关系,通过更小输入的函数值来描述一个函数。那么如何求得递归算法的Θ渐进界呢?主要有三种方法。
代入法
代入法是指自己猜测一个界,然后用数学归纳法进行验证是否正确,这种猜测主要靠经验,不常用。
迭代法
迭代法是指循环地展开递归方程,然后把递归方程转化为和式,使用求和技术解之。
套用公式法
这个方法为估计形如:
T
(
n
)
=
a
T
(
n
/
b
)
+
f
(
n
)
T(n)=aT(n/b)+f(n)
T(n)=aT(n/b)+f(n) 的递归方程解的渐近阶提供三个可套用的公式。要求其中的a≥1和b>1是常数,f(n)是一个确定的正函数。那么在三种情况下,我们可以得到T(n)的渐进估计式,懒得打公式,所以截图。