二分 & 分治

---

二分

二分查找

也叫折半搜索，用于在一个有序数组中查找某一元素的算法。

给定一个长度为 $n$ 的从小到大排列的数列 $a$ 和 $q$ 次询问，每次询问给定 $x$，查找 $x$​ 在数列中的位置。

$n,q\le 10^6$。

对于 $a_i$，如果 $x<a_i$，因为 $a$ 有序，则 $x<a_{[i,n]}$；同理如果 $x>a_i$，则 $x>a_{[1,i]}$。然后就可以二分了。令 $[l,r]$ 表示 $x$ 可能的区间，每轮求出一个 $mid=\frac{l+r}{2}$，如果 $x=a_{mid}$ 则 $mid$ 即为答案；如果 $x<a_{mid}$ 则区间被缩短为 $[l,mid-1]$；否则区间被缩短为 $[mid+1,r]$。每一轮使答案区间减半，所以单词查询复杂度为 $O(\log n)$。

int Query(int x) {
    int l = 1, r = n, mid
    while (l <= r) {
		mid = l + r >> 1; // >> 1 与 / 2 基本等价
        if (a[mid] == x) return mid;
        if (x < a[mid]) r = mid - 1;
        else l = mid + 1;
    }
    return -1;
}

可以直接使用 STL 中的两个二分查找函数：

upper_bound(a + 1,a + n + 1,x); // 返回数组中第一个大于 x 的数的地址，如果需要下标则要减去 a
lower_bound(a + 1,a + n + 1,x); // 返回数组中第一个不小于 x 的数的地址
// 如果没有结果则返回 end()

要求传入的数组 $a$ 有序。

共有两个人，规定一场比赛共有 $s$ 局，每一局中先得到 $t$ 分的人获得这一局的胜利。现在按照时间给定这两人的得分情况，但不知道是第几局得到的第几分，只知道是谁得到的分。求所有可能的 $(s,t)$，保证得分情况是完整的。

当其中一人得到 $t$ 分时，一局就会结束，所以一局中两人一共最多得 $2t-1$ 分，最少得 $t$ 分。所以考虑前缀和，预处理出两个人在任意时间段分别得的分，然后若干轮二分将得分情况切分成若干局。假设上一轮二分将这一局的得分情况起点推到了 $L$，则本轮二分的答案区间即为 $[L+t,L+2t-1]$；对于二分中得到的某个 $mid$：

• 如果在 $[L,mid]$ 中，其中一人得到了 $t$ 分，另一个得到了 $t$ 分一下，则 $mid$ 即为本局终点；
• 如果在 $[L,mid]$ 中，其中一个得到超过 $t$ 分或两人都得到了 $t$ 分，说明 $mid$ 太靠后了，二分区间变更为 $[l,mid-1]$；
• 否则说明 $mid$ 太靠前了，二分区间变更为 $[mid+1,r]$。

最终判断是否所有得分情况都被一局包含即可。复杂度 $O(n{\log }^{2}n)$，$n$ 为得分情况总数。

二分答案

针对于答案具有单调性的题目。即如果答案为 $x$ 成立，那么比 $x$ 更宽松的也成立；如果 $x$ 不合法，那么比 $x$ 更苛刻的也不合法。所以考虑枚举答案判断是否成立，类似于二分查找，也有一个答案区间 $[l,r]$，判断 $mid$ 是否合法时需要一个 check 函数。意义即为：花费一个 $\log n$ 的时间复杂度，将求答案转换为判断答案是否合法。如果题目中的答案明显具有单调性，或者要求最大值最小/最小值最大。check 函数通常和贪心算法或一些数据结构配合使用。

P2678 [NOIP2015 提高组] 跳石头

题目中 最短跳跃距离尽可能长 提示使用二分答案，即二分这个最短跳跃距离。对于二分值 $x$，check 中枚举相邻石头，如果发现两者距离小于 $x$，则说明需要移走一块石头。判断移走石头的数量是否小于 $M$ 即可。细节部分不作赘述。

有一条数轴和 $n$ 个人，第 $i$ 个人的移动速度为 $v_i$，位置为 $x_i$​。现在要求选定一个集合点，使得最后一个到这个点的人所花费时间最小。求这个最小时间。

也是二分这个时间。对于时间 $t$，第 $i$ 个人的活动范围即为 $[x_i-v_i\times t,x_i+v_i\times t]$。最后看 $n$ 个人的活动范围是否存在交集即可。可以开 $L,R$ 两个变量表示当前交集的左右端点，$O(n)$ 扫一遍更新，最后看 $L\le R$ 是否成立即可。

P4409 [ZJOI2006] 皇帝的烦恼

$50\%$ 左右做法：求 max ⁡ { a i + a i + 1 } \max\{a_i+a_{i+1}\} max{ai​+ai+1​} 即可，只适用于 $n$ 为偶数的情况。其实加一小句话，这个做法也能 AC。

$100\%$ 做法：二分勋章数，令 $f_i$ 表示第 $i$ 个人在不与 $i-1$ 冲突的情况下，$i$ 与 $1$ 的最小冲突量；$g_i$ 表示不与 $i-1$ 冲突时与 $1$ 的最大冲突量。假设二分到勋章数为 $m$，则转移方程即为：
$$f_i=\min (a_i,a_1-g_{i-1}),g_i=\max (0,a_i-(m-a_1-a_{a-1})-f_{i-1})$$
可以对着方程推一下，$m$ 合法的条件即为 $g_n=0$。

分治

顾名思义，将问题分成几个子问题，然后通过子问题的解合并出该问题的解。而对于长度为 $1$ 等规模很小的子问题则直接解决。通常使用递归解决。

归并排序，$\text{merge\_sort}$

对于分治区间 $[L,R]$，使得 $[L,R]$ 中的元素有序。如果 $L=R$ 则直接返回，否则将当前序列平分成左右两半分治解决，然后将左右两个有序合并。具体地，不断从两个有序序列首部取较小值放入答案序列即可。

快速排序，$\text{quick\_sort}$

区别在于每次从 $[L,R]$ 中随机选出一个元素作为基准，将比它小的元素排到左边，比它大的排到右边，然后再递归处理左右序列。最坏情况是 $O(n^2)$ 的。

P7883 平面最近点对（加强加强版）

以 $x$ 坐标排序，考虑按 $x$ 坐标分治。每次取中间的点将剩余点集分为规模相等的两部分，递归求出左右两侧的点对最近距离，记为 $ansL,ansR$。则当前区间 $[L,R]$ 中的答案 $ans$ 一定不大于 $\min (ansL,ansR)$。将 $\min (ansL,ansR)$ 距离内的点按照 $y$ 坐标排序（可以在分治过程中归并排序），对于每个左侧点，只需要考虑右侧宽 $\min (ansL,ansR)$、高 $2\times \min (ansL,ansR)$​ 的矩形范围内的点，与其进行配对。

时间复杂度接近 $O(n\log n)$。

杂项

浮点数二分

for (int st = 0;st < 100;st ++) { // 控制二分次数
	double mid = (l + r) / 2;
    if (check(mid)) r = mid;
    else l = mid;
} // 最终答案为 r

三分

用于求单峰函数的极值点，通常使用二分法衍生出的三分法。对于这个函数图像：

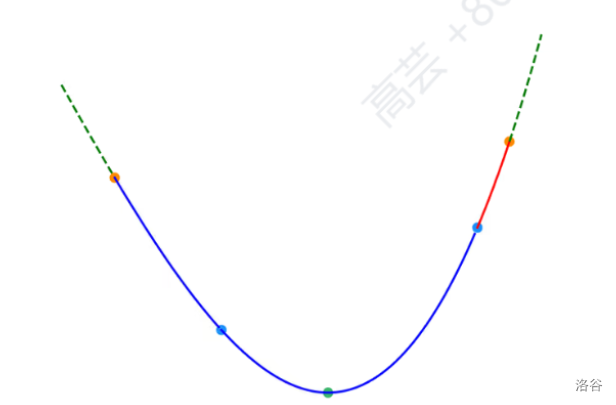
基本逻辑类似，假设 $x$ 的函数值为 $f(x)$，对于当前区间 $[L,R]$（红点之间的部分），我们在区间内任取两点 $mL,mR(mL<mR)$（两个蓝色的点）；如果 $f(mL)<f(mR)$​，则在 $[mR,R]$（红色部分）中函数值必然单调递增，最值（绿点）必然不在这一区间。每一轮都会舍去两侧区间中的其中一个。为减少三分的次数，可以让 $mL\leftarrow mid-\text{eps},mR\leftarrow mid+\text{eps}$，其中 $\text{eps}$ 为一个很小的值。复杂度和 ${\log }_{2}n$ 十分接近。

while (r - l > eps) {
    mid = (lmid + rmid) / 2;
    lmid = mid - eps, rmid = mid + eps;
    if (f(lmid) < f(rmid)) r = mid;
    else l = mid;
}

分数规划

用来求一个形如
$$\frac{{\sum }_{i=1}^n{a}_i\times w_i}{{\sum }_{i=1}^n{b}_i\times w_i}$$
的分式的极值，其中 w i ∈ { 0 , 1 } w_i\in\{0,1\} wi​∈{0,1} 且会受到约束（比如说最多 $n-1$ 个 $w_i$ 能取 $1$ 等）。考虑二分这个极值 $mid$，即使得
$$\frac{{\sum }_{i=1}^n{a}_i\times w_i}{{\sum }_{i=1}^n{b}_i\times w_i}>mid$$
变换一下可得
$$\sum _{i=1}^n{w}_i\times (a_i-mid\times b_i)>0$$
所以 check 部分需要使得值为正。具体怎么选取 $w_i$ 依据题目而定。

给定一张图，第 $i$ 条边的边权为 $w_i$，求在原图中找一个环使得环上的边边权之和，与环的大小的比值最小。

根据得到的式子，把 $a_i-mid\times b_i$ 作为每条边的新边权，然后看图中是否存在负环即可。

下午题

Desert King

每条边有两个权值 $a_i$ 和 $b_i$，求一棵生成树 $T$ 使得树上边权 $a$ 之和与 $b$ 之和的比值最小。

类似的，把 $a_i-mid\times b_i$ 作为每条边的新边权，然后检查最小生成树是否大于 $0$ 即可。注意这题时限卡的很紧，且没有 bits/stdc++.h 这个库可以用。

Rest In The Shades

考虑连接点 $P$ 和 $A,B$，交 $x$ 轴（即栅栏所在的直线）于两点 $A^{\prime },B^{\prime }$。算出 $A^{\prime },B^{\prime }$ 中栅栏的占比，此时 $A,B$ 中产生阴影的距离就可以通过相似三角形求出。可以两遍二分求出 $A^{\prime },B^{\prime }$ 附近的线段，最后前缀和统计阴影总长度即可。

The Hidden Pair (Hard Version)

询问次数不能超过 $11$ 次，这个数字与 $\log n$ 的值很接近。考虑先对所有 $n$ 个点进行询问，这样就可以得到 $X,Y$ 之间的距离，和一个必定在 $X,Y$ 路径上的点。设这个点为 $rt$，$X,Y$ 之间的距离为 $dis$。如果我们以 $rt$ 为树根，那么对于树中深度为 $dep$ 的点集 { A } \{A\} {A}，且 $dep$ 大于等于 $X,Y$ 中较小的深度，我们对其进行询问：

• 如果询问得到的距离和为 $dis$，则表示询问得到的点在 $X,Y$ 的路径上，即 $X,Y$ 中较大的深度大于等于 $dep$；
• 如果询问得到的距离和大于 $dis$，则表示该深度的点中没有在 $X,Y$ 的路径上的，即 $X,Y$ 中较大深度小于 $dep$。

对于第一种情况询问到的点都可能是 $X,Y$ 中深度较大的点，不妨令 $de{p}_X\ge de{p}_Y$。考虑二分，区间为 $[\lfloor \frac{dis}{2}\rfloor ,\min (dis,Dep)]$，其中 $Dep$ 为最大深度。每一轮都询问一次深度为 $mid$ 的点集，按照上述两种情况二分，最终可以得到深度较大的 $X$。然后我们以 $X$ 为树根，然后询问深度为 $dis$ 的点集，得到的点即为 $Y$。