为了解决特定问题而进行的学习是提高效率的最佳途径。这种方法能够使我们专注于最相关的知识和技能，从而更快地掌握解决问题所需的能力。

（以下练习题来源于《统计学—基于Python》。联系获取完整数据和Python源代码文件。）

---

练习题

为了分析影响不良贷款的因素，一家商业银行在所属的多家分行中随机抽取25家，得到的不良贷款、贷款余额、应收贷款、贷款项目个数、固定资产投资等有关数据如下（前3行和后3行）。

不良贷款	贷款余额	应收贷款	贷款项目个数	固定资产投资
0.9	67.3	6.8	5	51.9
1.1	111.3	19.8	16	90.9
4.8	173	7.7	17	73.7
...	...	...	...	...
1.2	109.6	10.3	14	67.9
7.2	196.2	15.8	16	39.7
3.2	102.2	12	10	97.1

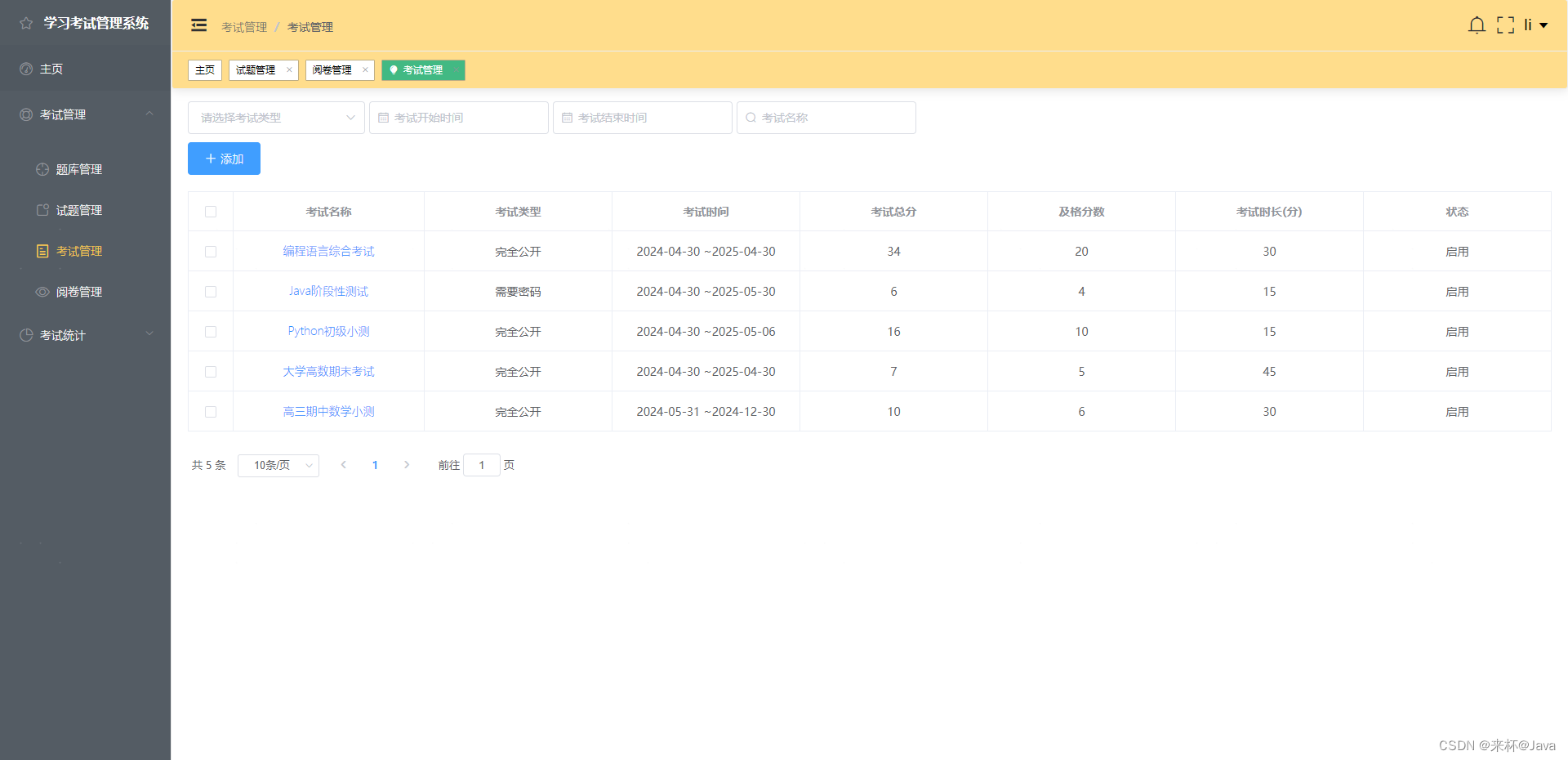
（1）用不良贷款作为因变量，建立多元线性回归模型。

（2）分析模型中是否存在共线性。

（3）比较4个自变量在不良贷款中的相对重要性。

---

计算结果与分析

（1）用不良贷款作为因变量，建立多元回归模型，结果如下图所示。

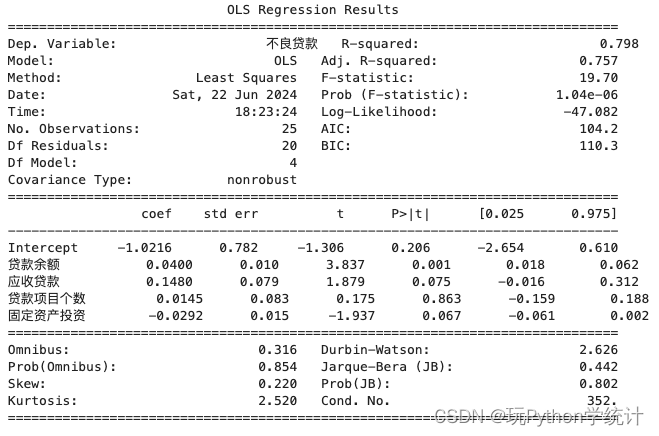
# 拟合多元线性回归模型
from statsmodels.formula.api import ols
import pandas as pd
df = pd.read_csv('exercise10_3.csv')

model_m = ols('不良贷款 ~ 贷款余额+应收贷款+贷款项目个数+固定资产投资', data = df).fit()
print(model_m.summary())

（2）计算VIF与容忍度判断分析模型中是否存在共线性。计算结果如下，VIF和容忍度显示，共线性均在可接受的范围内。

import pandas as pd
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor

# 读取数据
df = pd.read_csv('exercise10_3.csv')

# 选择自变量列
X = df[['贷款余额', '应收贷款', '贷款项目个数', '固定资产投资']]

# 添加常数项
X = sm.add_constant(X)

# 计算VIF
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]

# 计算容忍度
vif_data["tolerance"] = 1 / vif_data["VIF"]

print(vif_data)

（3）计算标准化回归系数，比较 4 个自变量在不良贷款中的相对重要性。结果如下图所示。按标准化回归系数的绝对值大小排序为贷款余额最大，其次是固定资产投资、应收贷款和贷款项目个数。因此，在4个自变量中，贷款余额是影响不良贷款最重要的变量。

# 计算标准化回归系数，比较 4 个自变量在不良贷款中的相对重要性
import pandas as pd
from statsmodels.formula.api import ols
from scipy import stats
df = pd.read_csv('exercise10_3.csv')

z = stats.zscore(df, ddof = 1)  # 数据框标准化
df_z = pd.DataFrame(z, columns = ['不良贷款', '贷款余额', '应收贷款', '贷款项目个数', '固定资产投资']) # 将数组转换成数据框并重新命名为df
model_z = ols('不良贷款 ~ 贷款余额+应收贷款+贷款项目个数+固定资产投资', data = df_z).fit()
print(model_z.summary())

---

都读到这里了，不妨关注、点赞一下吧！