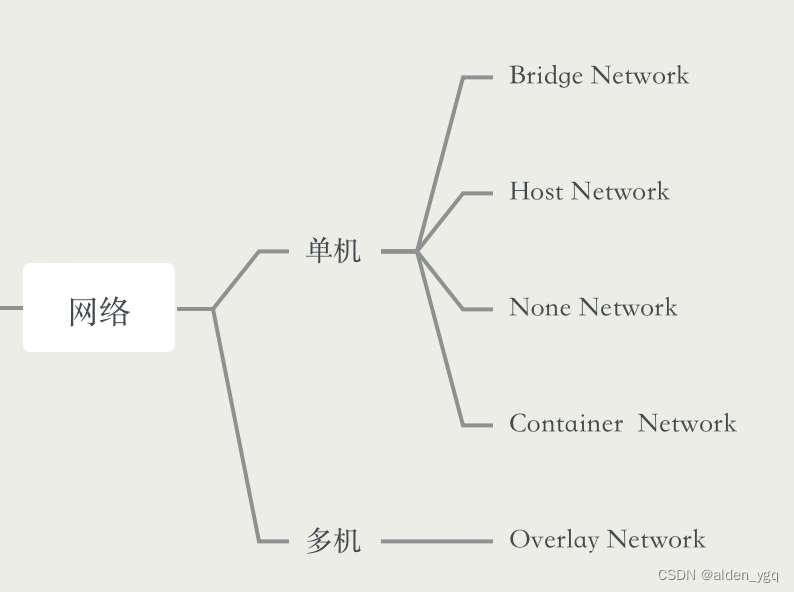
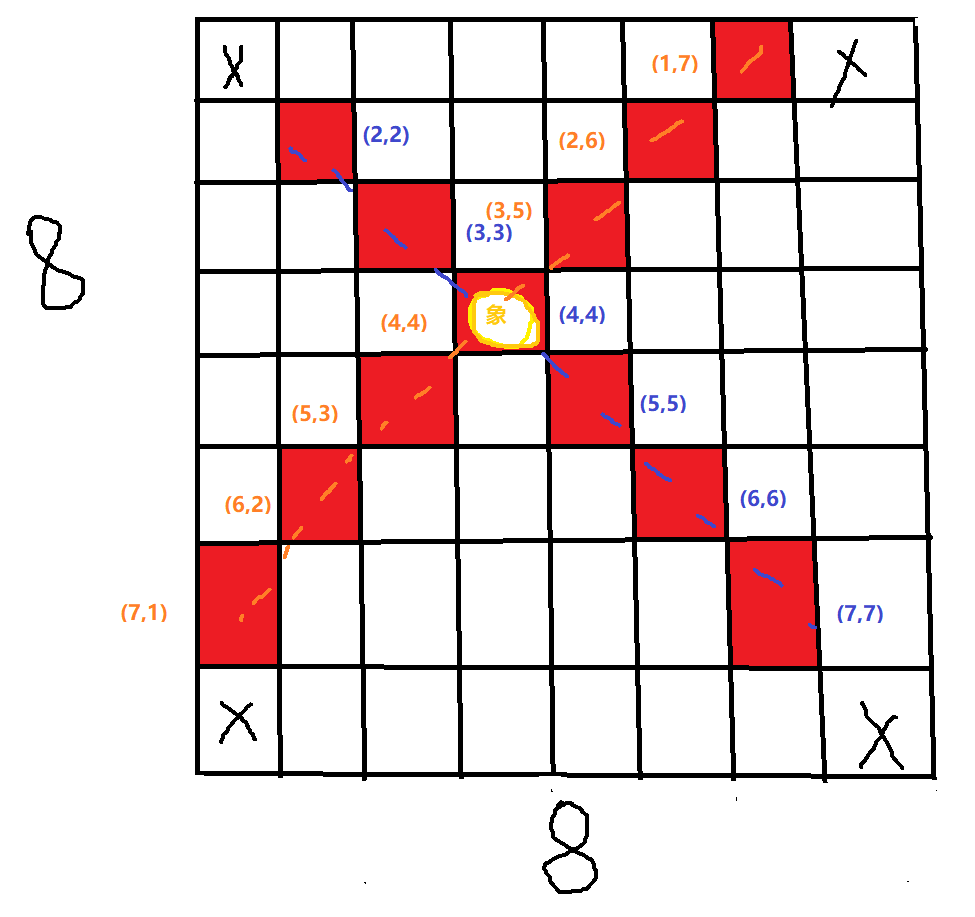
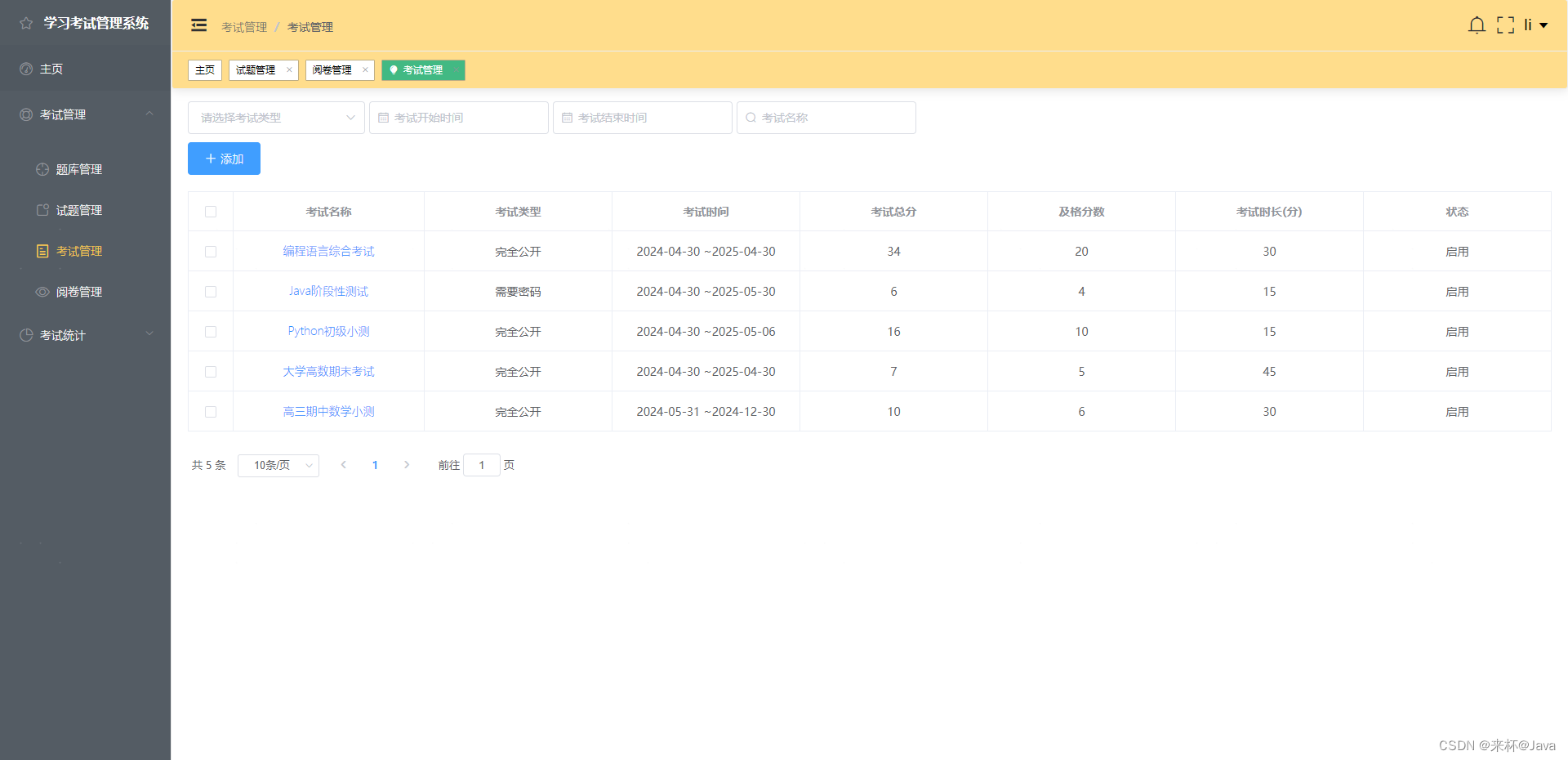
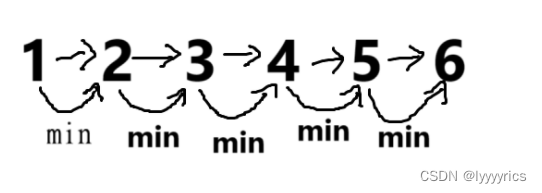
顺序查找
查找数组a中第一次出现数字m的下标，并输出该下标；
如果没有则输出sorry。
1 定义变量 数组a，n表示数组的个数， m要查找的数字
2 用sizeof()函数，求出数组元素的个数
3 从键盘中任意输出一个数字m，进行查找
4 for循环，遍历数组，一一比较是否是m
  找到了m，输出其下标
5 遍历完整个数组，都没有找到m,输出sorry。

【运行结果】

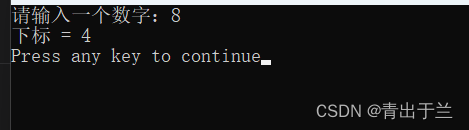
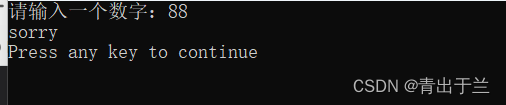
【程序代码】

#include <stdio.h>

int main(void)
{
    int a[] = {12, 19, 48, 56, 8, 567, 23, 57, 99, 4, 78, 66};
    int n; //存放数组a中元素的个数
    int m; //查找的数字
    int i; //循环变量

    n = sizeof(a) / sizeof(int); //求出数组中所有元素的个数
    
    printf("请输入一个数字：");
    scanf("%d", &m);
    for(i=0; i<n; i++)
    {
        if(a[i] == m)
        {
            printf("下标 = %d\n", i);
            break;
        }
    }

    if(i == n)
    {
        printf("sorry\n");
    }

    return 0;
}