文章目录
- 什么是最短路问题?
- 1.迷宫中离入口最近的出口
- 2.最小基因变化
- 3.单词接龙
- 4.为高尔夫比赛砍树
- 总结

什么是最短路问题?
最短路问题是图论中的经典问题,旨在寻找图中两个节点之间的最短路径。常见的最短路算法有多种,这次我们讲的主要是以边权为1的最短路问题,什么是边呢?在图论中,权是两个节点的连线的路程。
举个简单的例子:

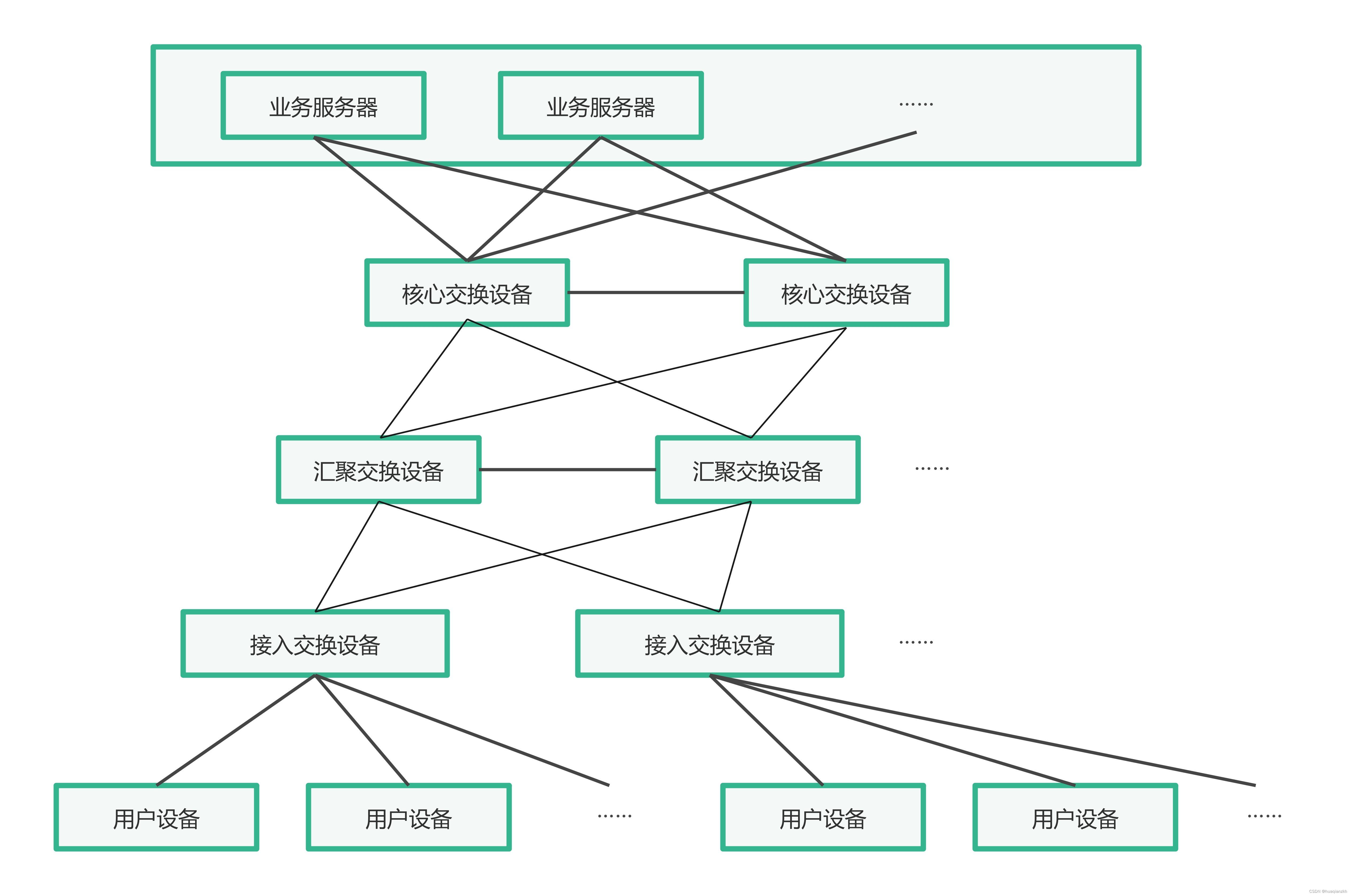
下面这个图求A->H的最短路,很明显最短路就是A->E->G->H。
那我们该如何求出这个最短路呢?
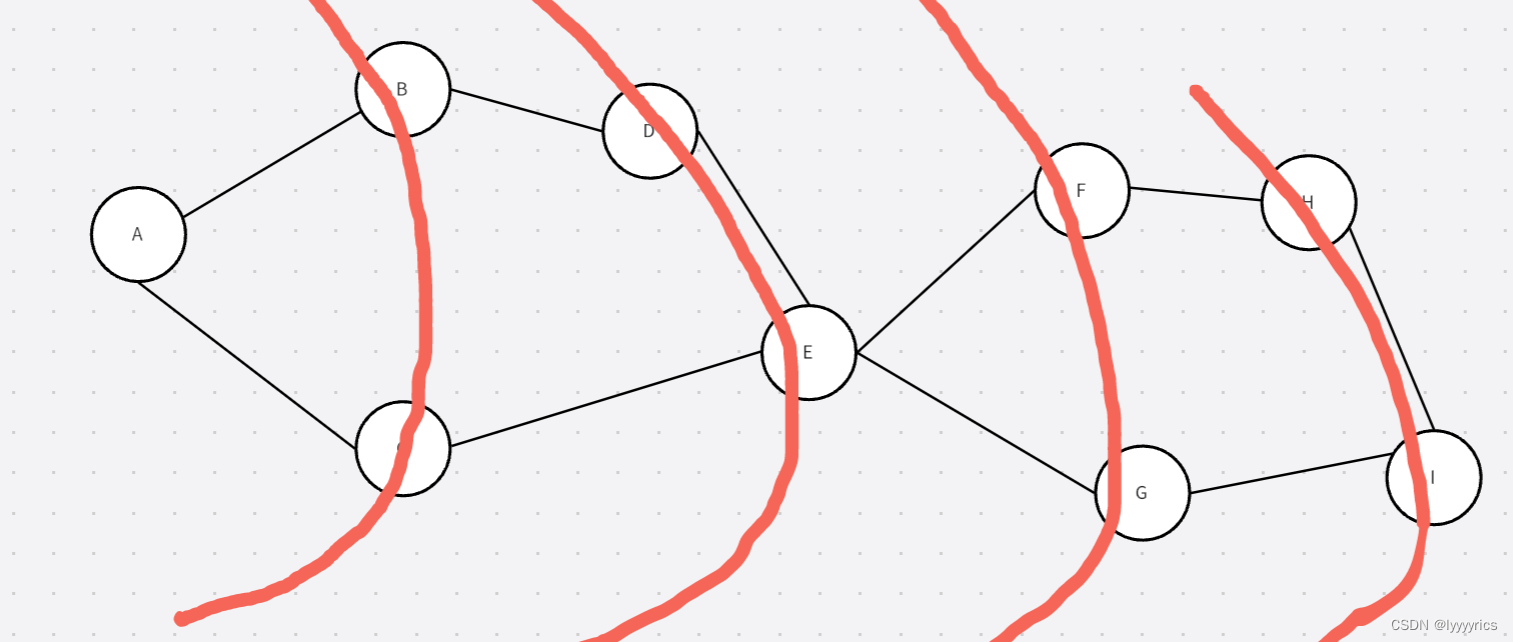
我们可以先将A入进一个队列中,然后将A取出来,将与A相连的两个节点也一起入进去,然后这两个必须一起出队列,这里一起出,并不是同时出而是在一趟中一起出,然后依次循环这个过程,直到找到最后一个节点I,可以看见,最短路的距离其实和入的层数是一样的。这就是我们找到的规律,后面做题需要用到。
接下来我们展示几道例题来更好的理解这个问题:
1.迷宫中离入口最近的出口
题目链接
题目:
样例输入和输出:
这道题的意思很简单,题目给我们一个迷宫,这个迷宫是二维数组,二维数组中存放+就表示是障碍,存放.就表示是路,这里的问题是,先给我们一个起始坐标,然后让我们找到最近的出口,这里出口就是边界位置的.,但是有一种情况,当起始位置是边界位置的时候时,这个出口不能被当做出口。问题就是让我们求出到达出口的最短路,就是转化为找到里起始位置最近的.且起始位置不在边界位置的出口。
接下来题目弄懂了,我们来考虑一下算法该怎么做。
算法原理:BFS
这里我们需要一个队列,这个队列存储路的位置,还需要一个vis二维数组,用来标记当前位置已经被走过了,注意这里我们用的广度优先搜索,所以按照上面的图我们应该同时把初始位置的左边位置和上面位置同时入到队列当中,然后pop的时候也要一起pop,做到一层一层的入,我们画个图演示一下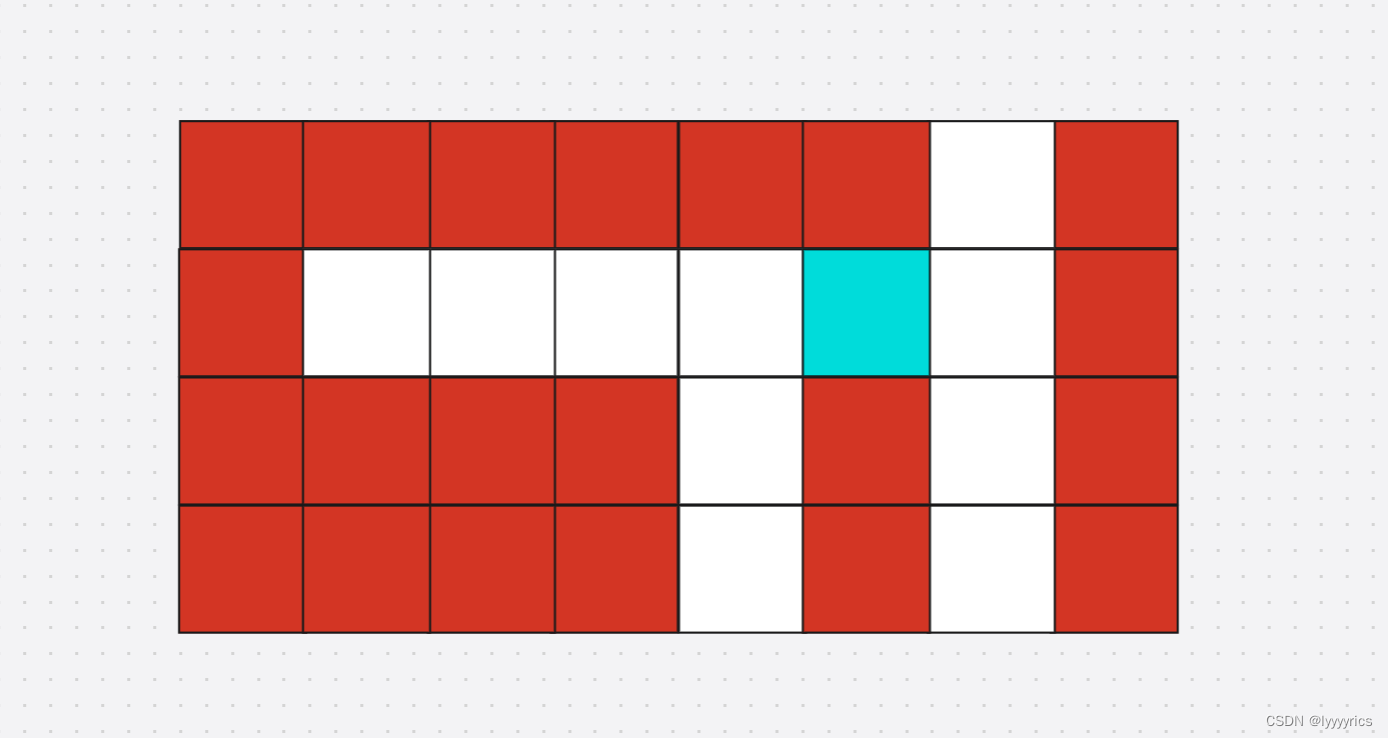
蓝色表示起点。
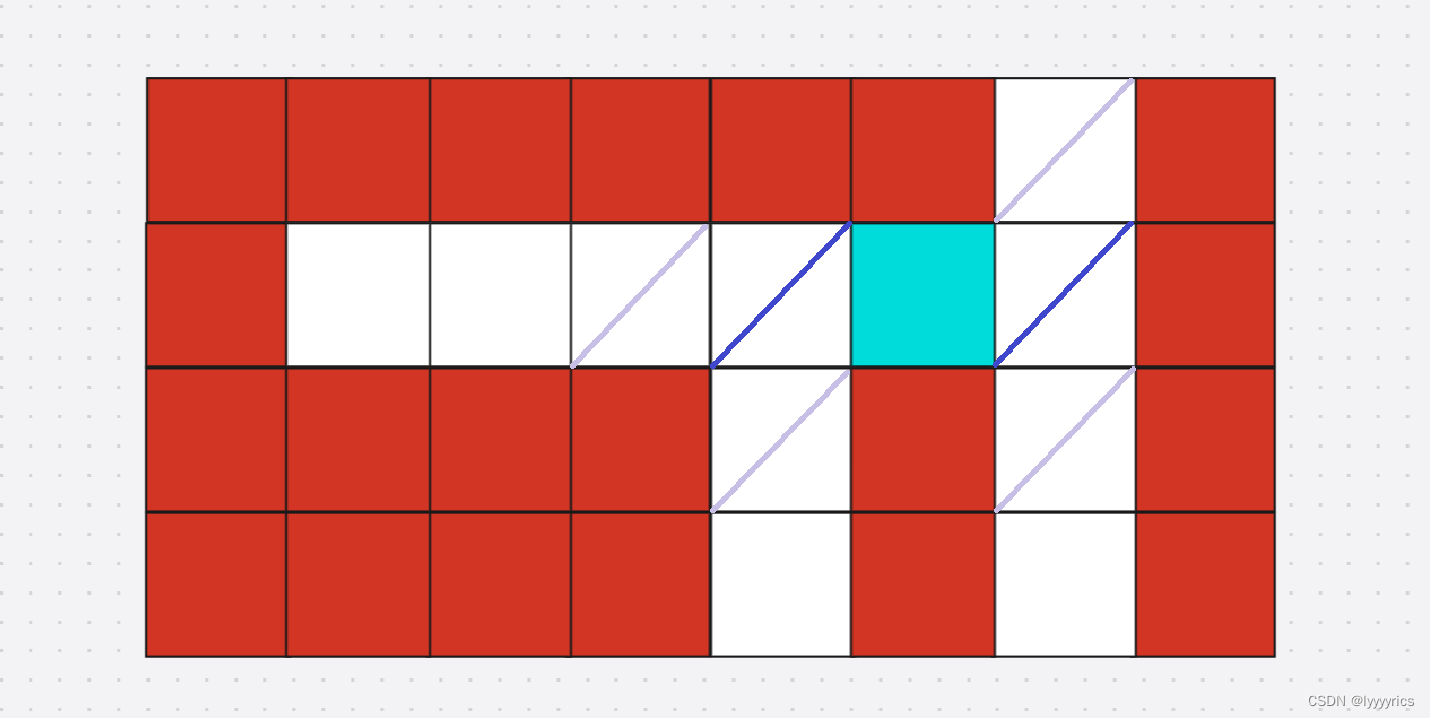
很显然,第一次我们将初始节点入进队列,然后第二次同时将深蓝色标记的节点入进队列,第三次将深蓝色标记的节点的相邻的节点入进队列,就找到了,我们一共入了两次,将初始节点给除掉,所以这里最短路是2。
代码展示:
class Solution {
public:
bool vis[101][101];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
typedef pair<int,int> PII;
int m,n;
int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
m=maze.size();
n=maze[0].size();
queue<PII> q;
q.push({entrance[0],entrance[1]});
vis[entrance[0]][entrance[1]]=true;
int step=0;
while(q.size())
{
step++;
int sz=q.size();
for(int i=0;i<sz;i++)
{
auto [a,b]=q.front();
q.pop();
for(int k=0;k<4;k++)
{
int x=a+dx[k];
int y=b+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&maze[x][y]=='.'&&vis[x][y]==false)
{
//判断是否走到了终点
if(x==0||x==m-1||y==0||y==n-1)
{
return step;
}
q.push({x,y});
vis[x][y]=true;
}
}
}
}
return -1;
}
};
2.最小基因变化
题目链接
题目:
样例输入和输出:
最小基因变化这道题,我最开始做的时候也不能将这道题和最短路联系起来,但是这道题确实可以转化为最短路问题,这道题就类似于决策树,首先我们看题意,这道题给我们一个基因序列,则合格序列是由一个八个字符的字符串所构成,这道题给我们一个初始基因序列,给我们一个需要让我们经过变化得到的基因序列,但是这道题并不是让我们直接变化,这道题还给我们一个基因库,我们每次基因序列的变化后的基因序列必须存在于基因库中,这个变化才是有效变化,否则这个变化是无效变化。
接下来我们来举个例子:
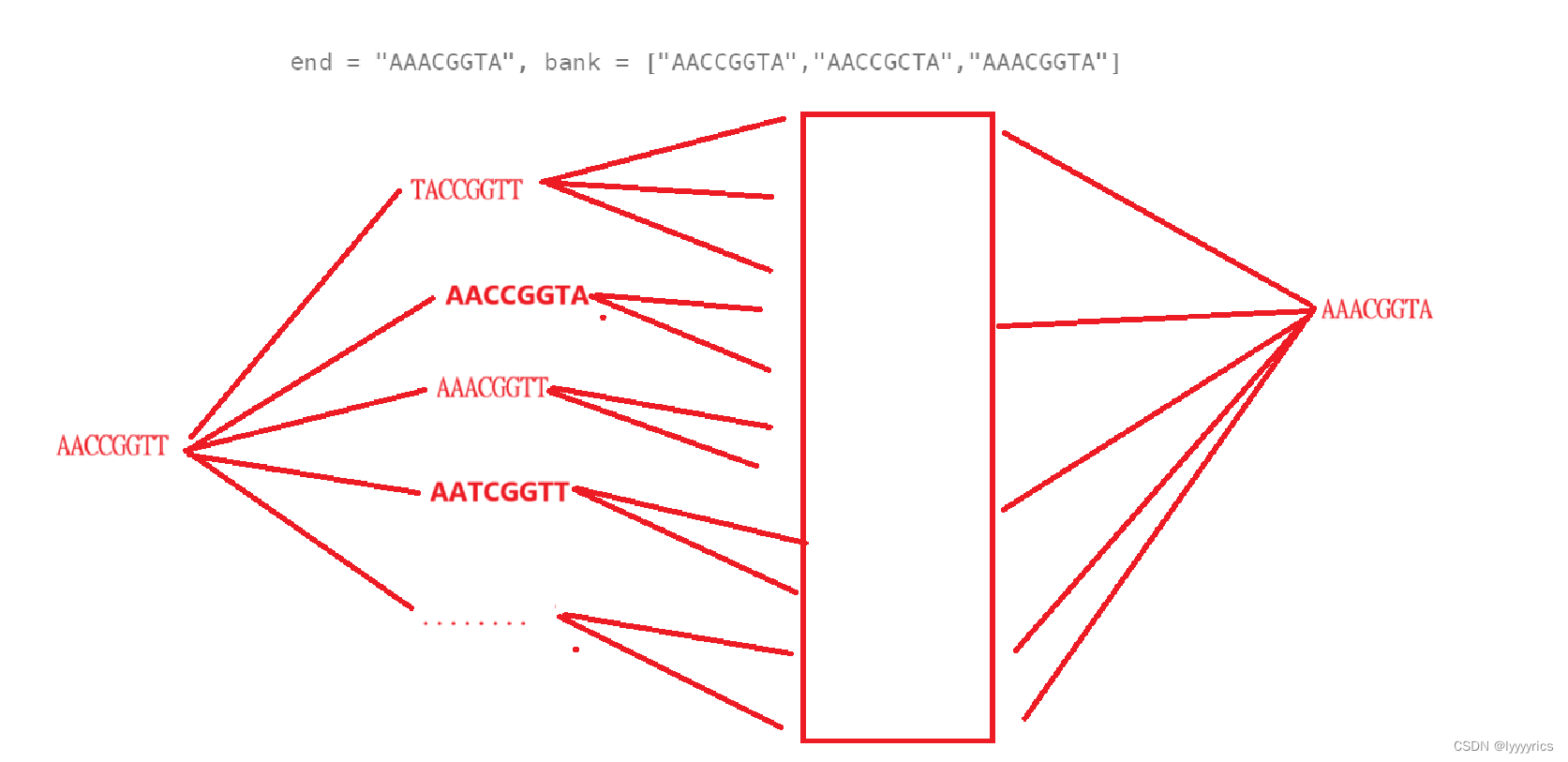
我们用方框表示很多次变化过后,最后变成了我们的最终需要的基因序列,可以看见最开始给我们的初始的基因序列,可以通向很多个基因序列,但是不是每个基因序列我们都是需要的,我们需要在基因库中查找这个变化后的序列是否存在,最后经过很多次变化过后我们得到了最终我们需要的基因序列,我们需要返回的是什么呢?返回我们变化的最少次数。
算法原理:
这道题很显然也可以转化为最短路问题,这道题我们也需要一个队列,然后先用一个hash表将基因库存起来,然后将初始的基因序列入队列,然后我们再开一个hash表,将这个基因序列插入到hash表中标记一下,表示这种变化状态我们已经经历过了。我们还需要把这个字符串的每个位置遍历一遍,因为一次变化一次,有很多种情况,所以我们需要把每个情况遍历一遍,基因序列的每个位置的变化状态我们都必须知道,如果这个状态是满足在基因库中的,我们就入队列,==注意:我们是一层一层的入,第一次变化属于一层,我们需要把所有都在基因库中的存在的状态都入到队列中,顺便标记一下这种状态已经经历过了。然后每次遍历一层之后我们都需要对一个变化次数的变量++,最后这个变化次数就是最小的变化次数。
代码展示:
class Solution
{
public:
int minMutation(string startGene, string endGene, vector<string>& bank)
{
//hash1负责存储访问过的有效基因
unordered_set<string> hash1;
//hash2负责存储基因库中的基因序列
unordered_set<string> hash2(bank.begin(), bank.end());
//方便直接遍历的时候用来修改基因序列
string change = "ACGT";
//当start和end还没遍历就相等时,直接返回0
if (startGene == endGene)return 0;
//当在hash2中没有找到end的时候也不需要遍历,因为最后的结果没有在基因库中
if (!hash2.count(endGene))return -1;
//队列存储基因序列
queue<string> q;
//先插入一个基因序列
q.push(startGene);
//标记这个基因序列已经被访问过了
hash1.insert(startGene);
//记录每次操作的步骤
int ret = 0;
while (q.size())
{
//先将ret++
ret++;
int sz = q.size();//每次一层一层的出
while (sz--)
{
//用一个临时变量来存储front
string tmp = q.front();
//将队头的变量pop掉
q.pop();
//遍历每一种可能出现的情况
for (int i = 0;i < 8;i++)
{
//如果我们这里每次修改的是tmp的话,第二次我们用的是上次修改过的tmp进行操作,所以这里开一个
//临时的string进行操作,每次只进行一次操作
string t = tmp;
for (int j = 0;j < 4;j++)
{
t[i] = change[j];//改变单个字符
//判断是否在基因库中,并且还要满足没被访问过
if (hash2.count(t) && !hash1.count(t))
{
//在入队列的时候,先判断是否已经是最终结果了
if (t == endGene)
{
return ret;
}
//入队列
q.push(t);
//标记为已访问过
hash1.insert(t);
}
}
}
}
}
//没找到返回-1
return -1;
}
};
3.单词接龙
题目链接
题目:
样例输入和输出:
单词接龙这道题其实和最小基因变化是一样的,也是存在一个单词库,我们每次变化单词都需要考虑这个单词变化后的单词是否存在于单词库中,如果存在于单词库中这次变化才是合法的,如果没有这次不变化不合法,但是,这道题返回的和上道题是不一样的,这道题让我们返回变化过程中出现过的单词数目且是最少的,所以这道题在变化次数的基础上还要+1,因为第一个单词我们还没有算进去,这里算法原理我们就不讲了,和上道题一模一样。
代码展示:
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList)
{
unordered_set<string> hash1;
unordered_set<string> hash2(wordList.begin(), wordList.end());
int ret = 0;
queue<string> q;
q.push(beginWord);
hash1.insert(beginWord);
if (endWord == beginWord)return 1;
if (!hash2.count(endWord))return 0;
while (q.size())
{
ret++;
//求出队列大小
int sz = q.size();
//对每一层进行pop
while (sz--)
{
//取出队头元素
string tmp = q.front();
//pop队头元素
q.pop();
//对每一种情况进行遍历
for (int i = 0;i < beginWord.size();i++)
{
string t = tmp;
for (int j = 0;j < 26;j++)
{
t[i] = 'a' + j;
if (hash2.count(t) && !hash1.count(t))
{
if (t == endWord)
{
return ret + 1;
}
q.push(t);
hash1.insert(t);
}
}
}
}
}
return 0;
}
};
4.为高尔夫比赛砍树
题目链接
题目:
样例输入和输出:
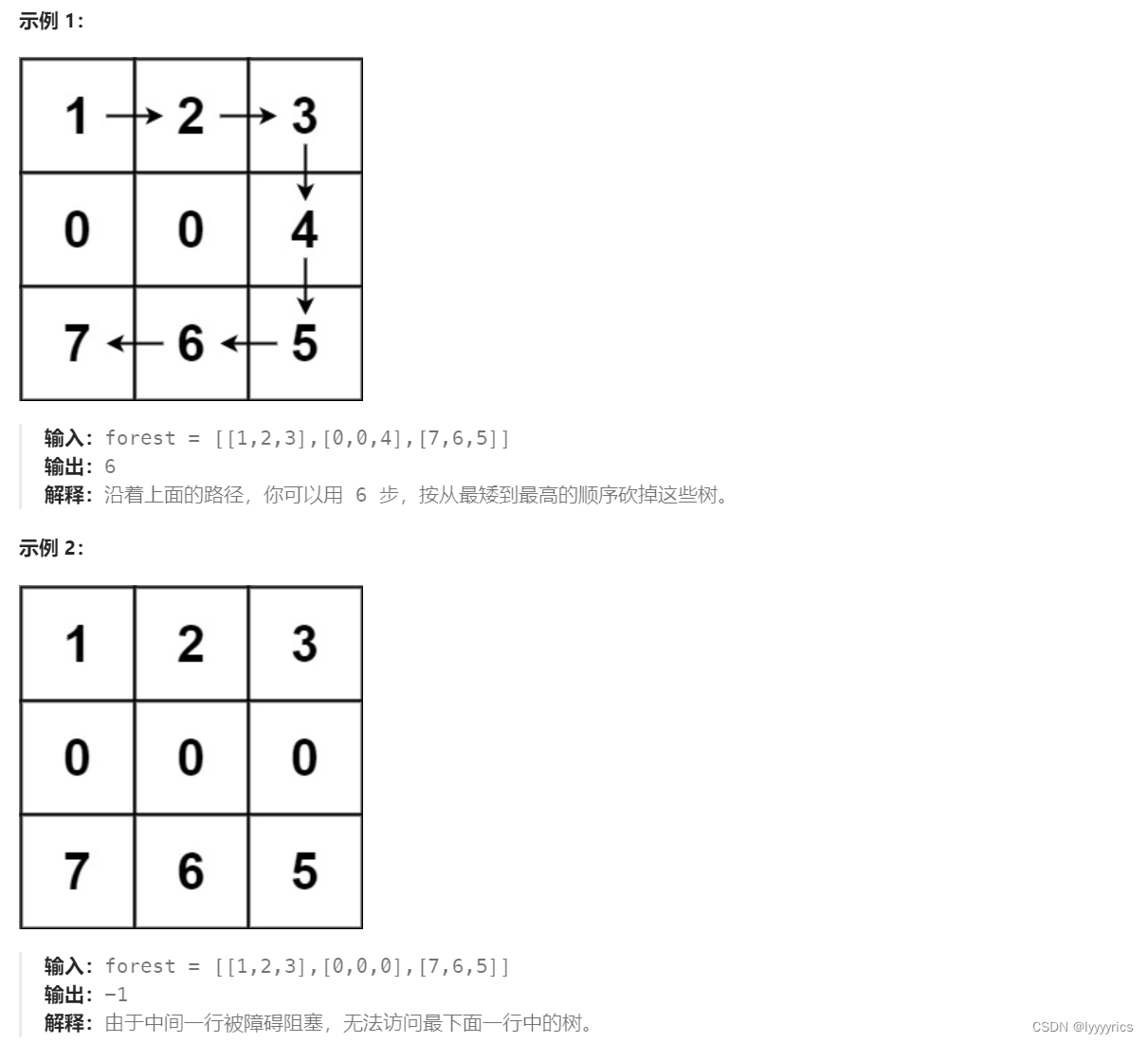
这道题就优点难度了,首先我们抓关键词,这道题0表示障碍,大于零的数表示可以走的路,大于1的表示树,这里树不是随便砍的,我们需要按照从大到小的顺序砍树,然后返回的是把所有树砍完需要的最小的步数,如果有树砍不到,则返回-1,大致就是这个意思,接下里我们用图画一下这道题。
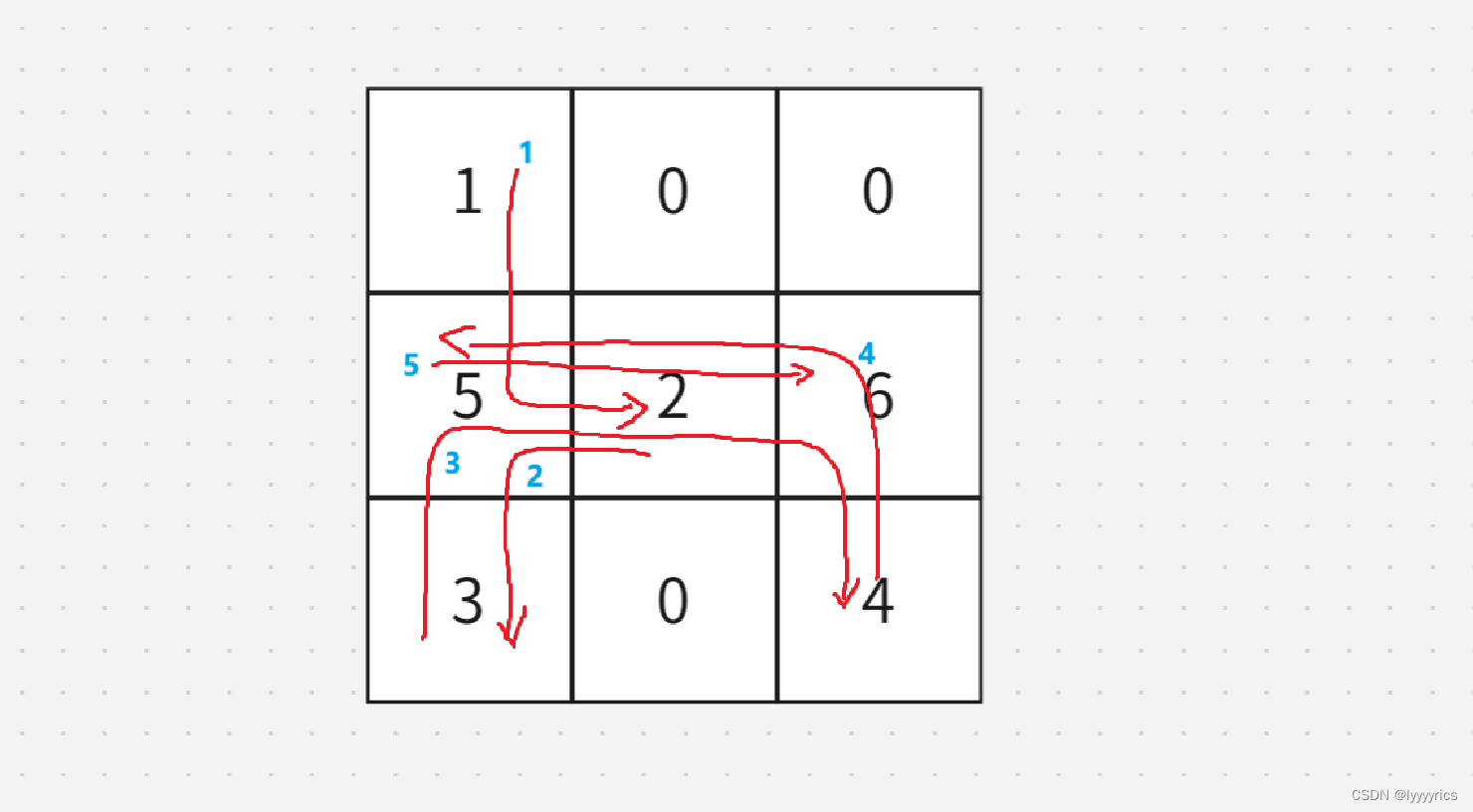
大致就是按照这个顺序开砍树的,按照1->2->3->4->5->6。这里我们其实可以看成n个最短路问题,
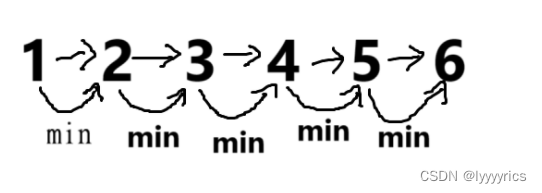
我们可以看做1到2的最短路加上2到3的最短路,加上3到4的最短路,再加上4到5的最短路,最后再加上5到6的最短路。看成n个最短路问题。
题目意思了解了,我们来讲讲算法原理:
算法原理:
我们转换为n个最短路问题之后,接下来问题就来了,我们该如何找到顺序呢,砍树的顺序,我们应该优先找到,我们用一个数组存需要砍树位置的小标,然后按照其对应的值进行排序,然后按照数组中排好序的顺序进行排序,每次砍完树的点就是下一次砍下一棵树的起始点然后对每次的起始点和终点做一次BFS找到最短路,这里的路注意是大于等于1的。
这道题我们也需要一个数组来表示每个节点的访问情况,但是需要注意的是,每次访问过后,我们都需要将上一次的访问记录给重置,保证每次都是一个新的访问记录的数组。
代码展示:
class Solution {
public:
typedef pair<int, int> PII;
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
bool vis[51][51];
int m, n;
int bfs(vector<vector<int>>& forest, int bx, int by, int ex, int ey)
{
//如果终点和起点重合则返回0步
if (bx == ex && by == ey)
{
return 0;
}
//定义一个队列
queue<PII> q;
//对vis进行重置,因为vis为全局变量,每次进入都会记录上次的数据,所以需要重置
memset(vis, 0, sizeof vis);
//将起点push进队列
q.push({ bx,by });
//标记对应下标的vis,表示已经访问过
vis[bx][by] = true;
//记录到终点的步数
int step = 0;
while (q.size())
{
//先把这层++
step++;
//求出这层的大小
int sz = q.size();
//循环pop
while (sz--)
{
//取队头的坐标
auto [a, b] = q.front();
//将队头pop
q.pop();
for (int i = 0;i < 4;i++)
{
int x = a + dx[i];
int y = b + dy[i];
if (x >= 0 && x < m && y >= 0 && y < n && forest[x][y] >= 1 && !vis[x][y])
{
if (x == ex && y == ey)
{
return step;
}
q.push({ x,y });
vis[x][y] = true;
}
}
}
}
return -1;
}
int cutOffTree(vector<vector<int>>& forest)
{
//求出森林的长和宽
m = forest.size(), n = forest[0].size();
//创建一个坐标索引数的数组
vector<PII> hash;
//将对应的有效的坐标存入数组中
for (int i = 0;i < m;i++)
for (int j = 0;j < n;j++)
if (forest[i][j] > 1) hash.push_back({ i,j });
//每次比较的时候拿出一个坐标,每次比较的方式是通过forest二维数组对应的坐标的值
sort(hash.begin(), hash.end(), [&](const pair<int, int>& p1, const pair<int, int>& p2)
{
return forest[p1.first][p1.second] < forest[p2.first][p2.second];
});
//按照顺序位置砍树
int bx = 0, by = 0;
int ret = 0;
//对坐标进行遍历
for (auto& [a, b] : hash)
{
//起始位置到终止为止的最短近距离
int step = bfs(forest, bx, by, a, b);
//如果step为-1证明有砍不到的树,则直接返回-1
if (step == -1)return -1;
//如果能砍掉这颗树则将step累加到ret上
ret += step;
bx = a, by = b;
}
//返回ret
return ret;
}
};
总结
通过这篇博客,我们深入探讨了广度优先搜索(BFS)在解决最短路径问题中的应用。从基础概念的介绍到具体算法的实现,我们一步步揭示了BFS的强大之处。BFS的核心在于其逐层搜索的策略,使其在无权图中能够高效地找到从起点到终点的最短路径。
BFS不仅适用于图论中的最短路径问题,还在很多实际场景中发挥着重要作用,例如社交网络分析、迷宫求解和网络爬虫等。通过具体的代码示例和图示,我们不仅展示了BFS的理论知识,也提供了实际应用中的操作指南。
希望通过本文,你不仅掌握了BFS解决最短路径问题的原理和方法,也能够在实践中灵活应用这一强大的算法工具。持续学习和探索,将使你在算法和数据结构的世界中走得更远。感谢你的阅读!