目录
一、*遍历二叉树
1.1遍历定义
1.2遍历目的
1.3遍历用途
1.4遍历方法
1.4.1先序遍历(DLR)
1.4.2中序遍历(LDR)
1.4.3后序遍历(LRD)
1.5根据遍历序列确定二叉树
1.6遍历算法的实现
1.6.1先序遍历算法的实现
1.6.2中序遍历算法的实现
1.6.3后序遍历算法的实现
1.6.4中序遍历的非递归算法
1.6.5二叉树的层次遍历
1.7二叉树遍历算法的应用
1.7.1按先序遍历建立二叉树的二叉链表
1.7.2复制二叉树
1.7.3计算二叉树深度
1.7.4计算二叉树结点总数
1.7.5计算二叉树叶子数
二、线索二叉树
2.1线索
2.2线索二叉树的存储结构
一、*遍历二叉树
1.1遍历定义
顺着某一条搜索路径巡防二叉树中的结点,使得每个结点均被访问一次,而且仅被访问一次(周游)
1.2遍历目的
得到树中所有结点的一个线性排列
1.3遍历用途
是树结构插入、删除、修改、查找和排序运算的前提
1.4遍历方法
依次遍历二叉树中的根结点、左子树和右子树,共有6种方案:
DLR、DRL、LDR、LRD、RDL、RLD
若规定先左后右,则DLR(先序遍历)、LDR(中序遍历)、LRD(后序遍历)
1.4.1先序遍历(DLR)
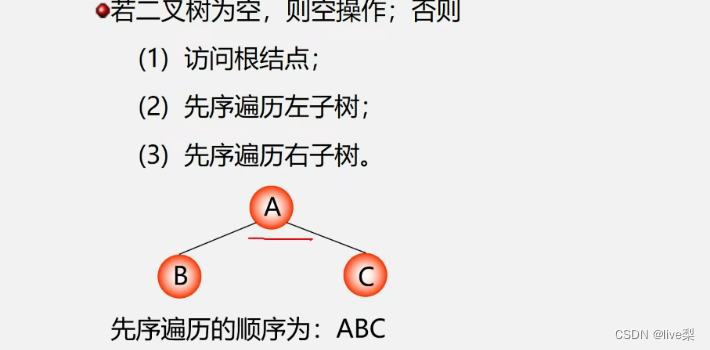
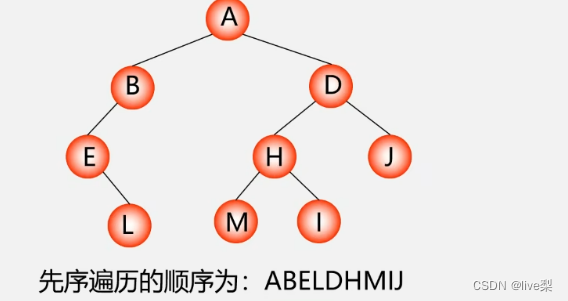
1.4.2中序遍历(LDR)
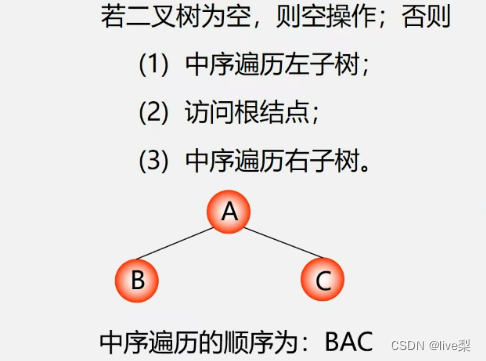
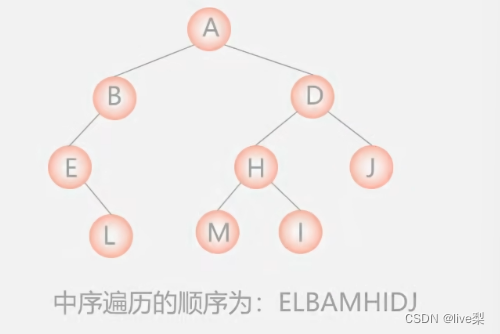
1.4.3后序遍历(LRD)
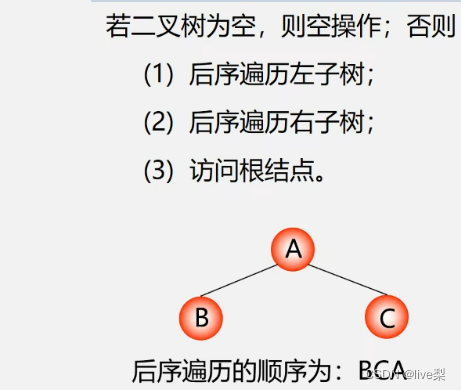
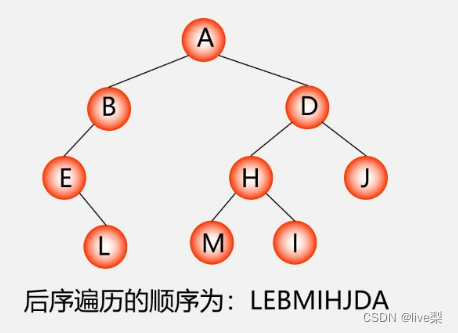
练习 ①
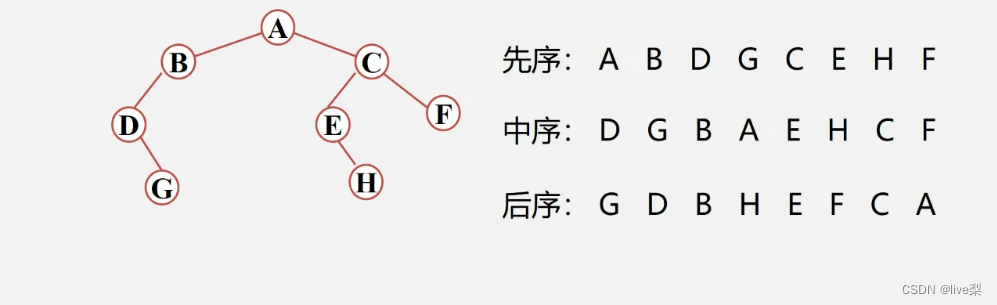
练习②

1.5根据遍历序列确定二叉树
由二叉树的先序序列和中序序列、后序序列和中序序列可以确定唯一一棵二叉树
①先序和中序例:
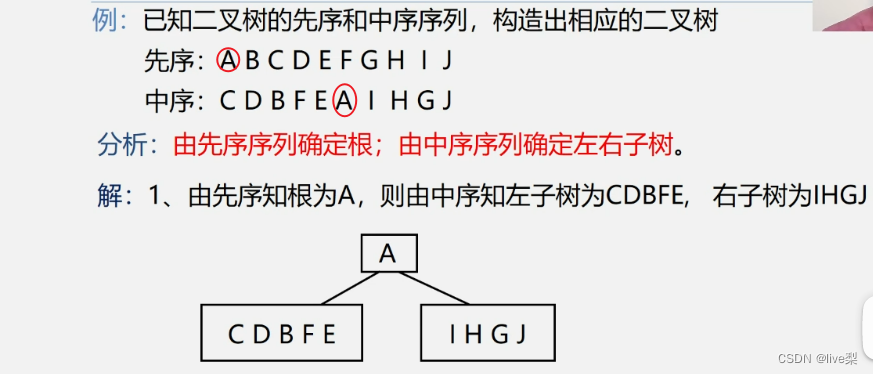
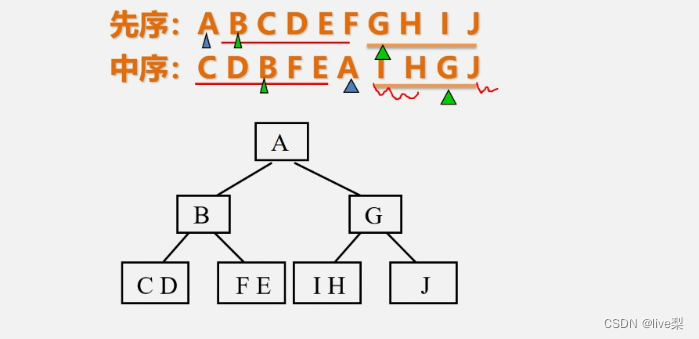
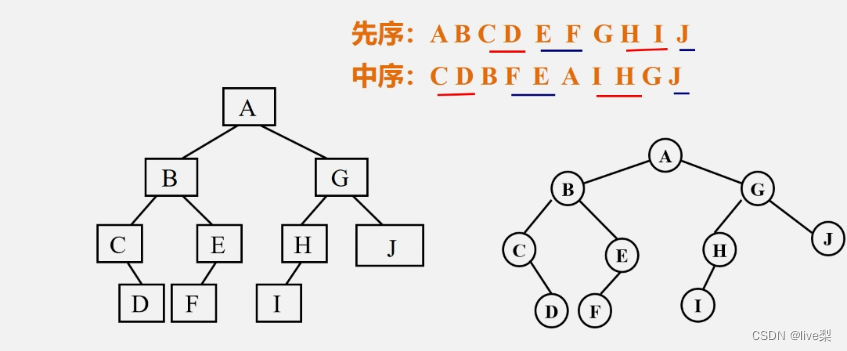 ②后序和中序例:
②后序和中序例:

1.6遍历算法的实现
1.6.1先序遍历算法的实现
Status PreOrderTraverse(BiTree T){
if(T==NULL) return OK; //空二叉树
else{
visit(T); //访问根结点
PreOrderTraverse(T->lchild); //递归遍历左子树
PreOrderTraverse(T->rchild); //递归遍历右子树
}
}
1.6.2中序遍历算法的实现
Status InOrderTraverse(BiTree T){
if(T==NULL) return OK; //空二叉树
else{
InOrderTraverse(T->lchild); //递归遍历左子树
visit(T); //访问根结点
InOrderTraverse(T->rchild); //递归遍历右子树
}
}1.6.3后序遍历算法的实现
Status PostOrderTraverse(BiTree T){
if(T==NULL) return OK; //空二叉树
else{
PostOrserTraverse(T->lchild); //递归遍历左子树
PostOrderTraversr(T->rchild); //递归遍历右子树
visit(T); //访问根结点
}
}时间和空间复杂度均为O(n)
1.6.4中序遍历的非递归算法
(用栈来实现:后进先出)
基本思想:①建立一个栈;②根结点进栈,遍历左子树;③根结点出栈,输出根结点,遍历右子树
Status InOrderTraverse(BiTree T){
BiTree p; InitStack(S); p=T;
while(p ||!StackEmpty(S)){
if(p) { Push(S,p); p=p->lchild;}
else { Pop(S,q); printf("%c",q->data);
p=q->rchild;}
};//while
return OK;
}
1.6.5二叉树的层次遍历
对于一棵二叉树,从根结点开始,按从上到下、从左到右的顺序访问每一个结点,每一个结点仅访问一次。
(用队列来实现)
基本思想:①将根结点进队;②队不空时循环:从队列中出列一个结点*p,访问它:若它有左孩子结点,将左孩子结点进队;若它有右孩子结点,将右孩子结点进队。
void LevelOrder(BTNode *b){
BTNode *p; SqQueue *qu;
InitQueue(qu); //初始化队列
enQueue(qu,b); //根结点指针进入队列
while(!QueueEmpty(qu)) { //队不为空,循环
deQueue(qu,p); //出队结点p
printf("%c",p->data); //访问结点p
if(p->lchild!=NULL) enQueue(qu,p->lchild); //有左孩子时将其进队
if(p->rchild!=NULL) enQueue(qu,p->rchild); //有右孩子时将其进队
}
}
1.7二叉树遍历算法的应用
1.7.1按先序遍历建立二叉树的二叉链表

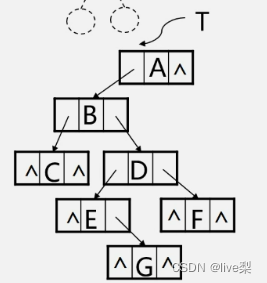
1.7.2复制二叉树

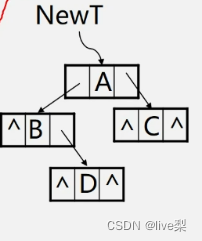
1.7.3计算二叉树深度


1.7.4计算二叉树结点总数
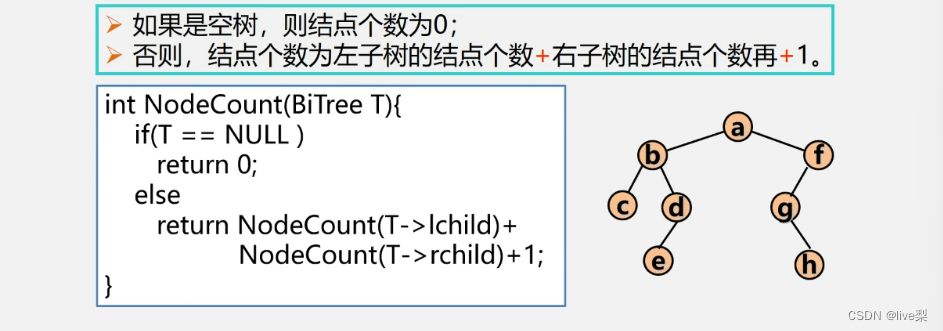
1.7.5计算二叉树叶子数

二、线索二叉树
2.1线索
改变指向的指针:若某个结点的左孩子为空,则将空的左孩子指针域改为指向其前驱;若某结点的右孩子为空,则将空的右孩子指针域改为指向其后继。

2.2线索二叉树的存储结构

Ltag=0 ——>lchild域指示结点的左孩子
Ltag=1 ——>lchild域指示结点的前驱
Rtag=0 ——>rchild域指示结点的右孩子
Rtag=1 ——>rchild域指示结点的后继
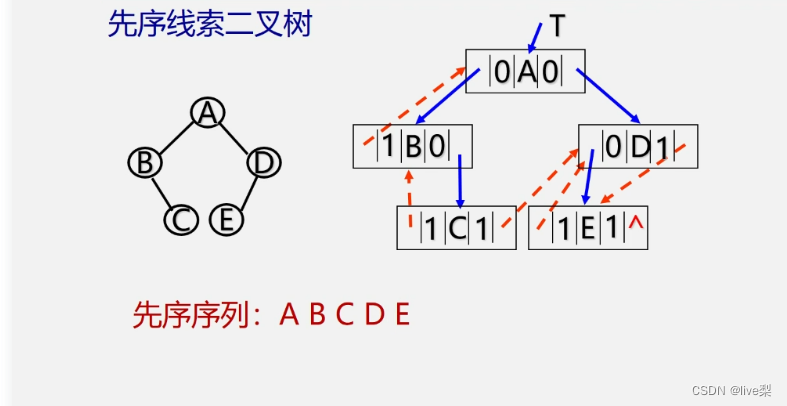
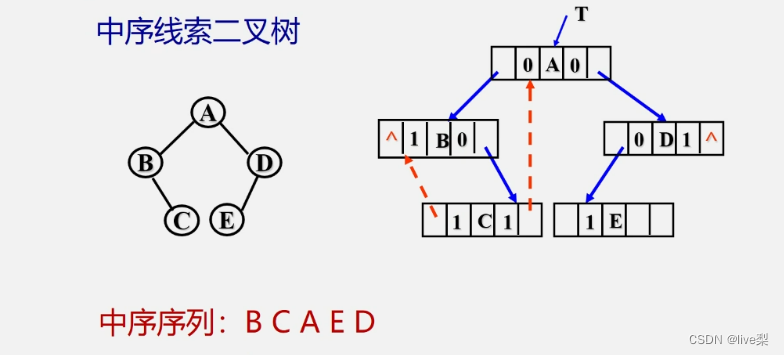
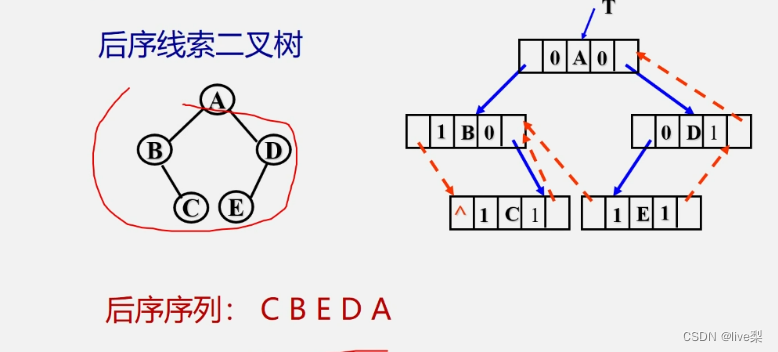
例
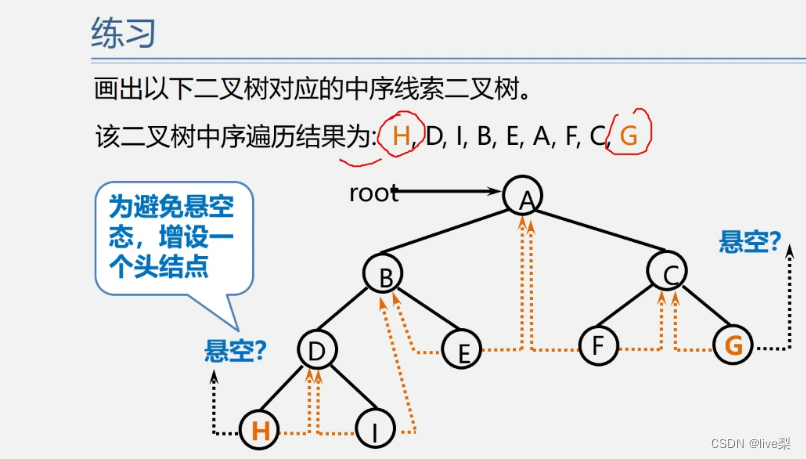
增设头结点