第四十七章 动态规划——状态压缩模型
- 一、什么是状态压缩
- 二、例题讲解
- 1、AcWing 1064. 小国王
- (1)问题
- (2)思路
- (3)代码
- 2、AcWing 327. 玉米田
- (1)问题
- (2)思路
- (3)代码
- 3、AcWing 292. 炮兵阵地
- (1)问题
- (2)思路
- (3)代码
- 4、其余比较难的题目
一、什么是状态压缩
根据我们第四十六章学习的状态机模型会发现某一事件会有多个状态,在某些题目中由于状态不同导致其转移方程也不同。那么这种情况下,我们需要用到状态机DP,即记录当前事件所处的状态,根据不同的状态去写方程。
而前一章节中所涉及的状态都是比较少的,所以我们可以凭借几个数字就能表示。但是当状态非常多并且抽象的时候,我们就需要用到今天所讲解的状态压缩。
比如给我们一行6个方格,现在在方格里填充0和1,我们把这一行看作一个事件,填充后的不同结果看作一个事件状态。那么总的事件状态就应该有26个。那么如果高效地表示这么多个状态呢?
我们现在将6个方格看成6位,0和1都看成二进制中的数字,那么这6位数字就会组成一个二进制数。比如000 010就是2。所以此时我们就实现了一个将抽象状态通过二进制压缩成1个十进制数字的过程,这个过程就叫做状态压缩。
二、例题讲解
以下例题作者在之前的文章中都做过详细地讲解,这里只做一些简单地介绍,详细的解答文章作者将附上链接。
1、AcWing 1064. 小国王
(1)问题
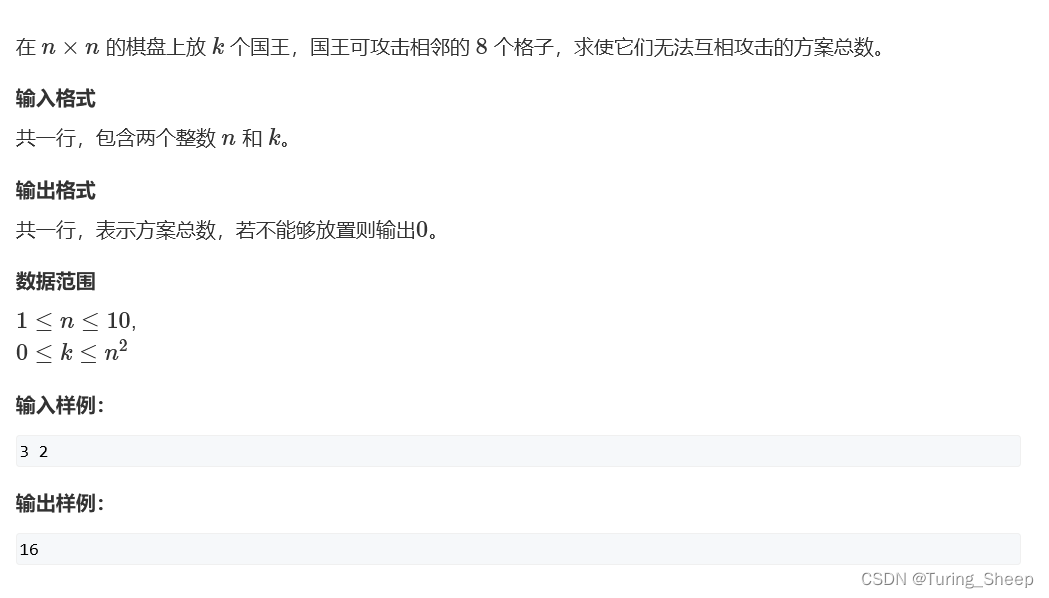
(2)思路
这道题的一个关键思路就是把每一行当作一个事件,然后由上一行推导出下一行的状态,由于每一行不同的状态就会导致下一行有不同的选择,所以我们需要记录一下行的状态,那么就需要将一行压缩为一个整数。
AcWing 1064. 小国王(状态压缩DP)
(3)代码
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=15,K=110,S=1<<10;
long long f[N][K][S];
int n,m;
vector<int>state;
vector<int>st[S];
bool check(int x)
{
for(int i=0;i+1<n;i++)
{
if((x>>i&1)&&(x>>(i+1)&1))return false;
}
return true;
}
int get_nums(int x)
{
int res=0;
for(int i=0;i<n;i++)
res+=x>>i&1;
return res;
}
int main()
{
cin>>n>>m;
for(int i=0;i<1<<n;i++)//记录所有对于本行而言合法的状态
if(check(i))state.push_back(i);
f[0][0][0]=1;
for(int i=1;i<=n+1;i++)//枚举i
{
for(int j=0;j<=m;j++)//枚举j
{
for(int ss=0;ss<state.size();ss++)//枚举第i-1行的状态
{
for(int s=0;s<state.size();s++)//枚举第i行的状态
{
if(!(state[ss]&state[s])&&(check(state[ss]|state[s])))//判断两行之间是否合法
{
int count=get_nums(state[s]);//计算第i行的国王数目
if(j>=count)
{
f[i][j][state[s]]+=f[i-1][j-count][state[ss]];
}
}
}
}
}
}
cout<<f[n+1][m][0]<<endl;
return 0;
}
2、AcWing 327. 玉米田
(1)问题
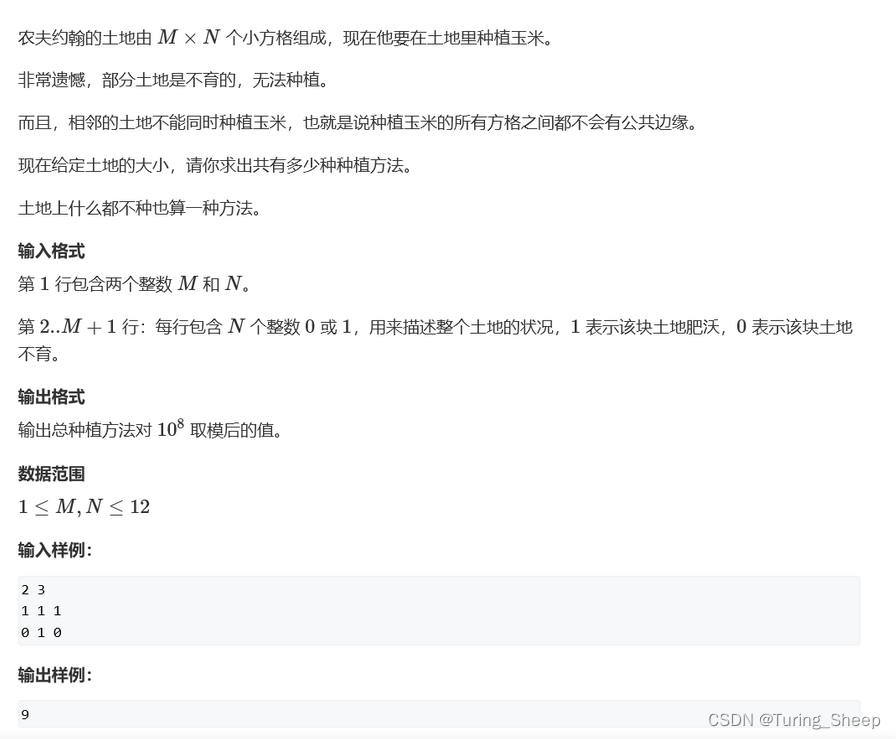
(2)思路
这道题和小国王那道题如出一辙,只是这道题对地图本身也做了一定的限制,所以我们就多了一个判断的条件。
AcWing 327. 玉米田(状态压缩DP)
(3)代码
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=15,S=1<<12,mod=1e8;
long long g[N],f[N][S];
vector<int>state;
int n,m;
bool check(int x)
{
for(int i=0;i+1<m;i++)
{
if((x>>i&1)&&(x>>(i+1)&1))return false;
}
return true;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=0;j<m;j++)
{
int x;
cin>>x;
g[i]+=(!x)*1<<j;
}
}
for(int i=0;i<1<<m;i++)
{
if(check(i))state.push_back(i);
}
f[0][0]=1;
for(int i=1;i<=n+1;i++)
{
for(int s=0;s<state.size();s++)
{
if(g[i]&state[s])continue;
for(int ss=0;ss<state.size();ss++)
{
if(g[i-1]&state[ss])continue;
if((state[s]&state[ss])==0)
f[i][state[s]]=(f[i][state[s]]+f[i-1][state[ss]])%mod;
}
}
}
cout<<f[n+1][0]<<endl;
return 0;
}
3、AcWing 292. 炮兵阵地
(1)问题

(2)思路
这道题和上面两道问题的区别在于,当前行的状态受前面两行的影响,所以我们需要多加一个维度。
AcWing 292. 炮兵阵地(状态压缩DP)
(3)代码
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int N=110,M=10,S=110;
int f[N][S][S];
int g[N];
vector<int>state;
int n,m;
bool check(int state)
{
for (int i = 0; i < m; i ++ )
if ((state >> i & 1) && ((state >> i + 1 & 1) || (state >> i + 2 & 1)))
return false;
return true;
}
int get_nums(int x)
{
int res=0;
for(int i=0;i<m;i++)
res+=(x>>i&1);
return res;
}
int main()
{
cin>>n>>m;
for(int i=2;i<=n+1;i++)
{
for(int j=0;j<m;j++)
{
char c;
cin>>c;
if(c=='H')g[i]+=1<<j;
}
}
for(int i=0;i<1<<m;i++)
if(check(i))state.push_back(i);
for(int i=2;i<=n+3;i++)
{
for(int j=0;j<state.size();j++)
{
if(state[j]&g[i-2])continue;
for(int s=0;s<state.size();s++)
{
if(state[s]&g[i-1])continue;
for(int ss=0;ss<state.size();ss++)
{
if(state[ss]&g[i])continue;
if( (state[j] & state[s]) || (state[j] & state[ss] ) || (state[s] & state[ss]) )
continue;
else
f[i][ss][s]=max(f[i-1][s][j]+get_nums(state[ss]),f[i][ss][s]);
}
}
}
}
cout<<f[n+3][0][0]<<endl;
return 0;
}
4、其余比较难的题目
状态压缩DP——蒙德里安的梦想
状态压缩DP——最短Hamilton路径
这两道题比较难,如果大家想进一步学的话,可以去读一读。