一、题目：

在这里插入图片描述

二、思路：

为了方便，我们利用下面这个图做讲解：
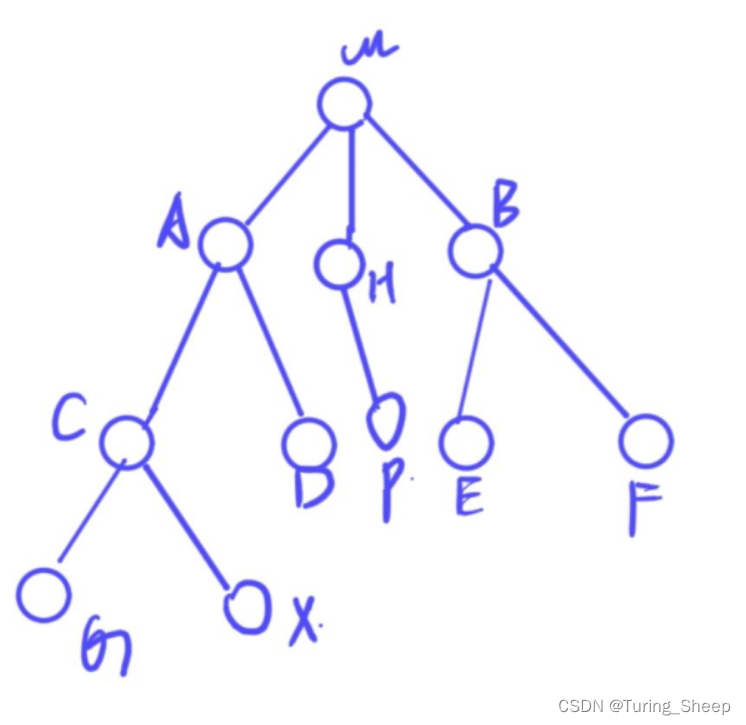
在这里插入图片描述
这颗树的最长路径必定经过的是图中的点，因此，**我们可以去枚举经过图中每个点的最长路径，然后再这些路径中选出一个最长的作为答案。**那么我们需要怎么做呢？

我们这里采用的是DFS（深度优先搜索），如果对DFS不了解的话，作者建议去看一下之前对DFS算法的专门讲解：第十三章 DFS与BFS（保姆级教学！！超级详细的图示！！）和第十四章图的存储及图的DFS（超级详细！！逐行解析！！）

很多同学不会写DFS，其实根本原因在于每道题中DFS递归函数的含义都是不一样的，而想要写出DFS就要明白DFS在每道题语境中的含义。

在本道题中，我们将DFS写成下面的样子：

int dfs(int u,int father)

**这个函数的作用是返回到u点最远的点的距离。**那么这么定义的作用是什么呢？

我们看下面的图：

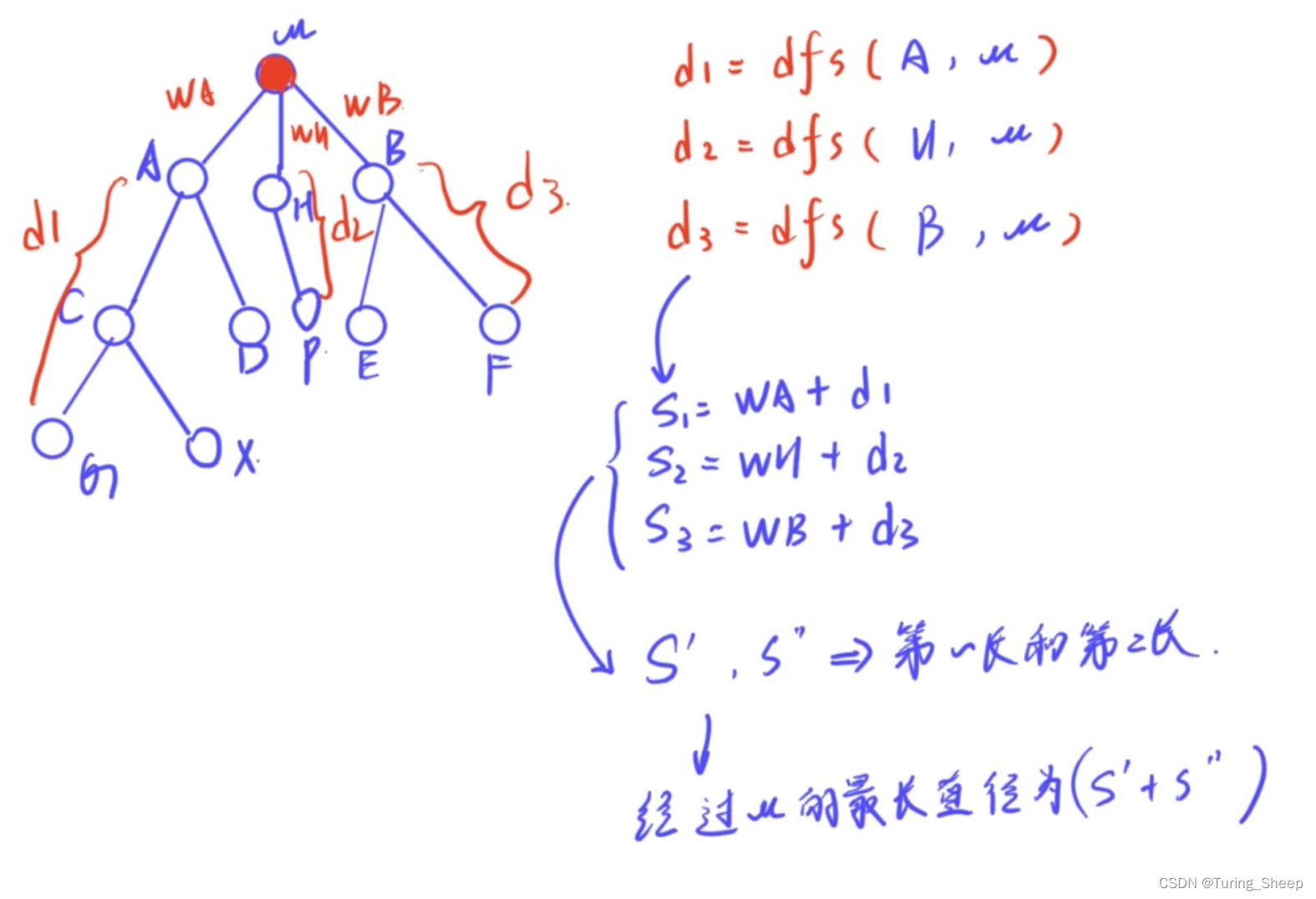
在这里插入图片描述
由于我们求的是最大距离，而最大距离必须要比较以后才能知道，因此就需要求出到u点的所有距离。然后我们选出前两个最大的。这样这两个距离和u点就构成了一个经过u点的最大路径。（详细过程如图中所示）

也就是说我们在求到u点的最大距离的过程中顺便求出了经过该点的最长路径。

并且，我们的DFS会去遍历每个点，所以经过每个点的最长路径都会求出来，此时我们只需要定义一个全局变量记录所有最长路径中最长的一个即可。

这里还有几个细节处理，前两个最大的距离组成了我们经过u点的最大距离，但是如果最大的距离中是负的，那么我们就不加上这个距离，因为加上的话只会减少。

另外，由于题目中是无向边，所以在遍历u的子节点的时候，也会遍历到u的父节点，所以我们参数中多写一个父节点，这样做的目的就是防止循环遍历造成死循环。

三、代码：

#include<bits/stdc++.h>
using namespace std;
typedef  pair<int,int> pii;
const int N=1e4+10;
vector<pii>g[N];
int n;
int ans;
int dfs(int u,int father)
{
    int d1=0,d2=0;
    for(int i=0;i<g[u].size();i++)
    {
        auto j=g[u][i];
        if(j.first==father)continue;
        int d=dfs(j.first,u)+j.second;
        if(d>=d1)
            d2=d1,d1=d;
        else if(d>d2)
            d2=d;
    }
    ans=max(ans,d1+d2);
    return d1;
}
int main()
{
    cin>>n;
    for(int i=0;i<n-1;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        g[a].push_back({b,c});
        g[b].push_back({a,c});
    }
    dfs(1,-1);
    cout<<ans<<endl;
    return 0;
}