Location: Beijing

1 大模型剪枝

Fig. 1.1大模型压缩-剪枝

剪枝的分类：结构化修剪对于简化大型语言模型和提高其效率尤其相关。非结构化修剪关注的是选择性地去除单个权重，旨在消除网络中不那么关键的连接。
修剪的基于阶段的分类：修剪可以在训练前、训练期间或训练后。

2 大模型持续学习

2.1 持续学习与基于持续学习的剪枝

持续学习侧重于在动态环境中适应大型语言模型，从而在不丢失先验知识的情况下实现持续学习。
在持续学习领域，剪枝的作用有助于有效地维护和进化神经网络结构，COPAL提出一种优化LLM的新方法，该方法绕过了再训练过程。

2.2 在LLM中持续修剪的缺点

持续修剪涉及到对不断进化的模型权重进行修剪，而不失去预训练的LLM的原始能力。

2.2.1 持续剪枝

持续剪枝在重点和方法上不同于基于持续学习的剪枝。基于持续学习的剪枝只是在不断进化的环境中使用剪枝来管理网络复杂性。相比之下，持续修剪是指在整个生命周期中发生的无训练修剪过程。面对所有遇到的数据集，持续剪枝会动态地调整相关的权重。

2.2.2 持续剪枝中的权重停滞(WS)

如果对已经归零的修剪权值保持不变，这导致在将模型从一个数据集转换到另一个数据集时没有响应。称这个概念为“权重停滞”（WS）。在下面是从校准引导的修剪策略中观察到的权重停滞的数学见解。
考虑到权值的重要性，以${\mathbf{W}}_i^{\ast }=|{\mathbf{W}}_i\cdot {\mathcal{R}}_i|$作为剪枝过程的基础，其中${\mathcal{R}}_i$是用一些标准对权值${\mathbf{W}}_i$进行缩放或排序。对于给定的数据集$i$、掩膜0器(原文叫mask)${\mathcal{M}}_i$和$\mathcal{I}$作为指标函数，得到的修剪权值矩阵${\mathbf{W}}_i^p$如下：
$$\begin{array}{rl}& {\mathcal{M}}_i=\mathcal{I}({\mathbf{W}}_i^{\ast }<{\mathcal{T}}_s)=\{\begin{array}{ll}0& \text{if }{\mathbf{w}}_i^{\ast }<{\mathcal{T}}_s,{\mathbf{w}}_i^{\ast }\in {\mathbf{W}}_i^{\ast }\\ 1& \text{otherwise.}\end{array},\\ & {\mathbf{W}}_i^p={\mathbf{W}}_i\cdot {\mathcal{M}}_i.\end{array}\text{\hspace{1em}(1)}$$
式中，阈值${\mathcal{T}}_s$根据目标的稀疏比$s$浮动，可以看出该公式的作用就是如果某个权值没有达到给定条件就置0，达到了就不变。
然而，对于下一个数据集$i+1$，需要剪枝的权重${\mathbf{W}}_{i+1}={\mathbf{W}}_i^p$，这个初始矩阵${\mathbf{W}}_{i+1}$已经有一组修剪（零）权重。最终这一次剪枝之后的权重矩阵如下：
$$\begin{array}{rl}& {\mathcal{M}}_{i+1}=\mathcal{I}\left({\mathbf{W}}_{i+1}^{\ast }<{\mathcal{T}}_s\right)\\ & \\ & =\mathcal{I}(|{\mathbf{W}}_i\cdot {\mathcal{R}}_{i+1}|\cdot |{\mathcal{M}}_i|<{\mathcal{T}}_s)={\mathcal{M}}_i,\\ & {\mathbf{W}}_{i+2}={\mathbf{W}}_{i+1}={\mathbf{W}}_i\cdot {\mathcal{M}}_i.\\ & \end{array}\text{\hspace{1em}(2)}$$
总结一下如下图

Fig. 1.2 WS

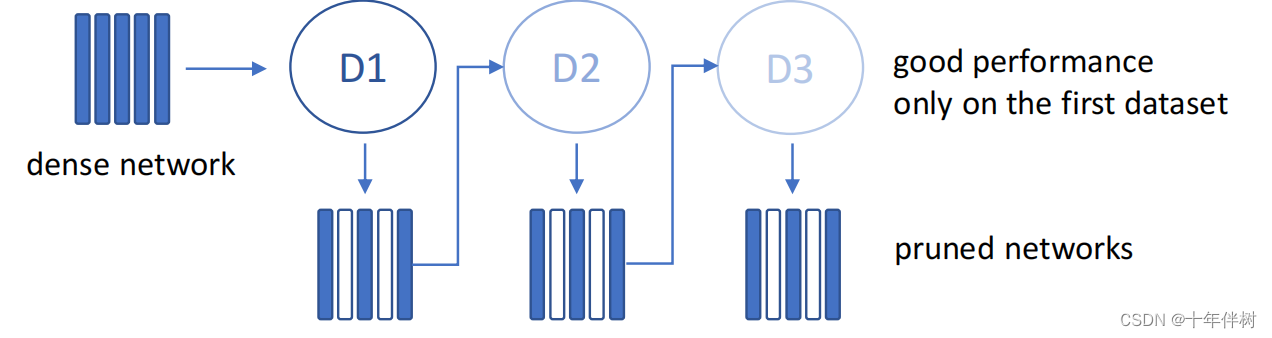
剪了个寂寞，这显然不合理。

2.2.3 持续剪枝中的遗忘问题（Forgetting）

当使用新的校准数据集更新修剪后的模型权值时，可以观察到这种健忘现象，这将降低以前遇到的数据集或任务的性能，如图1.3

Fig. 1.3 遗忘

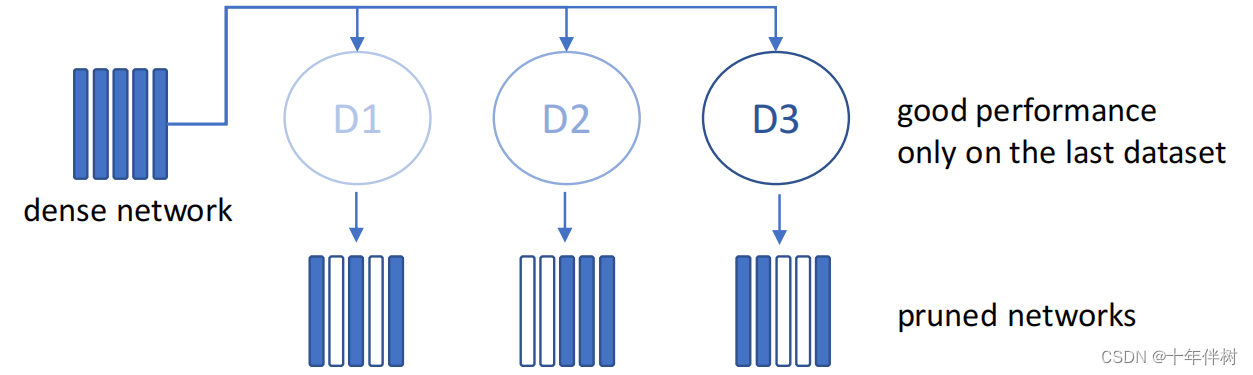
3 COPAL：基于敏感度分析的连续剪枝

这篇文章的主要创新点是寻找关键权重的方法。
为了克服遗忘和权重停滞，提出了一个基于敏感度分析的连续神经网络剪枝框架。总结这种方法如图3.1

Fig. 3.1 COPAL框架

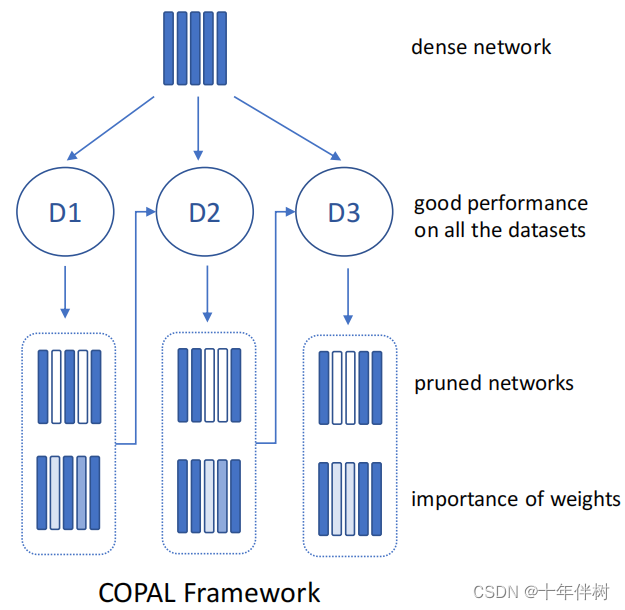
3.1 敏感度

对于神经网络的给定层，可以得出$\mathbf{y}$对$d{\mathbf{X}}_j^i$和$d\mathbf{W}$的敏感度，服从下式
$$d{\mathbf{y}}_j^i=\frac{\partial f}{\partial {\mathbf{X}}_j^i}d{\mathbf{X}}_j^i+\frac{\partial f}{\partial \mathbf{W}}d\mathbf{W}\text{\hspace{1em}(3)}$$
在实际应用中用$\Delta {\mathbf{X}}_j^i$和$\Delta \mathbf{W}$来代替$d{\mathbf{X}}_j^i$和$d\mathbf{W}$可以对$y$转化为灵敏度的表示如下式
$$\begin{array}{c}{S}_{\mathrm{W}}^{ij}=\frac{\partial f}{\partial \mathbf{W}}\times \Delta \mathbf{W},\\ S_{\mathbf{X}}^{ij}=\frac{\partial f}{\partial {\mathbf{X}}_i^i}\times \Delta {\mathbf{X}}_j^i.\end{array}\text{\hspace{1em}(4)}$$
$S_{\mathbf{W}}^{ij}$和$S_{\mathbf{X}}^{ij}$分别是对${\mathbf{y}}_j^i$对$\mathbf{W}$和$\mathbf{X}$的灵敏度量度，出于实际考虑，将公式4转化为下式
$$\begin{gathered} S_{\mathbf{W}}^{ij}=f(\mathbf{W}+\Delta \mathbf{W},{\mathbf{x}}_j^i)-{\mathbf{y}}_j^i, \\ {S}_{\mathbf{x}}^{ij}=f(\mathbf{W},{\mathbf{x}}_j^i+\Delta {\mathbf{x}}_j^i)-{\mathbf{y}}_j^i.\text{\hspace{1em}(5)} \end{gathered}$$
这些量分别反映了$\mathbf{W}$和$\mathbf{X}$对$y$的扰动，总结以上可得下式：
$$d{\mathbf{y}}_j^i=S_{\mathbf{W}}^{ij}+S_{\mathbf{x}}^{ij}\text{\hspace{1em}(6)}$$

3.2 关键权重的识别

将数据集$i$中第$j$个输入向量上的损失函数定义为$d{\mathbf{y}}_j^i$的欧几里得范数的平方如下式
$${\mathcal{L}}_j^i={\Vert d{\mathbf{y}}_j^i\Vert }_2^2.\text{\hspace{1em}(7)}$$
可以认为${\mathcal{L}}_j^i$越大，误差越大。将其与公式3联立得
$${\mathcal{L}}_j^i={\Vert \frac{\partial f}{\partial {\mathbf{x}}_j^i}d{\mathbf{x}}_j^i+\frac{\partial f}{\partial \mathbf{W}}d\mathbf{W}\Vert }_2^2.\text{\hspace{1em}(8)}$$
为了确定使$dy$最小的$\mathbf{W}$，使上式${\mathcal{L}}_j^i$计算对$d\mathbf{W}$的梯度，得
$${\nabla }_{d\mathbf{W}}{\mathcal{L}}_j^i=2d{\mathbf{y}}_j^i\frac{\partial f}{\partial \mathbf{W}}.\text{\hspace{1em}(9)}$$
（证明略）通过${\nabla }_{d\mathbf{W}}{\mathcal{L}}_j^i$，可以得出输出灵敏度$d{y}_j^i$的损失函数随权重灵敏度$d\mathbf{W}$变化的关系。
这里引入${\nabla }_{d\mathbf{W}}^{\prime }{\mathcal{L}}^k$来得到$k$个数据集的梯度的绝对值的和。这个量的绝对值大小对于理解损失函数对每个单独样本的敏感度很重要。通过关注这个量的大小，评估模型对$W$和$x$扰动的鲁棒性。${\mathcal{L}}^k$是数据集$k$的损失函数。
$$\begin{array}{rl}{\nabla }_{d\mathbf{W}}^{\prime }{\mathcal{L}}^k& =\sum _{i=0}^k\sum _j|{\nabla }_{d\mathbf{W}}{\mathcal{L}}_j^i|\\ & ={\nabla }_{d\mathbf{W}}^{\prime }{\tilde{\mathcal{L}}}^k+{\nabla }_{d\mathbf{W}}^{\prime }{\mathcal{L}}^{k-1}.\end{array}\text{\hspace{1em}(10)}$$
最后使用${\mathcal{L}}_j^i$沿$\mathbf{W}$的方向导数$\mathbf{D}$的大小来评估权重的重要性，方向导数$\mathbf{D}$的大小用${\mathbf{W}}_k^{\ast }$表示，公式表示为
$$\begin{array}{rl}{\mathbf{W}}_k^{\ast }& =\sum _{i=0:k}\sum _j\left|D_{\mathbf{W}}{\mathcal{L}}_j^i\right|=|\mathbf{W}|\cdot {\nabla }_{d\mathbf{W}}^{\prime }{\mathcal{L}}^k\\ & =\sum _j\left|\mathbf{W}\cdot {\nabla }_{d\mathbf{W}}{\mathcal{L}}_j^k\right|+{\mathbf{W}}_{k-1}^{\ast }\end{array}\text{\hspace{1em}(11)}$$
较高的${\mathbf{W}}_k^{\ast }$值表明损失函数对沿$\mathbf{W}$方向的权重的变化高度敏感，可以看出这些权重对模型的性能很重要。最终对$k$个数据集的梯度的绝对值的和较小的权重进行剔除，就得到了剪枝后的模型。
这篇文章解决遗忘问题的方式是对所有数据集都通用
COPAL¹
reference

---

1. COPAL: Continual Pruning in Large Language Generative Models ↩︎