图论中有时候会涉及到一些连通性问题,主要是针对于点来说,在有向图中有时候需要计算强连通分量,这时候代表分量的的点就非常重要;在无向图中有时候会需要知道割点,用到的算法都是Tarjan,这个算法还是有难理解(我是这么觉得)。
简单介绍
Tarjan主要基于深搜,其中有两个非常关键的标记数组,分别是dfn和low,同时引入概念时间戳tt,也就是到达这个点的时间,实际上就是搜索到的次序,dfn记录每个点的时间戳,即第一次访问到的号次,low也就是能到达的最早的时间戳,下面分析。
缩点
题目来源:【模板】缩点 - 洛谷
这一道题题意比较明显,就是你去走出一条路,点权之和最大,可以随便走,但是重复的点只算一次。
思考了就知道,如果有那么一个环(环就是1->2->3->1这样的)在,那么一定是要把环上面的点全部拿来的,因为你可以走一圈然后回到原来的地方,那么何乐而不为呢?于是我们可以把一个环的权值全部加到一点,然后重新建一张图,此时的图就是有向无环图,后面利用拓扑排序和dp,可以确定最大的权值。
如何缩点是这一题的重头戏,Tarjan算法基于深搜,每次会一股脑一直向下走,可以料想如果走到一个点发现走过了,那么再走上去是不是就成了一个环。
引入dfn数组存储时间戳,low存储这个点可以到达的点的最早时间戳,栈st存储点的情况,用于统计哪些点是在环上的,vis用于当前这一轮找点的情况。
得到一个点x,首先先入栈,然后将点的dfn和low均初始化为时间戳tt,然后开始查看与这个点相连的点,假设是to,如果这个点还没被访问过,也就是时间戳还是0,那么继续深搜,然后更新这个点的low值,也就是low[x]=min(low[x],low[to]);如果时间戳不是0,那么就看vis看是不是访问过,然后还是执行上面句子,为什么是这样呢,因为第一种是没有访问过,那么这个点的low值你是不知道的,所以无法更新,而访问过的可以直接得到值。在更新完所有与这个点连接的点之后就得到了这个点最终的low值。
在一轮更新之后,此时有着相同low值的就构成了一个强联通图,其中任意两点都可以互相达到。为什么?因为我们在更新时遇到访问过的点会停止搜索,那么遇到访问过的那么这个点的时间戳一定早于我走来到达这个点的这一条环(深搜是一条边走到黑)任意一点的时间戳,在回溯进行low[x]=min(low[to],low[x])的操作之后,这一条环上的所有low值都被置为了访问到的那个点的,一条环一定是强连通图,因为更新的过程中有许多交叉,其实都会被置为最小的那个,所以最终一个low相同的图可能由多个环组成,环组成的还是强连通图。
因为相同low值的是一个强连通图,而这个low值其实就是这个连通图最早被搜索到的值,我们就可以把这个点,也就是low[x]=dfn[x]的点作为这个强连通图的代表点,把这个连通图缩到这个点,至于如何找到这个代表点所代表的的块的所有节点就利用栈,一直弹到这个代表点出栈为止(因为这个点的low最小,所以最早进入栈)。
程序如下:
void tarjan(int x)
{
vis[x] = 1;
st.push(x);
low[x] = dfn[x] = ++tt; // 时间戳初始化
for (int i = last1[x]; i; i = e1[i].next)
{
int to = e1[i].to;
//双层次判断,dfn是全局标记,vis是当前轮标记
//dfn=0表示这个点还没有被纳入任何环,也没走过,这时候需要继续往下走,找完更新(回溯更新)
//vis!=0表示当前轮走过这个点然后又走到了,说明走出了一个环,那么直接更新,不用再找
if (!dfn[to]) //这个点还没有时间戳,走下去
{
tarjan(to);
low[x] = min(low[to], low[x]); //回溯的时候的更新
}
else if(vis[to])
low[x] = min(low[to], low[x]); //走到了一个点这一轮已经被访问过了,这就说明走出一个圈了
}
if (low[x] == dfn[x])//说明是关键点,关键点权重就是整个环的权重(把换上其他点权重加上来)
{
int tmp;
while (!st.empty())
{
tmp = st.top();
st.pop();
//printf("x=%d tmp=%d\n", x, tmp);
vis[tmp] = 0; //清除标记,因为是每一轮的标记(每次找环要清除标记)
squ[tmp] = x;
if (x == tmp)break;//表示到了环的根节点
p[x] += p[tmp]; //缩点
}
}
}这个过程比较抽象,举个例子,简单起见如下图所示:
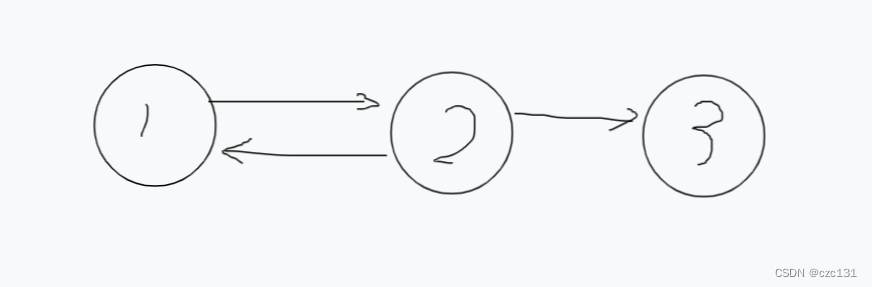
从1进入程序:
1入栈,dfn[1]=low[1]=1,1->2,因为dfn[2]=0,可以搜索2;
2入栈,dfn[2]=low[2]=2,2->1,3,先去1,发现dfn[1]!=0,已经搜过,那么直接更新low[2]=min(low[2],low[1])=1
再看3,因为dfn[3]=0,可以搜索3;
3入栈,dfn[3]=low[3]=3,3->无,不能继续搜索;
判断发现dfn[3]=low[3],所以可以作为一个强连通图,开始从栈弹出点,弹出3,3=3结束,找到第一个分量3;
回溯,回到2,更新low[2]=min(low[2],low[3])=1,不变,不能继续搜索;
判断发现dfn[2]=2,low[2]=1,不相等;
回溯,回到1,
发现dfn[1]=low[1]=1,可以作为一个强连通图,开始从栈弹出点,弹出2,1,1=1结束,找到第二个连通分量1,2。、
在弹栈的时候可以把权重都加到代表点上,就可以完成缩点操作。
接下去因为要计算权值最大,我们在缩点之后重新建图,就可以得到一张新的无环有向图,利用dis[x]=min(dis[x],dis[to]+p[x])加上拓扑排序就可以计算出答案。
完整代码:
#include<stdio.h>
#include<algorithm>
#include<stack>
#include<queue>
#define Inf 0x3f3f3f3f
#define N 11000
#define M 110000
using namespace std;
int n, m, p[N];
bool vis[N];
int low[N], dfn[N],tt;//最小时间戳,当前时间戳,时间戳
int squ[N];//存储每个点所属的连通块的关键点
int du[N];//存储每个点的入度
int dis[N];//存储每个点的大小
stack<int>st;//存储暂时的答案序列(一个环的)
queue<int>q;//topo排序会用到
struct Edge
{
int next, from, to;
}e1[M*5],e2[M*5];
int last1[N], last2[N], cnt1,cnt2;
void add(int from, int to, Edge e[],int last[],int &cnt)
{
e[++cnt].to = to;
e[cnt].from = from;
e[cnt].next = last[from];
last[from] = cnt;
}
//tarjan算法本质就是找出一个个圈,因为只要一走到走过的点就形成一个环,此时是强连通图,可以缩成一个点
void tarjan(int x)
{
vis[x] = 1;
st.push(x);
low[x] = dfn[x] = ++tt; // 时间戳初始化
for (int i = last1[x]; i; i = e1[i].next)
{
int to = e1[i].to;
//printf("x=%d to=%d last[x]=%d\n", x, to,last1[x]);
//双层次判断,dfn是全局标记,vis是当前轮标记
//dfn=0表示这个点还没有被纳入任何环,也没走过,这时候需要继续往下走,找完更新(回溯更新)
//vis!=0表示当前轮走过这个点然后又走到了,说明走出了一个环,那么直接更新,不用再找
if (!dfn[to]) //这个点还没有时间戳,走下去
{
tarjan(to);
low[x] = min(low[to], low[x]); //回溯的时候的更新
}
else if(vis[to])
low[x] = min(low[to], low[x]); //走到了一个点这一轮已经被访问过了,这就说明走出一个圈了
}
if (low[x] == dfn[x])//说明是关键点,关键点权重就是整个环的权重(把换上其他点权重加上来)
{
int tmp;
while (!st.empty())
{
tmp = st.top();
st.pop();
//printf("x=%d tmp=%d\n", x, tmp);
vis[tmp] = 0; //清除标记,因为是每一轮的标记(每次找环要清除标记)
squ[tmp] = x;
if (x == tmp)break;//表示到了环的根节点
p[x] += p[tmp]; //缩点
}
}
}
//topo排序+dp
int topo()
{
for (int i = 1; i <= n; i++)
if (squ[i] == i && du[i] == 0) //关键点入队
{
q.push(i);
dis[i] = p[i];
}
while (!q.empty())
{
int x = q.front();
q.pop();
for (int i = last2[x]; i; i = e2[i].next)
{
int to = e2[i].to;
du[to]--;
dis[to] = max(dis[to], dis[x] + p[to]);
if (du[to] == 0)q.push(to); //度为0入队
}
}
int ans = 0;
for (int i = 1; i <= n; i++)
ans = max(ans, dis[i]);
return ans;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", p + i);
int x, y;
for (int i = 1; i <= m; i++)
{
scanf("%d%d", &x, &y);
add(x, y, e1, last1, cnt1); // 全局变量传进去也只是形参
}
for (int i = 1; i <= n; i++)
if (!dfn[i]) //没有时间戳代表是没访问过
tarjan(i);
for (int i = 1; i <= m; i++)
{
int x = squ[e1[i].from];
int y = squ[e1[i].to];
if (x != y) // 去除自环
{
add(x, y, e2, last2, cnt2);
du[y]++;
}
}
int ans = topo();
printf("%d\n", ans);
return 0;
}割点
题目来源:【模板】割点(割顶) - 洛谷
割点就是在无向图中,一个点去掉了,图就不再连通了,那么这个点就是割点。
那么如何寻找割点,实际上也是利用tarjan算法, 各种定义类似于上题,不过因为在无向图中,任意连通块总是强连通图,这就使得上题定义的low失去了意义,因为只要连通,那么最终所有节点的low值均相等,所以在这里的low的更新方式稍稍改变,也就是程序中的low[x] = min(low[x], dfn[to])。
割点有两种情况,假设有下面这么一张图:
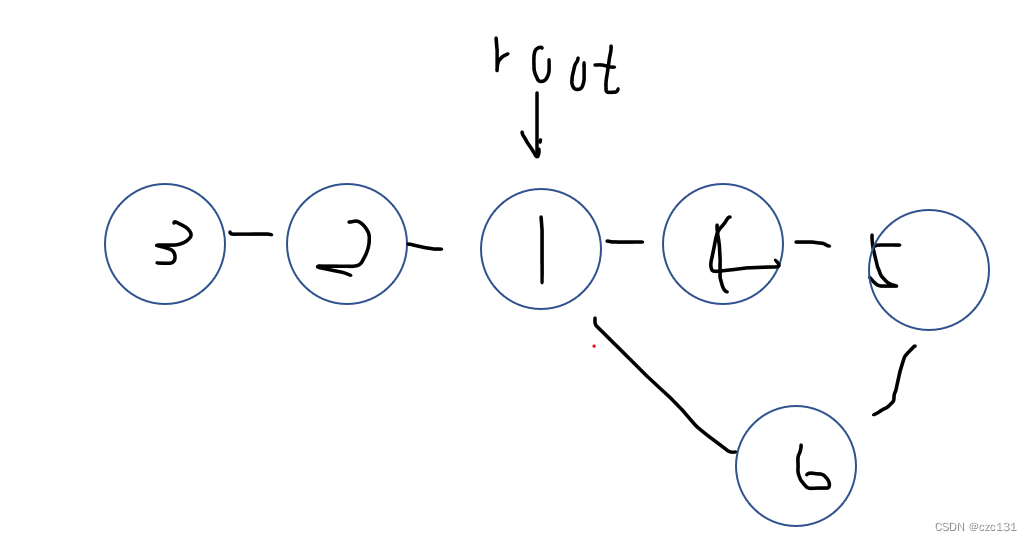
第一种是对于根节点(最开始的点,一个连通块仅一个,随便设置),因为深搜每次会搜索完一块与根节点相连的,要是根节点连接了两块或更多,那么这个根节点就是割点。假设1是根节点,那么第一次搜索完2、3,第二次搜索完4、5,有两块,所以1是割点。
第二种情况是像2不是根节点的,这种就需要判断与他相连的点能不能不通过这个点到达更早的点,比如3只能通过2到达1,而5除了通过4,还可以通过6。
设定根节点root,x点进入,先初始化low和dfn为时间戳,开始检查所有相连点to,如果dfn!=0也就是已经访问过,那么直接更新low[x] = min(low[x], dfn[to]),为什么是dfn[to]而不是low[to],首先无向图都是双向边,要是low[to]那么全都是一样了,这样更新之后low存储了所有直接相连边中的时间戳最小值,也是为了下面的判断;如果dfn=0也就是没访问过,那么继续搜索,计算出low[to]后更新low[x]=min(low[x],low[to]),要是low[to]>=dfn[x]的话,就说明下一个点找遍也无法找出比x更早出现的点,所以x为割点。
部分代码:
void tarjan(int x,int root)
{
//printf("x=%d\n", x);
int child = 0;
low[x] = dfn[x] = ++tt;
for (int i = last[x]; i; i = e[i].next)
{
int to = e[i].to;
if (!dfn[to]) //这个点还没有被找过,那么继续找,可能会找到更早的
{
tarjan(to, root);
low[x] = min(low[to], low[x]);//更新当前值,如果能找到更早的,传给x
//printf("low[%d]=%d dfn[%d]=%d\n", to,low[to],x,dfn[x]);
if (low[to] >= dfn[x] && x != root)
//相当于说把下一个点to找遍了相连的,找不到一个直接与to相连的点比x更早出现
flag[x] = 1;
if (x == root)child++;//child就是一个个块
//根节点遍历一次找一个块,这个块与其他与根节点相连的块只能通过根节点相连(因为一旦dfn!=0就不tarjan了)
/* example:
2 1 3 5 6
4
*/
//假设3是根节点,3第一次找把21找了,child=1,第二次找了56,child=2,,第三次找了4,child=3>2,所以3是割点
}
low[x] = min(low[x], dfn[to]);
//这个地方一定要注意!如果把dfn写做low的话那么一个连通块的low实际上都是根节点low值
//low[x]始终存储与x相连的最早出现的时间戳
}
if (x == root && child >= 2)
flag[root] = 1;
}
结合判断条件low[to]>=dfn[x],还有搜索后的low[x]=min(low[x],low[to])再来理解一下为什么是dfn[to]。
首先因为每次遇到一个相连的点,如果to 没有访问过,那么就会对to进行深搜,由于low[x]=min(low[x],low[to])的存在,那么如果to能够通过其他路径到达了比x更早的位置,那么就可以继承其low值从而使得low[to]<dfn[x]。比如x=4,to=5,5可以通过6继承到1的low值,这个值比4的dfn要小,所以low[5]<dfn[4],4不是割点。
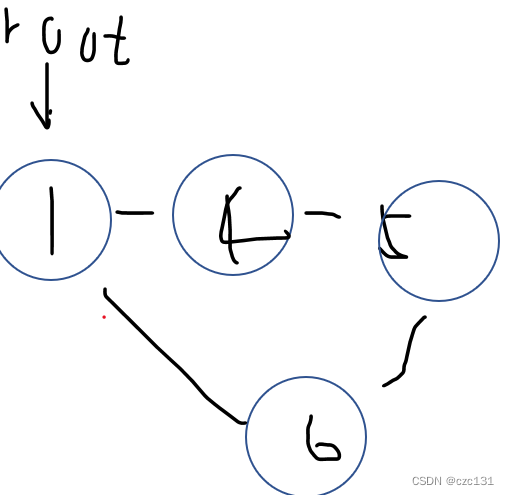
要是没有其他路可以走到更早的位置,那么最终low[to]>=dfn[x],那么这个点就是割点。比如
2->3,3没有路可以走到2的前面,所以low[3]=dfn[2],2作为割点。
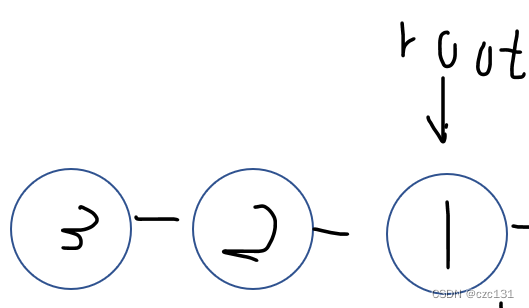
其余细节不再赘述。
完整代码:
#include<stdio.h>
#include<algorithm>
using namespace std;
#define Inf 0x3f3f3f
#define M 500000
#define N 50000
bool flag[N];//存储点是否为割点
int num; //存储割点个数
int n, m;
int dfn[N], low[N], tt;
//low存储可以连到的最早出现的时间戳
struct Edge
{
int to, next;
}e[M*5];
int last[N], cnt;
void tarjan(int x,int root)
{
//printf("x=%d\n", x);
int child = 0;
low[x] = dfn[x] = ++tt;
for (int i = last[x]; i; i = e[i].next)
{
int to = e[i].to;
if (!dfn[to]) //这个点还没有被找过,那么继续找,可能会找到更早的
{
tarjan(to, root);
low[x] = min(low[to], low[x]);//更新当前值,如果能找到更早的,传给x
//printf("low[%d]=%d dfn[%d]=%d\n", to,low[to],x,dfn[x]);
if (low[to] >= dfn[x] && x != root)
//相当于说把下一个点to找遍了相连的,找不到一个直接与to相连的点比x更早出现
flag[x] = 1;
if (x == root)child++;//child就是一个个块
//根节点遍历一次找一个块,这个块与其他与根节点相连的块只能通过根节点相连(因为一旦dfn!=0就不tarjan了)
/* example:
2 1 3 5 6
4
*/
//假设3是根节点,3第一次找把21找了,child=1,第二次找了56,child=2,,第三次找了4,child=3>2,所以3是割点
}
low[x] = min(low[x], dfn[to]);
//这个地方一定要注意!如果把dfn写做low的话那么一个连通块的low实际上都是根节点low值
//low[x]始终存储与x相连的最早出现的时间戳
}
if (x == root && child >= 2)
flag[root] = 1;
}
void add(int from, int to)
{
e[++cnt].to = to;
e[cnt].next = last[from];
last[from] = cnt;
}
int main()
{
scanf("%d%d", &n, &m);
int x, y;
for (int i = 1; i <= m; i++)
{
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);//无向图双向建边
}
for (int i = 1; i <= n; i++)
if (!dfn[i])
tarjan(i,i);//把i作为根节点,寻找割点
for (int i = 1; i <= n; i++)
printf("i=%d low=%d dfn=%d\n", i, low[i], dfn[i]);
for (int i = 1; i <= n; i++)
if (flag[i])
num++;
printf("%d\n", num);
for (int i = 1; i <= n; i++)
if (flag[i])
printf("%d ", i);
printf("\n");
return 0;
}感觉脑子已经一片空白了,就这样吧
![用Devc++与easyx一步一步做游戏[启动界面部分]-之按钮制作](https://img-blog.csdnimg.cn/f59b1119fc6d4d5a9011efe6f30000d3.png)