​

1. 题目描述

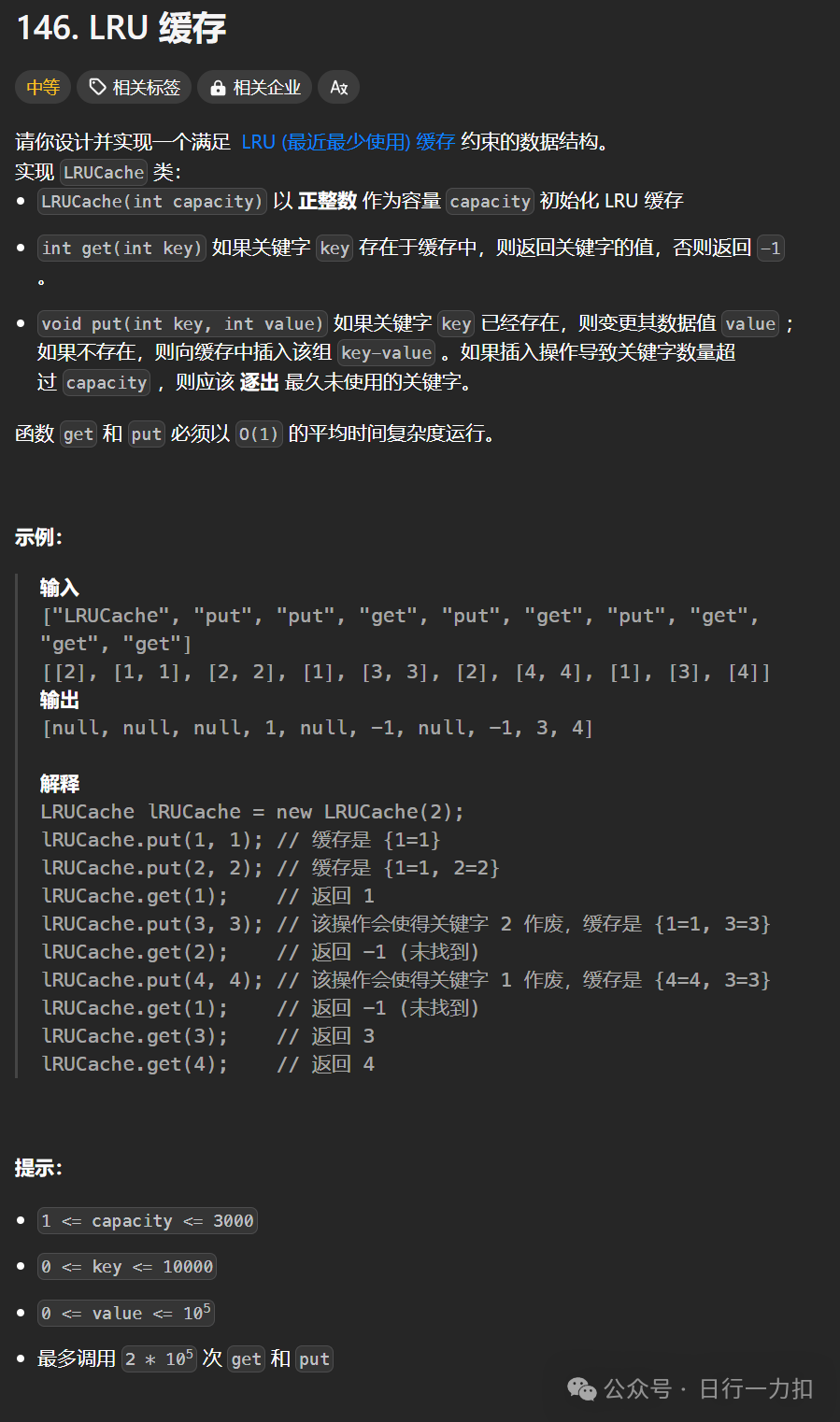
2.  题目分析与解析

首先讲解一下LRU

LRU 是“Least Recently Used”的缩写，LRU 算法的基本思想是跟踪最近最少使用的数据，并在缓存已满且需要存储新数据时优先驱逐该数据。

LRU 算法通常的工作原理的简化解释：

1. 当访问或使用一条数据时，将该数据移动到“最近使用”的列表的前面。

2. 当缓存已满且需要存储新数据时，算法会查看列表的末尾，以找到最近最少使用的数据。

3. 然后，最近最少使用的数据将被从缓存中驱逐，以腾出空间存储新数据。

这个过程确保了最近使用的数据保留在缓存中，而较旧、使用频率较低的数据在需要时被驱逐。这有助于通过最大限度地确保最相关的数据随时可用来提高缓存系统的效率。

2.1 思路一

注意题目中提示的 函数 get 和 put 必须以 O(1) 的平均时间复杂度运行 ，根据这个信息可能在提示我们是不是会用hashMap（因为O(1)）。但是如果使用hashMap我们怎么跟踪它最近是否被使用呢？这时我们可能也会想到使用一个队列，按照队列先进先出的性质，我们就可以实现在容量不够时移除最近最少使用的那个对象。但是如果使用队列也会面临一个问题，那就是如下图所示的情况：

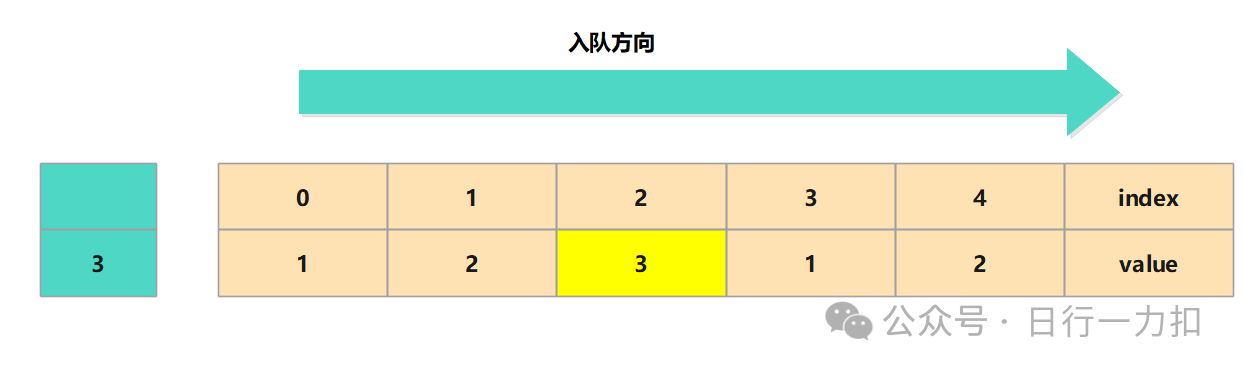
这时如果我要put进去的value为3，那我就需要把队列更新为如下形式：

那就牵涉到了队列的重新更新，肯定无法实现O(1)的要求。

而此时我们想象一下如果对于一个新用到的元素，那必然要把它更新到这个LRU的链子的头部就像上图 3 放在0号位一样，能够在常数时间内进行这样移动的好像链表就能行。

现在我们假设使用链表，对于前面同样的情况：

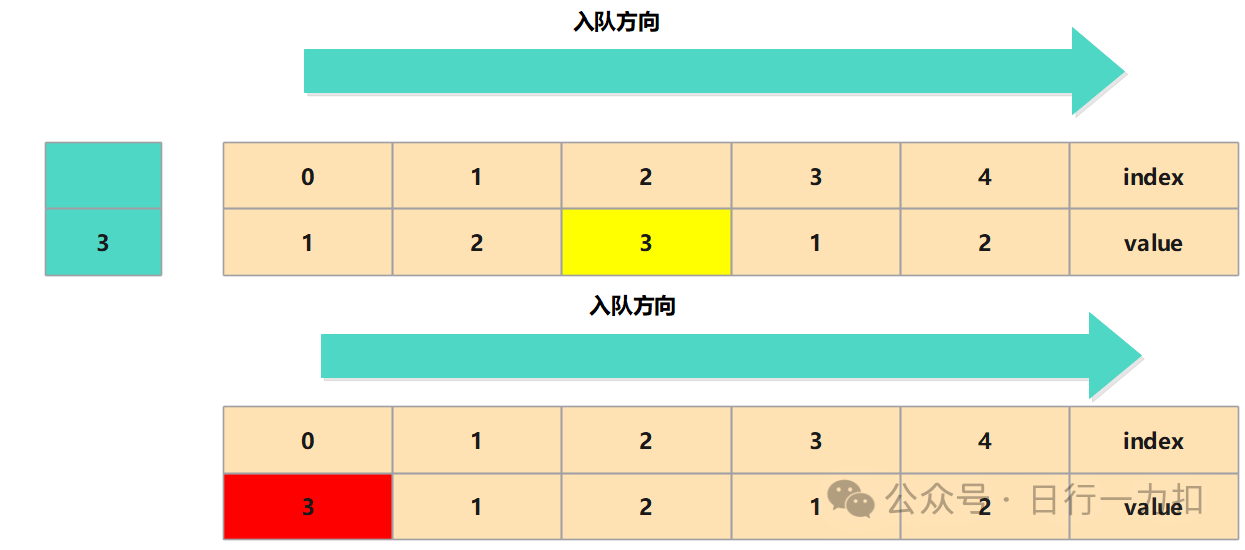
换成链表后就是一个个单独的节点，那么移动只需要找到当前需要put的节点，找到它的位置及其前后节点，将当前节点放在链表头部，前后节点进行连接不就可以完成题目的要求。注意一下要想在O(1)的时间复杂度中找到这个节点，还是要借助hash。因此我们就可以提出以下思路：

解题思路：

整体思路——构建环形链表，每次插入新节点时，将尾部节点删除（也就是替换），将新节点插入到头部（也是替换）

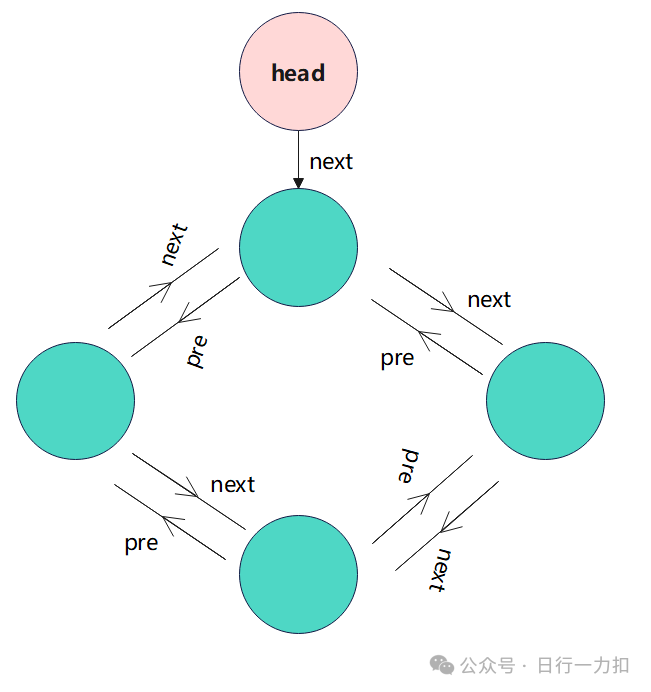
1. 定义一个HashMap存储key和Node

2. 定义一个虚拟头节点指向环形链表的头部

3. 构造函数：构建一个capacity长度的双向环形链表

4. get方法：如果key不存在，返回-1；如果key存在，返回value，并将当前节点移动到头部

5. put方法：如果key存在，更新value，并将当前节点移动到头部；如果key不存在，将新节点插入到头部并将尾部节点删除

6. 移动到头部方法：如果当前节点是头部节点，直接返回；如果当前节点是中间节点，将当前节点的前一个节点和后一个节点连接，将当前节点插入到头部

7. 时间复杂度：get和put方法的时间复杂度都是O(1)

8. 空间复杂度：O(n)

3. 代码实现

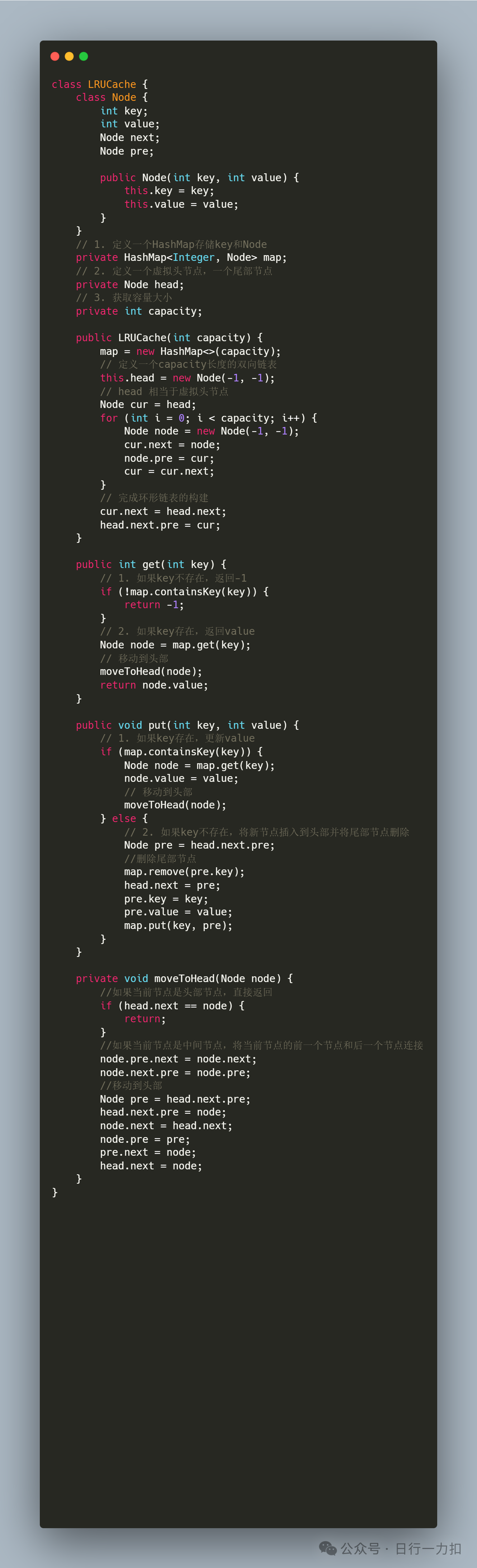
4. 相关复杂度分析

这个LRUCache实现的时间复杂度主要集中在put和get方法上。

时间复杂度分析：

1. get(int key):

   • 在HashMap中查找key的时间复杂度是O(1)。

   • 如果key存在，调用moveToHead方法，该方法的时间复杂度是O(1)。

   • 因此，get方法的总体时间复杂度是O(1)。

2. put(int key, int value):

   • 如果key已经存在，需要更新其对应的value，这涉及到HashMap的查找和更新操作，时间复杂度均为O(1)。

   • 如果key不存在，需要将新节点插入到头部并将尾部节点删除，这包括HashMap的插入和删除操作，以及moveToHead方法的调用，总体时间复杂度也是O(1)。

   • 因此，put方法的总体时间复杂度是O(1)。

空间复杂度分析：

LRUCache类中使用了HashMap来存储键和节点的映射关系，其空间复杂度为O(capacity)。另外，还有capacity个节点，每个节点占用的空间也是常数级的。因此，LRUCache的总体空间复杂度为O(capacity)。

综上所述，该LRUCache实现的时间复杂度为O(1)，空间复杂度为O(capacity)。