来源：河北工业职业技术大学 安彤彤 彭金杉 张家硕

题目

薪资发放问题

一般公司给职员发放薪金，通常按每月等额发放。某公司即将改进薪金发放方案，允许任职5年以上的职员向公司财务部门申请工资每月可变额度发放，每月工资发放额度不超过年收入20%，前半年收入不超过年收入的80%, 剩余部分则作为年终奖在年底一次性发放。 职员们想通过调整每月的预发金额以及年终一次性发放金额，使得一年内个人的总收益最高。

针对以下各种情况。

1. 请你查阅国家个人所得税税率表，为薪金年收入分别为8万元、12万元、18万元的职员们设计个人薪金领取方案，合理避税，使得一年的税后收入最高。
2. 该公司部分职员每月可以将80%收入用于一些投资理财项目，如某些收益宝（百赚、余额宝等）、开放式基金、银行存款、债券、股票等, 请为他们设计个人薪金领取方案，使其年总收益最高。

注：个税税率2021

根据国家税务总局发布的最新个税税率表，2021年个税税率分为7级，具体如下：

级数	应纳税所得额（元）	税率（%）	速算扣除数（元）
1	0 - 36000	3	0
2	36000 - 144000	10	2520
3	144000 - 300000	20	16920
4	300000 - 420000	25	31920
5	420000 - 660000	30	52920
6	660000 - 960000	35	85920
7	960000以上	45	181920

速算扣除数

速算扣除数是用于简化计算个人所得税的方法，具体金额根据不同级数而定。速算扣除数的目的是为了减少纳税人缴税的工作量。

论文

基于非线性规划的最优薪金领取方案研究

摘要

本文通过理想化模型，非线性规划模型，设计了如何调整每月的预发金额以及年终一次性发放金额方案，使得一年内个人的总收益最高。该问题的研究为企业和个人，提供税务筹划和个人薪金领取方案，帮助其在合法的前提下进行合理避税，最大化收益。

针对问题一：首先通过直观的分析得出，需均匀分配年终奖奖金以及员工每月工资，使这两项同时达到税率临界点，再去分配个人薪金领取方案，才能最大限度达到合理避税。然后我们计算了年收入多少时，达到三档率上限。得到年收入与纳税额的关系，从而求出二者关系的局部分段函数，由此找到每个年收入对应的税率区间，再代入题中要求的年收入，得出最小纳税结果。最后通过matlab代码遍历奖金范围，输出最小纳税额，对以上结果进行检验。

针对问题二：为解决投资收益率的时效性问题，建立了投资理想化月收益率模型，再由此建立非线性规划模型分析月收益率与相对年收入的关系。得到了给定税前年收入，月薪如何分配以达到相对年收入最高的模型。通过matlab中的非线性规划求解器中的“内点法”进行遍历月收益率增长，可以得到税前年收入为一个确定的值时，相对年收入随月收益率增长，月薪的分配情况。我们给定税前年收入为8万，将月薪分配情况配情况填入了附本80000.xlsx文件。为了观察税前年收入固定时，月收益率在一定区间内，每增长0.01％时，相对年收入平均增长固定值的规律，我们通过matlab一段代码运算出来，在月收益率的变化区间内的分段函数表达式。最后，通过“决定系数"分析方法，对R²进行拟合度分析。

关键词： 理想化模型，非线性规划模型，matlab，分段函数

• 问题重述

1.1问题背景

某公司为适应市场变化并激励长期服务于公司的核心人才，打破了传统的等额月度制度，优化其薪资管理体系。针对在公司连续工作满五年的资深员工，公司引入一项全新的薪资发放选择机制。符合条件的员工可以根据自身的经济需求和规划，向公司财务部门申请工资每月可变额度发放，但须确保任何单月的工资数额不超过其年薪的20%。同时，此机制还需满足半年内的总收入上限，即上半年所获工资总额不得超过年薪的80%。剩余未提前发放的部分将作为年终奖金，在每年年末一次性发放。员工们面临的关键决策在于如何最优化地调整每个月预领工资的数额以及接受年终一次性发放的奖金规模，从而在遵循公司上述规定的前提下，最大限度地提高自己全年度的总体收入水平。

1.2问题提出

针对以下各种情况

问题1 查阅国家个人所得税税率表，为年收入为8万元、12万元、18万元的职员，设计个人薪金领取方案，合理避税，使得一年的税后收入最高。

问题2 部分职员每月可以将80%收入用于投资理财项目，为他们设计个人薪金领取方案，使其年总收益最高。

1.3已知条件

2021年个税税率

根据国家税务总局发布的最新个税税率表，2021年个税税率分为7级，具体如下：

级数	应纳税所得额（元）	税率（%）	速算扣除数（元）
1	0 - 36000	3	0
2	36000 - 144000	10	2520
3	144000 - 300000	20	16920
4	300000 - 420000	25	31920
5	420000 - 660000	30	52920
6	660000 - 960000	35	85920
7	960000以上	45	181920

• 问题分析

2.1 问题一

分配一年年收入在缴纳税后，收入最高的方案，必须在符合法律的前提下进行合理避税。这是合理实施纳税方案的前提。年总收入大于60000的人群，需考虑月工资起征点5000，12个月工资总额需不小于60000，才能最大限度避掉起征点不需要缴纳的税。把纳税总额分为2部分，一部分为十二个月工资总和部分所需上交的税额，另外一部分为年终奖部分所需上交的税额。要使纳税总额最小的就是保证月工资纳税和年终奖纳税总额最少。通过直观的分析，企业发放年终奖奖金以及员工每月工资的不均衡发放，必然导致个人所得税税负提高，实际到手的收入减少。每月均匀发放工资薪金会降低个人所得税的税率，会减少应纳个人所得税金额。企业在发放年终一次性奖金时，应抓住税率临界点。本方案即在寻找这个税率的临界点。

根据2021年中国个人所得税税率表，我们为不同年收入水平的职员制定相应的薪金领取方案以合理避税，使一年的税后收入最高：

年收入8万以及12万的职员：

年收入为8万以及12万时，需满足十二个月应纳税所得额总和不超过36000，且剩余年终奖也满足应纳税所得额不超过36000的情况时。总纳税额最小，年总收益最高。

年收入18万元的职员：

年收入为18万时，需满足十二个月应纳税所得额总和不超过144000，且剩余年终奖也满足应纳税所得额不超过36000的情况时。总纳税额最小，年总收益最高。

2.2 问题二

分配个人薪金领取方案，需要兼顾税收节省与投资收益的双重目标，使其最大限度的在每年年末总收益最高。

收益最高，首先要保证投资的本金达到最大值，也就是每月收入的80%全部都用来投资理财项目。而每个月的收入是不固定的，又考虑到每月工资发放额度不超过年收入20%，前半年收入不超过年收入的80%。所以既要让工资早并且多的拿到手里，还要考虑到薪金领取限制条件和避税问题。

在避税方面还需考虑如何能充分利用税收优惠政策，又能保障投资收益最大化的平衡点。使得盈利达到一个区间时，每月拿多少工资减去缴纳的税，可以使收益最大。又或是利率在达到一个值时，远远大于本金所需缴纳的税，此情况就要月薪金领取方案达到最大限制条件（即不需要考虑纳税金额）。再或是利率低于某一个值时，所需缴纳的税大于盈利，此时就与第一问的薪金领取方案所考虑的一致，需保证在最大程度避税的前提下，稳定取得较小投资收益。

投资理财产品需考虑理财产品的风险、收益率、回报率、流动性等。如股票债券，有时会上涨100%，有时会下跌300%；国债是相对来说很稳定的收益，全年活期收益率稳定在一个数值上下为浮动，基本不会超过1%；银行利息时最有保障最低收益的一种。并且还要考虑到像国债与银行存款等都分为死期与活期存款，死期又分三月期、六月期、全年期等。

还需考虑投资产品的风险程度及职员自身的现金流需求。若投资产品风险较高，建议预留一定比例的月度工资作为安全缓冲，以确保日常生活不受影响。这里务必注意投资市场的波动性和不确定性，不能单纯为了追求避税而忽略投资风险。

最后，考虑到投资收益率的时效性，我们建立了一个理想化模型，便于计算出年收入不同的收益额是多少。

• 模型假设

3.1问题假设

1. 假设我们遵循2021年中国个人所得税税率表和年终奖的单独计税规则，年终奖采用一次性计税方式。

2. 假设本题中设计个人薪金领取方案不同年收入的职员的任职时间均满五年，员工已知其年收入，并且他们可以灵活调整每月工资发放额度，但不得超过年收入的20%，并且前6个月的累计收入不得超过年收入的80%。职员通过调整月度工资和年终奖发放比例，最大程度地减少个人所得税负担，从而提高全年税后收入。

3. 假设这部分职员将每月收入的80%投入投资理财项目。

4. 假设员工的生活开销可以从月度工资中得到充分满足，调整工资领取方案不影响正常生活需求，且不会产生额外借贷成本。

5. 假设不用考虑可以税前扣除的基本养老保险金、住房公积金和住房补贴，实际操作时应作为纳税筹划因。

3.2 理想化模型假设

1. 月收益率稳定性：假设每个月的收益率固定且一致，忽略实际市场中收益率可能出现的波动性，即不论市场条件如何变化，每个月的收益率始终不变。

2. 无复利效应：假设每个月产生的投资收益不会再次投资从而产生额外收益。

4. 无交易成本和税费：假设投资不计入交易成本，如手续费、管理费等，也不考虑税费对投资收益的影响。

5. 风险性：假设无投资风险，月收益率≥0。

6. 市场效率：假设投资收益不受市场波动的影响，所有投资者都能获得同样的固定收益率。

7. 月收益率变化区间 [0.00%,100.00%]

• 符号说明

符号	意义	单位
T	年总纳税额	元
P	税前年收入	元
X	月收益率	/
Xt	t月税前工资（即月薪）	元
Xt′	t月所需缴纳的税	元
(Xt- Xt′)	每个月投资本金	元
A	税前年终奖	元
A′	年终奖所需缴纳税	元
M	相对年收入	元
Z	年总收入	元

• 模型的建立与求解

5.1 问题一模型的建立与求解

研究年收入与应纳税额关系，首先根据题意，将年收入分为年终奖和十二个月工资总和来看，结合个税税率表我们发现：

当每月应纳税所得额恰好达到起征点时，起征点=5000*12=60000，即年收入≤60000时不需要缴纳税额；

当年终奖和十二个月的工资总合均恰好达到第一级税率上限时，年终奖应纳税所得额为36000，十二个月的工资总合应纳税所得额为8000*12=96000，即60000＜年收入≤132000时应缴纳所得税需缴纳3%的税。

当年终奖和十二个月的工资总合均恰好达到第二级税率上限时，年终奖应纳税所得额为144000，十二个月的工资总合应纳税所得额为17000*12=204000，即132000＜年收入≤348000时应缴纳所得额需缴纳10%的税，再减去第二级的速算扣除数。

以此类推，因为本题年收入不涉及到第二级税率之后的税率，所以之后的节点在这里不进行计算。

基于上述发现，处于这几个节点之内的年收入，只需确保分配年终奖与十二个月每月的月工资都不超过对应节点的税率级数，以及在月工资、前半年工资发放符合题目约束条件下，可任意分配。节点计算结果如表1所示

表1 特殊年收入节点明细

年收入	12个月工资总和	年终奖	纳税总额
60000	60000	0	0
132000	96000	36000	2160
348000	204000	144000	23760

取其变化趋势展示如图1：

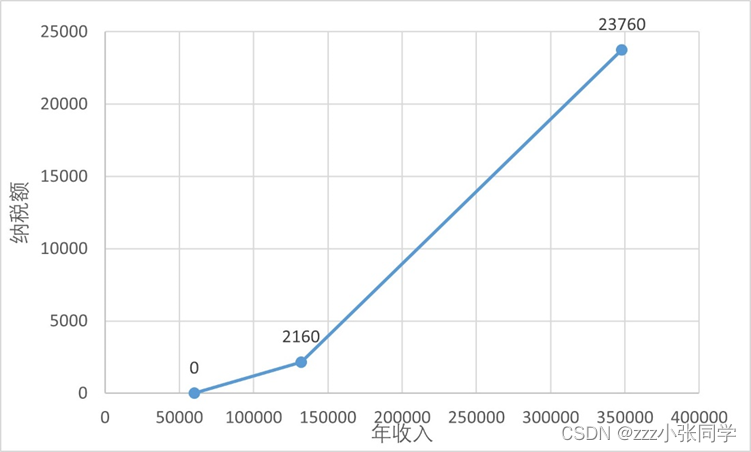
图1

由上述图表可以看出，年收入在60000~132000之间，纳税额较缓慢增长；年收入达到132000以后，纳税额较急速增长。观察可得年收入与纳税额的关系符合分段函数的特点，且前后两段均为一次函数。

因此带入点的坐标，得到的分段函数表达示为：

公式1

其中，年总纳税额为T，税前年收入为P

将8万、12万、18万带入对应的分段函数表达式中，得到其对应的所需缴纳的税额分别为600、1800、6960。

据分段函数与图表分析，年收入为8万以及12万时，十二个月应纳税所得额和年终奖应纳税所得额都位于第一级税率范围内，即年收入全额适用3%的税率时，总纳税额最小，年总收益最高。年收入为18万时，十二个月应纳税所得额和年终奖应纳税所得额都位于第二级税率范围内时，即年收入全额适用10%的税率时，总纳税额最小，年总收益最高。

满足此情况的个人薪金领取方案有无数种，我们针对每月工资平分，设计了以下个人薪金领取方案。 设计方案如下表2：

表2合理避税一年后个人薪金领取方案

年收入（元）	80000	120000	180000
纳税额（元）	600	1800	6960
每月月工资（元）	5000	8000	12000
年终奖（元）	20000	24000	36000
年总收益（元）	79400	118200	173040

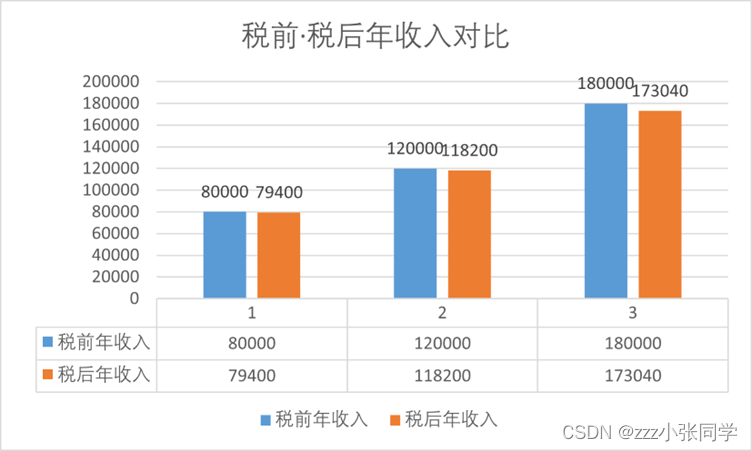最后我们使用簇状柱形图来直观展示8万、12万、18万税前税后年收入的对比，如图2：

图2

我们针对以上总纳税额最小的情况编写了matlab代码。通过输入年收入totalIncome，遍历奖金范围从而寻找最优税收组合，即可输出总纳税额最小minTax元。

5.2 问题二模型的建立与求解

运用非线性规划模型对月收益率与年收入的关系进行分析。考虑到投资收益率的时效性，我们建立了一个投资理想化月收益率模型，便于分配月工资以得到最佳薪金领取方案。

非线性规划的思路是： 随着月收益率由0.00%到100.00%的变化，月工资分配是自变量，相对年收入是因变量。采取给定税前年收入8万，计算月薪如何分配以达到相对年收入最高的方案。优化目标为得到最优个人薪金领取方案，优化目标函数为：

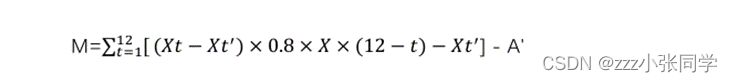
公式2

其中，月收益率为X，投资额度为每月工资的80%，t月税前工资（即月薪）为Xt，t月所需缴纳的税为Xt′， 每个月投资本金为(Xt- Xt′)，年终奖纳税前为A，年终奖所需缴纳的税为A′，相对年收入为M，年总收入Z，税前年收入为P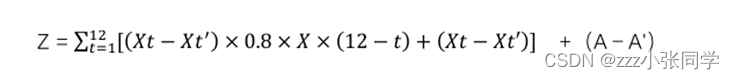

公式3

公式4

约束如下

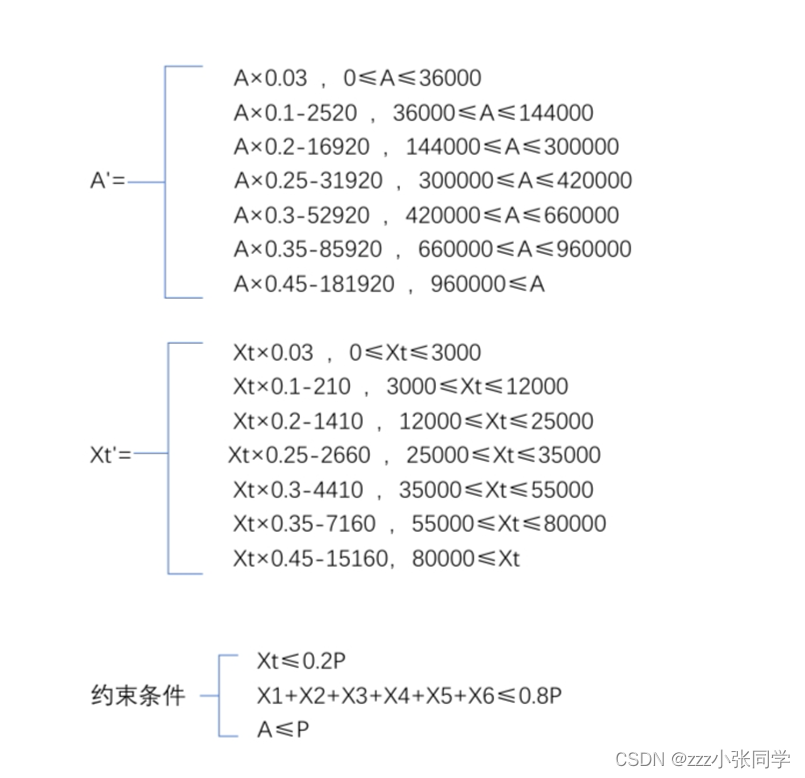
关于约束条件的说明： 每月工资发放额度不超过年收入 20%

前半年收入不超过年收入的 80%。

税前年终奖不应超过税前年收入。

因为本题年总收入和月收益率都是变化的，所以我们带入了年收入8万、12万、18万，借助matlab遍历月收益率增长，计算不同月薪分配方案，和相应的税后收入和投资收益，可以得到关于8万、12万、18万相对年收入，随月收益率增长，月薪分配情况见附录

我们使用matlab中的非线性规划求解器中的“内点法“进行求解，了解到该方法的原理是将所有可能值依次代入，求出符合约束的最优解，因此会出现与实际值偏差较大的离群点，所以我们进行剔除离群点操作后，再通过采用“均值替补法”对空数据进行补充。

观察月收益率由0每次增长0.01个百分点，一直增长到100个百分点这段图像。我们发现：税前年收入固定时，月收益率在一定区间内，每增长0.01%时，相对年收入平均增长固定值。此时个人薪金如何领取能达到相对年收入最大。

我们通过matlab利用非线性回归模型根据前面所述约束条件和纳税计算规则敲写代码（详见附录2.1代码），生成年收入8万、12万、18万在不同收益率下最优薪金领取方案表格，详见附件1、附件2、附件三。

下表是税前年收入8万时，我们通过matlab一段代码运算出来（附录几），在不同月收益率的变化区间内的一次函数表达式，展示的规律为税前年收入固定时，月收益率在一定区间内，每增长0.01％时，相对年收入平均增长固定值。

表3

区间	函数
0.00%~0.78%	y = 390512.82x-600.00
0.78%~0.96%	y = 394444.44x-630. 67
0.96%~1.26%	y = 403479.25x-717.49
1.26%~1.41%	y = 411447.70x-817.89
1.41%~1.45%	y = 452146.41x-1391.74
1.45%~1.70%	y = 456699.71x-1457.76
1.70%~1.77%	y = 460399.32x + -1520.66
1.77%~2.08%	y = 487449.41x-1999.44
2.08%~3.83%	y = 498519.71x-2229.71
3.83%~4.31%	y = 503967.88x-2438.37
4.31%~5.95%	y = 506156.62x-2532.71
5.95%~14.11%	y = 514510.12x-3029.74
14.11%~21.27%	y = 515999.40x-3239.88
21.27%~25.03%	y = 516975.94x-3447.59
25.03%~62.50%	y = 518984.55x-3950.34

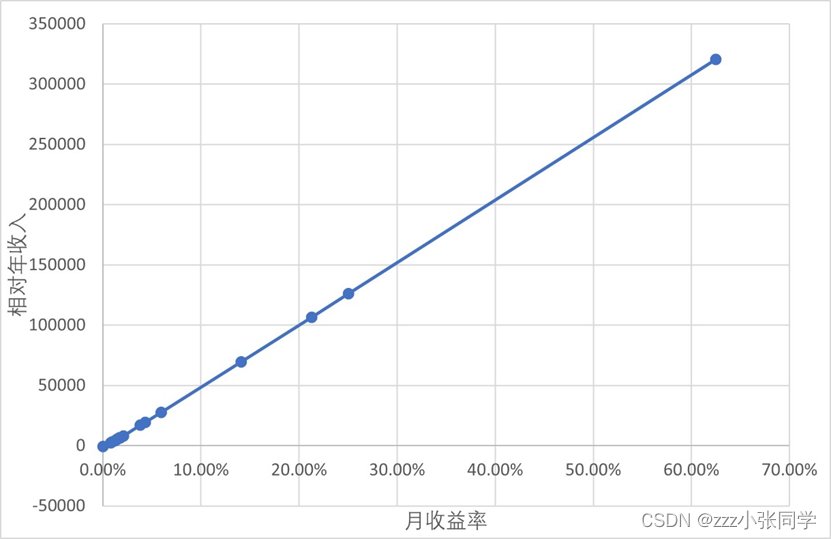
取其变化趋势展示如图X

图

• 模型检验

6.1问题一的检验

在matlab解决问题一的代码中依次将年收入（totalIncome）输入为8万、12万、18万，遍历奖金范围从0到年收入（totalIncome）从而输出总纳税额最小（minTax）元依次为600、1800、6960。对照函数图像x上相对应的点相同，由此可见分段函数模型的准确性。

6.2问题二的检验

为检验模型的准确性，“决定系数"分析方法，我们对R²进行拟合度分析

从1万个点中随机抽取了1000个数据计算残差

得到残差图如下

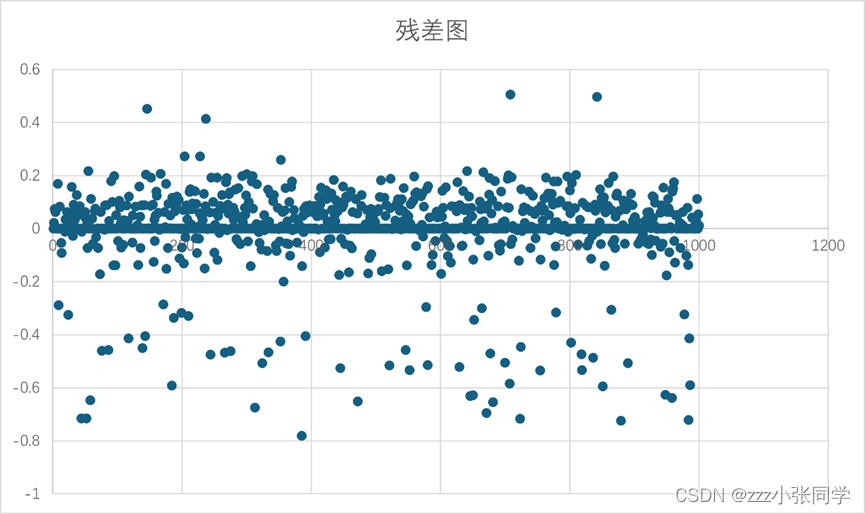
图X

我们可以直观地看出，绝大部分点的上下波动不超过0.2。

而后我们计算10000个数据的总残差平方和：

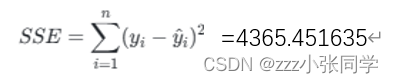
总平方和：

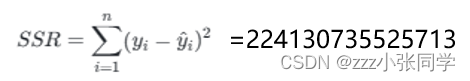
决定系数：

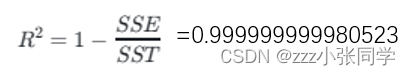
其中R^2几乎等于1

说明模型基本符合所求。

• 模型的评价与推广

7.1模型的评价

7.1.1理想化模型

7.1.1.1模型的优点

1.有效性：能够反映所研究的问题核心要素为月收益率的变化与合理避税问题如何影响个人薪金领取方案，排除次要因素的影响，如无交易成本和税费，从而提炼出简洁且普适的规律。

2.简洁性：具备高度的简化性，去除不必要的细节，保留最重要的变量（月收益率的变化）和参数，以便于理解、分析、解决问题。

3.实用性：足够实用，能够在实际的合理避税问题方面提供一定指导。能够帮助人们更好地了解国家税收政策，并且合理避税。

4. 极限性：考虑到月薪分配的边界条件和极限情况，使模型在极端条件下依然能够得出合理并且符合限制条件的运算结果。

7.1.1.2模型的缺点

为了便于理解和解析问题，我们忽略掉不同理财产品具有不同的收益率，不考虑投资风险以及收益率是实时变化的情况，同时也不考虑投资收益再次投资从而产生额外收益的情况。

7.1.1.3模型的改进

在简化收益率模型的基础上，考虑更多影响因素，如考虑到投资收益会再次投资从而产生二次、三次收益等，以提高模型的现实贴合度。

在理想化模型中加入一些不确定因素分析，使个人薪金领取方案更具有现实参考性。

7.1.2非线性模型

7.1.2.1模型的优点

1. 能够准确地模拟复杂的税率体系，包括阶梯税率、扣除限额等各种非线性因素，这对于确定最优薪酬结构至关重要。

2. 全局优化：寻找个人所得税最小化的全局最优解，而非仅仅局限于某一局部最优解。

3. 灵活调整：当税率政策、个税起征点、扣除标准等因素发生变化时，模型可以迅速调整参数，重新进行优化，帮助个人制定出最新的最优薪酬领取策略。

4. 综合考虑多种收入类型：在实际薪酬发放中，可能涉及工资、奖金、福利、股票期权等多种形式的收入，每种收入类型的计税方式往往不同，非线性规划模型可以将不同的税收效应整合到一个模型中进行整体优化。

5.  建立模型之前，对附件中的数据进行了预处理，补充了缺失数据，校正了个别错误数据，建立了各类数据之间的联系，找出其规律，便于分析解决问题。

6. 文所有的数据处理均经过精确的分析、比对、效验，具有很强的准确性，真实性；模型求解结果进行了检验，可信度高，可靠性强。

7. 模型求解用到MATLAB、Excel 等多种软件，使求解过程更清晰、专业，运用多种绘图使得数据表达更加清晰明了

综上，非线性模型既能精细刻画实际情况，又能高效寻优，从而帮助企业和个人在合法合规的前提下，最大程度地减少税收负担。

7.1.2.2模型的缺点

模型需要持续跟踪政策动态，并随之更新。虽然强调的是“合理避税”，但在实际操作过程中，即便利用模型找出的方案仍可能存在模糊地带，容易触碰法律红线，造成不必要的税务争议和风险。

matlab非线性求解器使用内点法，容易陷入局部最优解，导致结果与实际有较大的偏差。需要引入其他方法，对模型中的自变量进行精细调整和优化，确保模型在处理具体问题时具有更高的预测精度。

7.1.2.3模型的改进

可以提炼关键因素和假设条件，适度的去简化模型，使其易于理解和求解。在模型中考虑除税收外的其他重要因素，比如社会保障、退休计划、员工激励效果等。多目标优化，使薪金领取方案在降低税负的同时，也能满足企业的激励需求和员工的期望。根据具体情境设定更多的约束条件，使模型更贴近实际情况。

7.2模型的推广

问题中建立的理想化模型，非线性规划模型贴近实际，适用于对合理避税分配薪资发放问题的分析与预测，有着广泛的通用性和借鉴意义，模型可操作性强，值得推广。

对于企业或个人而言，利用税收理想化模型，在合法合规的前提下进行税务筹划或调整个人薪金领取方案，在实际操作中能合理避税，最大化收益。

附录

1.1代码（matlab）
计算最少税收的薪资分配方案及其纳税额
%定义总收入（totalIncome）和个税起征点（taxThreshold）、最优税收（minTax）、月缴税（monthlyTax）
% 定义参数
totalIncome = 180000; % 税前年收入
taxThreshold = 5000; % 个税起征点（每月）
% 初始化变量
minTax = inf; % 最小税收值初始设为正无穷大
monthlyTax = 0; % 月工资缴税初始为空
salary=0;
% 遍历奖金范围寻找最优税收组合
for bonus = 0:totalIncome
% 计算月工资
salary = (totalIncome - bonus) / 12;
% 计算月工资对应的税收
if salary > taxThreshold
taxableSalary = salary - taxThreshold;
if taxableSalary < 3000
monthlyTax = taxableSalary * 0.03;
elseif taxableSalary < 12000
monthlyTax = taxableSalary * 0.1 - 210;
elseif taxableSalary < 25000
monthlyTax = taxableSalary * 0.2 - 1410;
elseif taxableSalary < 35000
monthlyTax = taxableSalary * 0.25 - 2660;
elseif taxableSalary < 55000
monthlyTax = taxableSalary * 0.3 - 4410;
elseif taxableSalary < 80000
monthlyTax = taxableSalary * 0.35 - 7160;
else % taxableSalary > 80000
monthlyTax = taxableSalary * 0.45 - 15160;
end
else
monthlyTax = 0;
end
% 计算年终奖对应的税收
annualBonus = bonus;
if annualBonus > 0
taxableBonus = annualBonus;
if taxableBonus < 36000
bonusTax = taxableBonus * 0.03;
elseif taxableBonus < 144000
bonusTax = taxableBonus * 0.1 - 210;
elseif taxableBonus < 300000
bonusTax = taxableBonus * 0.2 - 1410;
elseif taxableBonus < 660000
bonusTax = taxableBonus * 0.25 - 2660;
else % taxableBonus > 660000
bonusTax = taxableBonus * 0.45 - 15160;
end
else
bonusTax = 0;
end
% 计算并更新年度总税收
annualTax = monthlyTax * 12 + bonusTax;
% 如果当前税收小于已记录的最小税收，则更新最优税收
if annualTax < minTax
minTax = annualTax;
end
end
% 输出最佳税收分配结果
fprintf('最佳情况总的税收值: %.2f\n', minTax);

2.1代码（matlab）
计算一定工资下，月收益率增长所对应的分配方案以及相对年收入
D=zeros(15);
zonggongzi=180000;   
for i=0:0.0001:1
global shouyilv;
shouyilv = i
A = [1 1 1 1 1 1 0 0 0 0 0 0 0];
B = zonggongzi * 0.8;
aeq=[1 1 1 1 1 1 1 1 1 1 1 1 1 ];
beq=zonggongzi;
lb=[0,0,0,0,0,0,0,0,0,0,0,0,0];
ub=[zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi*0.2;
    zonggongzi
    ];
x0=[zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi*0.2,zonggongzi];

options = optimoptions('fmincon', 'Algorithm', 'interior-point','ConstraintTolerance', 1e-10,'MaxFunctionEvaluations', 100000000000000000000);
[x,fval] = fmincon(@nianshouyi,x0,A,B,aeq,beq,lb,ub,[],options); % 使用 options 结构作为额外参数

C=[shouyilv fval x];
D=[D;C];

end

% 指定Excel文件名
excelFileName = 'Example3.xlsx';

% 使用writematrix函数将数值数组写入Excel文件
writematrix(D, excelFileName);

function f = nianshouyi(x)
global shouyilv;
gongzinashui=zeros(12);
touzishouyi=zeros(12);
nashuihougongzi=zeros(12);
for i=1:12
if x(i)<5000
gongzinashui(i) = 0;
elseif x(i) <= 8000
gongzinashui(i) = (x(i)-5000) * 0.03;
elseif x(i) <= 17000
gongzinashui(i) = (x(i)-5000) * 0.1 - 210;
elseif x(i) <= 30000
gongzinashui(i) = (x(i)-5000) * 0.2 - 1410;
elseif x(i) <= 40000
gongzinashui(i) = (x(i)-5000) * 0.25 - 2660;
elseif x(i) <= 60000
gongzinashui(i) = (x(i)-5000) * 0.3 - 4410;
elseif x(i) <= 85000
gongzinashui(i) = (x(i)-5000) * 0.35 - 7160;
else
gongzinashui(i) = (x(i)-5000) * 0.45 - 15160;
end
nashuihougongzi(i)=x(i)-gongzinashui(i);
touzishouyi(i)=nashuihougongzi(i)*0.8*shouyilv*(12-i);
x(i)=touzishouyi(i)-gongzinashui(i);
end

if x(13) <= 36000
nianzhongjiangnashui = x(13) * 0.03;
elseif x(13) <= 144000
nianzhongjiangnashui = x(13) * 0.1 - 2520;
elseif x(13) <= 300000
nianzhongjiangnashui = x(13) * 0.2 - 16920;
elseif x(13) <= 420000
nianzhongjiangnashui = x(13) * 0.25 - 31920;
elseif x(13)<= 660000
nianzhongjiangnashui = x(13) * 0.30 - 52920;
elseif x(13)<= 960000
nianzhongjiangnashui = x(13) * 0.35 - 85920;
else
nianzhongjiangnashui = x(13) * 0.45 - 181920;
end
x(13)=-nianzhongjiangnashui;

f=-sum(x);
end

2.2代码（matlab）
计算函数表达式
%% 设置导入选项并导入数据
opts = spreadsheetImportOptions("NumVariables", 2);

% 指定工作表和范围
opts.Sheet = "Sheet2";
opts.DataRange = "A1:B17";

% 指定列名称和类型
opts.VariableNames = ["VarName1", "VarName2"];
opts.VariableTypes = ["double", "double"];

% 导入数据
S1 = readtable("E:\MATLAB\R2023a\bin\80000.xlsx", opts, "UseExcel", false);

%% 转换为输出类型
S1 = table2array(S1);

%% 清除临时变量
clear opts

for i=1:16
% 已知两个点的坐标
x1 = S1(i,1);
y1 = S1(i,2);
x2 = S1(i+1,1);
y2 = S1(i+1,2);

% 计算斜率 m
m = (y2 - y1) / (x2 - x1);

% 计算y轴截距 b
b = y1 - m * x1;

% 显示一次函数的表达式
fprintf('第%d段: y = %f*x %f\n',i, m, b);

end


2.3.1代码（matlab）
选取1000个数据计算残差
%% 设置导入选项并导入数据
opts = spreadsheetImportOptions("NumVariables", 2);

% 指定工作表和范围
opts.Sheet = "Sheet1";
opts.DataRange = "A3:B10002";

% 指定列名称和类型
opts.VariableNames = ["VarName1", "VarName2"];
opts.VariableTypes = ["double", "double"];

% 导入数据
Untitled = readtable("E:\MATLAB\R2023a\bin\80000.xlsx", opts, "UseExcel", false);

%% 转换为输出类型
Untitled = table2array(Untitled);

%% 清除临时变量
clear opts


e = zeros(1, 1000); % 初始化残差数组

for l=1:1000
x = randi([1, 10000], 1, 1);
c=x;
x=x/10000;
if x<0.0078
y = 390488.283505*x -600.000000;
elseif x<0.0096
y = 394500.454141*x -631.294931;
elseif x<0.0126
y = 403479.251638*x -717.491387;
elseif x<0.0141
y = 411447.704867*x -817.893898;
elseif x<0.0145
y = 452146.415812*x -1391.745722;
elseif x<0.0170
y = 456699.718246*x -1457.768607;
elseif x<0.0177
y = 460399.320019*x -1520.661837;
elseif x<0.0208
y = 487449.417579*x -1999.448564;
elseif x<0.0383
y = 498519.718725*x -2229.710828;
elseif x<0.0431
y = 503967.881965*x -2438.375480;
elseif x<0.0595
y = 506156.626476*x -2532.710369;
elseif x<0.1411
y = 514510.122171*x -3029.743362;
elseif x<0.2127
y = 515999.401217*x -3239.880636;
elseif x<0.2503
y = 516975.947511*x -3447.592033;
elseif x<0.6250
y = 518984.553957*x -3950.346226;
else
y = 519784.000008*x -4450.000008;
end

y1=Untitled(c,2);
e(l)=y1-y;
end
% 指定Excel文件名
excelFileName = 'cancha.xlsx';

% 使用writematrix函数将数值数组写入Excel文件
writematrix(e, excelFileName);


2.3.2代码（matlab）
计算所有数据的残差
%% 设置导入选项并导入数据
opts = spreadsheetImportOptions("NumVariables", 2);

% 指定工作表和范围
opts.Sheet = "Sheet1";
opts.DataRange = "A3:B10002";

% 指定列名称和类型
opts.VariableNames = ["VarName1", "VarName2"];
opts.VariableTypes = ["double", "double"];

% 导入数据
Untitled = readtable("E:\MATLAB\R2023a\bin\80000.xlsx", opts, "UseExcel", false);

%% 转换为输出类型
Untitled = table2array(Untitled);

%% 清除临时变量
clear opts

e = zeros(1, 10000); % 初始化残差数组

for l=1:10000

x=l/10000;
if x<0.0078
y = 390488.283505*x -600.000000;
elseif x<0.0096
y = 394500.454141*x -631.294931;
elseif x<0.0126
y = 403479.251638*x -717.491387;
elseif x<0.0141
y = 411447.704867*x -817.893898;
elseif x<0.0145
y = 452146.415812*x -1391.745722;
elseif x<0.0170
y = 456699.718246*x -1457.768607;
elseif x<0.0177
y = 460399.320019*x -1520.661837;
elseif x<0.0208
y = 487449.417579*x -1999.448564;
elseif x<0.0383
y = 498519.718725*x -2229.710828;
elseif x<0.0431
y = 503967.881965*x -2438.375480;
elseif x<0.0595
y = 506156.626476*x -2532.710369;
elseif x<0.1411
y = 514510.122171*x -3029.743362;
elseif x<0.2127
y = 515999.401217*x -3239.880636;
elseif x<0.2503
y = 516975.947511*x -3447.592033;
elseif x<0.6250
y = 518984.553957*x -3950.346226;
else
y = 519784.000008*x -4450.000008;
end

y1=Untitled(l,2);
e(l)=y1-y;
end
% 指定Excel文件名
excelFileName = 'cancha.xlsx';

% 使用writematrix函数将数值数组写入Excel文件
writematrix(e', excelFileName);