例题一

解法(暴⼒解法 -> 贪⼼):
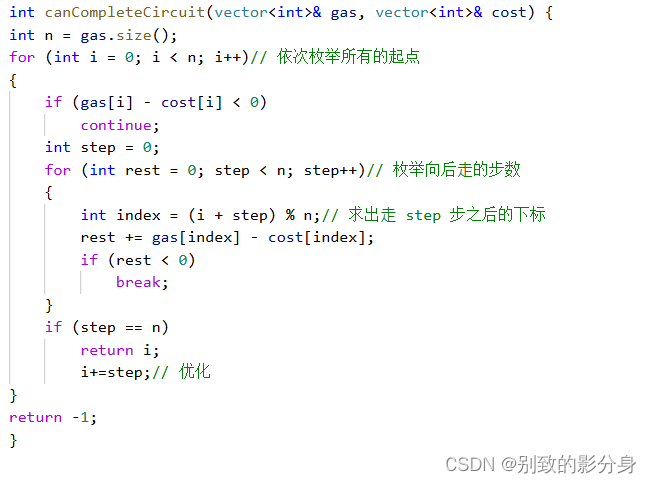
暴⼒解法:
a.
依次枚举所有的起点;
b.
从起点开始,模拟⼀遍加油的流程
贪⼼优化:
我们发现,当从
i
位置出发,⾛了
step
步之后,如果失败了。那么
[i, i + step]
这个区间内任意⼀个位置作为起点,都不可能环绕⼀圈。因此我们枚举的下⼀个起点,应该是 i + step + 1
。
例题二

解法(贪⼼):
假设我们有⼀个数 n,它有m位数字,每⼀位数字分别是
d1,d2,......,dm
。
我们想要修改这个数字,使得修改后的结果既⼩于原数字 n ,⼜满⾜单调递增和最⼤化。为了实现这个⽬标,我们需要将不满⾜递增的⾼位数字尽可能地减⼩。
⾸先,我们需要找到⼀个位置 k,使得 d
1
≤
d
2
≤...≤
d
k
>
d
k
+1...(例如:12335412,k=4,d
k=5)。这个位置 k 表⽰从⾼到低,第⼀个不满⾜单调递增的数字的位置。我们需要将这个数字减1,因为这是最⼩的减⼩量。
接下来,我们需要将低位数字都修改为9,这样可以保证修改后的数字是最⼤的,并且还能保证单调递增。修改后存在以下两种情况:
1.
如果d
k
−1
<
dk ,则修改后的数字满⾜d
1
≤
d
2
≤ ... ≤ (
d
k − 1) ≤ 9 ≤ ... ≤ 9 。这是因为
dk在减1的同时,低位数字被修改为 9。
2. 如果 d k −1 = dk,则修改后的数字满⾜ d 1 ≤ ... ≤ d k −1 > ( d k − 1) ≤ 9 ≤ ... ≤ 9。在这种情况下,我们仍然保证了低位数字的最⼤化和单调递增,但是可能会出现⾼位数字不再单调递增的情况。
2. 如果 d k −1 = dk,则修改后的数字满⾜ d 1 ≤ ... ≤ d k −1 > ( d k − 1) ≤ 9 ≤ ... ≤ 9。在这种情况下,我们仍然保证了低位数字的最⼤化和单调递增,但是可能会出现⾼位数字不再单调递增的情况。
第⼆种情况需要继续修改这个数字。我们需要找到⼀个位置 t ,使得d
1
≤
d
2
≤ ... <
d
t
=
d
t
+1
= ... =
dk。这个位置 t 表⽰从⾼到低,最后⼀个⾼位数字相等的位置。我们需要将dt 减 1,并将之后的所有数字都修改为9,以满⾜d
1
≤
d
2
≤ ... ≤
d
t
− 1 ≤ 9 ≤ ... ≤ 9,即⾼位数字的单调递增和低位数字的最⼤化。
•
例如:1224444361,成功修改后的最⼤值为1223999999。
通过这种修改⽅式,我们可以得到⼀个新的数字,它既⼩于原数字 n,⼜满⾜单调递增和最⼤化。
算法思路:
1.
将整数 n 转换为字符串形式,以便于对其进⾏修改操作,并将其存储在字符串变量 str 中。
2.
初始化⼀个变量 pos,⽤于记录从⾼位到低位第⼀个不满⾜单调递增的数字的位置。初始值为 -1,表⽰在第⼀位之前。
3.
从⾼位到低位遍历字符串 str,寻找第⼀个不满⾜单调递增的数字的位置。当遇到⼀个数字⼩于前⼀个数字时,记录这个位置为 pos,并退出循环。
4.
如果 pos 被更新,说明存在需要修改的数字,执⾏以下操作:
a.
将 pos 位置后的所有数字修改为 9,这样可以保证修改后的数字是最⼤的。
b.
将 pos 位置的数字减⼀,因为这是最⼩的减少量,同时也能够保证修改后的数字仍然⼩于原数
字 n。
c.
检查 pos 前⼀位数字是否⼩于减⼀后的 pos 位置数字,如果⼩于,则说明在 pos 位置之前还有
相同的数字,需要将 pos 前⼀位数字减⼀,并将 pos 位置修改为 9。
i.
重复这个操作,直到 pos 前⼀位数字⼤于等于减⼀后的 pos 位置数字或 pos 已经移动到了第⼀位。
5.
将修改后的字符串 str 转换为整型数字并返回。

例题三

解法(贪⼼):
贪⼼策略:
正难则反:
当「反着」来思考的时候,我们发现:
i.
当
end <= begin
的时候,只能执⾏「加法」操作;
ii.
当
end > begin
的时候,对于「奇数」来说,只能执⾏「加法」操作;对于「偶数」来说,最好的⽅式就是执⾏「除法」操作这样的话,每次的操作都是「固定唯⼀」的。

例题四
解法(排序 + 贪⼼):
贪⼼策略:
a.
先按照区间的「左端点」排序:此时我们会发现,能够合并的区间都是连续的;
b.
然后从左往后,按照求「并集」的⽅式,合并区间。
如何求并集:
由于区间已经按照「左端点」排过序了,因此当两个区间「合并」的时候,合并后的区间:
a.
左端点就是「前⼀个区间」的左端点;
b.
右端点就是两者「右端点的最⼤值」。

例题五

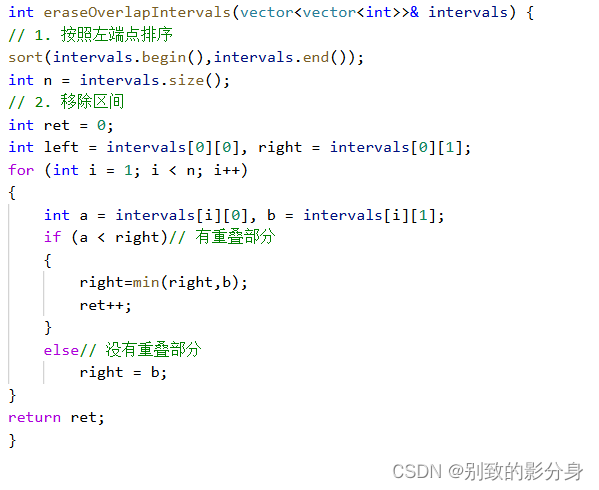
解法(贪⼼):
贪⼼策略:
a.
按照「左端点」排序;
b.
当两个区间「重叠」的时候,为了能够「在移除某个区间后,保留更多的区间」,我们应该把 「区间范围较⼤」的区间移除。
如何移除区间范围较⼤的区间:由于已经按照「左端点」排序了,因此两个区间重叠的时候,我们应该移除「右端点较⼤」的区间.
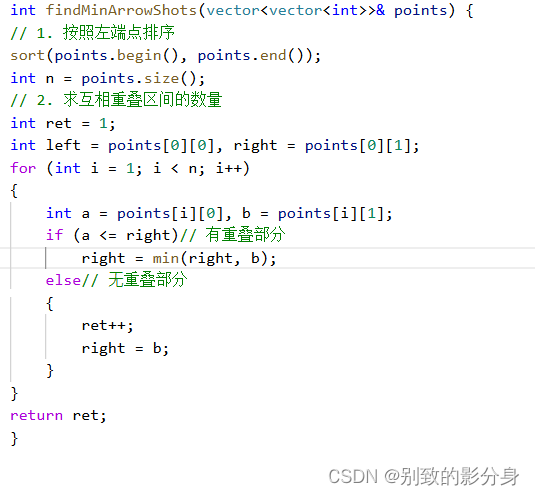
例题六

解法(贪⼼):
贪⼼策略:
a.
按照左端点排序,我们发现,排序后有这样⼀个性质:「互相重叠的区间都是连续的」;
b.
这样,我们在射箭的时候,要发挥每⼀⽀箭「最⼤的作⽤」,应该把「互相重叠的区间」统⼀ 引爆。
如何求互相重叠区间?
由于我们是按照「左端点」排序的,因此对于两个区间,我们求的是它们的「交集」:
a.
左端点为两个区间左端点的「最⼤值」(但是左端点不会影响我们的合并结果,所以可以忽略);
b.
右端点为两个区间右端点的「最⼩值」。