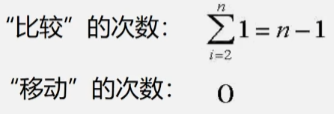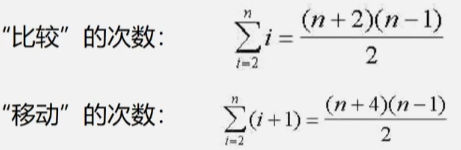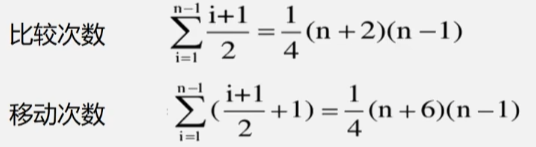文章目录
- 前言
- 1. 直接插入排序
- 直接插入排序算法
- 直接插入排序性能分析
- 2. 折半插入排序
- 3. 希尔排序
- 希尔排序算法
- 希尔排序算法分析
- 排序方法比较
前言
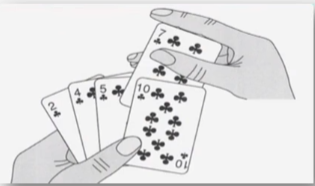
类似于俺们打牌时的插入,每抓来一张牌的时候,就将它放在合适的位置上,插入一张牌之后手里的牌仍然是有序排列的。
基本思想
- 每步将一个待排序的对象,按其关键码大小,插入到前面已经排序号的一组对象的适当位置上,直到对象全部插入为止。
- 即:边插入边排序,保证子序列中随时都是排好序的。
基本操作:有序插入
- 在有序序列中插入一个元素,保持序列有序,有序长度不断增加。
- 起初,a[0] 是长度为 1 的子序列。然后,逐一将 a[1] 到 a[n-1] 插入到有序子序列中。
有序插入方法
- 在插入 a[i] 前,数组 a 的前半段(a[0] ~ a[i-1])是有序段,后半段(a[i] ~ a[n-1])是停留于输入次序的无序段。
- 插入 a[i] 使 a[0] ~ a[i-1] 有序,也就是要为 a[i] 找到有序位置 j(0 <= j <= i),将 a[i] 插入在 a[j] 的位置上。
插入位置
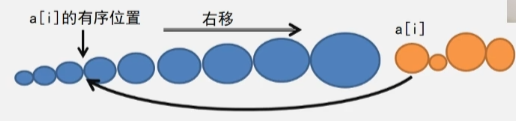
- 插在中间:要插入的 a[i] 元素比前 n 个大,比后 m 个小,将后 m 个元素都后移,将 a[i] 插进去。
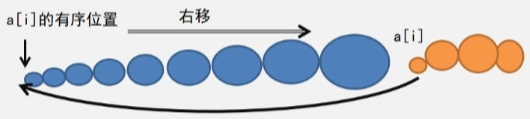
- 插在最前面:要插入的元素 a[i] 比最小的元素都要小比,那最前面的就是他的位置,将所有的元素都后移,将它插进去。
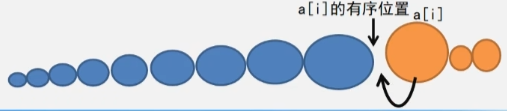
- 插在最后面:要插入的元素比当前所有的已经有序的元素都大,原来的有序序列无序移动,直接在最后插入 a[i] 。
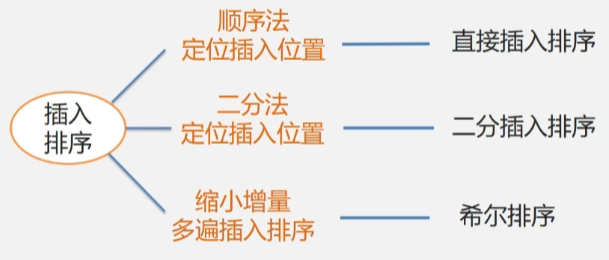
插入排序的种类
1. 直接插入排序
算法步骤
- 设待排序的记录存在数组 r[1…n] 中,r[1] 是一个有序序列。
- 循环 n-1 次,每次使用顺序查找法,查找 r[i](i = 2,…,n)在已排好序的序列 r[1…i-1]中的插入位置,然后将 r[i] 插入表长为 i-1 的有序序列 r[1…i-1],直接将 r[n] 插入表长为 n-1 的有序序列 r[1…n-1],最后得到一个表长为 n 的有序序列。
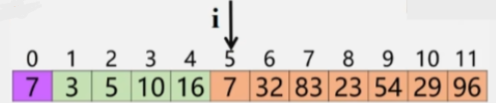
采用顺序查找法查找插入位置
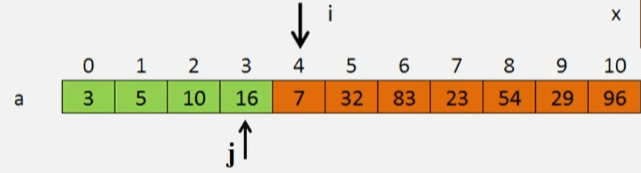
- 假设要将第 i 个位置上的元素插入到绿色的有序序列。
- 查找它的插入位置,然后将插入位置之后的元素往后移动一位,最后才能插入进去。
- 如果直接将后面的元素往后移动的话,4 号位置的元素就会先被覆盖,所以要先将待插入的值存起来。
- 复制插入元素:x = a[i];
- 记录后移,查找插入位置:
- 用一个新的变量来表示当前所查找的位置。
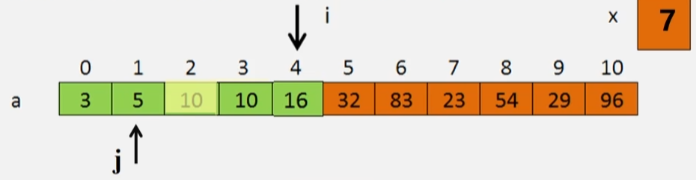
- 用 a[j] 的值来和 x 进行比较,,j 的初始值为 i-1:
- 如果 a[j] > x,说明 x 要插入在 a[j] 之前,然后 a[j] 需要往后移到 a[j+1] 的位置。
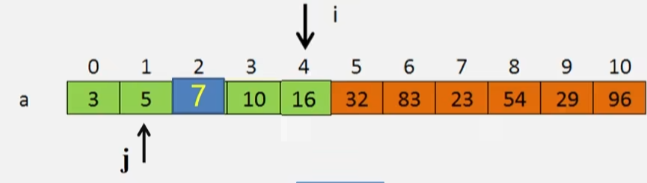
- 一直 j-- 然后和 x 进行比较,直到 a[j] 找到一个小于 x 的值,则将 x 的值 7 存进 j+1 的位置。
- 插入到正确位置:a[j+1] = x
顺序查找法有个明显的问题,每一次查找都要检查数组下标是否越界,每一次循环都要比较两次。
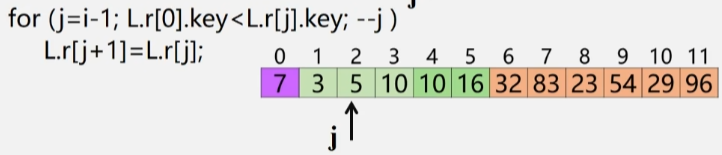
直接插入排序使用 哨兵
- 将要插入的元素复制为哨兵:L.r[0] = L.r[i];
- 记录后移,查找插入位置。
- 插入到正确位置:L.r[j+1] = L.r[0]
- 找到插入位置了以后,直接将哨兵上的元素插入进去。
每一次插入之前,先拿待插入的元素和有序序列的最后一个元素比较一下,如果大于,则不用进行比较,直接插入即可。
用32和16比较,如果大于16则直接查插在最后。
直接插入排序算法
//对顺序表 L 做直接插入排序
void InesrtSort(SqList &L)
{
for(i=2;i<=L.length;i++)
{
if(L.r[i].key<L.r[i-1].key) //小于,则则需将r[i]插入有序子表
{
L.r[0] = L.r[i]; //将待插入的记录暂时存到监视哨中
L.r[i] = L.r[i-1]; //r[i-1]后移
for(j=i-2;L.r[0].key<L.r[j].keylj--) //从后向前寻找插入位置
{
L.r[j+1] = L.r[j]; //记录逐个后移,直到找到插入位置
}
L.r[j+1] = L.r[0]; //将哨兵r[0]即原来的r[i],插入到正确位置
}
}
}
直接插入排序性能分析
实现排序的基本操作有两个:
- 比较序列汇总两个关键字的大小。
- 移动记录(数据元素)。
最好的情况
- 关键在在记录序列汇总顺序有序。
- 和有序序列最后一位比较的时候发现,直接比最后一位大,无须移动。
最坏的情况
- 关键字在记录序列中逆序有序。
- 要插入的每个元素需要和所有的元素进行比较。
平均的情况
时间复杂度结论
- 原始数据越接近有序,排序速度越快。
- 最坏情况下(输入数据是逆序有序的):Tw(n) = O(n2)。
- 平均情况下,耗时差不多是最坏情况的一半:Te(n) = O(n2)。
- 要提高查找速度:
- 减少元素的比较次数。
- 减少元素的移动次数。
2. 折半插入排序
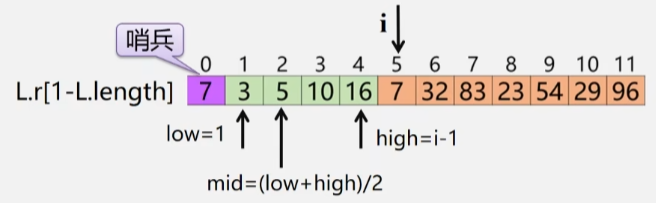
- 先将第 i 个位置的元素保存到哨兵中,在被插入的区域进行折半查找,
- 用中间值与 i 进行比较,如果 mid < i 则 high = mid-1在右半区找。
- 如果 mid > i,则在左半区找,low = mid+1。
- 如果最后找到正确位置,则将插入位置之后的元素往后移动,将哨兵里存的值插进去。
- 如果找了半天,结果在哨兵中才找到想要的结果,则说明找不到了。
算法描述
//对顺序表L左折半插入排序
void BInsertSort(SqList &L)
{
for(i=2;i<=L.length;i++)//依次插入第2~第n个元素
{
L.r[0] = L.r[i];//将待插入的元素存到哨兵位置
low = 1;high = i-1;//设置查找区间初值
while(low <= high)//采用二分查找法查找插入位置
{
mid = (low + high) / 2
if(L.r[0].ley < Lr[mid].key)//要在左半区间找
{
high = mid - 1;
}
else //在右半区间找
{
low = mid + 1;
}
}
//循环结束,high+1为插入位置
for(j = i-1;j>=high+1;j--)
{
L.r[j+1]=L.r[j];//将插入位置之后的元素往后移动
}
L.r[high+1]=L.r[0];//将r[0]即原r[i],插入到正确位置
}
}
算法分析
- 折半查找比顺序查找块,所以折半插入排序就平均性能来书比直接插入排序更快。
- 它所需要的关键码比较次数与待排序对象序列的初始排列无关,仅依赖于对象个数。在插入第 i 个对象时,需要经过 log₂i + 1 次关键码比较,才能确定它应该插入的位置。
- 当 n 较大时,总关键码比较次数比直接插入排序的最坏情况要好的多,但是比其最好情况要差;
- 在对象的初始排列已经被关键码排好序或接近有序时,直接插入排序比折半插入排序执行的关键码比较次数要少;
- 折半插入排序的对象移动次数与直接插入排序相同,依赖于对象的初始排列。
- 减少了比较次数,但没有减少移动次数。
- 平均性能优于直接插入排序。
3. 希尔排序
基本思想
- 先将整个待排序记录序列分隔成若干个子序列,分别进行直接插入排序,待整个序列中的记录基本有序时,再对全体记录进行一次直接插入排序。
希尔排序特点
- 缩小增量。
- 多遍插入排序。
举个例子
- 现有一组无序的初始数据
- 在插入排序的时候选择增量为 5 ,将这样一组数据以 5 个为一组,分成若干子序列。
- 在进行插入排序的时候,先让这三个元素进行比较,比较完之后交换位置。
- 交换完位置之后,这三个元素就离他们最终的位置比较近了。
- 之后就是在这 5 间隔分成的子序列中,每次都挑三个元素来进行比较和交换位置。
- 在 5 间隔插入排序完成之后,每个元素都在它们自己的组内有序。
- 这样就可以让元素一次移动的位置比较大,快速接近最终位置。
- 下一次就进行 3 间隔的排序,将这个序列 3 个为一组,分成若干个子序列。
- 让这些 3 间隔的元素再进行比较然后交换位置(蓝跟蓝比,粉跟粉比,绿跟绿比)。
- 最后再做一遍 1 间隔的排序(就是直接插入排序)。
- 此时这些数据元素已经基本有序了,再进行直接插入排序那是相当之快。
希尔排序思路
- 定义增量序列 Dk:Dm > Dm-₁ >…>D₁ = 1。
- 刚才的例子中:m 是选择增量的次数,D₃ = 5,D₂ = 3,D₁ = 1(第一次的增量为 5,第二次为 3 …)。
- 对每个 Dk 进行 Dk- 间隔,插入排序(k = M,M-1,…1)。
- 增量选择 5 的时候就进行 5 间隔插入排序,其余同理。
- 增量为 1 的时候,进行的是所有元素的直接插入排序。
希尔排序特点
- 一次移动,移动位置较大,跳跃式的接近排序后的最终位置。
- 最后一次只需要少量移动。
- 增量序列必须是递减的,最后一次必须是 1 间隔。
- 增量序列应该是互为质数的。
希尔排序算法
主程序
//按增量序列dlta[0...t-1]对顺序表L作希尔排序
void ShellSort(SqList &L,int dlta[],int t)//dk值依次存在dlta[t]中
{
for(k=0;k<t;k++)//规定有t趟希尔排序
{
ShelInsert(L,dlta[k]);//一趟增量为dlta[k]的插入排序
}
}//ShellSort
其中某一趟的排序操作
//对顺序表L做一趟增量是dk的希尔插入排序
void ShellInsert(SqList &L,int dk)
{
for(i=dk+1;i<=L.length;i++)
{
if(L.r[i].ley < L.r[i-dk].key) //需要将L.r[i]插入有序增量子表,
//将当前位置的元素和当前位置 - 间隔的位置的元素进行比较,
//如5间隔:假设当前位置为6,则需要和6-5=1号位置元素进行比较
{
L.r[0] = L.r[i]; //暂时存在L.r[0]
for(j = i-dk;j > 0&& L.r[0].key < L.r[j].key;j -= dk)
{
L.r[j+dk] = L.r[j]; //记录后移,直接找到插入位置
}
L.r[j+dk] = L.r[0]; //将r[0]即原r[i],插入到最终位置。
}
}
}
希尔排序算法分析
希尔排序的时间效率
希尔排序算法效率与增量序列的取值有关
- Hibbard 增量序列
- Dk = 2k-1 —— 相邻元素互为质数。
- 最坏情况:Tworst = O(n3/2)。
- 猜想:Tavg = O(n5/4)。
- Sedgewick 增量序列
- {1,5,19,41,109…}
- —— 9 X 4i - 9 X 2i +1 或者 4i - 3 X 2i +1
- 猜想:Tavg = O(n7/6) ,Tworst = O(n4/3)。
- {1,5,19,41,109…}
希尔排序算算的稳定性
希尔排序是一种不稳定的排序算法
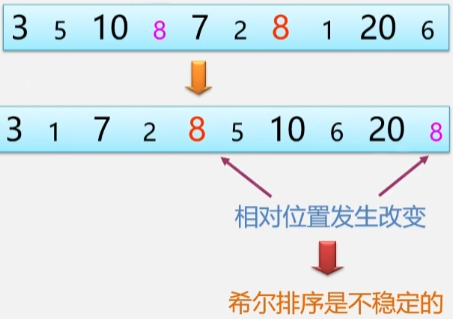
【例如】:现有这样一组数据,对它进行增量为 2(d=2) 的希尔排序。
- 每一组都包括一个字体大的元素,和一个字体小的。
- 排序完成之后发现,两个相同的元素 8 的相对位置变了
希尔排序算法分析
- 时间复杂度是 n 和 d 的函数:O(n1.25) ~ O(1.6n1.25) — 经验公式。
- 空间复杂度为 O(1)。
- 是一种不稳定的排序方法。
- 如何选择最佳的增量(d) 序列,目前尚未解决。
- 最后一个增量值必须为 1,无除了 1 之外的公因子。
- 不宜在链式存储结构上实现。
- 如何选择最佳的增量(d) 序列,目前尚未解决。