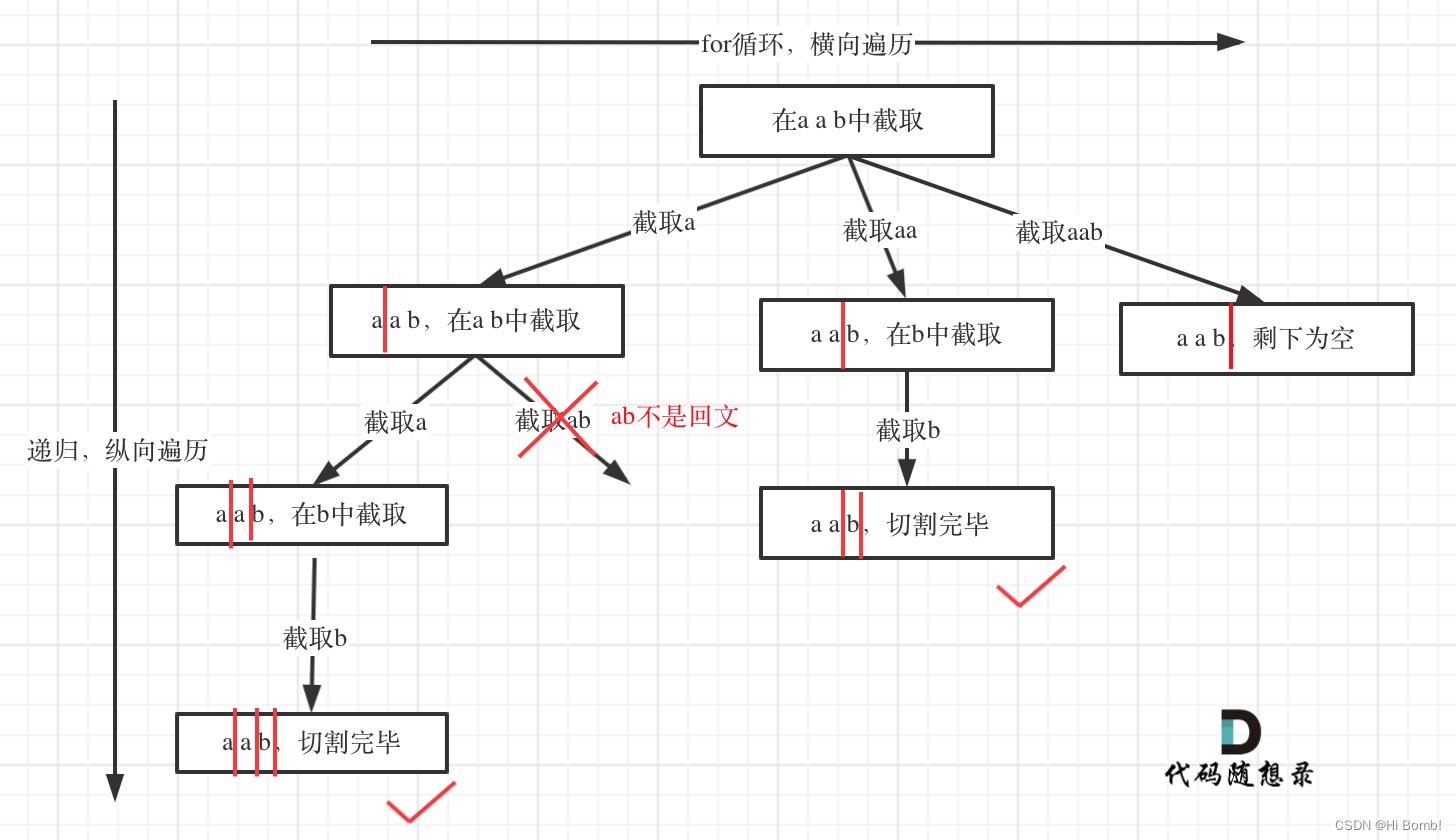
文章目录
- opencv函数cv2.warpAffine 和 cv2.warpPerspective 的理解和复现
- 1. warpAffine 函数处理仿射变换
- 2. warp_perspective
- 3, 实验
opencv函数cv2.warpAffine 和 cv2.warpPerspective 的理解和复现
1. warpAffine 函数处理仿射变换
仿射矩阵是2 * 3的矩阵。
首先进行坐标转换,然后应用插值
具体代码如下, 与opencv一致:
def warp_affine_forward(image, rot_mat, dst_h, dst_w):
M = rot_mat.reshape([2, 3])
hs, ws, cs = image.shape
hh, ww = np.arange(hs), np.arange(ws)
xx, yy = np.meshgrid(ww, hh)
sx, sy = xx, yy # 不缩放图像
tx, ty = M[0, 0] * sx + M[0, 1] * sy + M[0, 2], M[1, 0] * sx + M[1, 1] * sy + M[1, 2]
# tx = np.sum(M[0, :].reshape([1, 1, 3]) * np.dstack((sx, sy, np.ones_like(sx))), axis=-1)
# ty = np.sum(M[1, :].reshape([1, 1, 3]) * np.dstack((sx, sy, np.ones_like(sx))), axis=-1)
dhh, dww = np.arange(dst_h), np.arange(dst_w)
dxx, dyy = np.meshgrid(dww, dhh)
grid_x, grid_y = dxx, dyy
points = np.dstack((tx, ty))
# print(points.shape, image.shape, grid_x.shape)
out = griddata(points.reshape(-1, 2), image.reshape(-1, 3), (grid_x, grid_y), method='linear')
out[np.isnan(out)] = 0
return out
逆变换代码:
def warp_affine(image, rot_mat, dst_h, dst_w):
M = rot_mat.reshape([2, 3])
hs, ws, cs = image.shape
hh, ww = np.arange(dst_h), np.arange(dst_w)
xx, yy = np.meshgrid(ww, hh)
sx, sy = (xx + 0.5) * (ws / ws) - 0.5, (yy + 0.5) * (hs / hs) - 0.5 # 不缩放图像。
# sx, sy = (xx + 0.5) * (ws / dst_w) - 0.5, (yy + 0.5) * (hs / dst_h) - 0.5 # 缩放图像
tx, ty = M[0, 0] * sx + M[0, 1] * sy + M[0, 2], M[1, 0] * sx + M[1, 1] * sy + M[1, 2]
# tx = np.sum(M[0, :].reshape([1, 1, 3]) * np.dstack((sx, sy, np.ones_like(sx))), axis=-1)
# ty = np.sum(M[1, :].reshape([1, 1, 3]) * np.dstack((sx, sy, np.ones_like(sx))), axis=-1)
mask = ((tx < 0) + (ty < 0) + (tx > ws - 1) + (ty > hs - 1)) > 0
# print(mask.shape, mask.dtype, np.sum(mask))
out = interp_linear(image, tx, ty)
out[mask] = 0
return out
也可以求解转换矩阵的逆后,再正变换,结果相同。
其中用到重查找函数:根据tx,ty坐标位置,获取值
和cv2.remap函数相同。
def interp_linear(image, tx, ty):
'''
类似 cv2.remap 函数
:param image: h,w,c image np.float
:param tx: dst_h * dst_w, float , 目标位置x方向
:param ty: dst_h * dst_w, float , 目标位置y方向
:return:
'''
h, w, c = image.shape
hv, wv = ty, tx
hh = np.floor(hv).astype(np.int32)
ww = np.floor(wv).astype(np.int32)
u = hv - hh
v = wv - ww
# special case
u[hh < 0] = 0
hh[hh < 0] = 0
u[hh >= h - 1] = 1.0
hh[hh >= h - 1] = h - 2
v[ww < 0] = 0
ww[ww < 0] = 0
v[ww >= w - 1] = 1.0
ww[ww >= w - 1] = w - 2
# v = v.reshape(-1)
w00 = (1-u)*(1-v)
w01 = u * (1-v)
w10 = (1-u) * v
w11 = u*v
out = w00[..., None] * image[hh, ww] + w10[..., None] * image[hh, ww + 1] + w01[..., None] * image[(hh + 1), ww] + w11[..., None] * image[hh + 1, ww + 1]
return out
2. warp_perspective
warpPerspective 和 warpAffine 是类似的。
但是warpPerspective的转换矩阵是3*3的透视变换矩阵,经过变换后平行线可能不在平行
一个逆变换 和 两个正变换的代码如下:
# 逆变换函数
def warp_perspective(image, pers_mat, dst_h, dst_w):
M = pers_mat.reshape([3, 3])
hs, ws, cs = image.shape
hh, ww = np.arange(dst_h), np.arange(dst_w)
xx, yy = np.meshgrid(ww, hh)
sx, sy = (xx + 0.5) * (ws / ws) - 0.5, (yy + 0.5)* (hs / hs) - 0.5
# sx, sy = (xx + 0.5) * (ws / dst_w) - 0.5, (yy + 0.5) * (hs / dst_h) - 0.5 # 缩放图像
t = M[2, 0] * sx + M[2, 1] * sy + M[2, 2]
tx, ty = M[0, 0] * sx + M[0, 1] * sy + M[0, 2] , M[1, 0] * sx + M[1, 1] * sy + M[1, 2]
tx, ty = tx / t, ty / t
# out = np.zeros_like(image)
mask = ((tx < 0 ) + (ty < 0) + (tx > ws - 1) + (ty > hs - 1)) > 0
print(mask.shape, mask.dtype, np.sum(mask))
# out = interp_linear(image, tx, ty)
out = cv2.remap(image, tx.astype(np.float32), ty.astype(np.float32), interpolation=cv2.INTER_LINEAR)
out[mask] = 0
return out
# 正变化函数
def warp_perspective_forward(image, pers_mat, dst_h, dst_w):
M = pers_mat.reshape([3, 3])
hs, ws, cs = image.shape
hh, ww = np.arange(hs), np.arange(ws)
xx, yy = np.meshgrid(ww, hh)
sx, sy = xx, yy # 不缩放图像
t = M[2, 0] * sx + M[2, 1] * sy + M[2, 2]
tx, ty = M[0, 0] * sx + M[0, 1] * sy + M[0, 2] , M[1, 0] * sx + M[1, 1] * sy + M[1, 2]
tx, ty = tx / t, ty / t
# interp
dhh, dww = np.arange(dst_h), np.arange(dst_w)
dxx, dyy = np.meshgrid(dww, dhh)
grid_x, grid_y = dxx, dyy
points = np.dstack((tx, ty))
# print(points.shape, image.shape, grid_x.shape)
out = griddata(points.reshape(-1, 2), image.reshape(-1, 3), (grid_x, grid_y), method='linear')
out[np.isnan(out)] = 0
return out
# 正变换函数:这里利用np.linalg.inv 求逆矩阵,然后按照warp_perspective的方式进行
def warp_perspective_forward2(image, pers_mat, dst_h, dst_w):
M = pers_mat.reshape([3, 3])
M_inv = np.linalg.inv(M)
M = M_inv
hs, ws, cs = image.shape
hh, ww = np.arange(dst_h), np.arange(dst_w)
xx, yy = np.meshgrid(ww, hh)
sx, sy = (xx + 0.5) * (ws / ws) - 0.5, (yy + 0.5) * (hs / hs) - 0.5
# sx, sy = (xx + 0.5) * (ws / dst_w) - 0.5, (yy + 0.5) * (hs / dst_h) - 0.5 # 缩放图像
t = M[2, 0] * sx + M[2, 1] * sy + M[2, 2]
tx, ty = M[0, 0] * sx + M[0, 1] * sy + M[0, 2], M[1, 0] * sx + M[1, 1] * sy + M[1, 2]
tx, ty = tx / t, ty / t
# out = np.zeros_like(image)
mask = ((tx < 0) + (ty < 0) + (tx > ws - 1) + (ty > hs - 1)) > 0
print(mask.shape, mask.dtype, np.sum(mask))
# out = interp_linear(image, tx, ty)
out = cv2.remap(image, tx.astype(np.float32), ty.astype(np.float32), interpolation=cv2.INTER_LINEAR)
out[mask] = 0
return out
3, 实验
验证以上代码和opencv中的一致性
import cv2
import numpy as np
from matplotlib import pyplot as plt
from scipy.interpolate import griddata
def cal_sobel(img):
#分别求X,Y方向的梯度
grad_X=cv2.Sobel(img,-1,1,0)
grad_Y=cv2.Sobel(img,-1,0,1)
#求梯度图像
grad=cv2.addWeighted(grad_X,0.5,grad_Y,0.5,0)
return grad
if __name__ == "__main__":
file1 = r'test.jpg'
image1 = cv2.imread(file1) / 255
image1 = cv2.resize(image1, (0, 0), fx=0.5, fy=0.5)
h, w, c = image1.shape
print(h, w, c)
center = (w // 2, h // 2)
angle = -50
scale = 0.6
rot_mat = cv2.getRotationMatrix2D(center, angle, scale)
print(rot_mat)
dst_h, dst_w = int(image1.shape[0] * 0.7), int(image1.shape[1]* 0.7)
image2 = cv2.warpAffine(image1, rot_mat, (dst_w, dst_h))
center = (w // 2, h // 2)
angle = 50
scale = 1 / 0.6
rot_mat2 = cv2.getRotationMatrix2D(center, angle, scale)
print(rot_mat2)
image3 = warp_affine(image1, rot_mat2, dst_h, dst_w)
image4 = warp_affine_forward(image1, rot_mat, dst_h, dst_w)
plt.figure()
plt.subplot(221)
plt.imshow(image1)
plt.subplot(222)
plt.imshow(image2)
plt.subplot(223)
plt.imshow(image3)
plt.subplot(224)
plt.imshow(image4)
plt.show()
# 根据4个点求透视转换
pts1 = np.float32([[56, 65], [368, 52], [28, 387], [389, 390]])
pts2 = np.float32([[0, 0], [300, 0], [0, 300], [300, 300]])
M = cv2.getPerspectiveTransform(pts1, pts2)
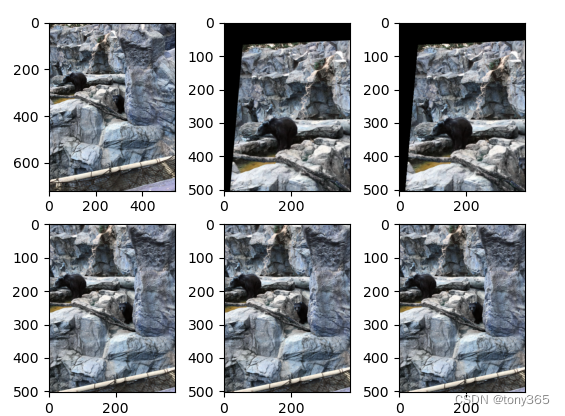
image2 = cv2.warpPerspective(image1, M, (dst_w, dst_h), flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP)
image3 = warp_perspective(image1, M, dst_h, dst_w)
image4 = cv2.warpPerspective(image1, M, (dst_w, dst_h), flags=cv2.INTER_LINEAR)
image5 = warp_perspective_forward(image1, M, dst_h, dst_w)
image6 = warp_perspective_forward2(image1, M, dst_h, dst_w)
plt.figure()
plt.subplot(231)
plt.imshow(image1)
plt.subplot(232)
plt.imshow(image2)
plt.subplot(233)
plt.imshow(image3)
plt.subplot(234)
plt.imshow(image4)
plt.subplot(235)
plt.imshow(image5)
plt.subplot(236)
plt.imshow(image6)
plt.show()
运行上面的代码,实验结果如下:
warp affine实验结果:
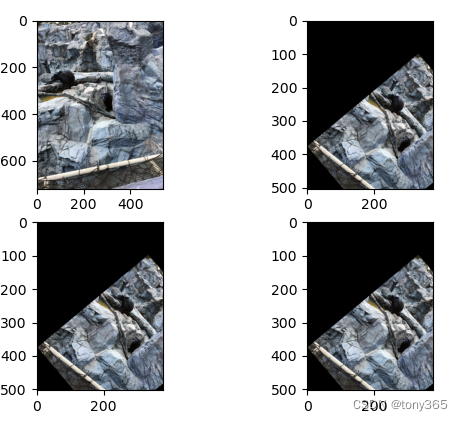
warp perspective 实验结果