文章目录
- 一:什么是欠拟合和过拟合
- 二:正则化技术
- (1)加入正则项
- ①:L1正则项
- ②:L2正则项
- (2)Dropout(暂退法)
我们训练模型的目的是为了让模型真正发现一种泛化模式,而不是说只是简简单单的记住了训练数据,只有这样,模型在遇到全新的数据时,也能成功预测
一:什么是欠拟合和过拟合
欠拟合(underfitting):训练误差和验证误差都很严重,他们之间仅有一点差距。这意味着,模型可能过于简单,也即表达能力差
过拟合(overfitting)(最为常见):模型的训练误差要明显低于验证误差。当然注意,即便是最好的预测模型,它在训练数据上的表现往往⽐在验证数据上好得多。最终,我们通常更关⼼验证误差,⽽不是训练误差和验证误差之间的差距
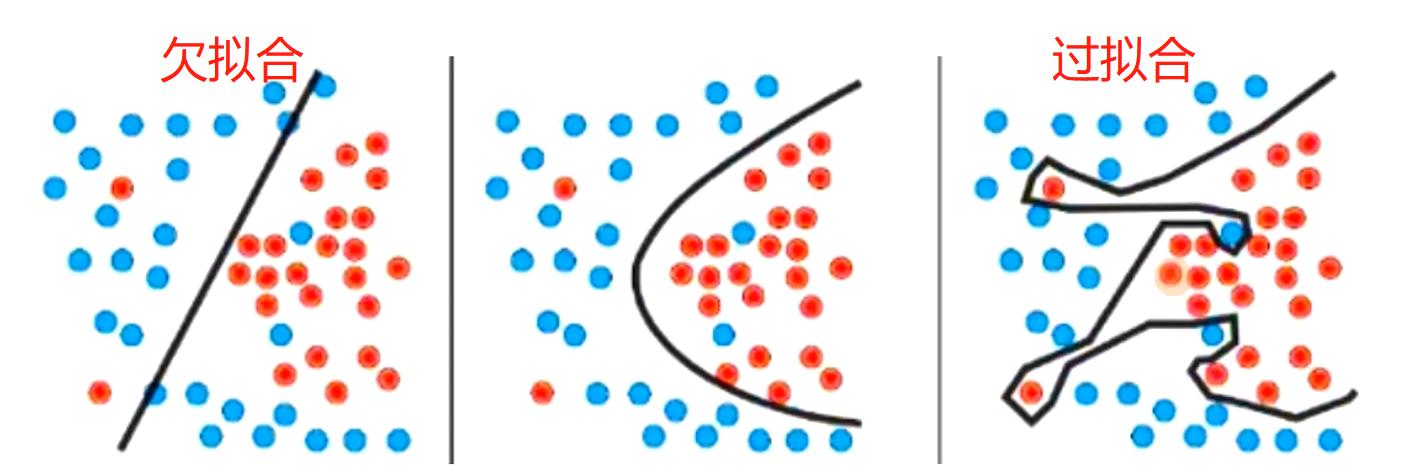
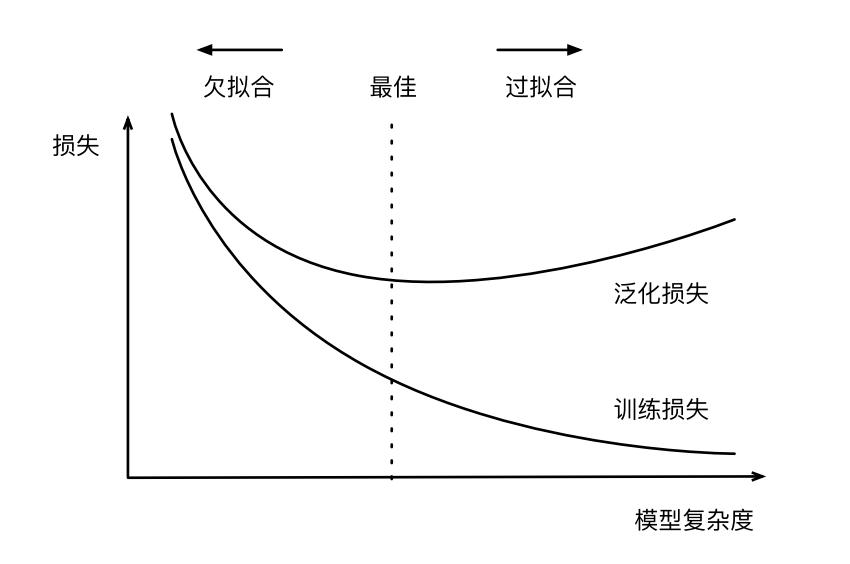
前面也说过,在进行模型选择时,不能一味地认为训练误差越小的模型越好,因为此时可能已经到达过拟合状态,此时它在测试数据上误差反而会变大,所以要选择损失函数刚刚收敛时的模型作为最佳模型
二:正则化技术
正则化:正则化旨在减少泛化误差而不是训练误差,也就是说,正则化的目的是为了防止模型过拟合,降低泛化误差,从而提高泛化能力
正则化技术在深度学习中主要用于了抑制过拟合,主要有四种
- 加正则项(惩罚项):使用最为广泛,通常只对权重做惩罚而不对偏置做正则惩罚,最常用的是L1和L2
- Dropout(暂退法)
- 数据增广
- 早停法:配合日志
(1)加入正则项
①:L1正则项
L1正则项 在原损失函数后面加入L1范数(非零元素的绝对值之和)
J
︿
(
ω
;
X
,
y
)
=
J
(
ω
;
X
,
y
)
+
α
∣
∣
ω
∣
∣
1
\mathop{J}\limits^{︿}(\omega;X,y) = J(\omega;X, y) + \alpha||\omega||_{1}
J︿(ω;X,y)=J(ω;X,y)+α∣∣ω∣∣1
计算梯度后,
ω
\omega
ω的更新公式为
ω ← ω − ξ α s i g n ( ω ) − ξ ∇ ω J ( ω ; X , y ) \omega \leftarrow \omega - \xi\alpha sign(\omega)-\xi \nabla_{\omega}J(\omega;X,y) ω←ω−ξαsign(ω)−ξ∇ωJ(ω;X,y)
可以看出,L1正则化会使得 @ w @w @w向0靠近,使网络中的权重尽可能为0,使网络中某些神经元失效,以此防止过拟合
- 当 ω > 0 \omega>0 ω>0时,梯度下降时更新后的 ω \omega ω变小
- 当 ω > < 0 \omega><0 ω><0时,梯度下降时更新后的 ω \omega ω变大
特点
- 特征选择器
- 模型稀疏性
②:L2正则项
L2正则项: 在原损失函数后面加入L2范数(向量元素的平方和再开平方)
J
︿
(
ω
;
X
,
y
)
=
J
(
ω
;
X
,
y
)
+
α
2
ω
T
ω
\mathop{J}\limits^{︿}(\omega ;X,y) = J(\omega;X, y)+\frac{\alpha}{2}\omega^{T}\omega
J︿(ω;X,y)=J(ω;X,y)+2αωTω
**计算梯度后,
ω
\omega
ω的更新公式为
ω ← ( 1 − ξ α ) ω − ξ ∇ ω J ( ω ; X , y ) \omega \leftarrow (1-\xi\alpha)\omega - \xi \nabla_{\omega}J(\omega;X, y) ω←(1−ξα)ω−ξ∇ωJ(ω;X,y)
可以看到,在每次执行梯度更新前,先会收缩权重向量(权重衰减),因此L2正则化可以让权重变得更小
特点
- 连续可导
- 易于训练
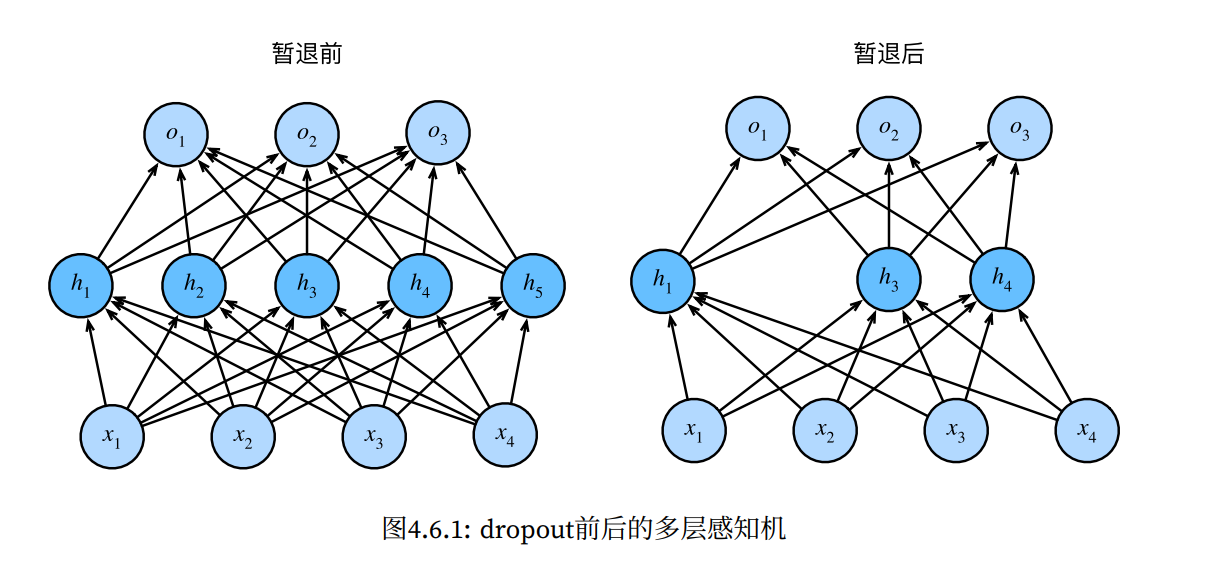
(2)Dropout(暂退法)
Dropout(暂退法):对于Dropout算法,在模型训练时,它会以下概率丢弃神经元