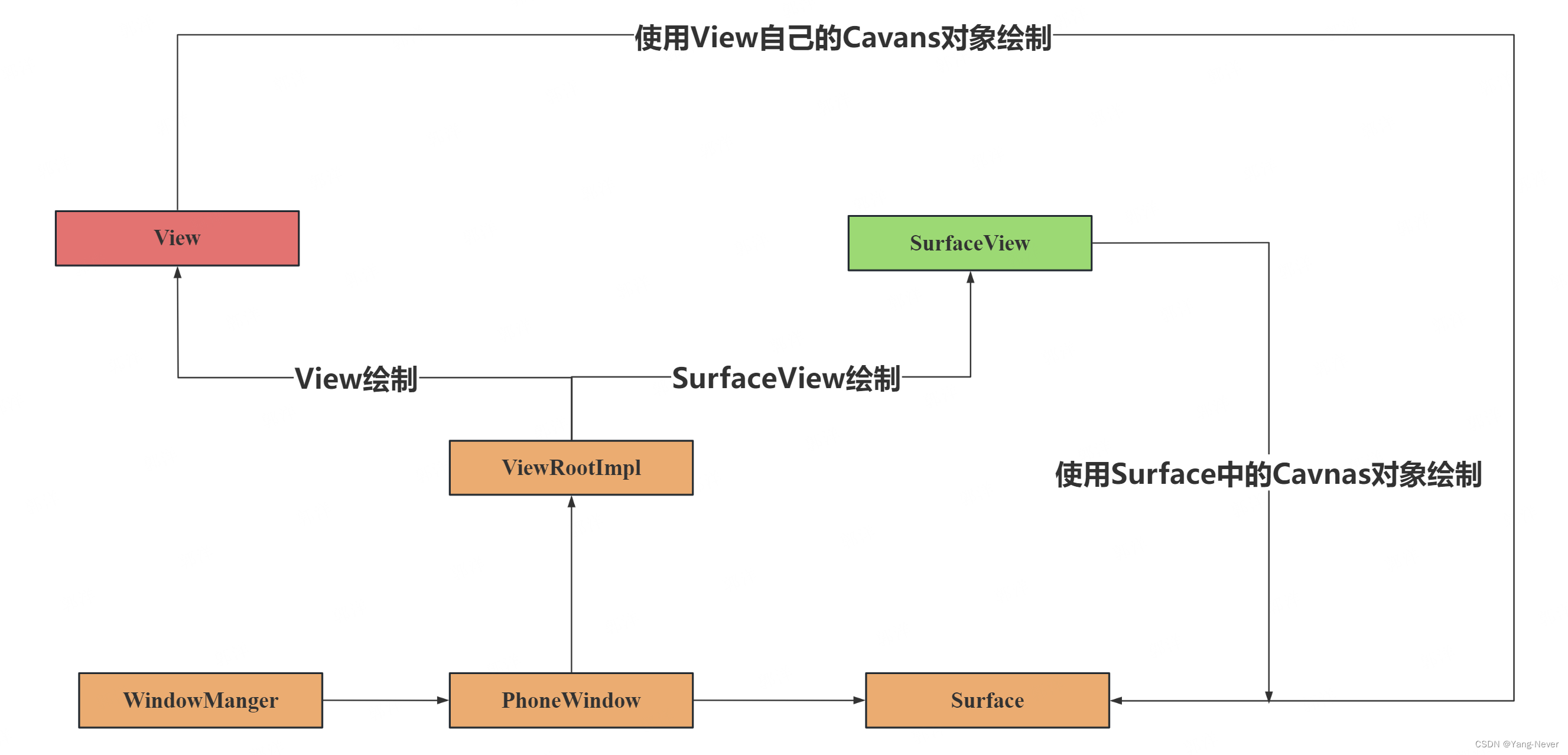
对数据的预处理:
(a)、调整数据的方差;
(b)、标准化:将数据标准化为具有零均值和单位方差;(均值方差归一化(Standardization))
(c)、最值归一化,也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 , 1]之间
(a)、调整数据的方差

均方差=标准差
方差的定义是:离平均值的平方距离的平均。
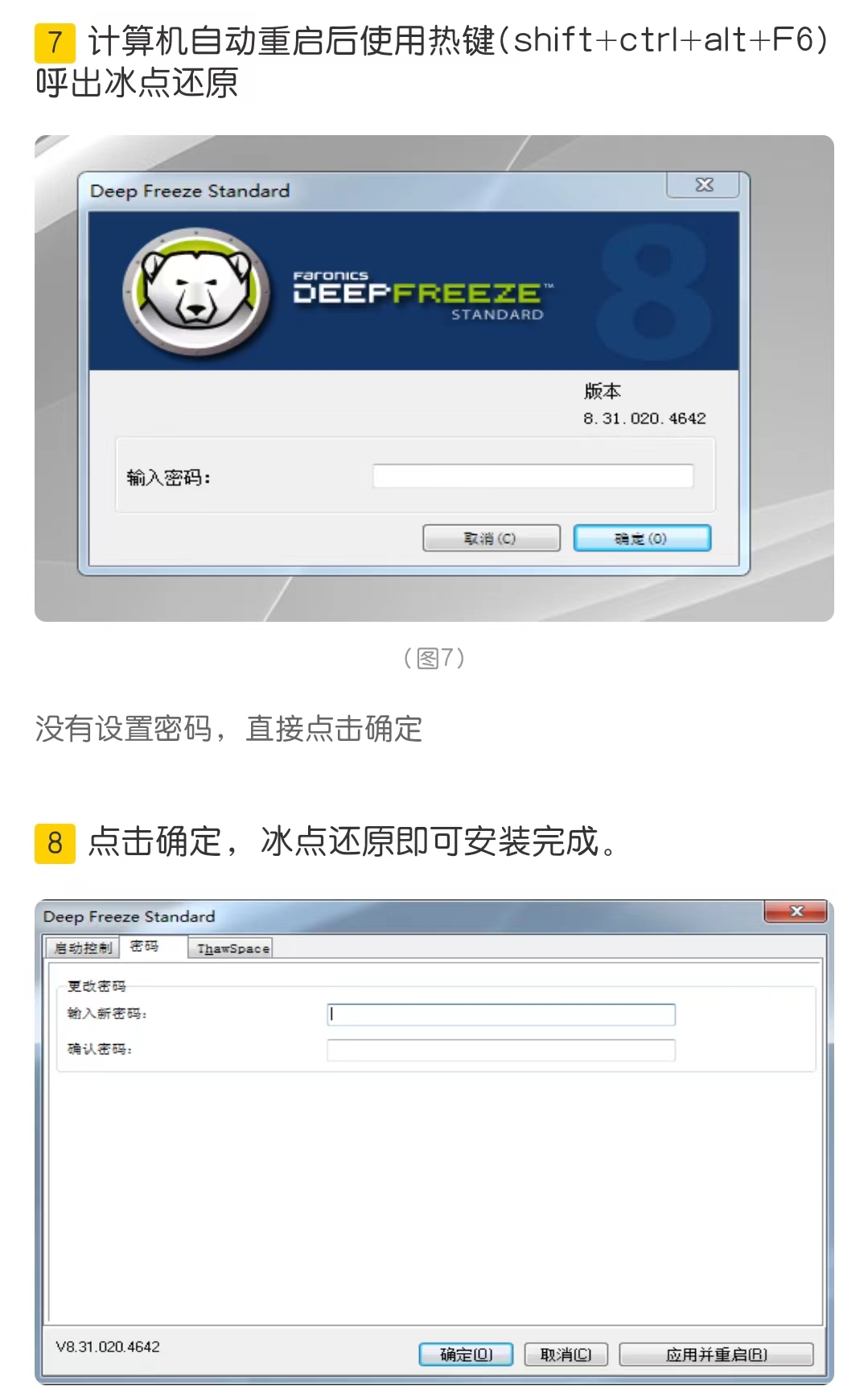
(b)、标准化
也称为均值归一化(mean normaliztion), 给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1。转化函数为:
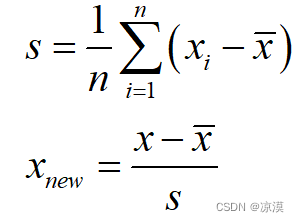
虽然该方法在无量纲化过程中利用了所有的数据信息,但是该方法在无量纲化后不仅使得转换后的各变量均值相同,且标准差也相同,即无量纲化的同时还消除了各变量在变异程度上的差异,从而转换后的各变量在聚类分析中的重要性程度是同等看待的。
(c)、最值归一化
也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 , 1]之间。
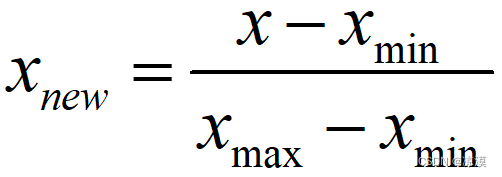
将一列数据变化到某个固定区间(范围)中,通常,这个区间是[0, 1] 或者(-1,1)之间的小数。主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速。
注意:由于极值化方法在对变量无量纲化过程中仅仅与该变量的最大值和最小值这两个极端值有关,而与其他取值无关,这使得该方法在改变各变量权重时过分依赖两个极端取值。
所用语言---matlab,python
matlab
%% 调整数据范围 预处理 调整方差到0.02
K=sqrt(0.02/var(inputData));
inputData = inputData*K;
K=sqrt(0.02/var(targetData));
targetData = targetData*K;%% 标准化
mu = mean(inputData);
sig = std(inputData); %标准差std函数
inputData = (inputData - mu) / sig;
mu = mean(targetData);
sig = std(targetData);
targetData = (targetData - mu) / sig;
% 预处理 归一化
inputData= mapminmax(inputData, 0, 1);
targetData= mapminmax(targetData, 0, 1);python
import numpy as np
inputData=x
targetData=y
K=np.sqrt(0.02/np.var(inputData))
inputData=np.dot(inputData, K)
K=np.sqrt(0.02/np.var(targetData))
targetData=np.dot(targetData, K)将数据标准化
import numpy as np
inputData=x
targetData=y
input_mean=np.mean(inputData)
input_std=np.std(inputData)
inputData=(inputData-input_mean)/input_std最值归一化适用于数据有明显边界的情况,例如考试成绩。该方法是将所有数据映射到[0,1]之间
(x-np.min(x))/(np.max(x)-np.min(x)) # 最值归一化