YOLO系列理论解读
YOLO v1(You Only Look Once:Unified, Real-Time Object Detection)
YOLO v1实现步骤
- 将一幅图像分成SxS个网格(grid cell),如果某个object的中心落在这个网格中,则这个网格就负责预测这个object。
通常情况下将S取值为S=7划分为7x7的一个区域。

2)每个网格要预测B个bounding box,每个bounding box除了要预测位置之外,还要附带预测一个confidence值。每个网格还要预测c个类别的分数。
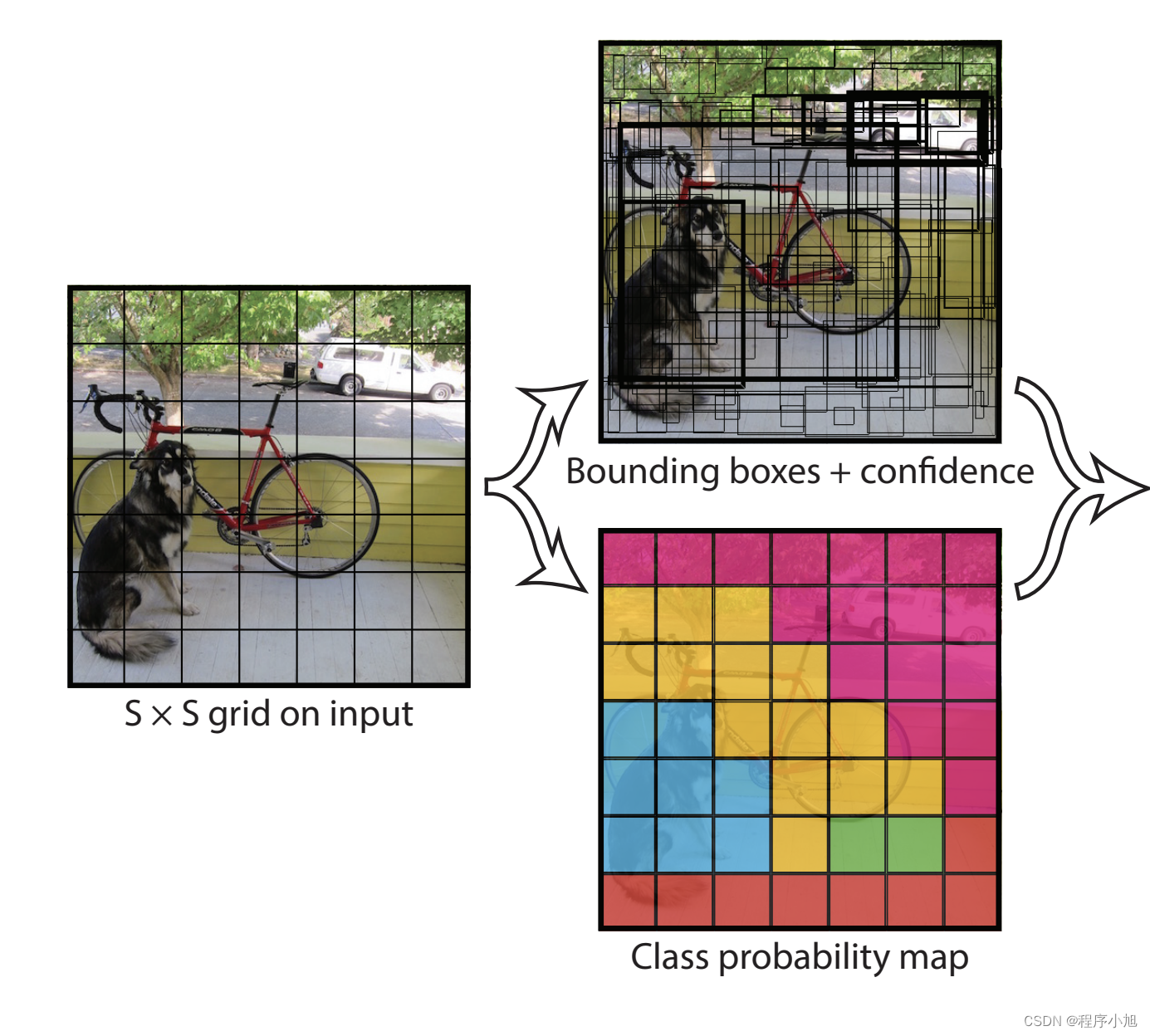
通常情况下的B=2使用PASCAL VOC进行训练类别数为20说明C=20

论文中提到了这么一段话。
For evaluating YOLO on PASCAL VOC, we use S = 7, B = 2. PASCAL VOC has 20 labelled classes so C = 20. Our final prediction is a 7 × 7 × 30 tensor.
说明了最后得到的预测参数的值是7x7x30个参数值,这和我们的网络结构之间有很大的关系。
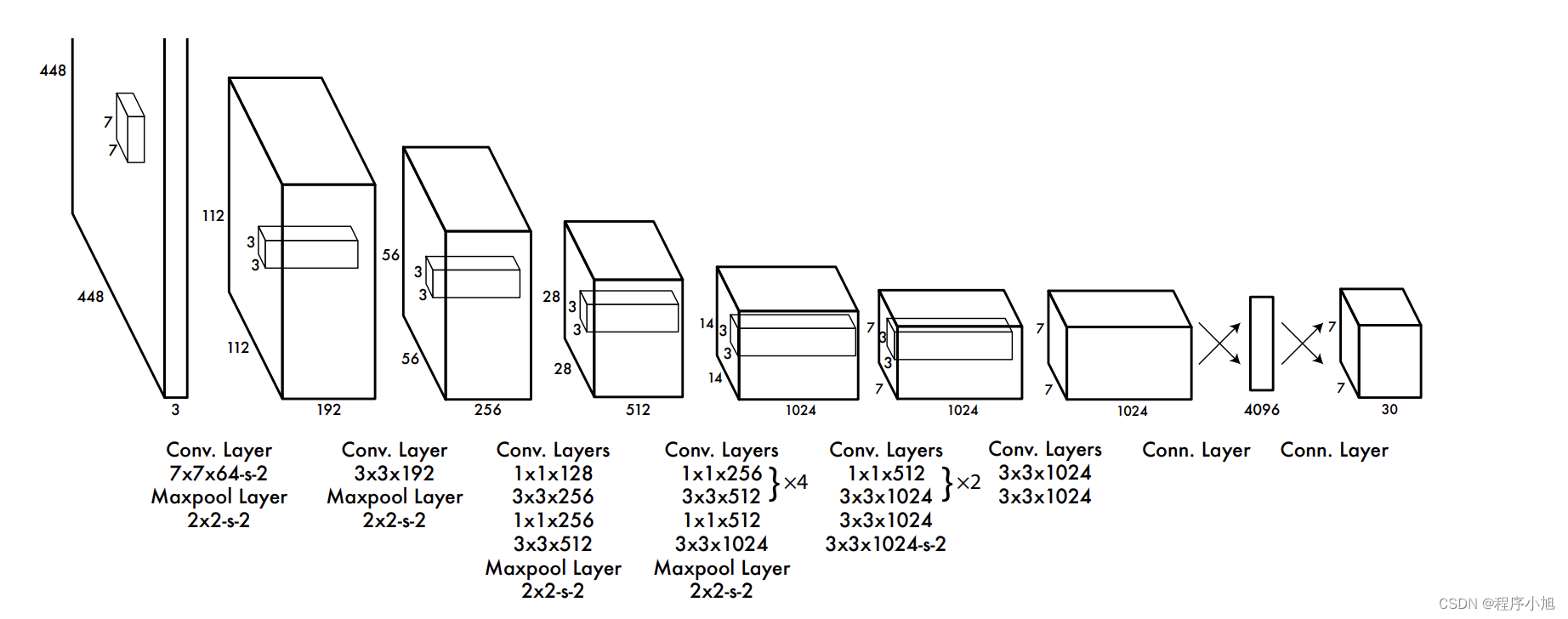
我们将输入的448x448像素的三通道图片,经过设计的网络之后可以得到的是7x7x30的输出特征图。
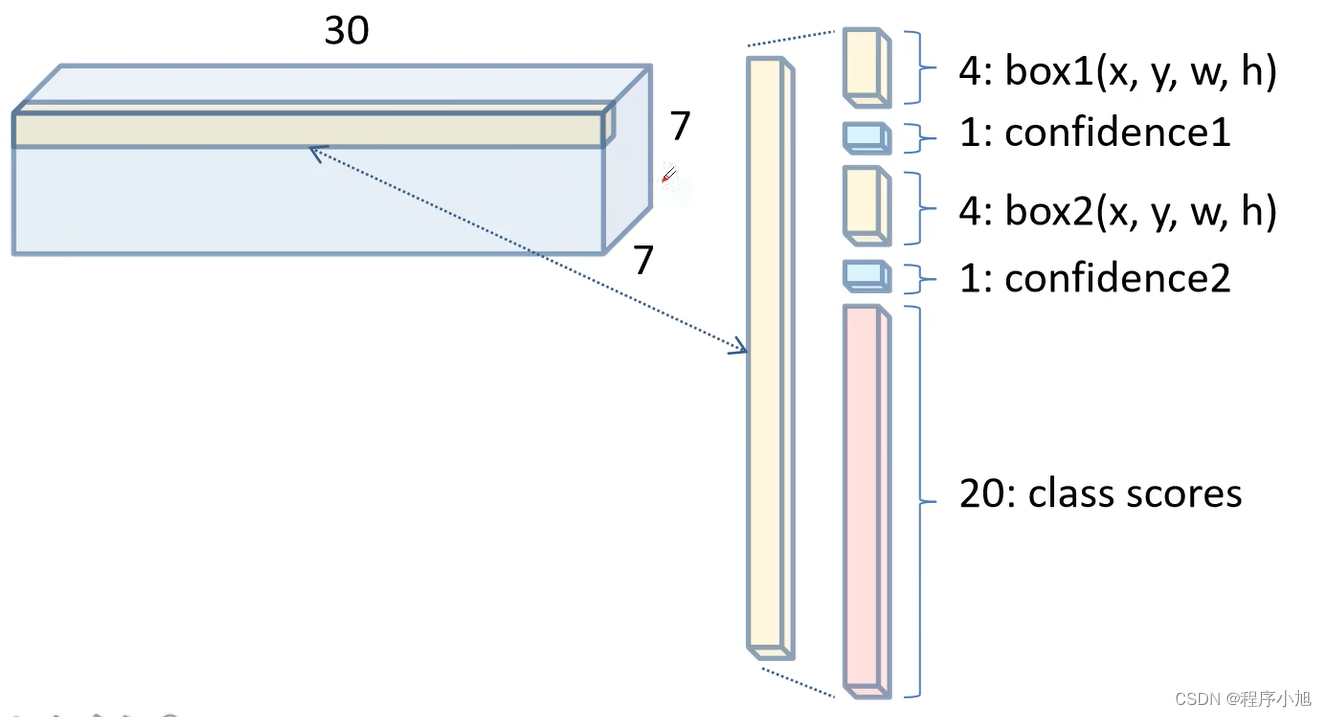
因为论文中提到了B=2一个网格会给出两个边界框的预测值,共7x7=49个划分之后的网格
每一个1x1 x30个通道的网格的参数分布为 边界框1的4个坐标位置中心位置x,y与高度和宽度,边界框1的confidence 边界框2的4个坐标位置中心位置x,y与高度和宽度,边界框2的confidence C=20的每一个类别的预测分数,用通道长度30来进行表示。

Each bounding box consists of 5 predictions: x, y, w, h,
and confidence. The (x, y) coordinates represent the center
of the box relative to the bounds of the grid cell. The width
and height are predicted relative to the whole image. Finally
the confidence prediction represents the IOU between the
predicted box and any ground truth box.
其中给出的X Y的值是相对于中心点的相对值,而w和h是相对与图像大小的相对值。

下面给出了confidence的一个计算过程,若网格框中没有物体存在,将其定义为0(pr值)若有物体存在pr值定义为1 最后confidence = IOU X PR
we define confidence as Pr(Object) ∗ IOUtruthpred . If noobject exists in that cell, the confidence scores should bezero. Otherwise we want the confidence score to equal theintersection over union (IOU) between the predicted box and the ground truth
最后给出每一个类别概率的计算公式是怎样得到的:

再一次给出Yolo v1论文中的网络结构图。其中包括了与4096个神经元进行全连接的操作,之后在进行一个Reshape处理得到30x30 x7的输出结构

损失函数
yolo v1的损失函数个人感觉是及其复杂的,在论文中给出的函数表达形式为:
λ coord ∑ i = 0 S 2 ∑ j = 0 B 1 i j obj [ ( x i − x ^ i ) 2 + ( y i − y ^ i ) 2 ] + λ coord ∑ i = 0 S 2 ∑ j = 0 B 1 i j obj [ ( w i − w ^ i ) 2 + ( h i − h ^ i ) 2 ] + ∑ i = 0 S 2 ∑ j = 0 B 1 i j obj ( C i − C ^ i ) 2 + λ noobj ∑ i = 0 S 2 ∑ j = 0 B 1 i j n o o b j ( C i − C ^ i ) 2 + ∑ i = 0 S 2 1 i obj ∑ c ∈ classes ( p i ( c ) − p ^ i ( c ) ) 2 \begin{array}{l} \lambda_{\text {coord }} \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {obj }}\left[\left(x_{i}-\hat{x}_{i}\right)^{2}+\left(y_{i}-\hat{y}_{i}\right)^{2}\right] \\ +\lambda_{\text {coord }} \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {obj }}\left[\left(\sqrt{w_{i}}-\sqrt{\hat{w}_{i}}\right)^{2}+\left(\sqrt{h_{i}}-\sqrt{\hat{h}_{i}}\right)^{2}\right] \\ +\sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {obj }}\left(C_{i}-\hat{C}_{i}\right)^{2} \\ +\lambda_{\text {noobj }} \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\mathrm{noobj}}\left(C_{i}-\hat{C}_{i}\right)^{2} \\ +\sum_{i=0}^{S^{2}} \mathbb{1}_{i}^{\text {obj }} \sum_{c \in \text { classes }}\left(p_{i}(c)-\hat{p}_{i}(c)\right)^{2} \end{array} λcoord ∑i=0S2∑j=0B1ijobj [(xi−x^i)2+(yi−y^i)2]+λcoord ∑i=0S2∑j=0B1ijobj [(wi−w^i)2+(hi−h^i)2]+∑i=0S2∑j=0B1ijobj (Ci−C^i)2+λnoobj ∑i=0S2∑j=0B1ijnoobj(Ci−C^i)2+∑i=0S21iobj ∑c∈ classes (pi(c)−p^i(c))2

整个公式损失的计算采用的是误差平方和的形式来进行实现的即:预测值减去真实的标签值,在取平方
符号含义的说明:
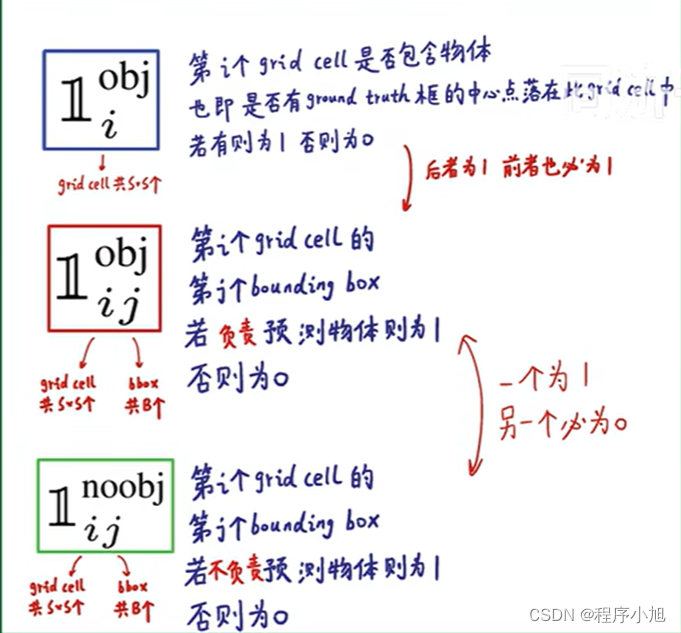
在之前的机器学习中该符号也有一定的应用。
对于损失函数的定义包括了以下的三个部分:边界框损失,confidence损失和最后的分类损失三部分损失共同构成
存在问题

Yolo v1对小的集群目标的预测效果差,例如之前论文值提到的对图片中的较小的鸟群有较差的预测效果。
YOLO V2 (YOLO9000)
因为yolo v2可以检测出9000个类别的物体,也称为yolo9000
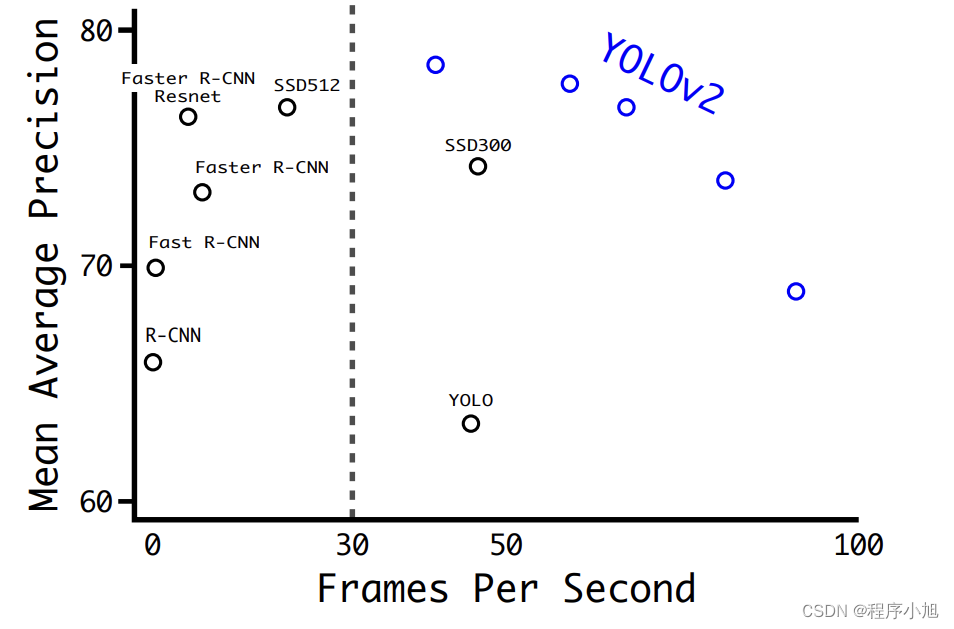
在当时的论文中可以看出yolov2的map值和计算速度都达到了当时最高的水准。
v2的改进
- Batch Normalization(引入了BN层)
提高了map值2%替代正则化的操作,同时也去除了dropout操作
Batch normalization leads to significant improvements in convergence while eliminating the need for other forms of regularization [7]. By adding batch normalization on all of the convolutional layers in YOLO we get more than 2% improvement in mAP. Batch normalization also helps regularize the model. With batch normalization we can remove dropout from the model without overfitting
- High Resolution Classifier(更高分辨率的分类器)
- Convolutional With Anchor Boxes.(使用锚框来进行预测)
增加了召回率
- Fine-Grained Features(结合更底层的特征信息)
将高层信息与相对低层的信息之间进行融合的操作。通过passthrough layer来进行实现的
passthrough layer将高层将13x13的结果与高层的特征图26x26x512进行一个结合的操作。
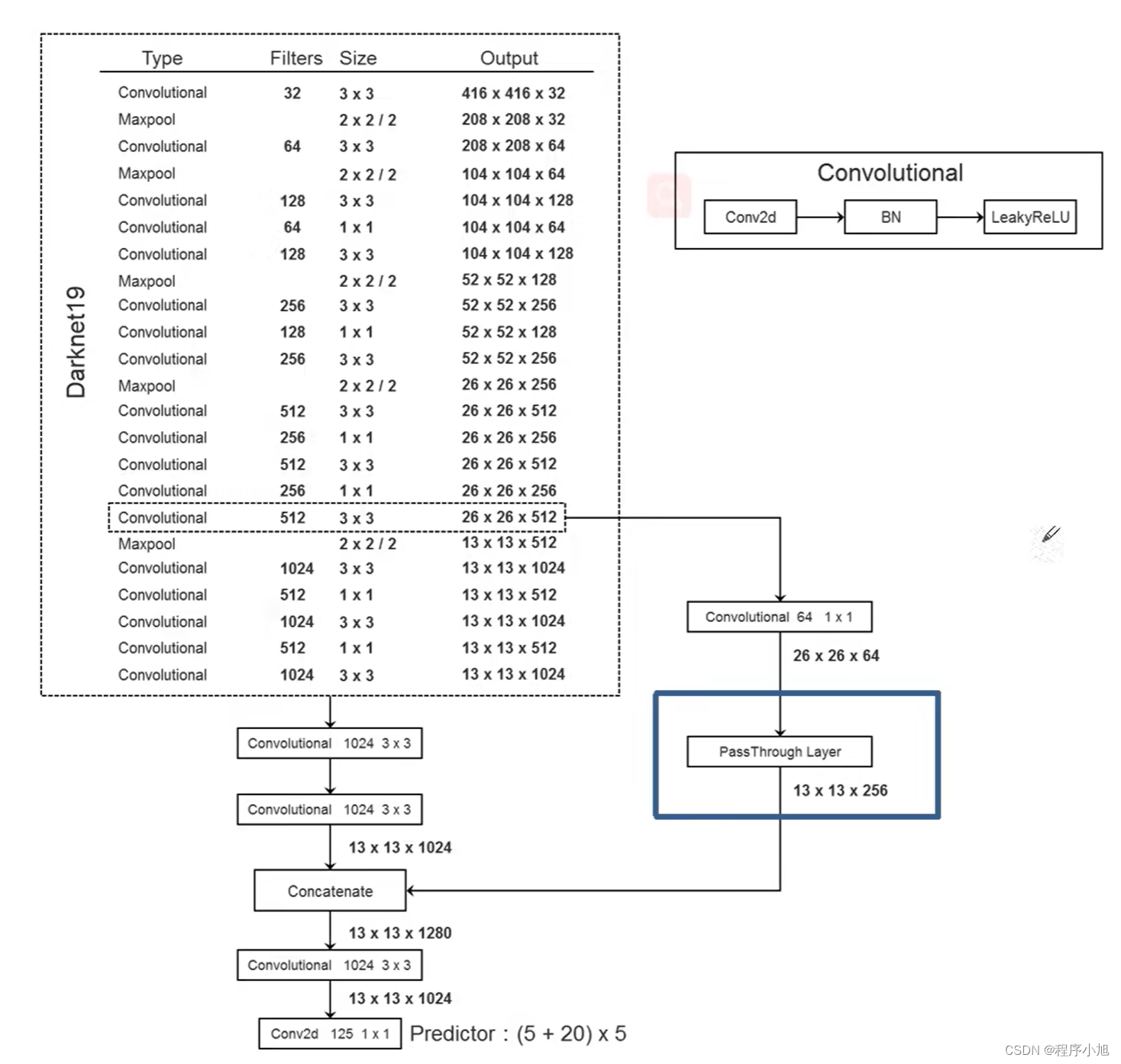
在通过PassThrough Layer (W/2, H/2, Cx4)时如图所示,高度和宽度会变为原来的一半,即26—13而通道数变为原来的4倍
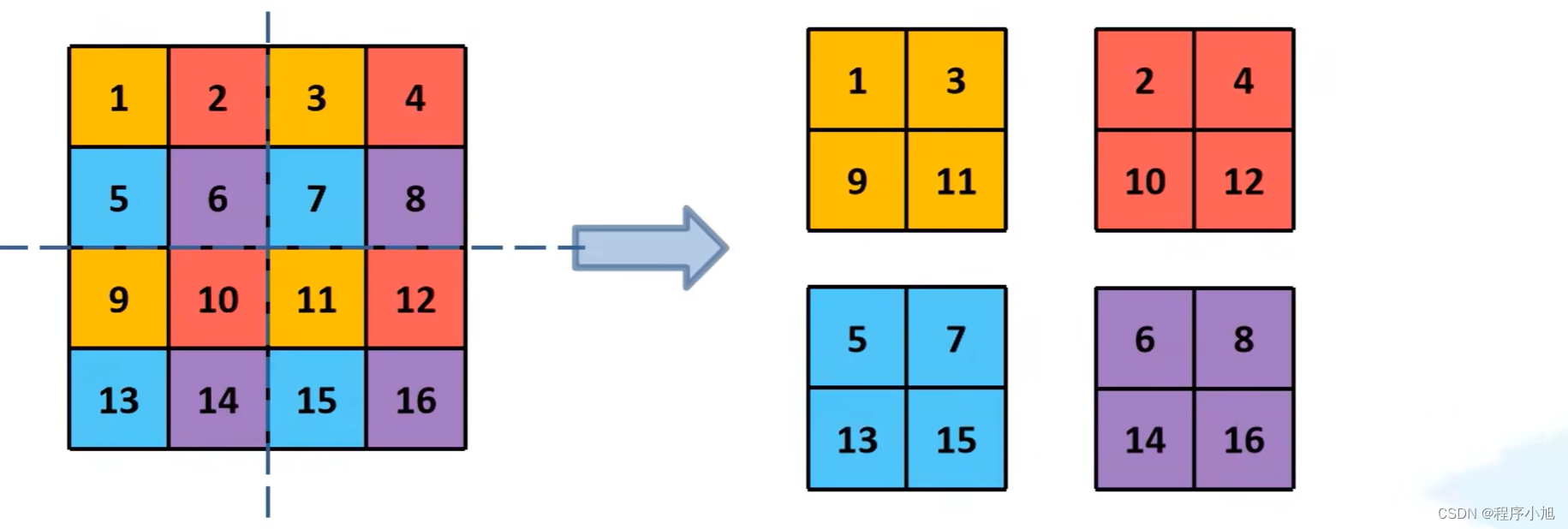
中间连接有一个1x1的卷积层来进行通道的压缩与降维操作。
- Multi-Scale Training(采用多尺度的训练方法)
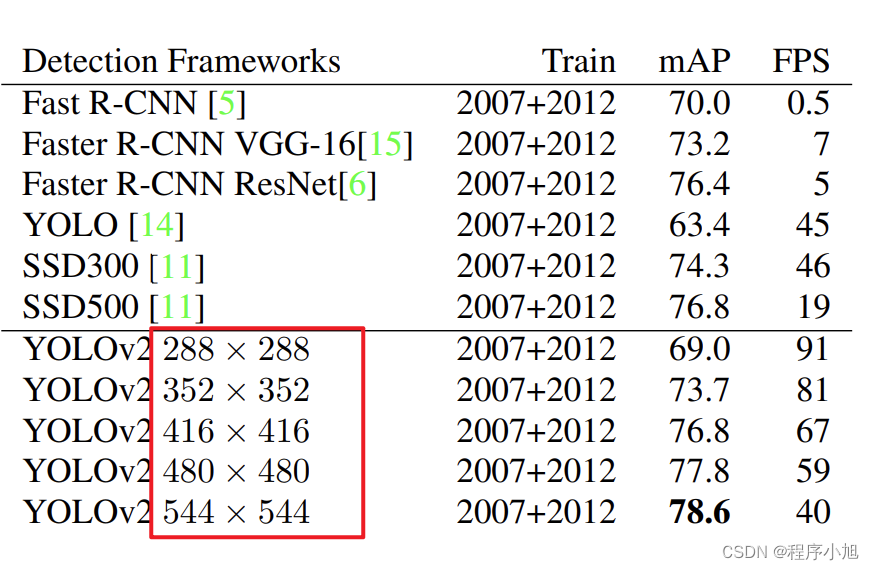
following multiples of 32: {320, 352, …, 608}. Thus the
smallest option is 320 × 320 and the largest is 608 × 608.
We resize the network to that dimension and continue training.
采用的全部的输入都是32的整数倍。
BackBone骨干网络
Yolo v2使用的网络架构为:Darknet-19作为其骨干网络(224x224的输入共19个卷积层)模型结构图。
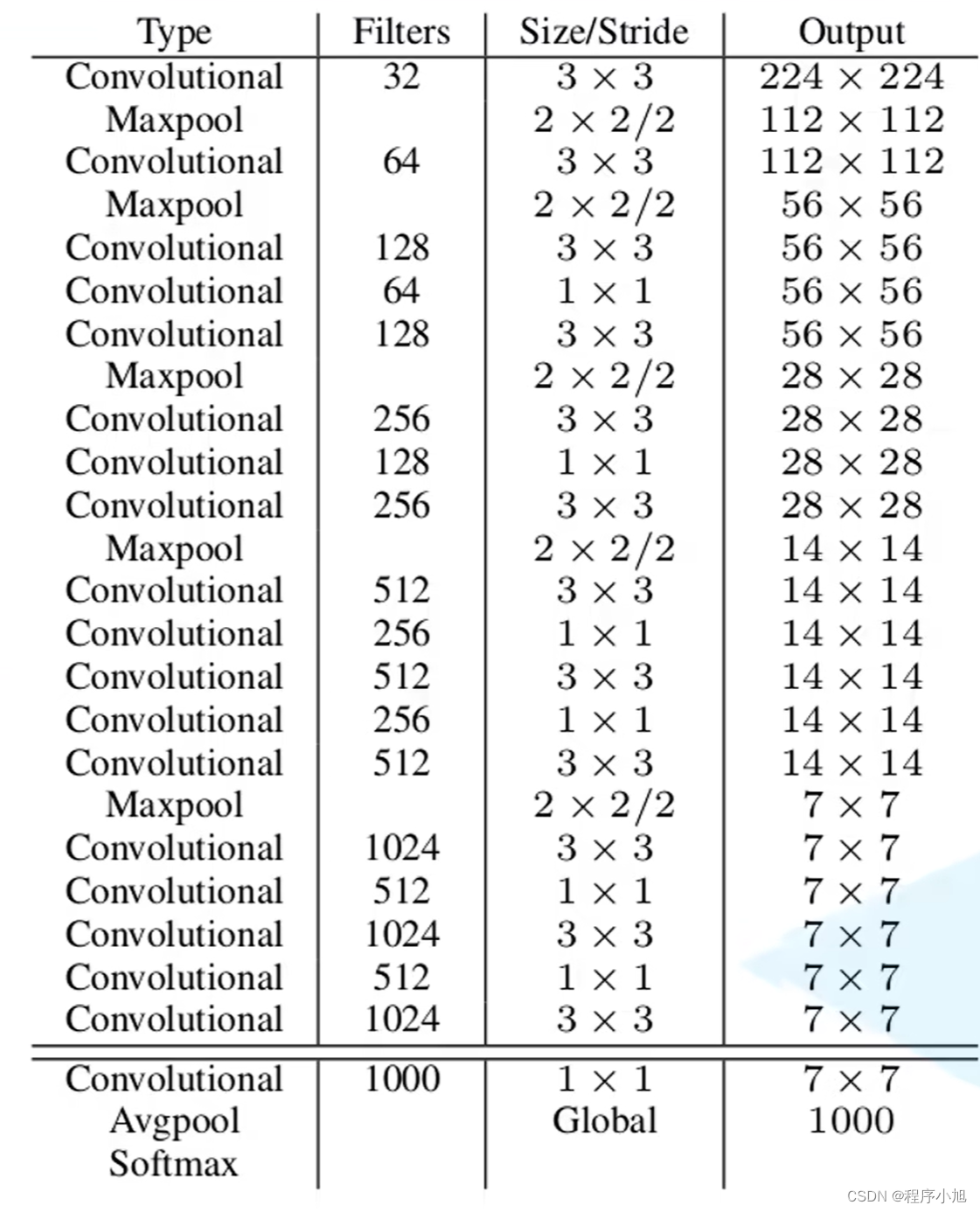
不同之处在于YOLO v2使用的输入是448x448或32整数倍的一个输入。
网络结构:
在去掉backbone的最后一层卷积层的基础上,我们添加了三个3x3卷积核大小为1024的三个卷积层。
最后在接一个1x1的卷积层,输出的个数即为我们要检测的物体的类别数量。
输出的125是20个类别 4个坐标 一个confidence 使用5个锚框最后在x5
125 =(20+5) x 5
YOLO V3( An Incremental Improvement)
主干网络
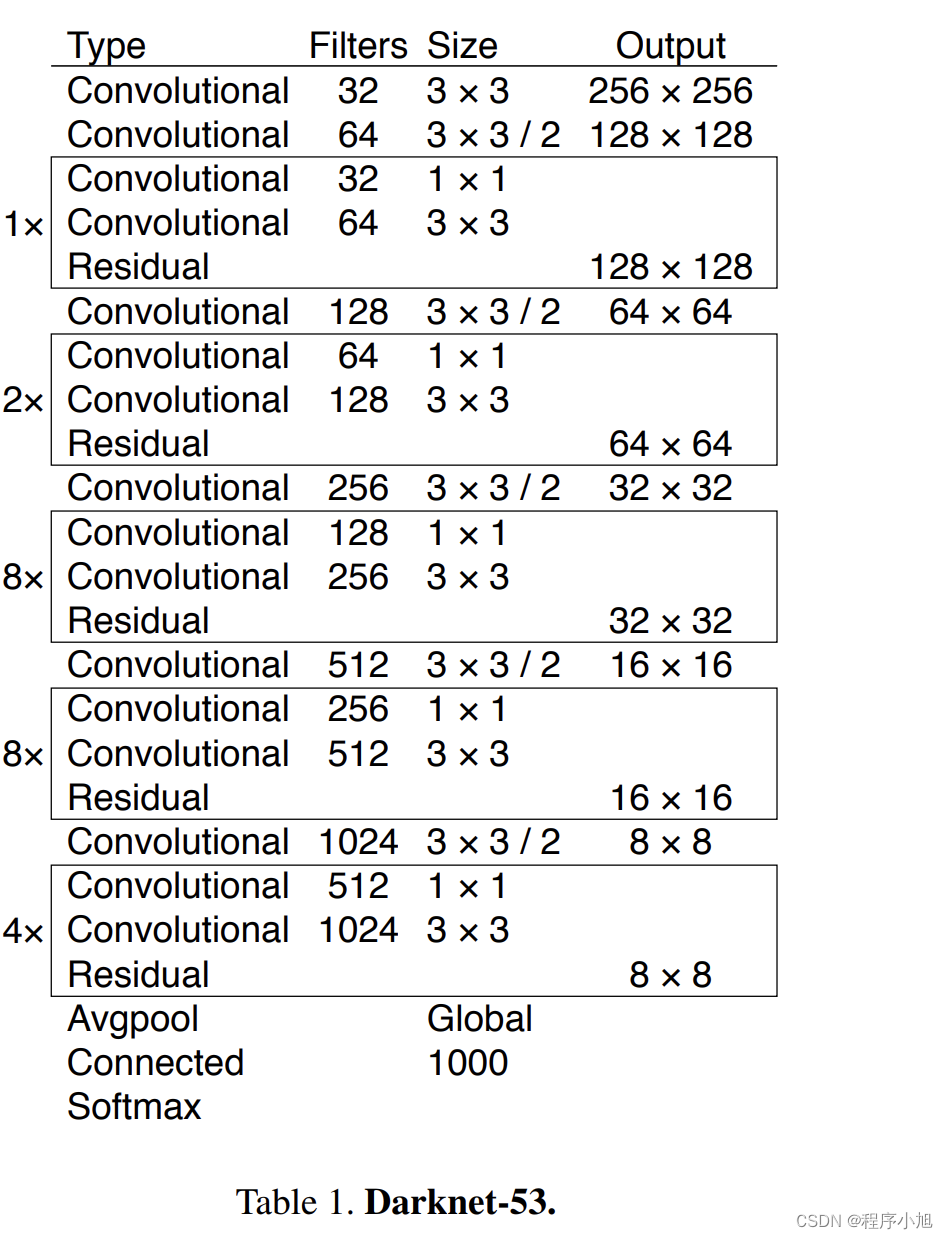
Darknet-53:53层网络的特点通过卷积层替换之前的下采样层,使得检测的效果得到了提升。
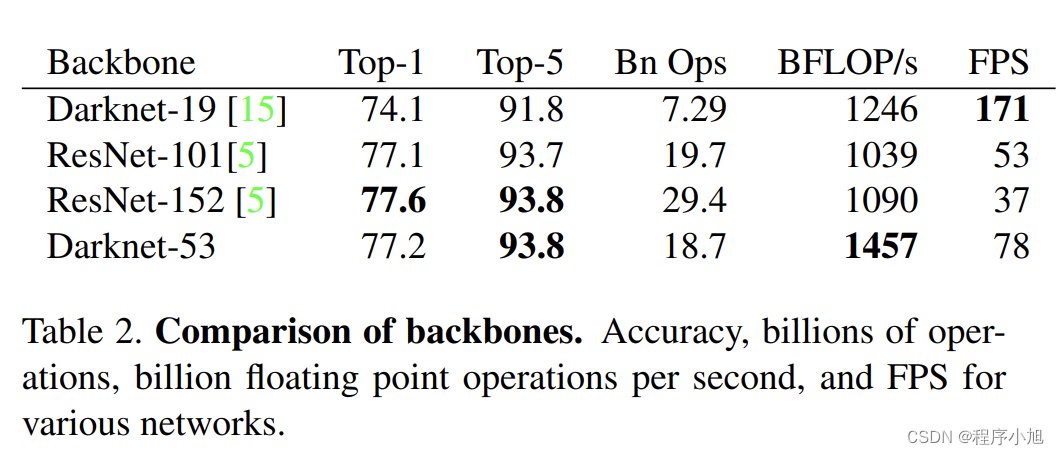
其网络结构为:
2 + ( 1 × 2 ) + 1 + ( 2 × 2 ) + 1 + ( 8 × 2 ) + 1 + ( 8 × 2 ) + 1 + ( 4 × 2 ) + 1 = 53 \begin{array}{l} 2+ \\ (1 \times 2)+1+ \\ (2 \times 2)+1+ \\ (8 \times 2)+1+ \\ (8 \times 2)+1+ \\ (4 \times 2)+1=53 \end{array} 2+(1×2)+1+(2×2)+1+(8×2)+1+(8×2)+1+(4×2)+1=53
其中在网络结构这里论文中给出了锚框的一些设定的尺寸,并对得到的参数进行了解释。
On the COCO dataset the 9 clusters were:
(10×13),(16×30),(33×23),(30×61),(62×45),(59×119),(116 × 90),(156 × 198),(373 × 326).
N × N × [3 ∗ (4 + 1 + 80)] for the 4 bounding box offsets,
1 objectness prediction, and 80 class predictions.
首先有80个类别信息,4个位置信息和yolo中特有的一个confidence参数。
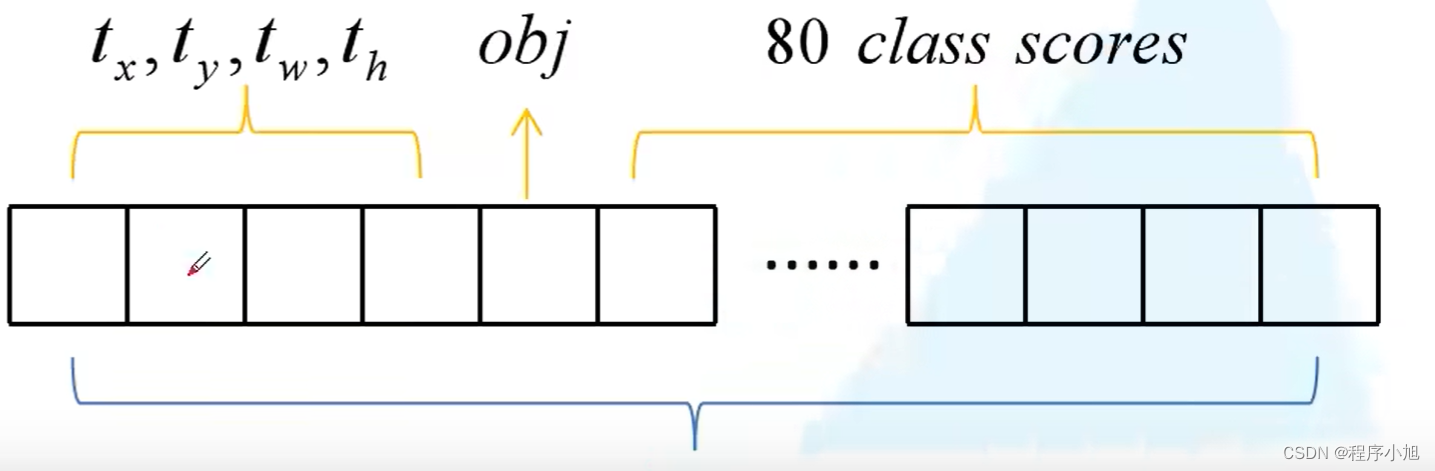
一个锚框就包括了85个参数信息。
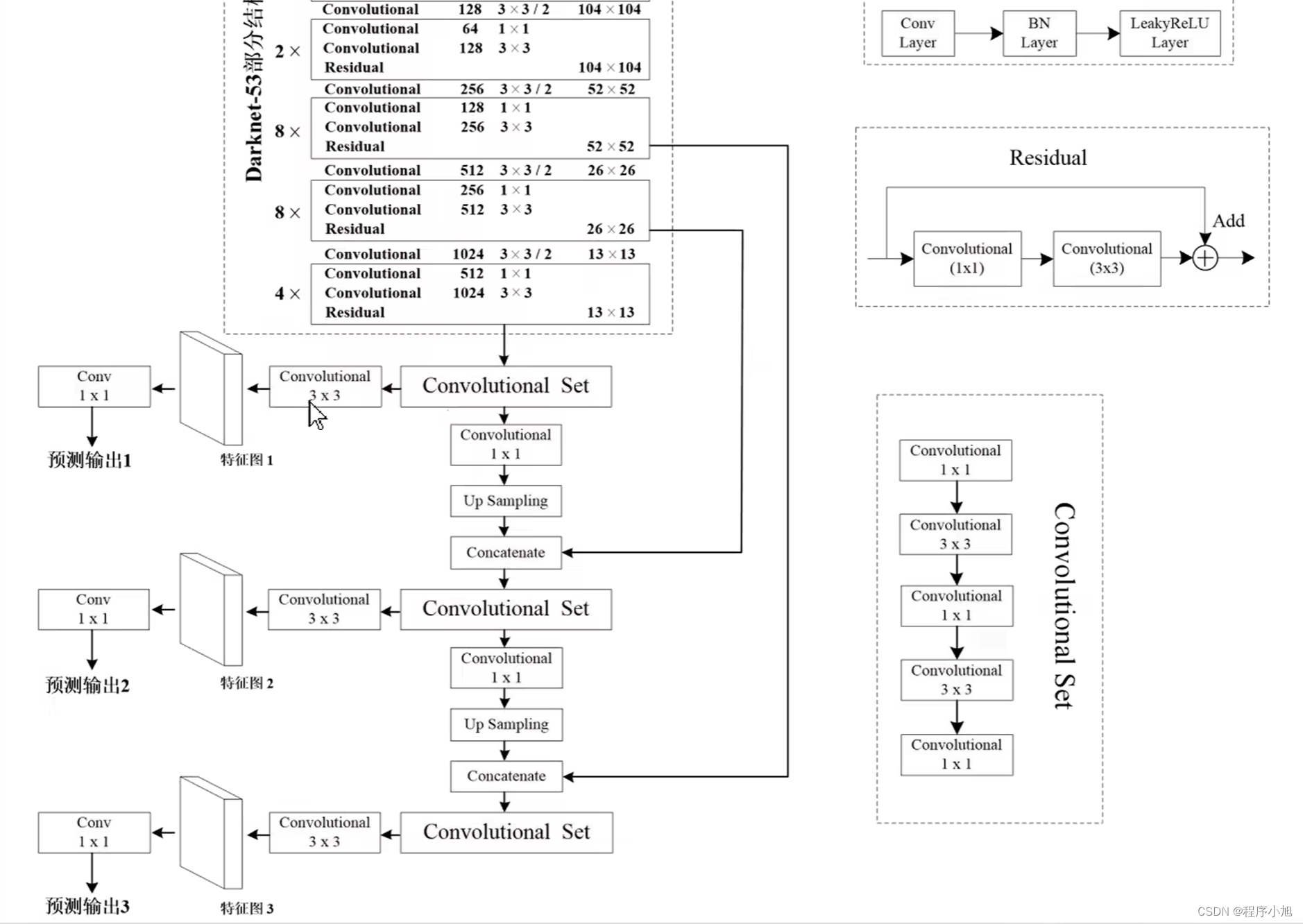
目标边界框的预测
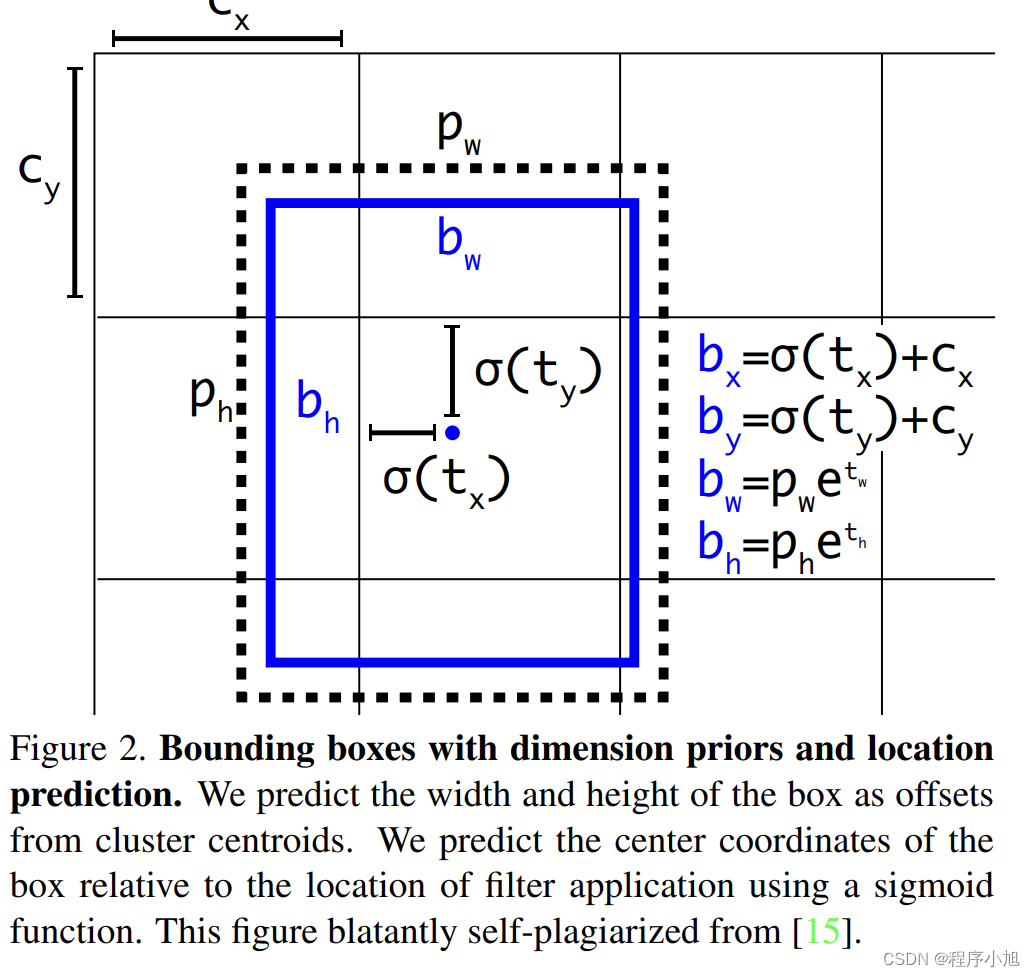
σ ( x ) = Sigmoid ( x ) \sigma(x)=\operatorname{Sigmoid}(x) σ(x)=Sigmoid(x)
将预测的边界框中心限制在当前cell中。
与之前的FasterRCNN不同的是边界框的回归并不是基于锚框的而是相对与当前网格的左上角点的。
其中的tx ty tw th是预测所给出的坐标的参数信息。
b x = σ ( t x ) + c x b y = σ ( t y ) + c y b w = p w e t w b h = p h e t n \begin{array}{l} b_{x}=\sigma\left(t_{x}\right)+c_{x} \\ b_{y}=\sigma\left(t_{y}\right)+c_{y} \\ b_{w}=p_{w} e^{t_{w}} \\ b_{h}=p_{h} \mathrm{e}^{t_{n}} \end{array} bx=σ(tx)+cxby=σ(ty)+cybw=pwetwbh=phetn
从而得到最终预测的中心点的坐标和宽高值
损失函数
L ( o , c , O , C , l , g ) = λ 1 L conf ( o , c ) + λ 2 L c l a ( O , C ) + λ 3 L l o c ( l , g ) L(o, c, O, C, l, g)=\lambda_{1} L_{\text {conf }}(o, c)+\lambda_{2} L_{c l a}(O, C)+\lambda_{3} L_{l o c}(l, g) L(o,c,O,C,l,g)=λ1Lconf (o,c)+λ2Lcla(O,C)+λ3Lloc(l,g)
λ 1 , λ 2 , λ 3 为平衡系数。 \lambda_{1}, \lambda_{2}, \lambda_{3}为平衡系数。 λ1,λ2,λ3为平衡系数。
损失函数同样包括了三个损失分别为:置信度损失,分类损失,定位损失。
- 置信度损失使用的是二值交叉熵损失:
YOLOv3 predicts an objectness score for each bounding
box using logistic regression.This should be1if thebound-lng
g box prior overlaps a ground truth object by more than
any other bounding box prior. If the bounding box prior
Binary Cross Entropy
L conf ( o , c ) = − ∑ i ( o i ln ( c ^ i ) + ( 1 − o i ) ln ( 1 − c ^ i ) ) N L_{\text {conf }}(o, c)=-\frac{\sum_{i}\left(o_{i} \ln \left(\hat{c}_{i}\right)+\left(1-o_{i}\right) \ln \left(1-\hat{c}_{i}\right)\right)}{N} Lconf (o,c)=−N∑i(oiln(c^i)+(1−oi)ln(1−c^i))
c ^ i = Sigmoid ( c i ) \hat{c}_{i}=\operatorname{Sigmoid}\left(c_{i}\right) c^i=Sigmoid(ci)
其中oi,∈[0,1],表示预测目标边界框与真实目标边界框的IOU
c为预测值,ci,为c通过Sigmoid函数得到的预测置信度。N为正负样本个数。
- 类别损失使用的是二值交叉熵损失:
L c l a ( O , C ) = − ∑ i ∈ posj j cla ( O i j ln ( C ^ i j ) + ( 1 − O i j ) ln ( 1 − C ^ i j ) ) N pos C ^ i j = Sigmoid ( C i j ) \begin{array}{c} L_{c l a}(O, C)=-\frac{\sum_{i \in \text { posj } j \text { cla }}\left(O_{i j} \ln \left(\hat{C}_{i j}\right)+\left(1-O_{i j}\right) \ln \left(1-\hat{C}_{i j}\right)\right)}{N_{\text {pos }}} \\ \hat{C}_{i j}=\operatorname{Sigmoid}\left(C_{i j}\right) \end{array} Lcla(O,C)=−Npos ∑i∈ posj j cla (Oijln(C^ij)+(1−Oij)ln(1−C^ij))C^ij=Sigmoid(Cij)
其中Oij∈{0,1},表示预测目标边界框i中是否存在第j类目标存在则为1
Cij为预测值,Cij(hat)为Cij通过Sigmoid函数得到的目标概率
Npos为正样本个数
- 定位损失
L loc ( t , g ) = ∑ i ∈ pos ( σ ( t x i ) − g ^ x i ) 2 + ( σ ( t y i ) − g ^ y i ) 2 + ( t w i − g ^ w i ) 2 + ( t h i − g ^ h i ) 2 N pos L_{\text {loc }}(t, g)=\frac{\sum_{i \in \text { pos }}\left(\sigma\left(t_{x}^{i}\right)-\hat{g}_{x}^{i}\right)^{2}+\left(\sigma\left(t_{y}^{i}\right)-\hat{g}_{y}^{i}\right)^{2}+\left(t_{w}^{i}-\hat{g}_{w}^{i}\right)^{2}+\left(t_{h}^{i}-\hat{g}_{h}^{i}\right)^{2}}{N_{\text {pos }}} Lloc (t,g)=Npos ∑i∈ pos (σ(txi)−g^xi)2+(σ(tyi)−g^yi)2+(twi−g^wi)2+(thi−g^hi)2
g
^
x
i
=
g
x
i
−
c
x
i
g
^
y
i
=
g
y
i
−
c
y
i
g
^
w
i
=
ln
(
g
w
i
/
p
w
i
)
g
^
h
i
=
ln
(
g
h
i
/
p
h
i
)
\begin{array}{l} \hat{g}_{x}^{i}=g_{x}^{i}-c_{x}^{i} \\ \hat{g}_{y}^{i}=g_{y}^{i}-c_{y}^{i} \\ \hat{g}_{w}^{i}=\ln \left(g_{w}^{i} / p_{w}^{i}\right) \\ \hat{g}_{h}^{i}=\ln \left(g_{h}^{i} / p_{h}^{i}\right) \end{array}
g^xi=gxi−cxig^yi=gyi−cyig^wi=ln(gwi/pwi)g^hi=ln(ghi/phi)