视频链接
基本概念
Regression(回归):
类似于填空
Classification(分类):
类似于选择
Structure Learning(机器学习):
??
机器学习找对应函数的步骤
1、写出一个带有未知参数的函数
Model(模型):一个函数,比如y = b + w * x1(y是要预测的,x1是已知的)
weight(权重):上述中的w就是权重
bias(偏移):上述中的b就是偏移
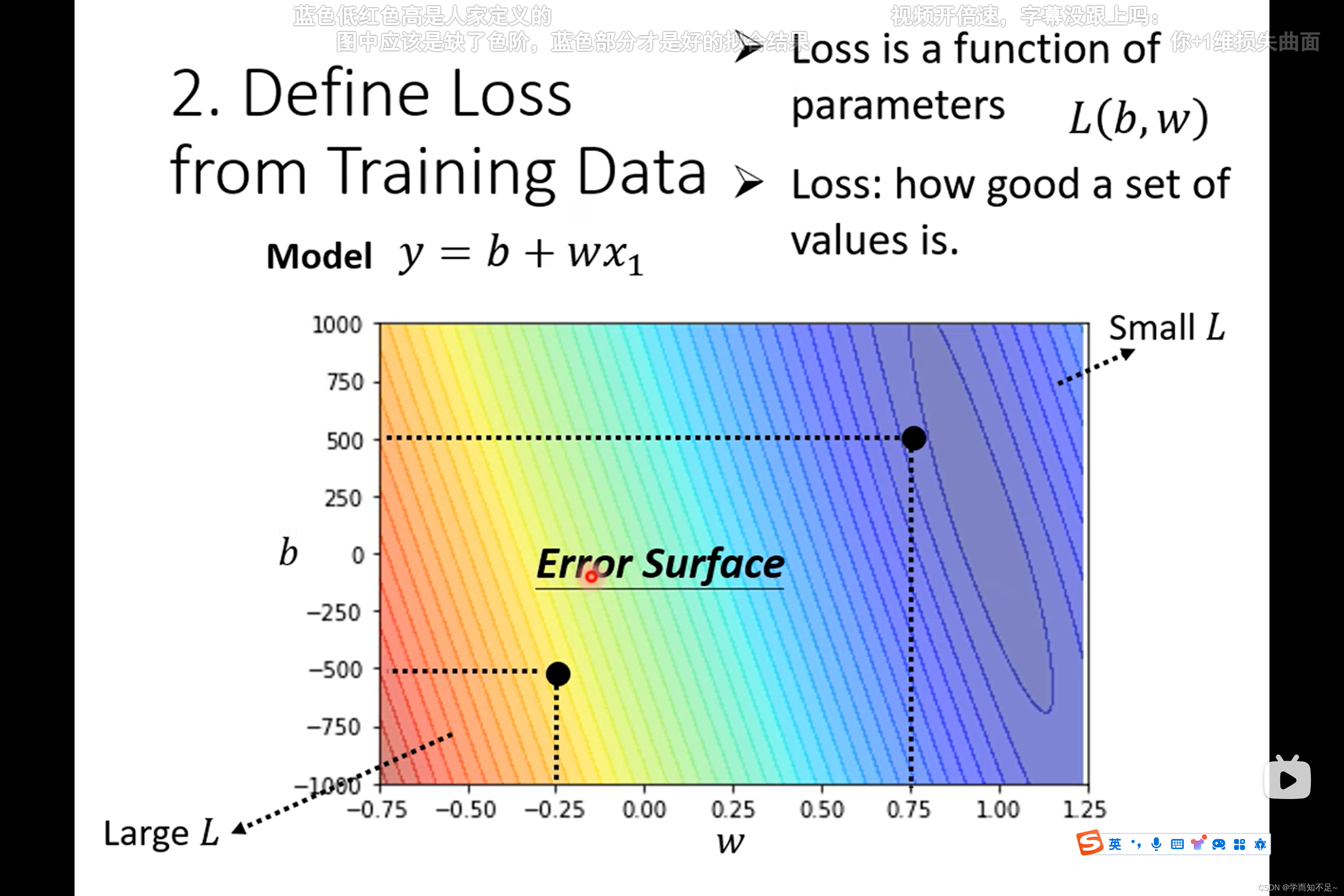
2、定义训练数据的损失函数
loss(损失函数):一个函数,输入是模型中的参数 L(b, w),输出的值代表这组b,w好还是不好,值越大,代表b,w越不好
MAE(mean absolute error): 均值绝对误差
MSE(mean square error): 均值方差
Cross-entropy:如果预测值和实际值都是随机分布的,则使用这种方式查看损失值

label(真实值):真实的值,类似于训练数据
Error surface(误差面):等高线图
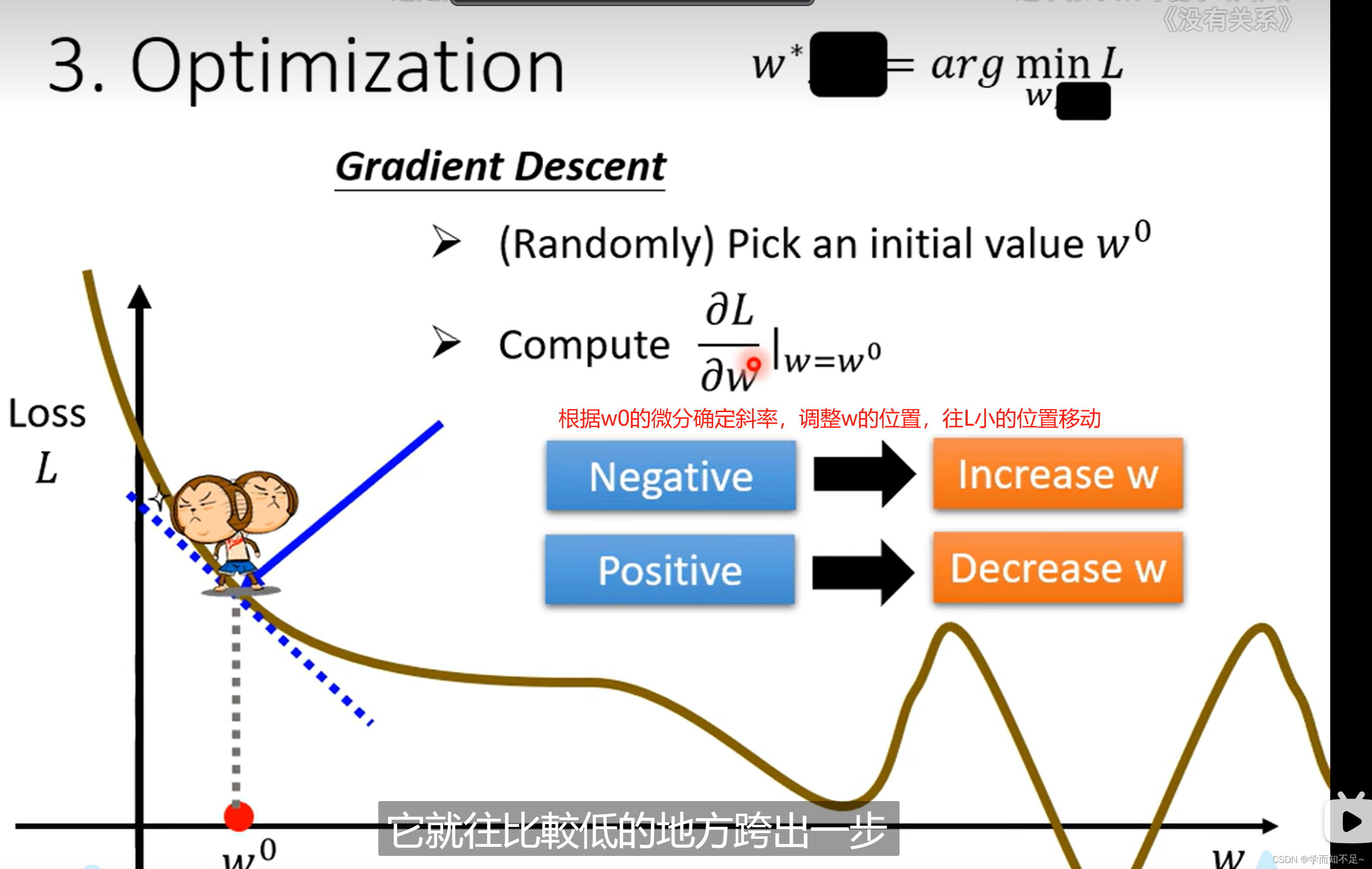
3、Optimization(优化)
找一个w和b,使得Loss结果最小
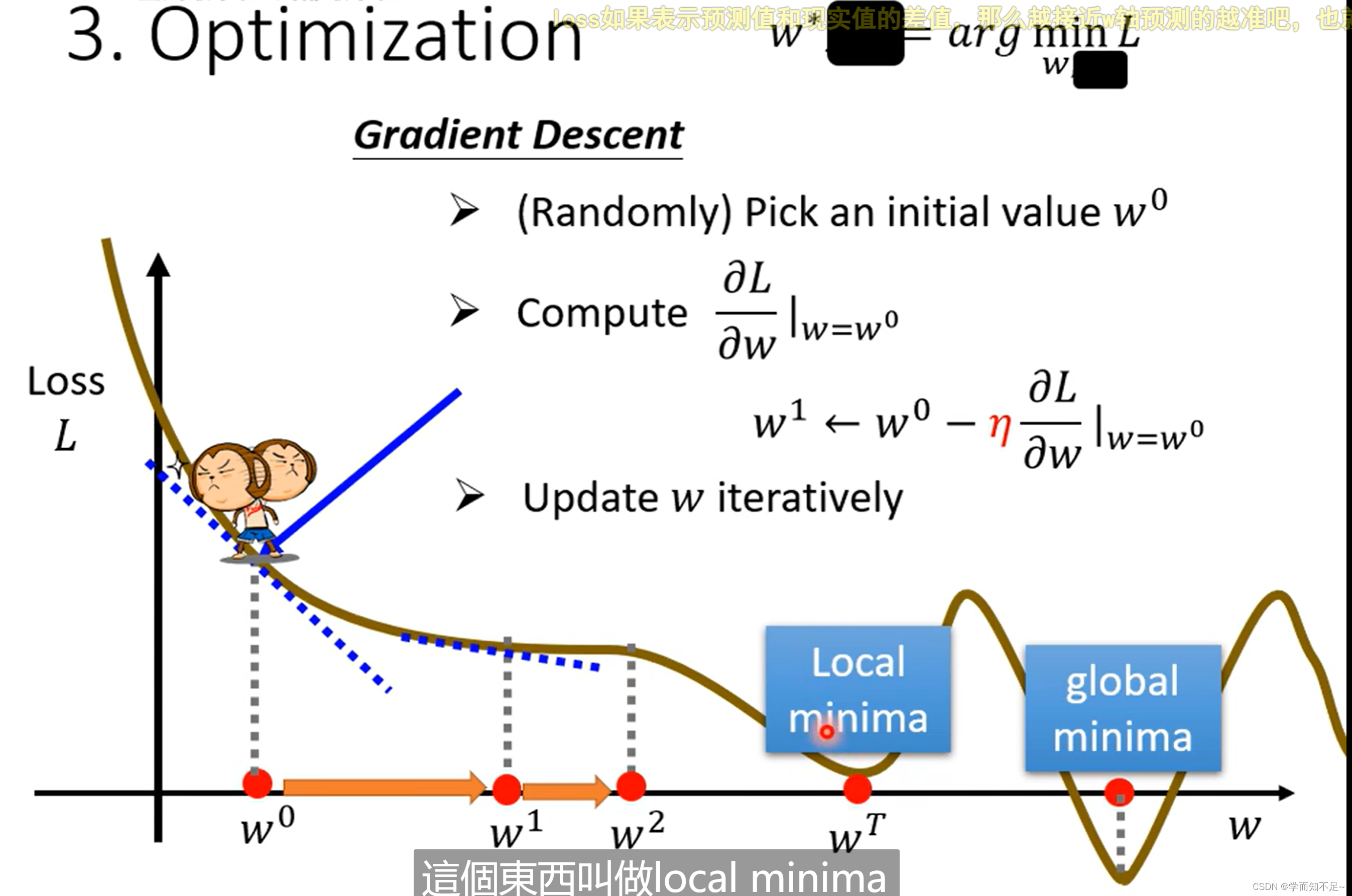
Gradient Descent(梯度下降)

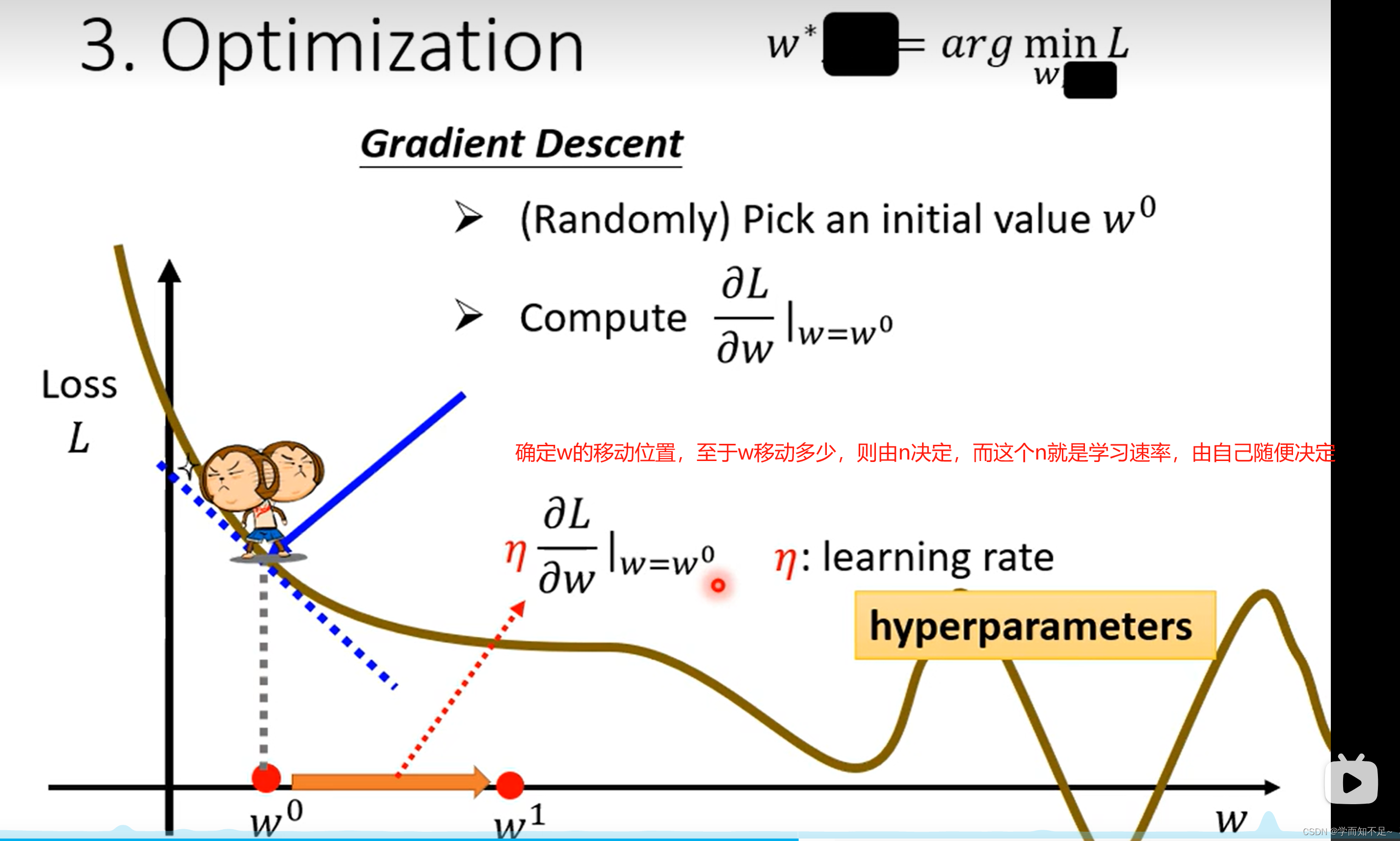
Learning rate:学习速率 n
hyper parameters:超参数 自己设定
local minima局部最优
global minima全局最优
梯度下降有个问题就是容易导致局部最优?其实局部最优是一个假问题!
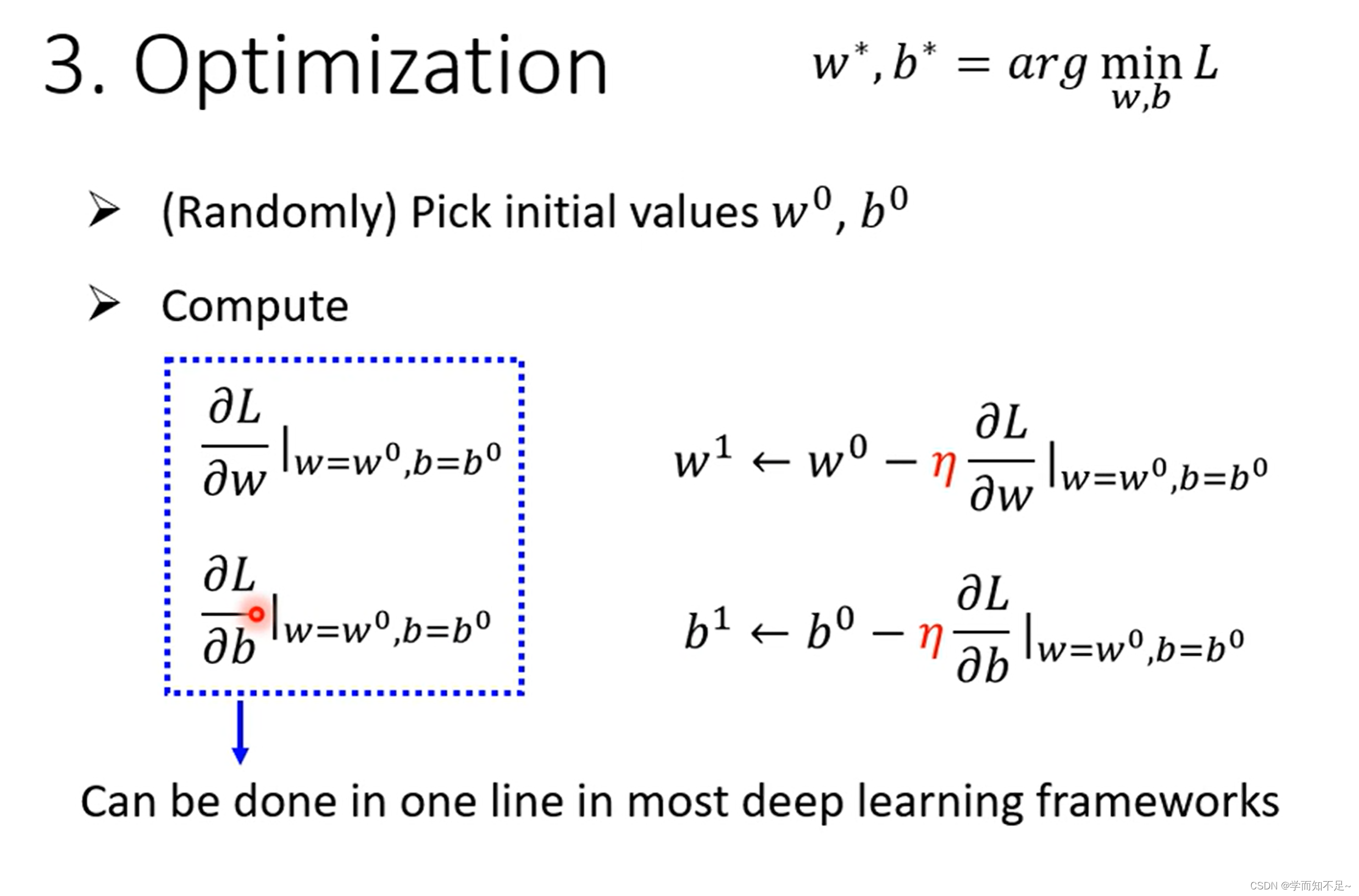
上述说的只是一个参数的情况,实际上多个参数也是一样的做法
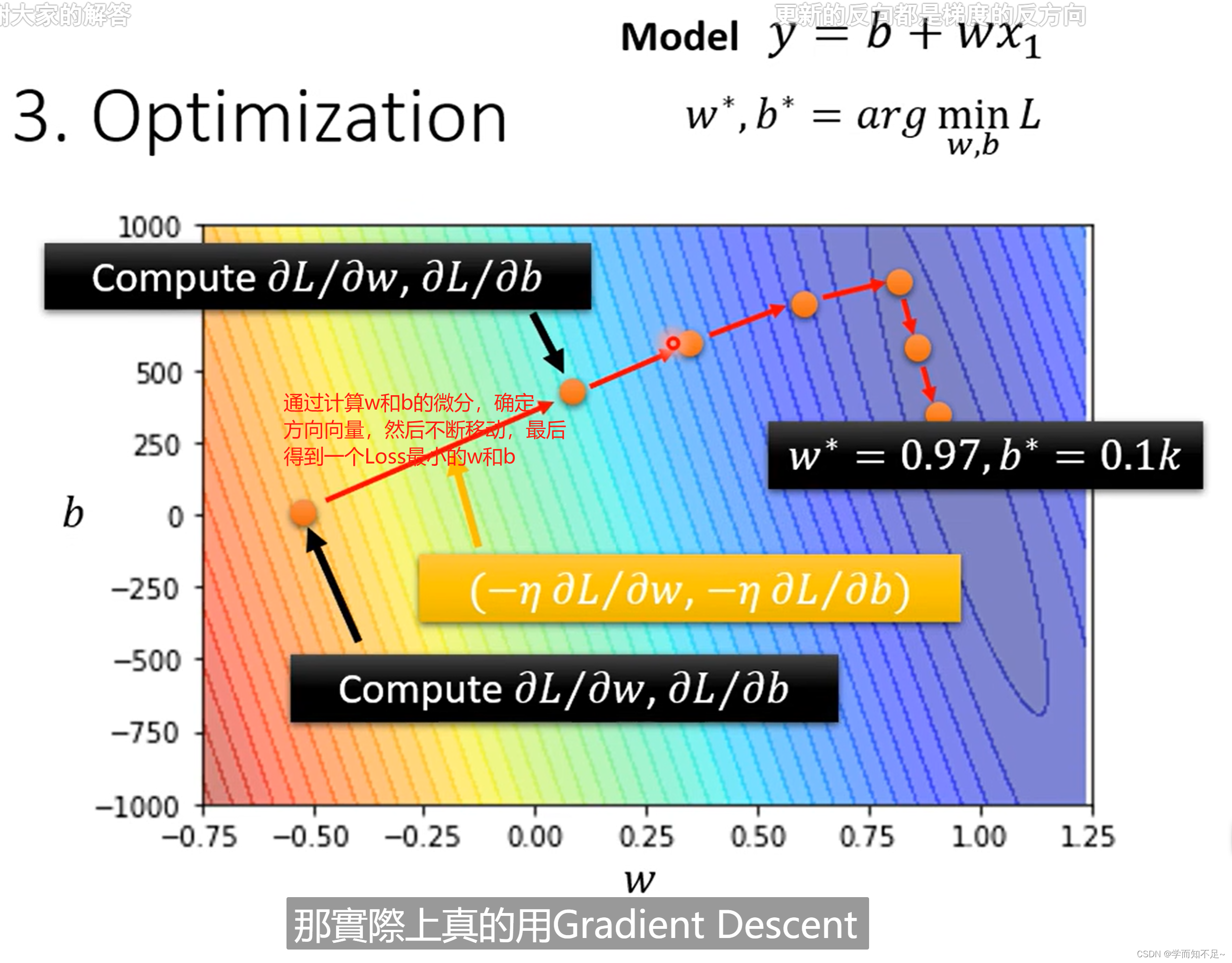
由线性模型推广至非线性模型
前面的步骤统称训练,实际上都是基于已知数据进行的,我们的目的是要通过这个式子预测新的数据

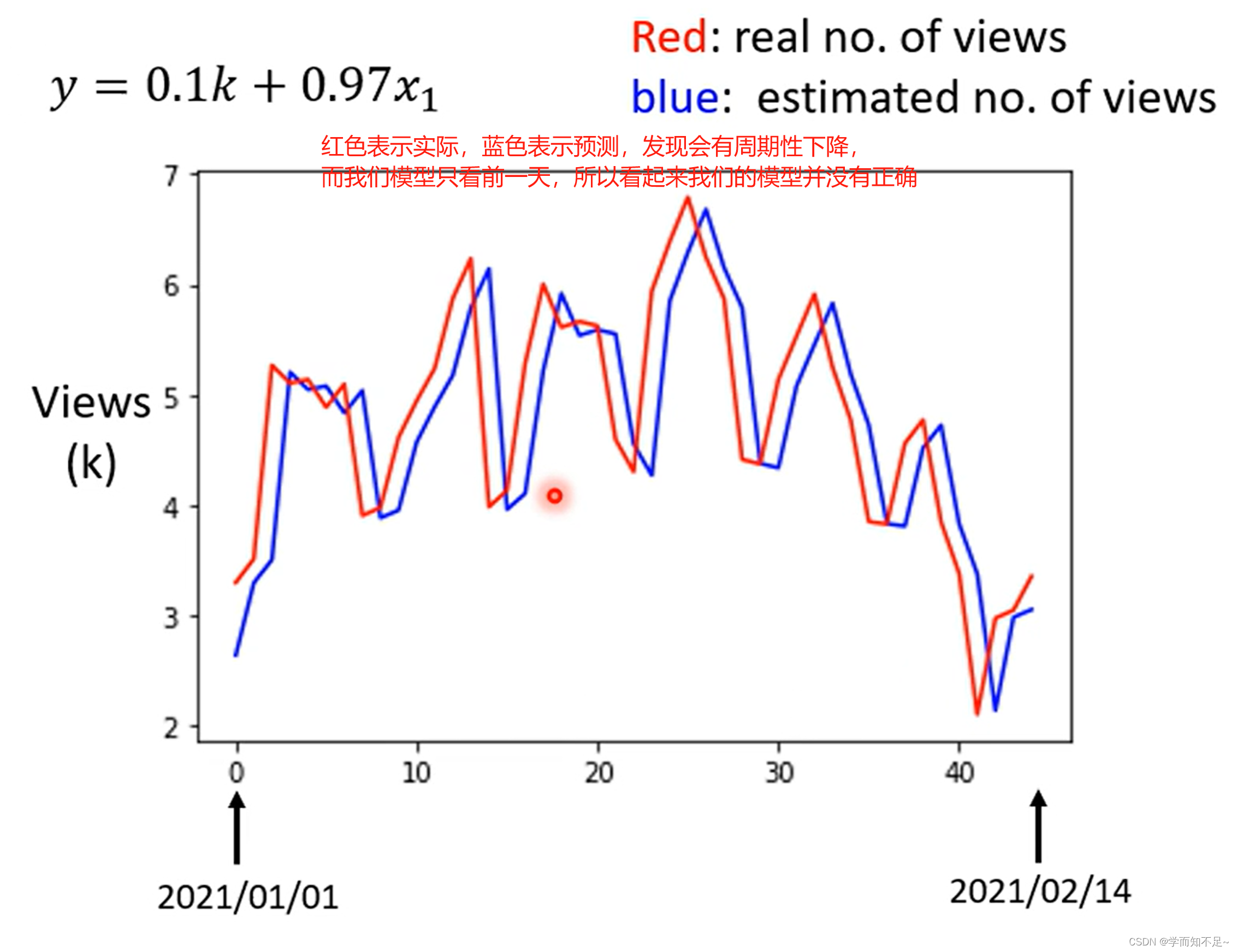
为此,我们应该修改模型,以7天为一个周期来预测
linear models:线性模型,下面如图,就是考虑不同周期对应的线性模型

model bias:模型偏移
与之前说的bias不一样,这里说的是模型本身的限制导致没办法模拟真实的情况
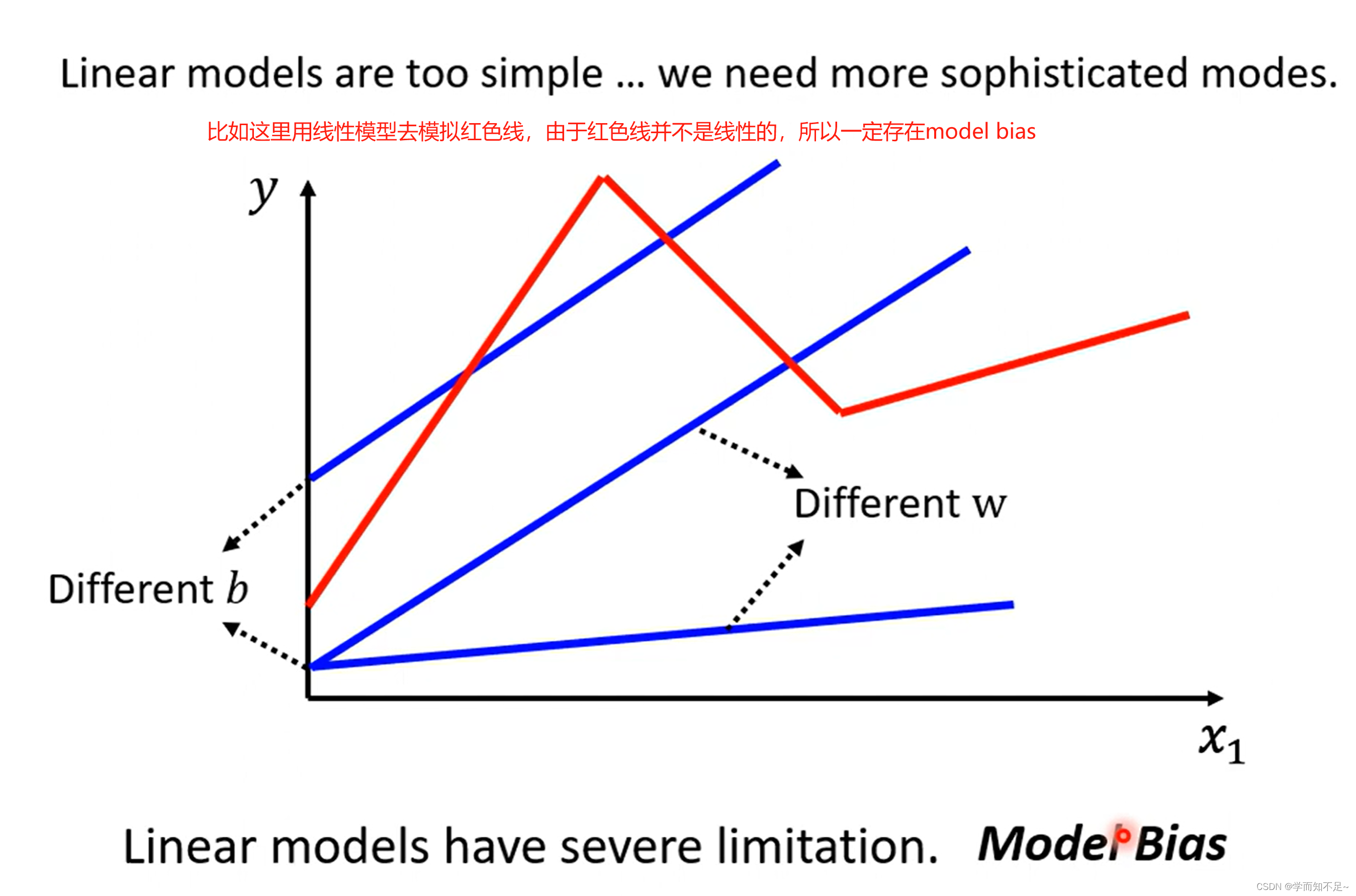
所以我们需要一个更复杂的有未知参数的函数来替代线性模型
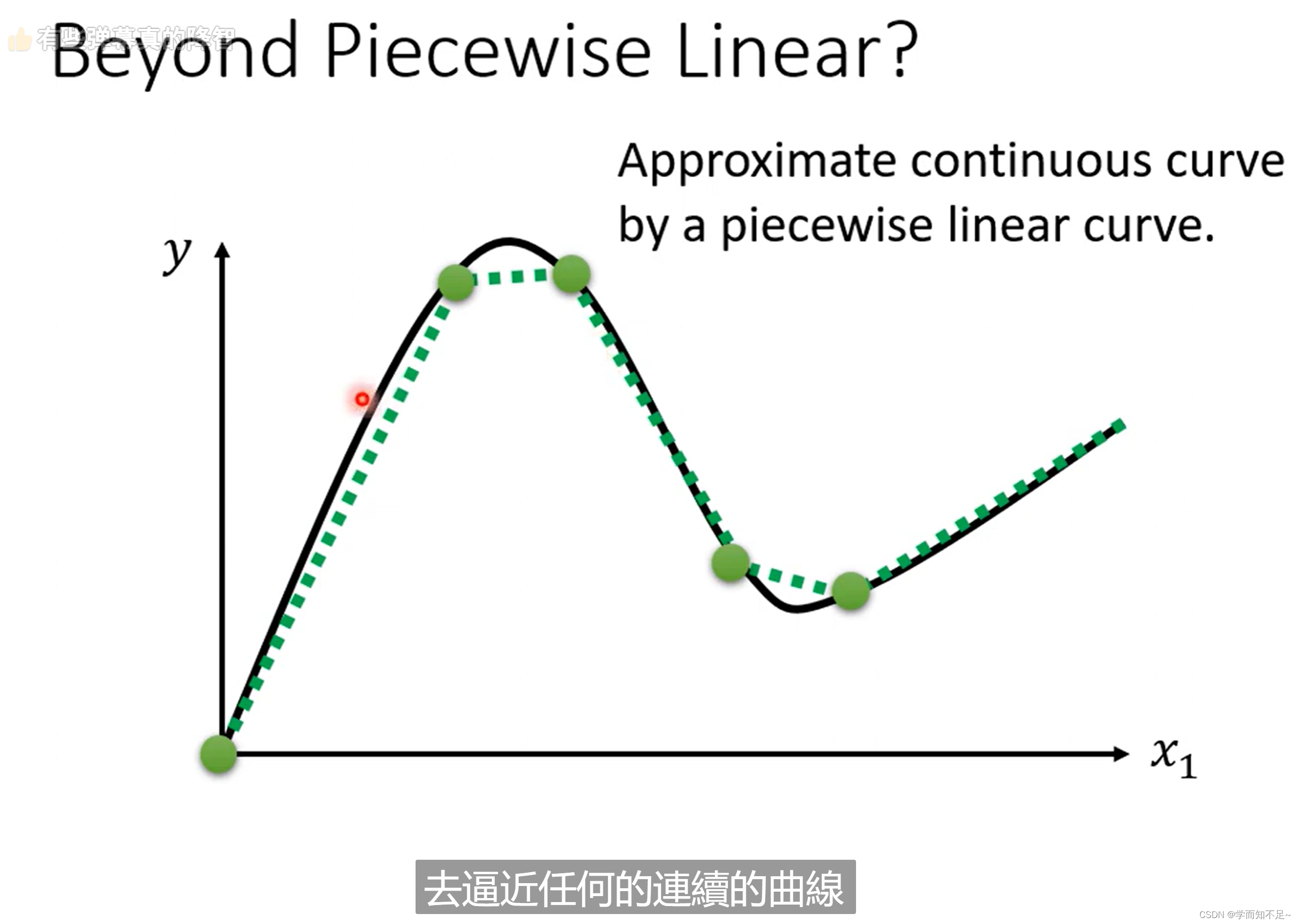
piecewise linear curves:分段线性曲线
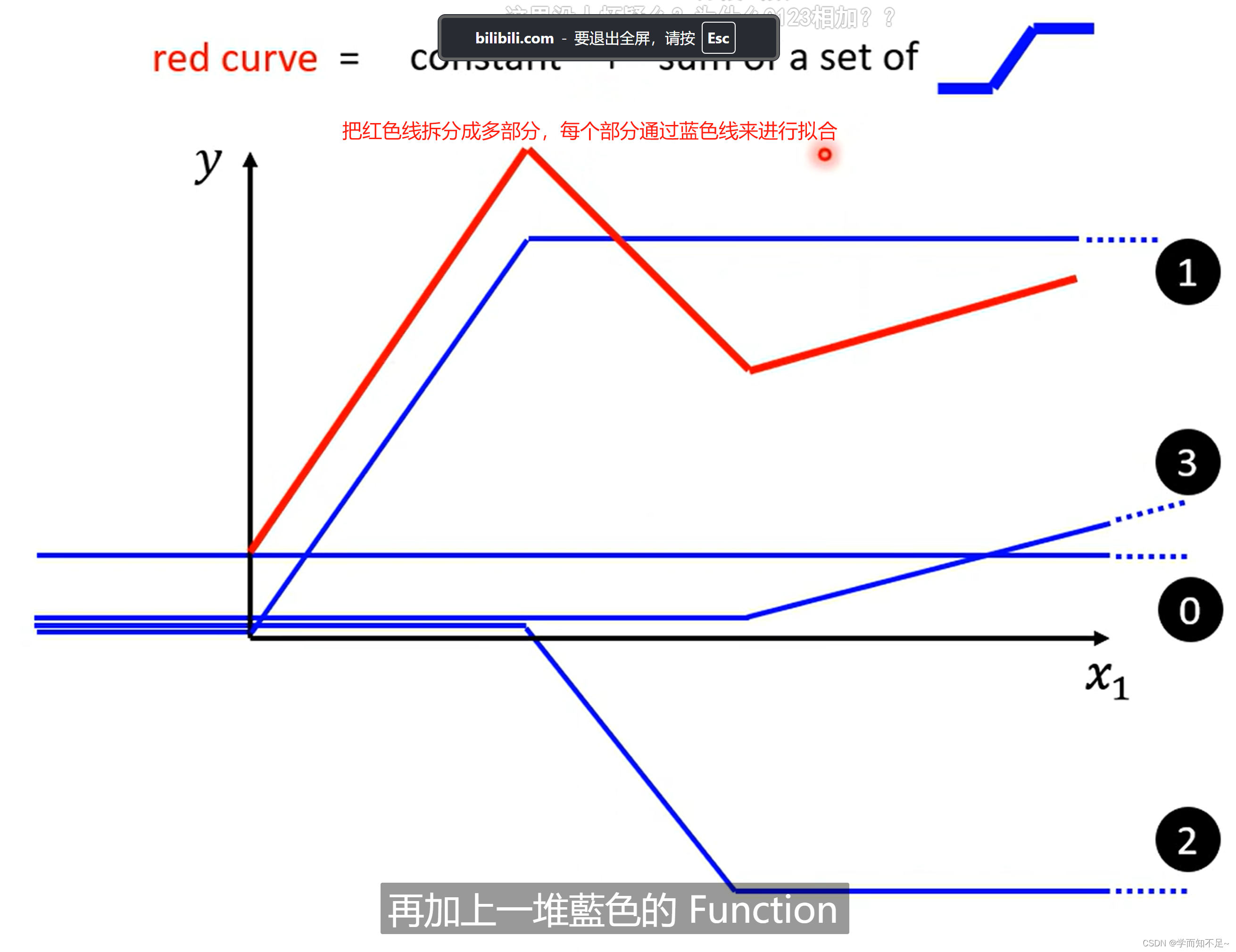
这里面哪怕红色线不是线性的,而是曲线的,我们也可以通过微分的方式,选取足够多的点将其看成是线性的
那蓝色线的函数该怎么写出来呢,有一个很出名的函数叫做sigmoid,虽然是曲线,但是很接近蓝色线
sigmoid:S型线段对应的函数
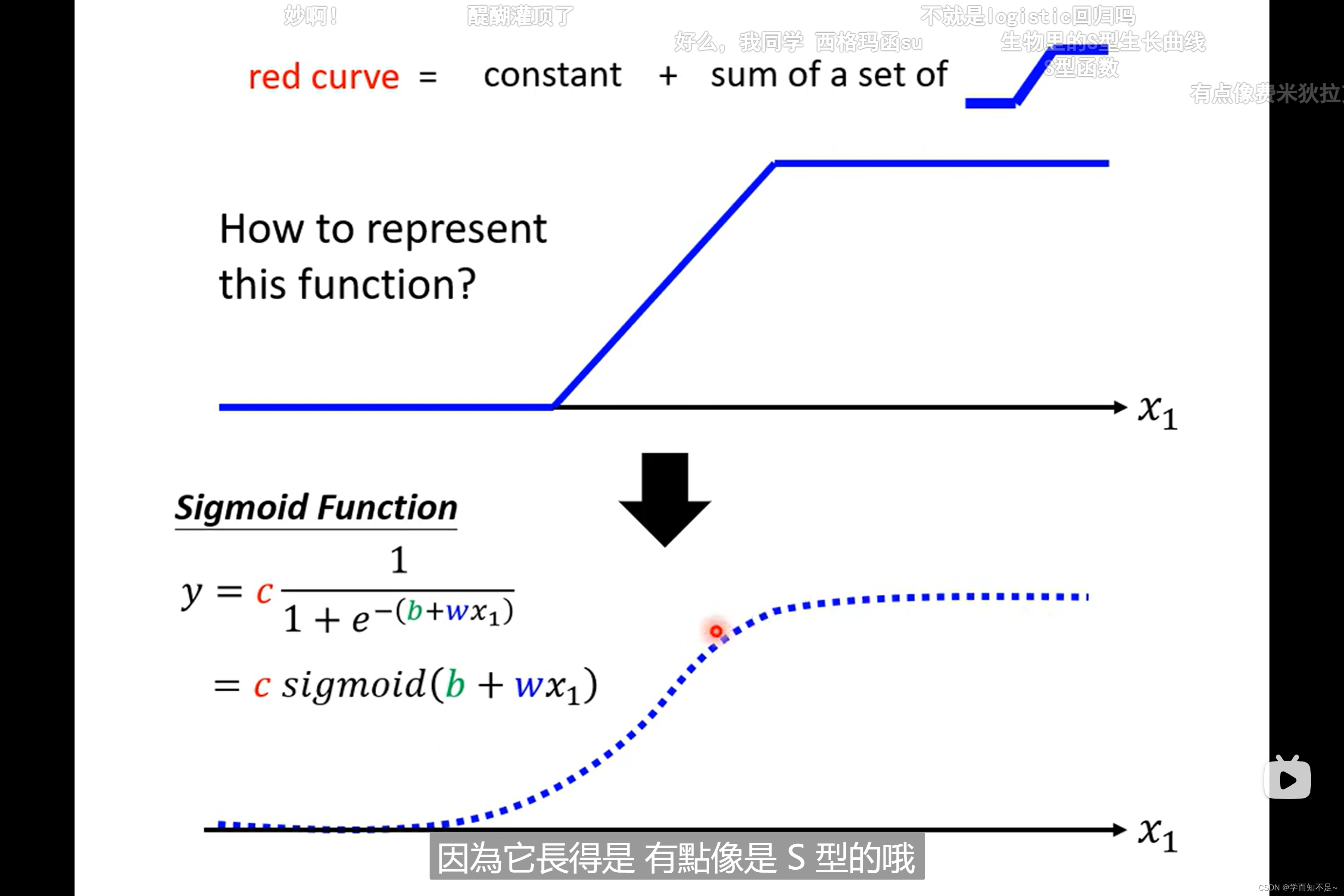
而蓝色线的函数我们一般将其称作hard sigmoid
通过调整c、b、w这三个值,我们可以得到不同的sigmoid函数,从而逼近不同的蓝色线

所以上述的红色线可以通过以下公式逼近:
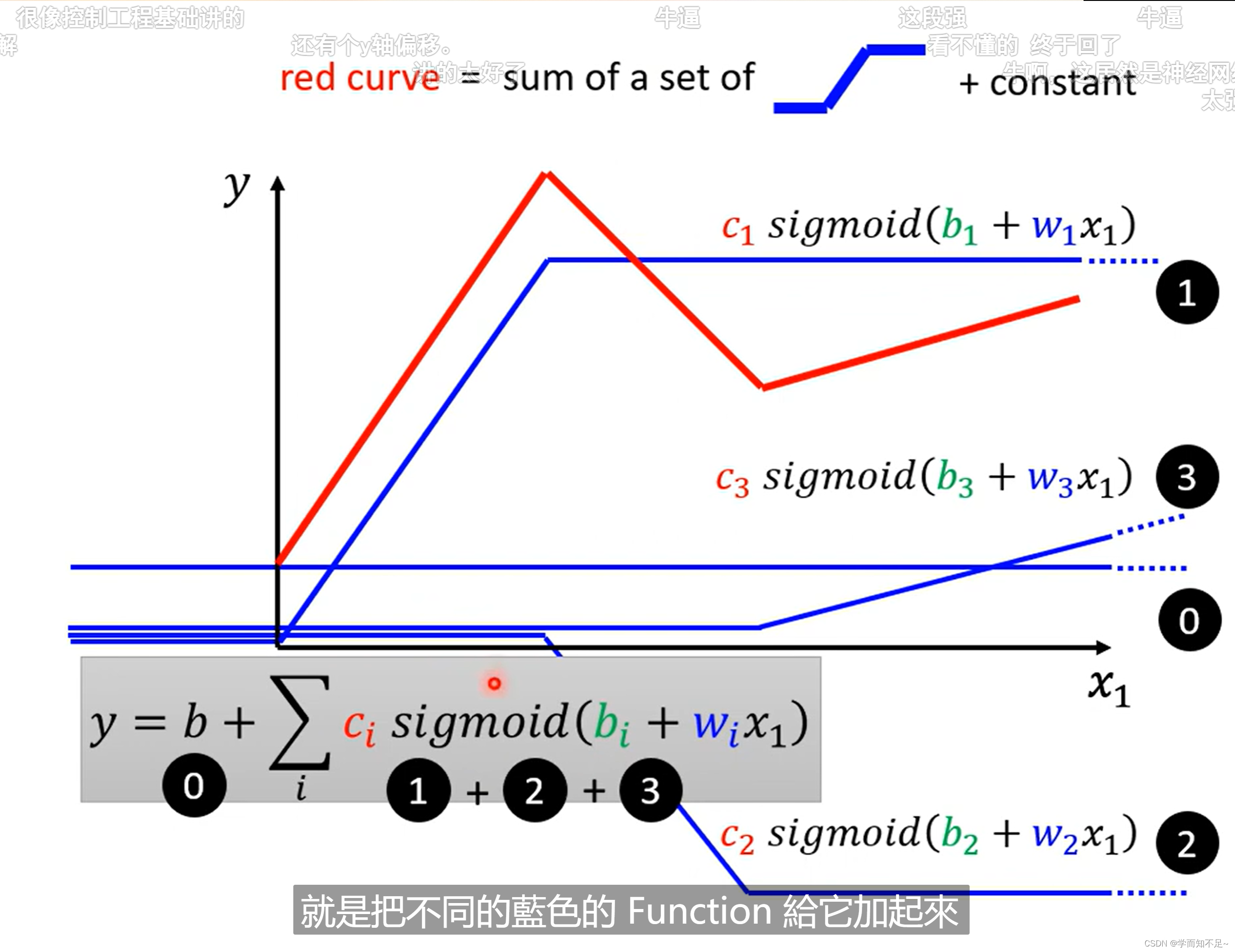
单个特征推广至多个特征

改写机器学习的每一步
1、函数式子转矩阵
上述多个特征的式子可以转成用矩阵的方式表示
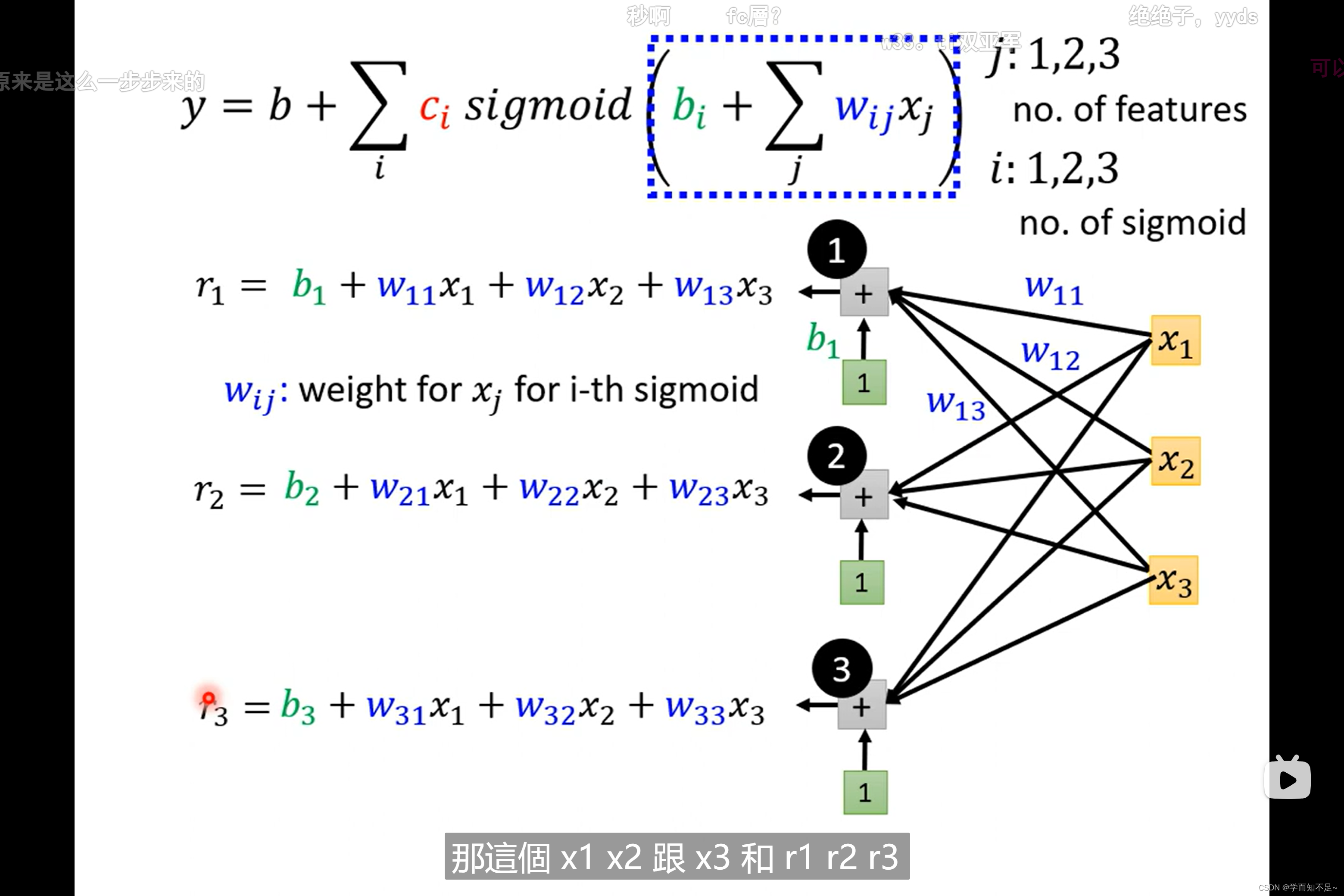

上述已经知道r表示什么,再用a表示sigmoid®
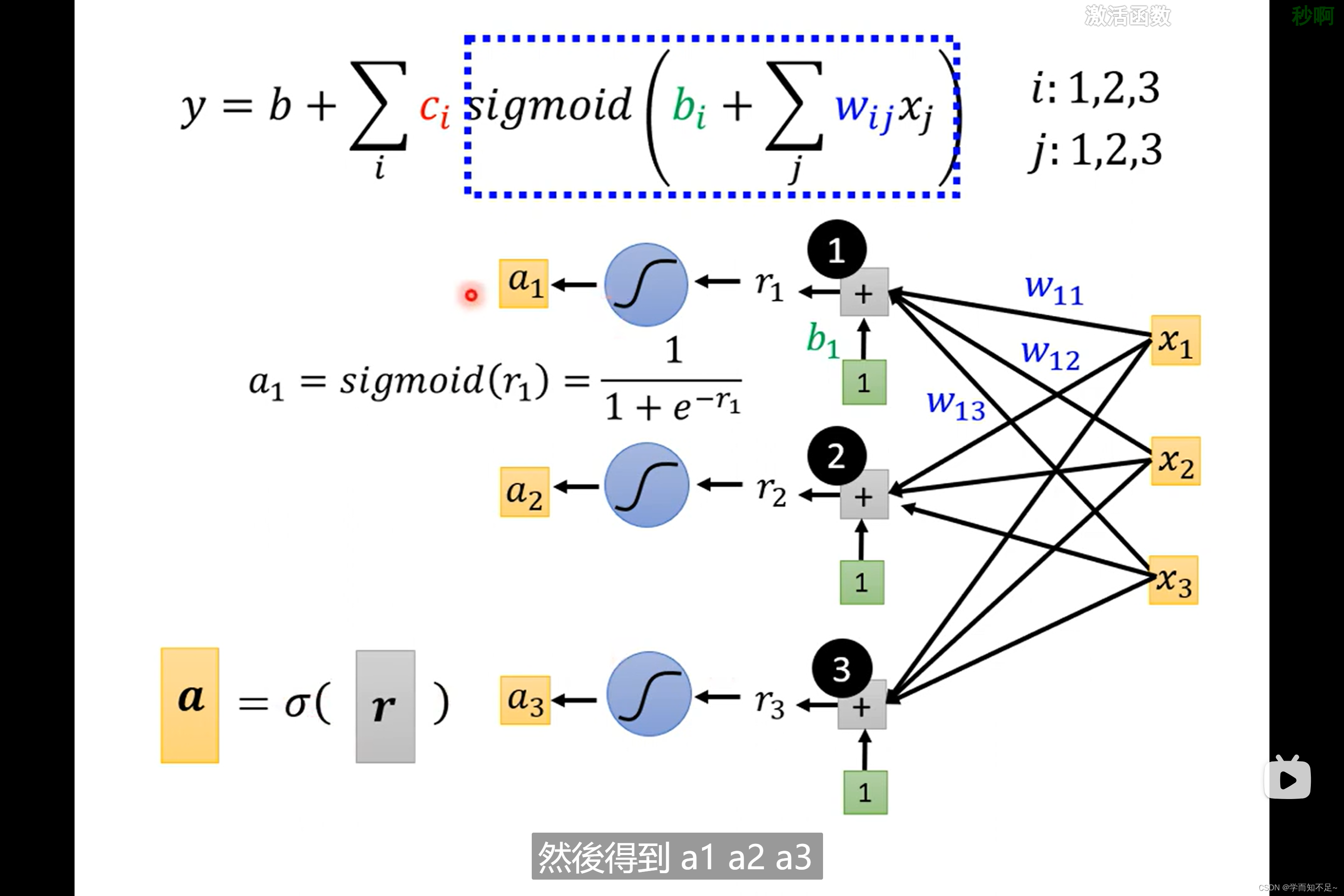
所以最终式子y可以转成向量的表示方式如下所示

总结:
transpose:矩阵转置
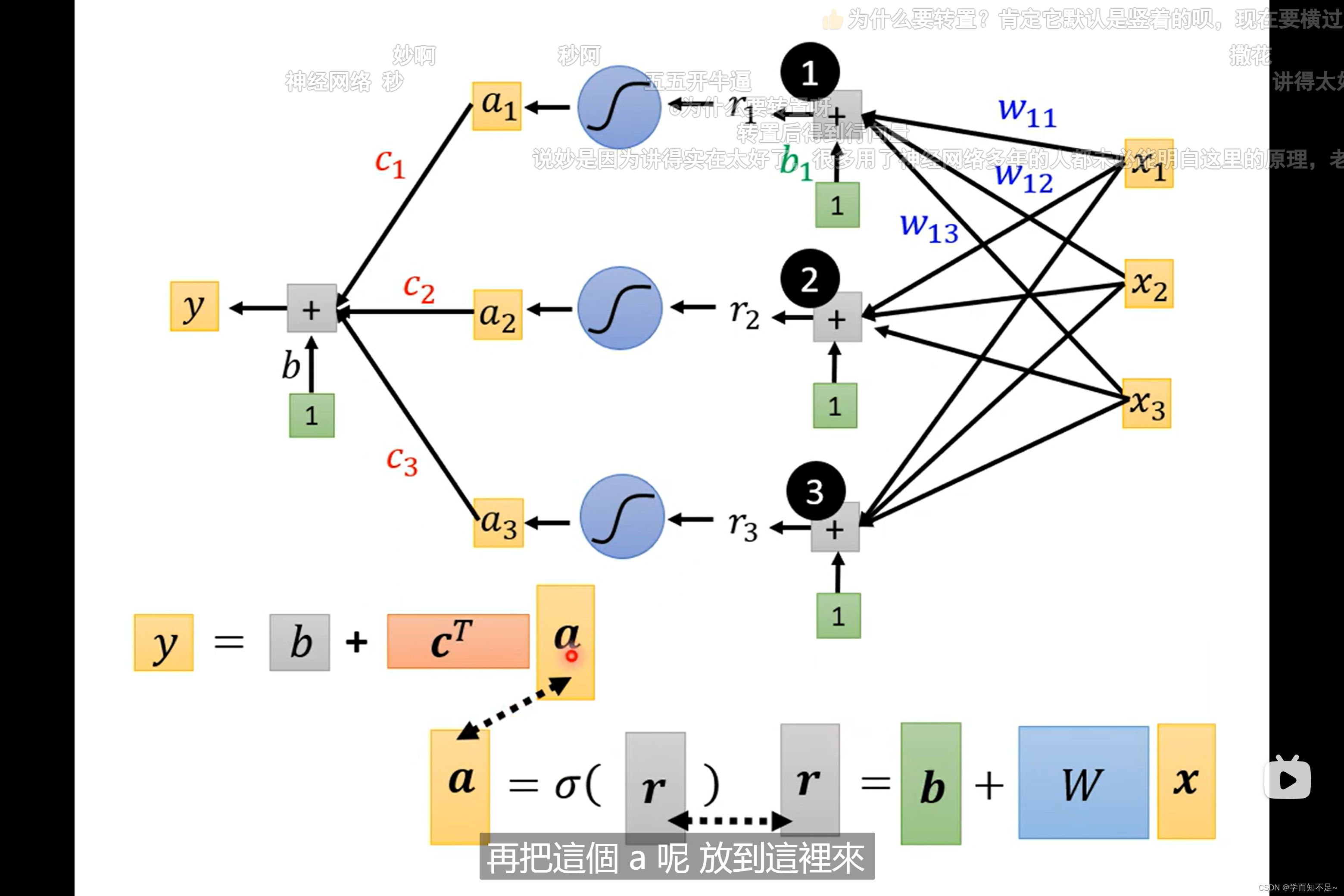
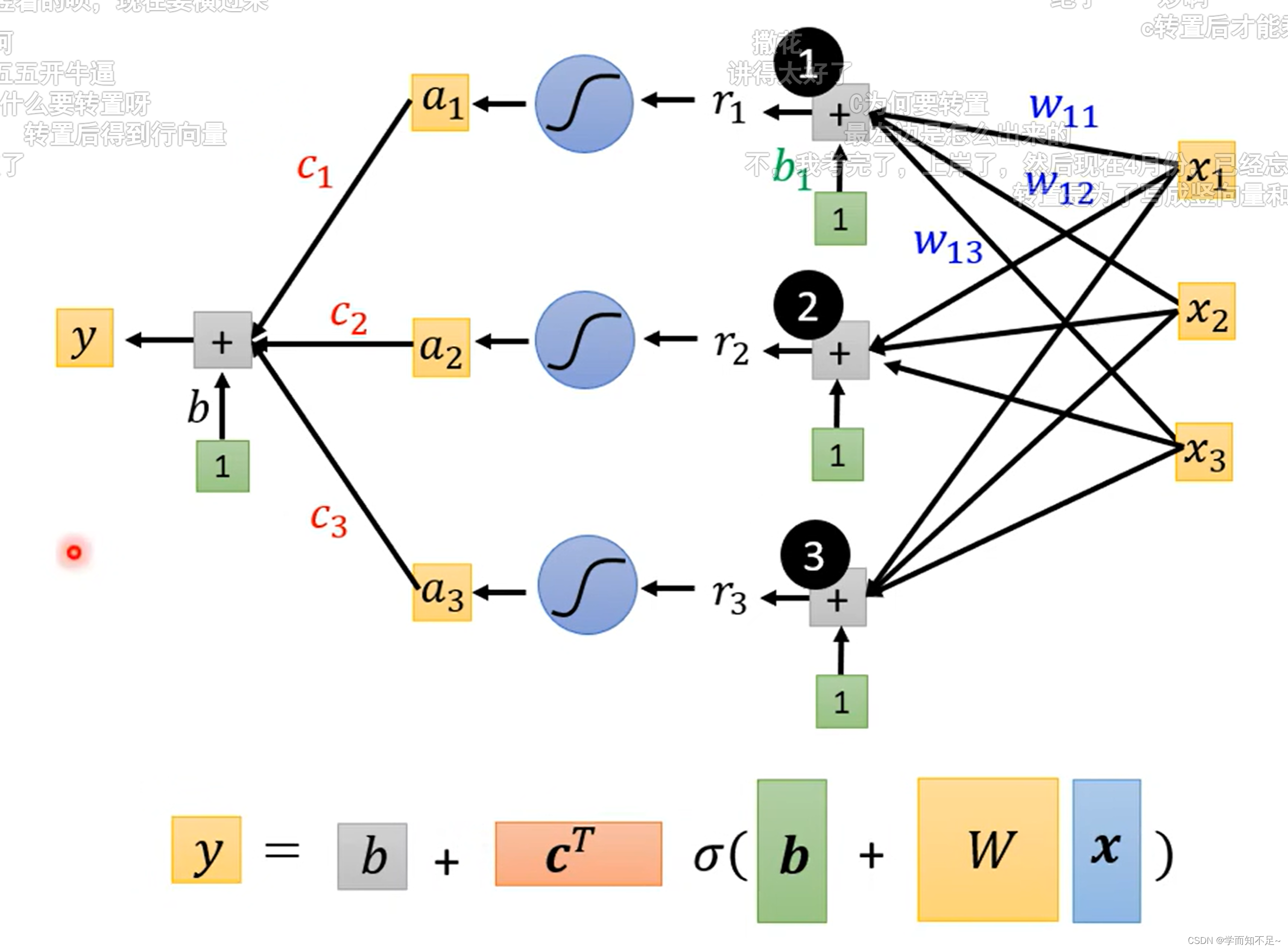
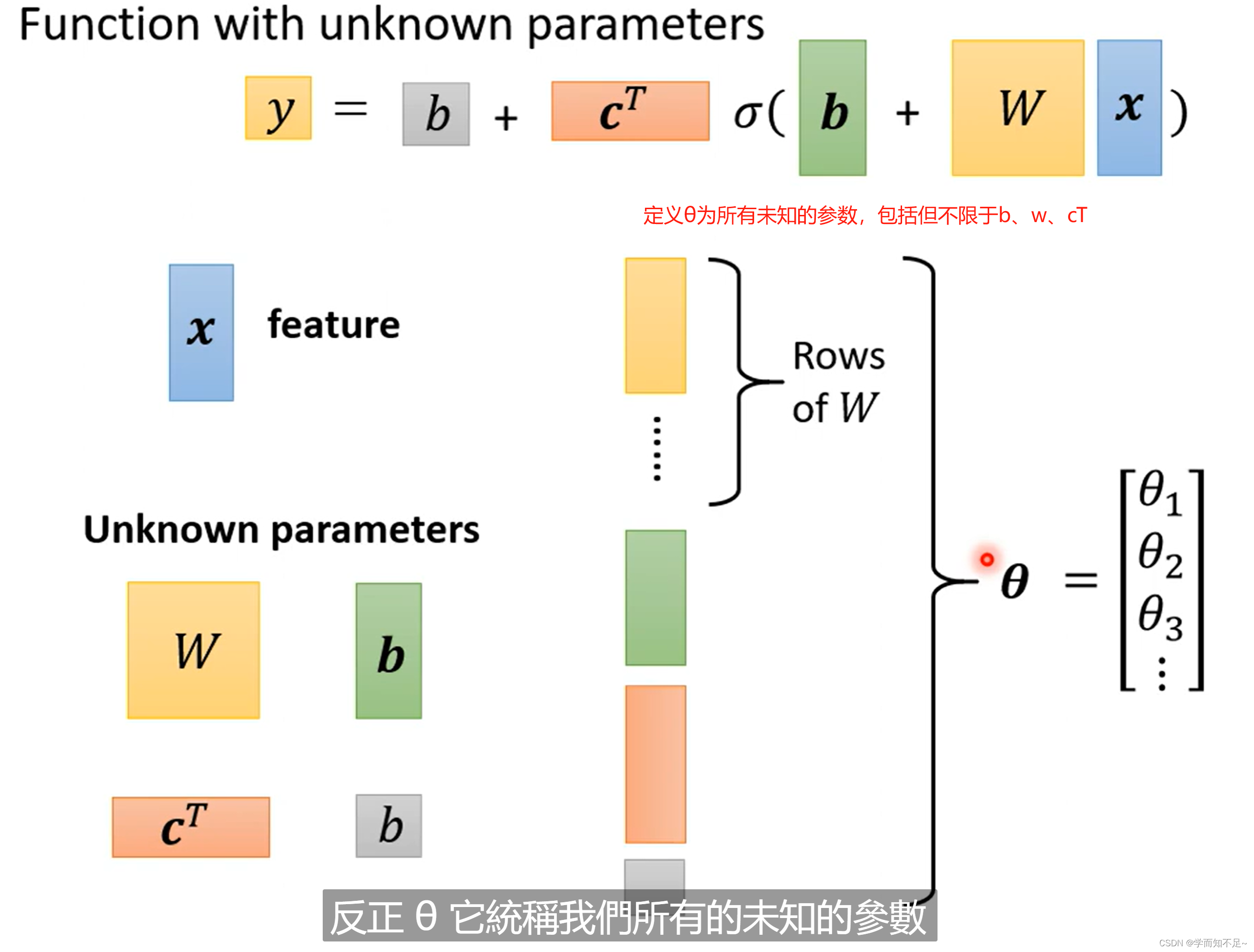
重新定义一下未知参数
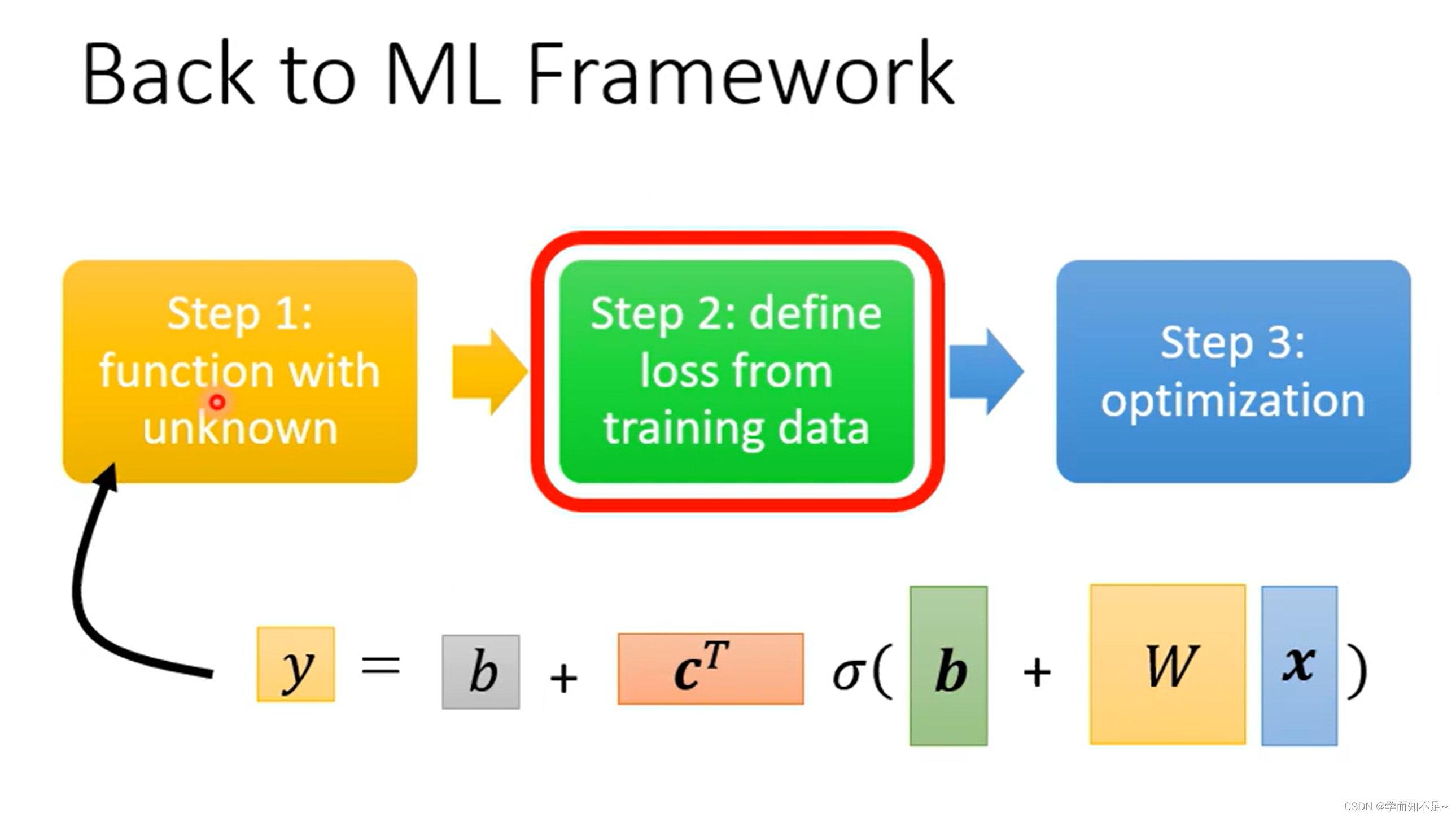
2、重定义Loss函数

3、优化
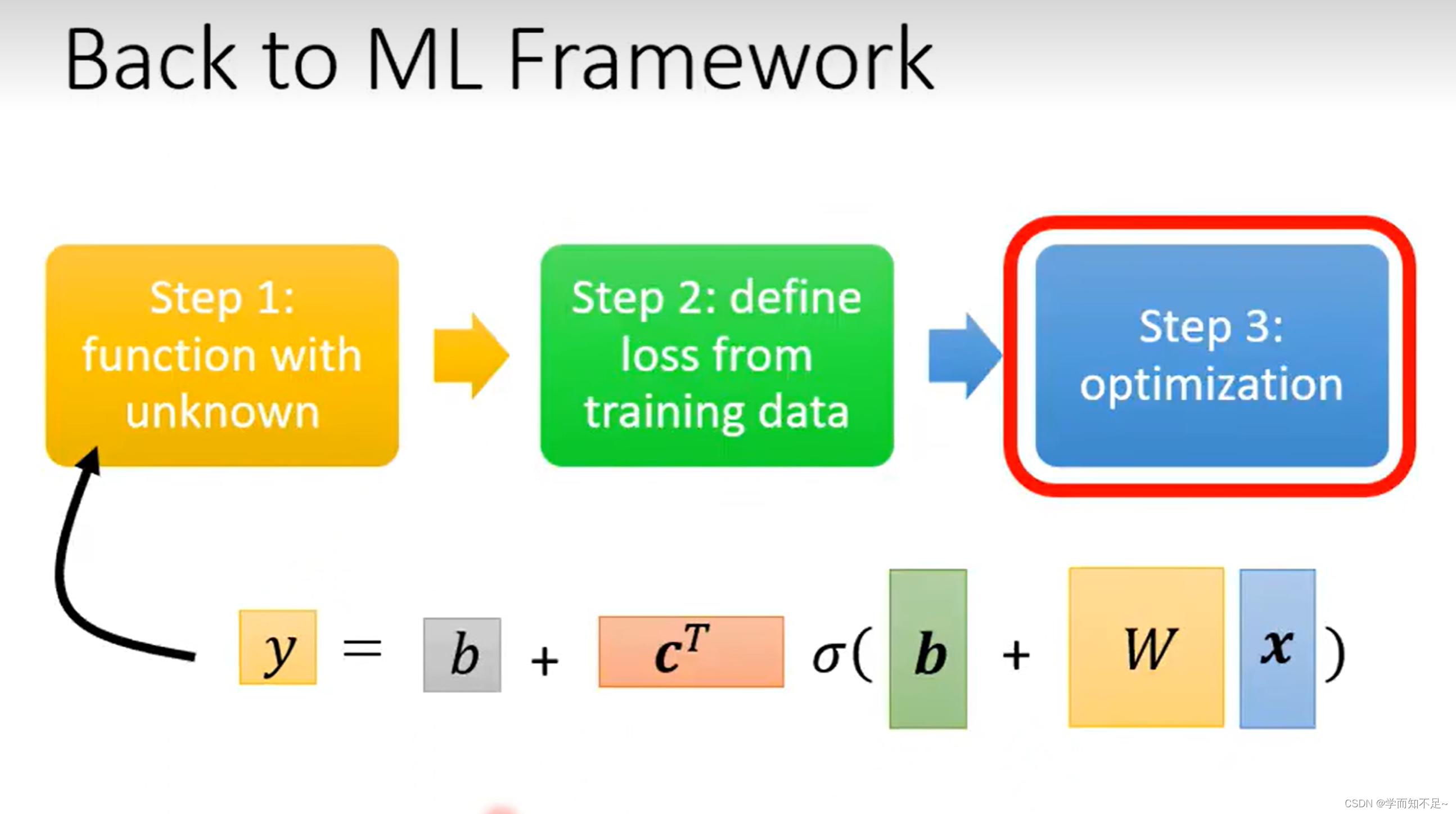
优化步骤没什么区别,还是用梯度下降,唯一就是参数变了,本质上还是前面w,b两个参数的时候情况是一样的


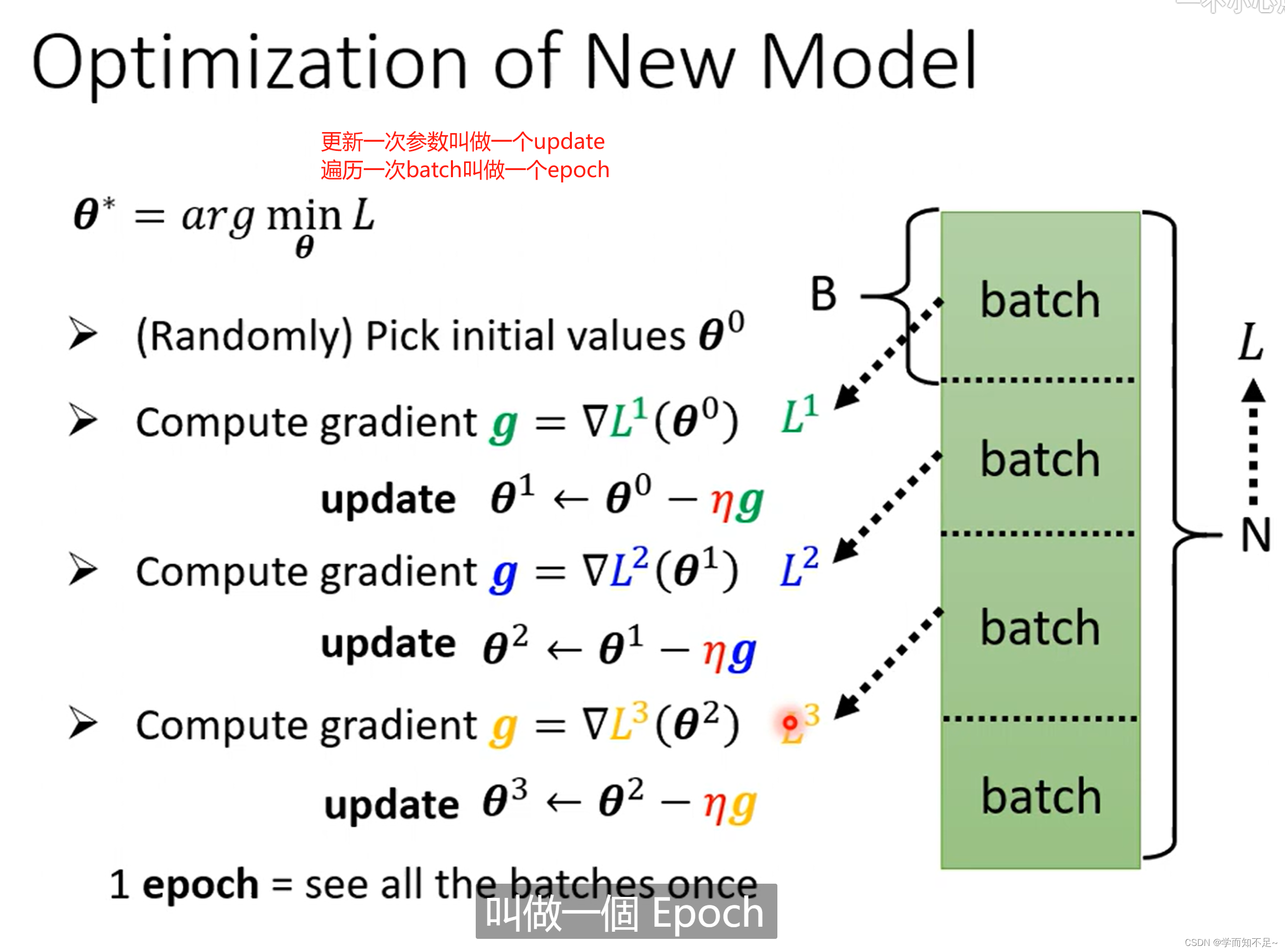
为什么要分一个个Batch?
下次课解释
数据、BatchSize、epoch、update之间的关系如下:

拓展——模型变型
模型不一定是要用sigmoid,也可以用其他的模型,比如ReLu
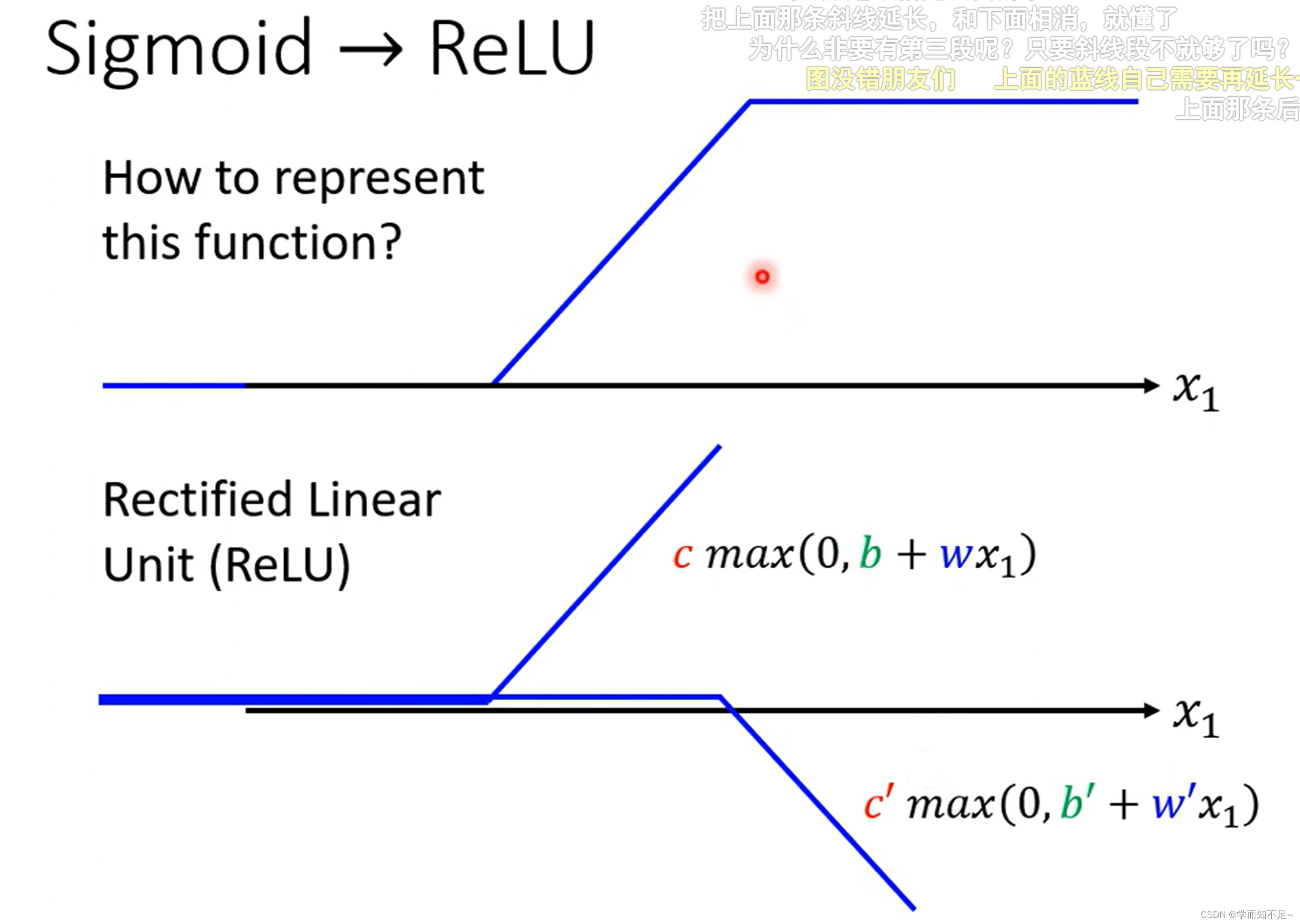

上述函数统称为激活函数(activation function)
神经网络 OR 深度学习
Neuron:神经元
Neuron Network:神经网络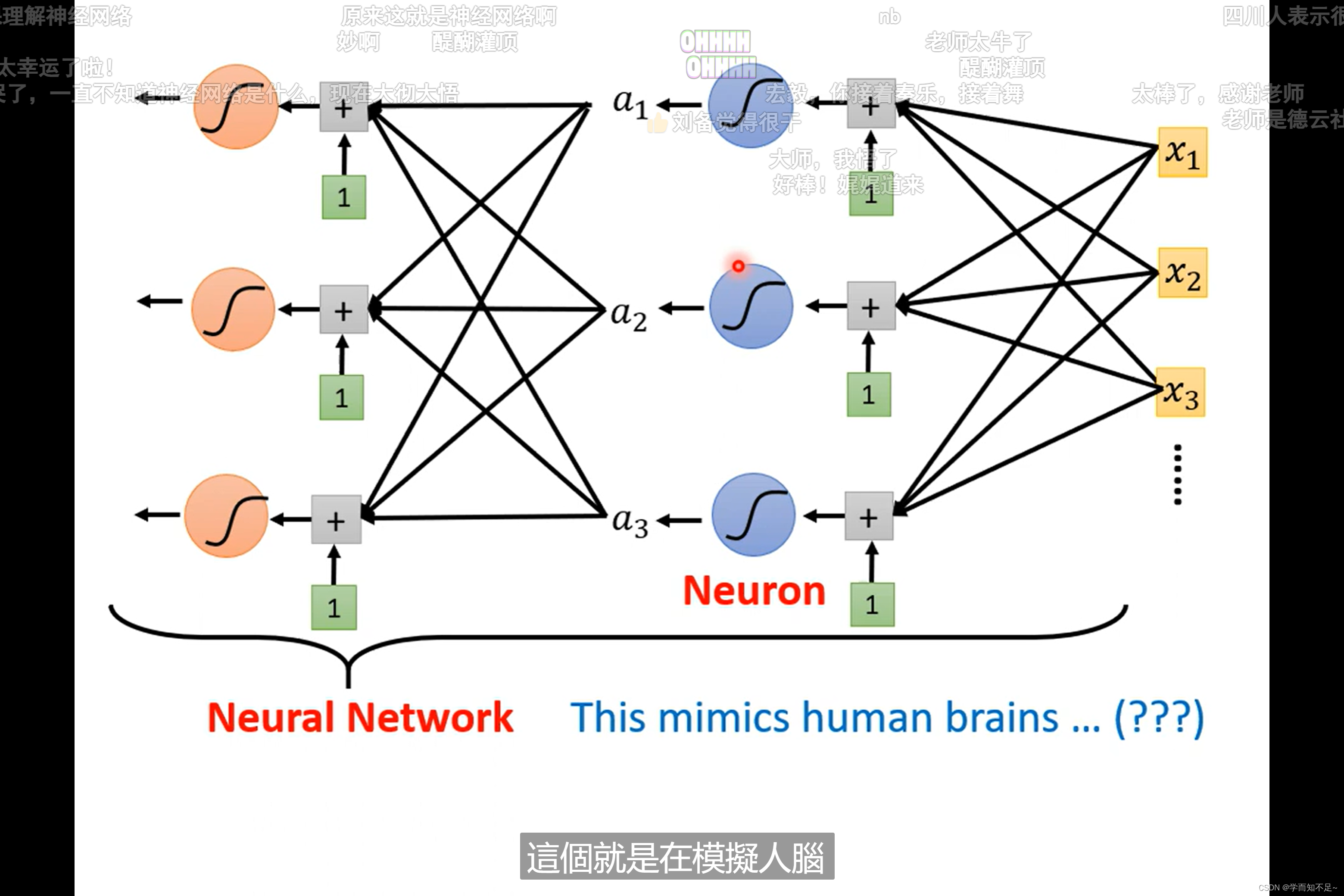
由于这个名字被搞臭了,所以换了个名字
layer:层
Deep Learning:深度学习
本质上是一个东西
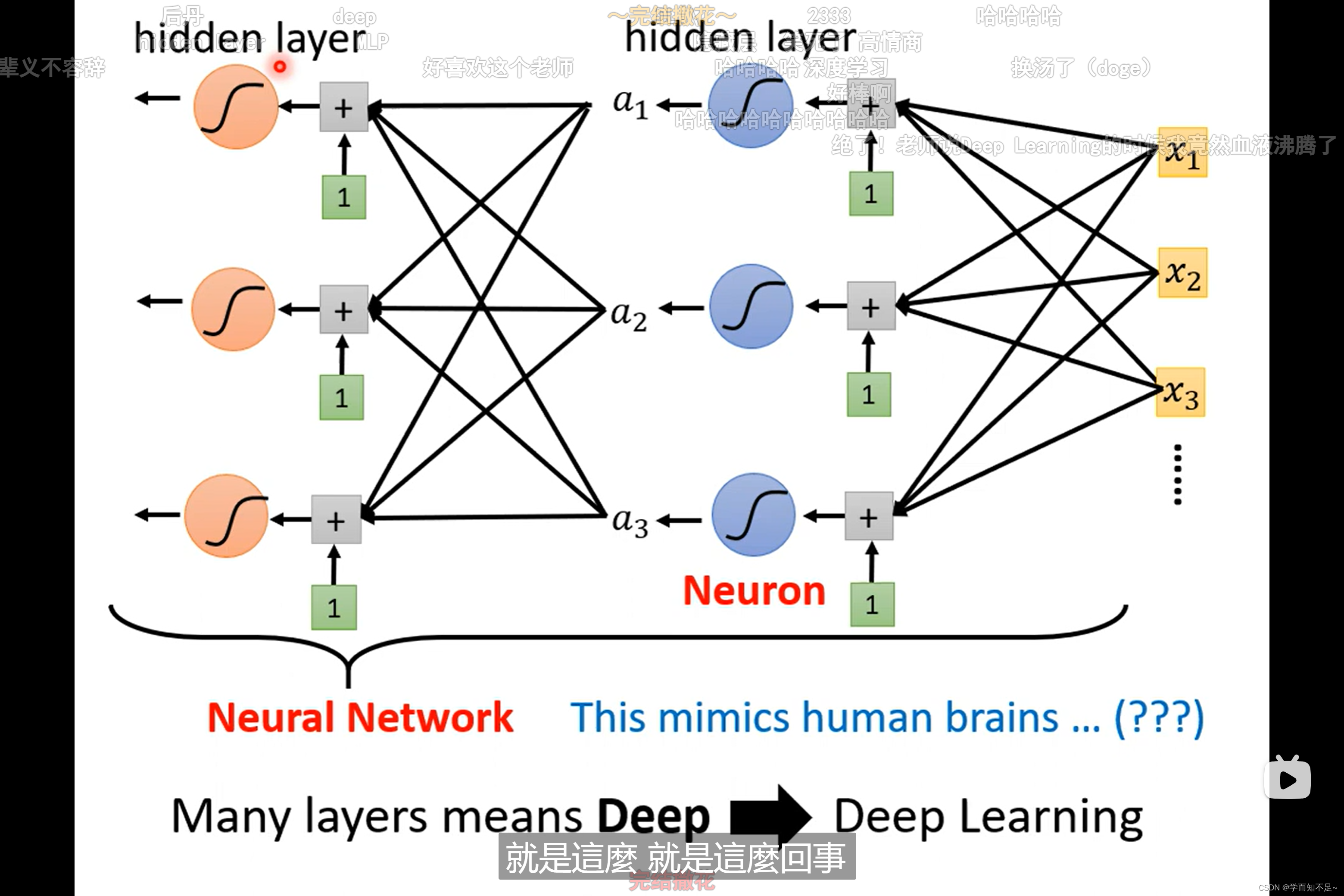
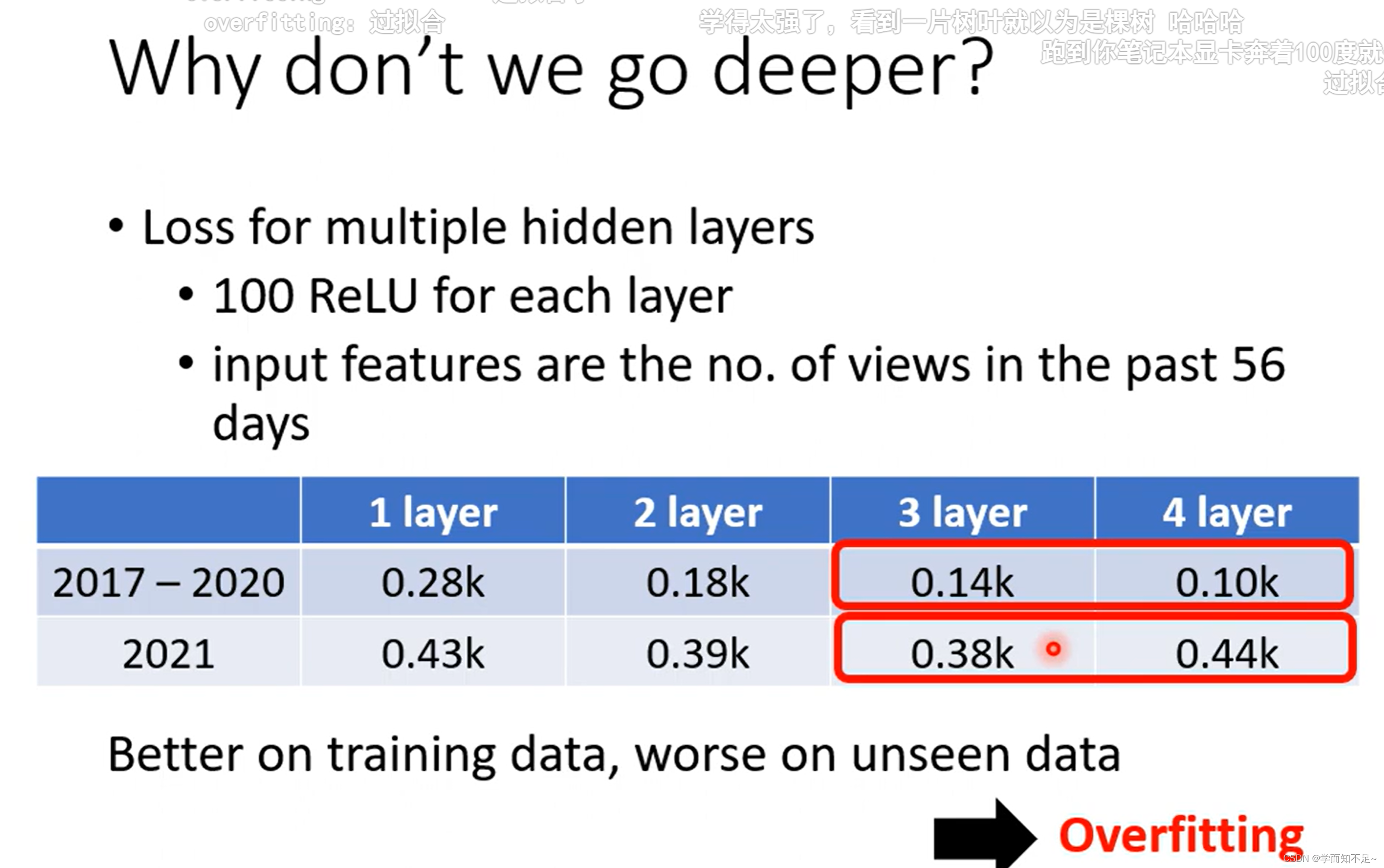
为什么不把network变胖,而是将其变深???
过拟合
over fitting