通常来说，使用消息队列主要能为我们的系统带来下面三点好处：

1. 异步处理

2. 削峰/限流

3. 降低系统耦合性

除了这三点之外，消息队列还有其他的一些应用场景，例如实现分布式事务、顺序保证和数据流处理。

异步处理

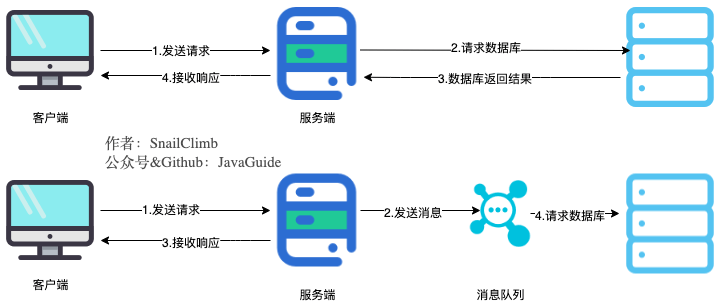
通过异步处理提高系统性能

将用户请求中包含的耗时操作，通过消息队列实现异步处理，将对应的消息发送到消息队列之后就立即返回结果，减少响应时间，提高用户体验。随后，系统再对消息进行消费。

因为用户请求数据写入消息队列之后就立即返回给用户了，但是请求数据在后续的业务校验、写数据库等操作中可能失败。因此，使用消息队列进行异步处理之后，需要适当修改业务流程进行配合，比如用户在提交订单之后，订单数据写入消息队列，不能立即返回用户订单提交成功，需要在消息队列的订单消费者进程真正处理完该订单之后，甚至出库后，再通过电子邮件或短信通知用户订单成功，以免交易纠纷。这就类似我们平时手机订火车票和电影票。

削峰/限流

先将短时间高并发产生的事务消息存储在消息队列中，然后后端服务再慢慢根据自己的能力去消费这些消息，这样就避免直接把后端服务打垮掉。

举例：在电子商务一些秒杀、促销活动中，合理使用消息队列可以有效抵御促销活动刚开始大量订单涌入对系统的冲击。如下图所示：

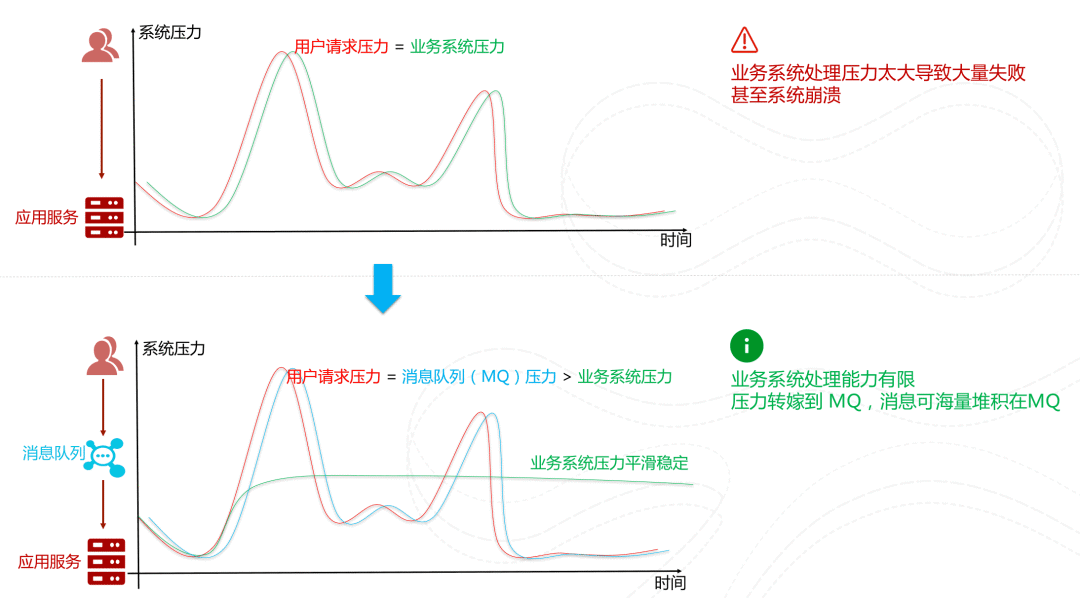
削峰

降低系统耦合性

使用消息队列还可以降低系统耦合性。我们知道如果模块之间不存在直接调用，那么新增模块或者修改模块就对其他模块影响较小，这样系统的可扩展性无疑更好一些。

生产者（客户端）发送消息到消息队列中去，消费者（服务端）处理消息，需要消费的系统直接去消息队列取消息进行消费即可而不需要和其他系统有耦合，这显然也提高了系统的扩展性。

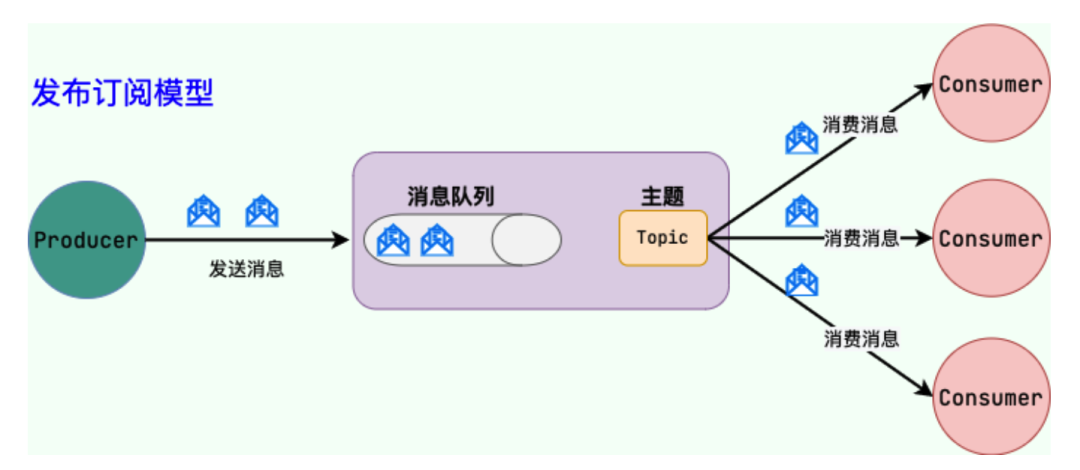
发布/订阅（Pub/Sub）模型

消息队列使用发布-订阅模式工作，消息发送者（生产者）发布消息，一个或多个消息接受者（消费者）订阅消息。 从上图可以看到消息发送者（生产者）和消息接受者（消费者）之间没有直接耦合，消息发送者将消息发送至分布式消息队列即结束对消息的处理，消息接受者从分布式消息队列获取该消息后进行后续处理，并不需要知道该消息从何而来。对新增业务，只要对该类消息感兴趣，即可订阅该消息，对原有系统和业务没有任何影响，从而实现网站业务的可扩展性设计。

例如，我们商城系统分为用户、订单、财务、仓储、消息通知、物流、风控等多个服务。用户在完成下单后，需要调用财务（扣款）、仓储（库存管理）、物流（发货）、消息通知（通知用户发货）、风控（风险评估）等服务。使用消息队列后，下单操作和后续的扣款、发货、通知等操作就解耦了，下单完成发送一个消息到消息队列，需要用到的地方去订阅这个消息进行消息即可。

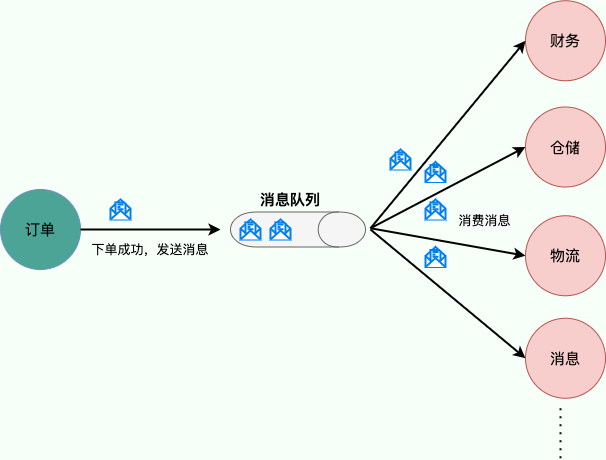
另外，为了避免消息队列服务器宕机造成消息丢失，会将成功发送到消息队列的消息存储在消息生产者服务器上，等消息真正被消费者服务器处理后才删除消息。在消息队列服务器宕机后，生产者服务器会选择分布式消息队列服务器集群中的其他服务器发布消息。

备注： 不要认为消息队列只能利用发布-订阅模式工作，只不过在解耦这个特定业务环境下是使用发布-订阅模式的。除了发布-订阅模式，还有点对点订阅模式（一个消息只有一个消费者），我们比较常用的是发布-订阅模式。另外，这两种消息模型是 JMS 提供的，AMQP 协议还提供了另外 5 种消息模型。

实现分布式事务

分布式事务的解决方案之一就是 MQ 事务。

RocketMQ、 Kafka、Pulsar、QMQ 都提供了事务相关的功能。事务允许事件流应用将消费，处理，生产消息整个过程定义为一个原子操作。

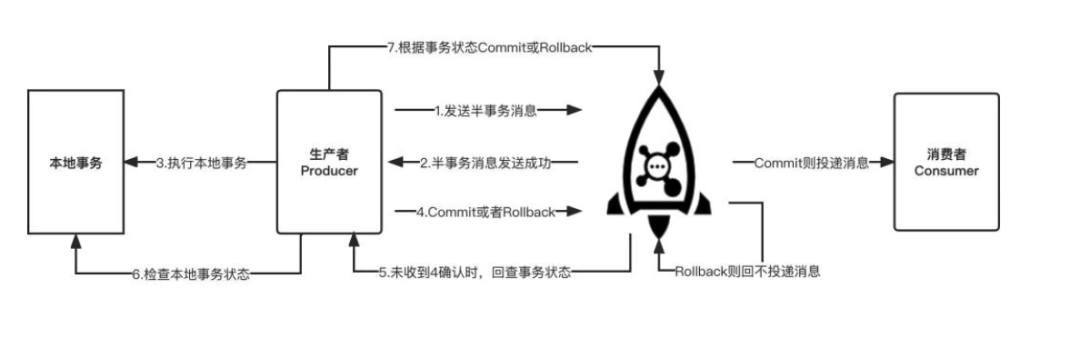
RocketMQ 事务消息原理如下图所示:

顺序保证

在很多应用场景中，处理数据的顺序至关重要。消息队列保证数据按照特定的顺序被处理，适用于那些对数据顺序有严格要求的场景。大部分消息队列，例如 RocketMQ、RabbitMQ、Pulsar、Kafka，都支持顺序消息。

延时/定时处理

消息发送后不会立即被消费，而是指定一个时间，到时间后再消费。大部分消息队列，例如 RocketMQ、RabbitMQ、Pulsar、Kafka，都支持定时/延时消息。

数据流处理

针对分布式系统产生的海量数据流，如业务日志、监控数据、用户行为等，消息队列可以实时或批量收集这些数据，并将其导入到大数据处理引擎中，实现高效的数据流管理和处理。

站在巨人的肩膀上：

面试官：消息队列的应用场景有哪些？