3 梯度下降算法

news2024/12/29 9:16:30

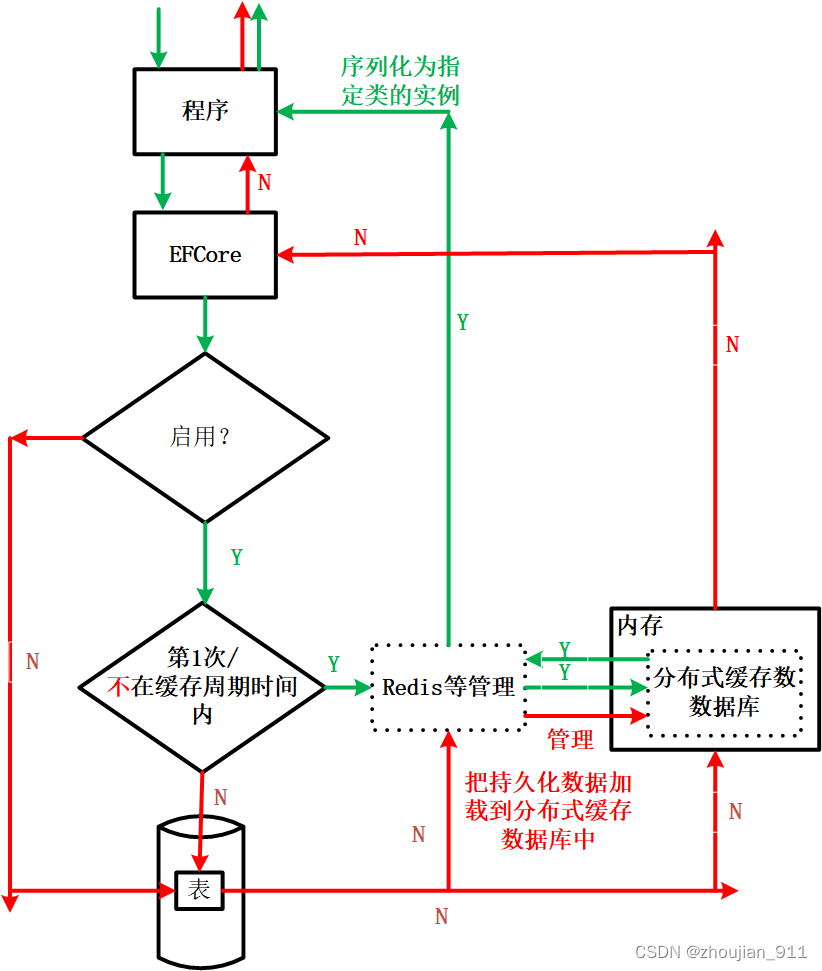
文章目录

- 问题方法
- - 穷举法
  - 分治法
- 梯度下降算法
- - 梯度
  - 梯度下降算法
- 课程代码
- - 随机梯度下降算法
  - 批量梯度下降（mini-batch）

课程来源：链接
其他觉得别人总结的比自己好，采用之的：链接
以及 BirandaのBlog！

问题方法

穷举法

在上一篇文章中，所使用的思想基于穷举，即提前已经设定好参数的准确值在某个区间内并以某个步长进行穷举（np.arange(0.0,4.1,0.1)）。

这样的思想在多维的情况下，即多个参数的时候，会引起维度诅咒的情况，在一个N维曲面中找一个最低点。使得原问题变得不可解。基于这样的问题，需要进行改进。

分治法

大化小，小化无，先对整体进行分割采样，在相对最低点进行进一步采样，直到其步长与误差符合条件。
但分治法有两个缺点：

容易只找到局部最优解，而不易找到一个全局最优解

如果需要分得更加细致，则计算量仍然巨大

由于以上问题的存在，引起了参数优化的问题，即求解使loss最小时的参数得值
$\omega ^* = \mathop{\arg\min}_\omega cost(\omega)$

梯度下降算法

梯度

梯度即导数变化最大的值，其方向为导数变化最大的方向。
$\frac{\partial f}{\partial x}=\lim_{\triangle x\rightarrow\infty}\frac{f(x+\triangle x)-f(x)}{\triangle x}$
若设 $\triangle x>0$ ,则对于增函数，梯度为上升方向，对于减函数，梯度为下降方向。如此方向都不是离极值点渐进的方向，因此需要取梯度下降的方向即梯度的反方向作为变化方向。

梯度下降算法

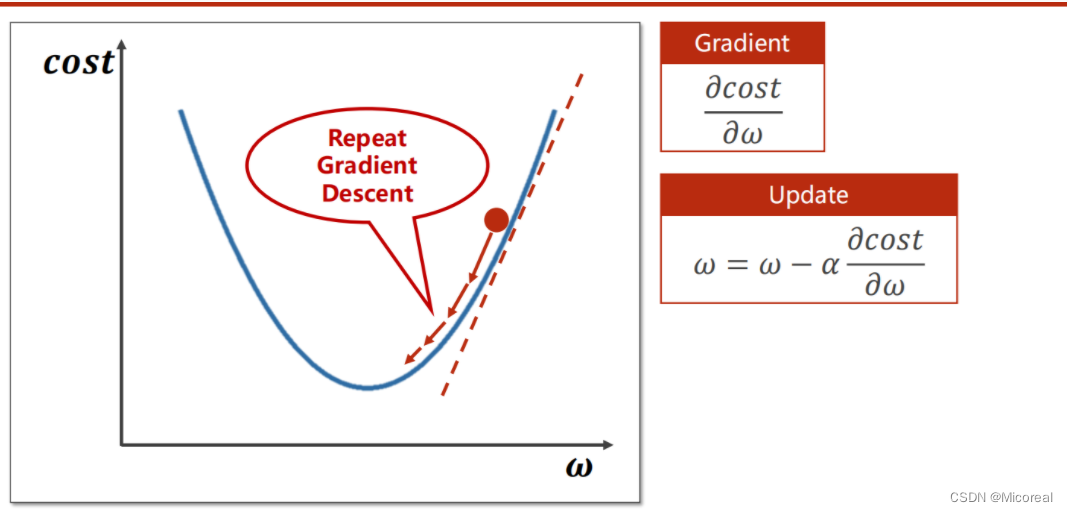
在这里插入图片描述
以凸函数为例，对于当前所选择的 $\omega$ 的值，显然并不是最低点。而对于将来要到达的全局的最低点，当前点只能向下取值，即向梯度下降方向变化。

具体的求导过程

在这里插入图片描述
即关键式子：

课程代码

梯度下降法：

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
_cost = []
w = 1.0
#前馈计算
def forward(x):
    return x * w
#求MSE
def cost(xs, ys):
    cost = 0
    for x, y in zip(xs,ys):
        y_pred = forward(x)
        cost += (y_pred-y) ** 2
    return cost/len(xs)
#求梯度
def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs,ys):
        temp = forward(x)
        grad += 2*x*(temp-y)
    return grad / len(xs)

for epoch in range(100):
     cost_val = cost(x_data, y_data)
     _cost.append(cost_val)
     grad_val = gradient(x_data, y_data)
     w -= 0.01*grad_val
     print("Epoch: ",epoch, "w = ",w ,"loss = ", cost_val)
print("Predict(after training)",4,forward(4))

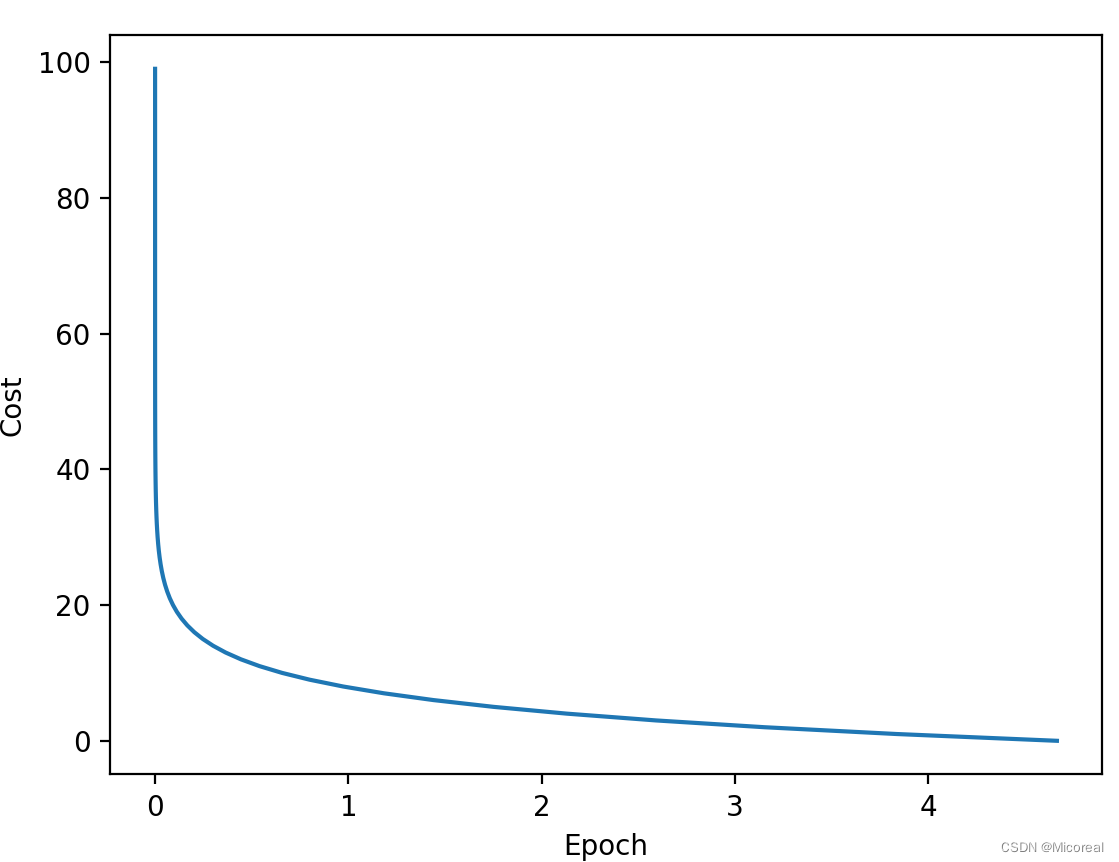
#绘图
plt.plot(_cost,range(100))
plt.ylabel("Cost")
plt.xlabel('Epoch')
plt.show()

输出结果：
在这里插入图片描述

随机梯度下降算法

随机选单个样本的损失为标准
即原公式变为
$\omega = \omega - \alpha \frac{\partial loss}{\partial \omega}$
其中
$\frac{\partial loss_n}{\partial \omega} = 2 x_n(x_n \omega - y_n)$

优点：有可能跨越鞍点（神经网络常用）

#随机梯度下降
import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
_cost = []
w = 1.0
#前馈计算
def forward(x):
    return x * w
#求单个loss
def loss(x, y):
    y_pred = forward(x)
    return (y_pred-y) ** 2
#求梯度
def gradient(x, y):
    return 2*x*(x*w-y)
print("Predict(after training)",4,forward(4))

for epoch in range(100):
    for x, y in zip(x_data,y_data):
        grad=gradient(x,y) 
        w -= 0.01*grad
        print("\tgrad:  ",x,y,grad)
        l = loss(x,y)
    print("progress: ",epoch,"w=",w,"loss=",l)
print("Predict(after training)",4,forward(4))