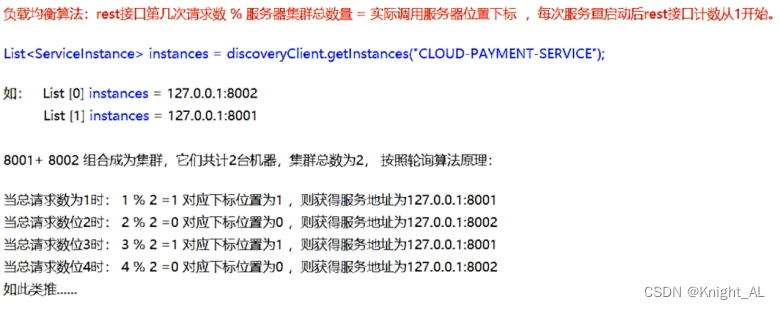
连载文章,长期更新,欢迎关注:
同前面介绍过的大多数算法一样,RTABMAP也采用基于优化的方法来求解SLAM问题,系统框架同样遵循前端里程计、后端优化和闭环检测的三段式范式。这里重点讨论RTABMAP两大亮点,一个亮点是支持视觉和激光融合,另一个亮点是内存管理机制。下面将从原理分析、源码解读和安装与运行这3个方面展开讲解RTABMAP算法。
10.1.1 RTABMAP原理分析
经过前面章节的学习,相信大家对一些具体的SLAM框架实现过程已经不陌生了。因此在正式介绍RTABMAP的原理之前,先来看一下RTABMAP与其他一些SLAM框架的异同之处,如图10-1所示。比较维度主要在输入(Inputs)和输出(Online Outputs),常见的输入包括双目相机(Stereo)、RGB-D、多相机(Multi)、IMU、单线雷达(2D Lidar)、多线雷达(3D Lidar)和里程计(Odom),而输出包括位姿(Pose)、二维占据地图(2D Occupancy)、三维占据地图(3D Occupancy)和点云地图(Point Cloud)。同前面已经介绍过的Gmapping、Cartographer、ORB-SLAM2等相比可以说RTABMAP的表现近乎完美,RTABMAP的输入支持视觉(Stereo、RGB-D、Multi)、激光(2D Lidar、3D Lidar)和里程计(Odom),而输出则支持位姿(Pose)、二维占据地图(2D Occupancy)、三维占据地图(3D Occupancy)和点云地图(Point Cloud)。激光传感器的优点是可以直接感知环境障碍物信息并生成可以用于机器人自主导航的二维占据地图(2D Occupancy)或三维占据地图(3D Occupancy),这也是为什么大多数能够进行自主导航的机器人用的都是激光SLAM。视觉传感器的优点是感知到的信息量大,定位过程的位姿(Pose)不易丢失。当然像Stereo和RGB-D这样能直接感知深度信息的视觉传感器,如果最终构建出来的是稠密点云地图(Dense Point Cloud),那么也可以将稠密点云地图转换成二维占据地图(2D Occupancy)或三维占据地图(3D Occupancy)后用于机器人自主导航。而里程计(Odom)一般由安装在车轮上的编码器提供(这种情况也叫轮式里程计),里程计能提供短期运动信息在局部建图过程为位姿估计提供预测信息,当环境特征缺失时里程计也能提供短期位姿估计。
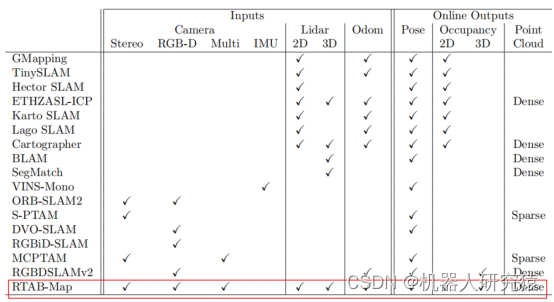
图10-1 RTABMAP与其他框架比较
1.RTABMAP系统框架
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
2.内存管理机制(STM、WM和LTM)
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
3.里程计节点(Odometry Node)
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
4.局部地图
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
5.闭环检测与图优化
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
6.全局地图
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
10.1.2 RTABMAP源码解读
上面讨论完RTABMAP的原理,现在就来解读RTABMAP的源码,其代码框架如图10-14所示。与前面已经分析过的算法类似,RTABMAP的代码由接口部分和核心库部分组成。rtabmap_ros功能包实现了算法的ROS接口,其中的主节点rtabmap负责启动算法主逻辑,而算法的底层具体实现被封装在rtabmap核心库之中。
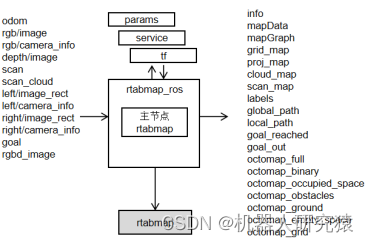
图10-14 RTABMAP代码框架
1.rtabmap_ros功能包
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
2.rtabmap核心库
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
10.1.3 RTABMAP安装与运行
学习完RTABMAP算法的原理及源码之后,大家肯定迫不及待想亲自安装运行一下RTABMAP体验一下真实效果。庆幸的是,rtabmap核心库的ROS版本已支持到 noetic,而rtabmap_ros的ROS版本已支持到ros2,可以说是版本更新最及时的一个SLAM框架了。在第1章中已经声明过,本书在Ubuntu18.04和ROS melodic环境下进行讨论,所以下面就以ROS melodic版本的rtabmap和rtabmap_ros为例进行安装和运行。
1.RTABMAP安装
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
2.RTABMAP离线运行
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
3.RTABMAP在线运行
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
参考文献
【1】 张虎,机器人SLAM导航核心技术与实战[M]. 机械工业出版社,2022.