● 由多元函数全部变量的偏导数汇总而成的向量称为梯度(gradient)。梯度指示的方向是各点处的函数值减小最多的方向。
● 虽然梯度的方向并不一定指向最小值,但沿着它的方向能够最大限度地减小函数的值。因此,在寻找函数的最小值(或者尽可能小的值)的位置的任务中,要以梯度的信息为线索,决定前进的方向。
● 此时梯度法就派上用场了。在梯度法中,函数的取值从当前位置沿着梯度方向前进一定距离,然后在新的地方重新求梯度,再沿着新梯度方向前进,如此反复,不断地沿梯度方向前进。像这样,通过不断地沿梯度方向前进,逐渐减小函数值的过程就是梯度法(gradient method)。梯度法是解决机器学习中最优化问题的常用方法,特别是在神经网络的学习中经常被使用。
下文给出了利用梯度法求函数 的最小值的 Python 代码。
【梯度法求函数最小值的Python代码】
import numpy as np
import matplotlib.pylab as plt
def numerical_gradient_no_batch(f,x):
h=1e-4
grad=np.zeros_like(x)
for idx in range(x.size):
tmp_val=x[idx]
x[idx]=float(tmp_val)+h
fxh1=f(x)
x[idx]=tmp_val-h
fxh2=f(x)
grad[idx]=(fxh1-fxh2)/(2*h)
x[idx]=tmp_val
return grad
def numerical_gradient(f,X):
if X.ndim==1:
return numerical_gradient_no_batch(f,X)
else:
grad=np.zeros_like(X)
for idx,x in enumerate(X):
grad[idx]=numerical_gradient_no_batch(f,x)
return grad
def gradient_descent(f,init_x,lr=0.01,step_num=100):
x=init_x
x_history=[]
for i in range(step_num):
x_history.append( x.copy() )
grad=numerical_gradient(f,x)
x-=lr*grad
return x,np.array(x_history)
def function_2(x):
return x[0]**2+x[1]**2
init_x=np.array([-3.0,4.0])
lr=0.1
step_num=20
x,x_history=gradient_descent(function_2,init_x,lr=lr,step_num=step_num)
plt.plot( [-5,5],[0,0],'--b')
plt.plot( [0,0],[-5,5],'--b')
plt.plot(x_history[:,0],x_history[:,1],'o')
plt.xlim(-3.5,3.5)
plt.ylim(-4.5,4.5)
plt.xlabel("X0")
plt.ylabel("X1")
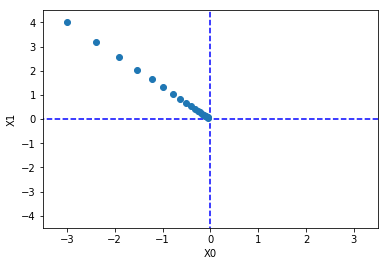
plt.show()【程序运行结果】
运行上面代码后,可输出如下图像。
若输入命令:
gradient_descent(function_2,init_x=init_x,lr=0.1,step_num=100)可得如下输出结果:
(array([-7.04562775e-12, 9.39417033e-12]),
array([[-3.45876451e-02, 4.61168602e-02],
[-2.76701161e-02, 3.68934881e-02],
[-2.21360929e-02, 2.95147905e-02],
[-1.77088743e-02, 2.36118324e-02],
[-1.41670994e-02, 1.88894659e-02],
[-1.13336796e-02, 1.51115727e-02],
[-9.06694365e-03, 1.20892582e-02],
[-7.25355492e-03, 9.67140656e-03],
[-5.80284393e-03, 7.73712525e-03],
[-4.64227515e-03, 6.18970020e-03],
[-3.71382012e-03, 4.95176016e-03],
[-2.97105609e-03, 3.96140813e-03],
[-2.37684488e-03, 3.16912650e-03],
[-1.90147590e-03, 2.53530120e-03],
[-1.52118072e-03, 2.02824096e-03],
[-1.21694458e-03, 1.62259277e-03],
[-9.73555661e-04, 1.29807421e-03],
[-7.78844529e-04, 1.03845937e-03],
[-6.23075623e-04, 8.30767497e-04],
[-4.98460498e-04, 6.64613998e-04],
[-3.98768399e-04, 5.31691198e-04],
[-3.19014719e-04, 4.25352959e-04],
[-2.55211775e-04, 3.40282367e-04],
[-2.04169420e-04, 2.72225894e-04],
[-1.63335536e-04, 2.17780715e-04],
[-1.30668429e-04, 1.74224572e-04],
[-1.04534743e-04, 1.39379657e-04],
[-8.36277945e-05, 1.11503726e-04],
[-6.69022356e-05, 8.92029808e-05],
[-5.35217885e-05, 7.13623846e-05],
[-4.28174308e-05, 5.70899077e-05],
[-3.42539446e-05, 4.56719262e-05],
[-2.74031557e-05, 3.65375409e-05],
[-2.19225246e-05, 2.92300327e-05],
[-1.75380196e-05, 2.33840262e-05],
[-1.40304157e-05, 1.87072210e-05],
[-1.12243326e-05, 1.49657768e-05],
[-8.97946606e-06, 1.19726214e-05],
[-7.18357285e-06, 9.57809713e-06],
[-5.74685828e-06, 7.66247770e-06],
[-4.59748662e-06, 6.12998216e-06],
[-3.67798930e-06, 4.90398573e-06],
[-2.94239144e-06, 3.92318858e-06],
[-2.35391315e-06, 3.13855087e-06],
[-1.88313052e-06, 2.51084069e-06],
[-1.50650442e-06, 2.00867256e-06],
[-1.20520353e-06, 1.60693804e-06],
[-9.64162827e-07, 1.28555044e-06],
[-7.71330261e-07, 1.02844035e-06],
[-6.17064209e-07, 8.22752279e-07],
[-4.93651367e-07, 6.58201823e-07],
[-3.94921094e-07, 5.26561458e-07],
[-3.15936875e-07, 4.21249167e-07],
[-2.52749500e-07, 3.36999333e-07],
[-2.02199600e-07, 2.69599467e-07],
[-1.61759680e-07, 2.15679573e-07],
[-1.29407744e-07, 1.72543659e-07],
[-1.03526195e-07, 1.38034927e-07],
[-8.28209562e-08, 1.10427942e-07],
[-6.62567649e-08, 8.83423532e-08],
[-5.30054119e-08, 7.06738826e-08],
[-4.24043296e-08, 5.65391061e-08],
[-3.39234636e-08, 4.52312849e-08],
[-2.71387709e-08, 3.61850279e-08],
[-2.17110167e-08, 2.89480223e-08],
[-1.73688134e-08, 2.31584178e-08],
[-1.38950507e-08, 1.85267343e-08],
[-1.11160406e-08, 1.48213874e-08],
[-8.89283245e-09, 1.18571099e-08],
[-7.11426596e-09, 9.48568795e-09],
[-5.69141277e-09, 7.58855036e-09],
[-4.55313022e-09, 6.07084029e-09],
[-3.64250417e-09, 4.85667223e-09],
[-2.91400334e-09, 3.88533778e-09],
[-2.33120267e-09, 3.10827023e-09],
[-1.86496214e-09, 2.48661618e-09],
[-1.49196971e-09, 1.98929295e-09],
[-1.19357577e-09, 1.59143436e-09],
[-9.54860614e-10, 1.27314749e-09],
[-7.63888491e-10, 1.01851799e-09],
[-6.11110793e-10, 8.14814391e-10],
[-4.88888634e-10, 6.51851512e-10],
[-3.91110907e-10, 5.21481210e-10],
[-3.12888726e-10, 4.17184968e-10],
[-2.50310981e-10, 3.33747974e-10],
[-2.00248785e-10, 2.66998379e-10],
[-1.60199028e-10, 2.13598704e-10],
[-1.28159222e-10, 1.70878963e-10],
[-1.02527378e-10, 1.36703170e-10],
[-8.20219022e-11, 1.09362536e-10],
[-6.56175217e-11, 8.74900290e-11],
[-5.24940174e-11, 6.99920232e-11],
[-4.19952139e-11, 5.59936186e-11],
[-3.35961711e-11, 4.47948948e-11],
[-2.68769369e-11, 3.58359159e-11],
[-2.15015495e-11, 2.86687327e-11],
[-1.72012396e-11, 2.29349862e-11],
[-1.37609917e-11, 1.83479889e-11],
[-1.10087934e-11, 1.46783911e-11],
[-8.80703469e-12, 1.17427129e-11]]))
【参考文献】
https://www.cnblogs.com/thisyan/p/9715593.html