【排序算法】 冒泡排序 | 快速排序 | 归并排序

1. 冒泡排序

1.1 核心思想

将整个数组的排序问题，转化成“查找当前数组最大元素”的问题

• 比较数组中相邻元素的大小，调整顺序，保证较大的元素在较小元素后面；
• 重复上一步的比较，直到当前数组的最后一位停止；
• 已找出的最大元素不参与下一轮比较，继续重复上述两个步骤，直到不再发生交换；

以nums = [49,38,65,97,76,13,27]为例，下面看看每一轮比较的结果：

1）第一轮比较

nums[0]与nums[1]比较，需要交换顺序；

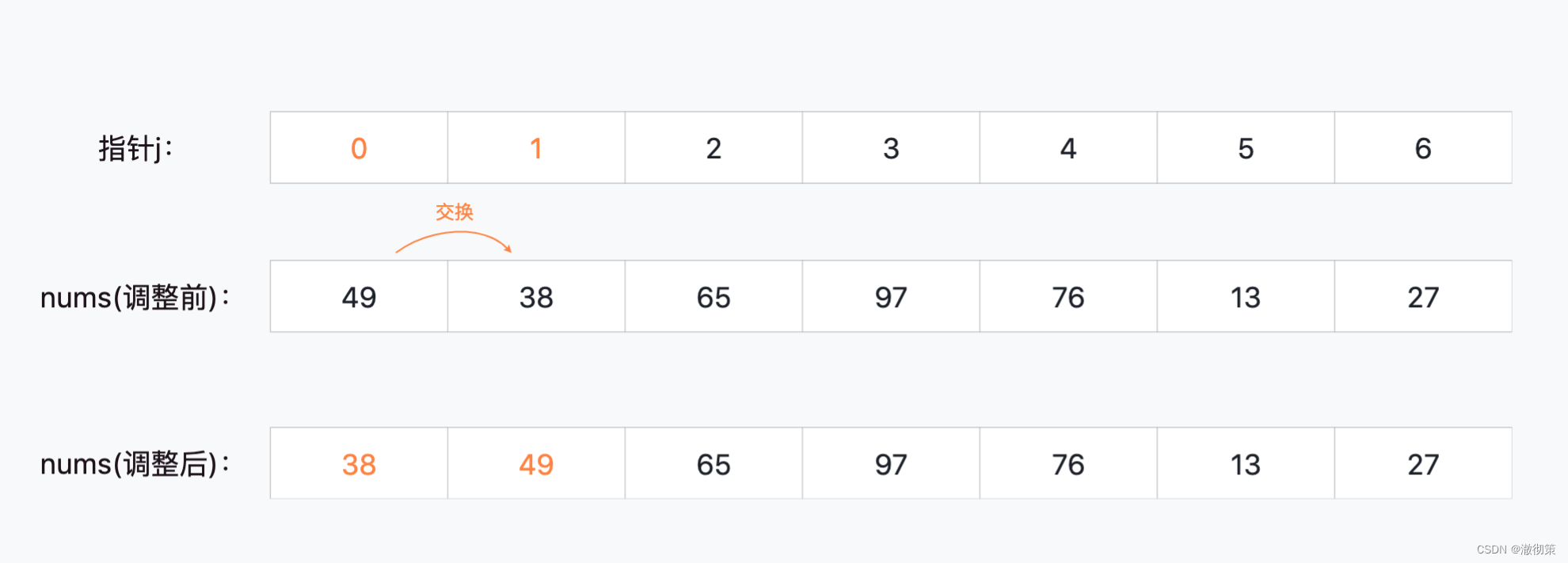
nums[1]和nums[2]比较，不变；

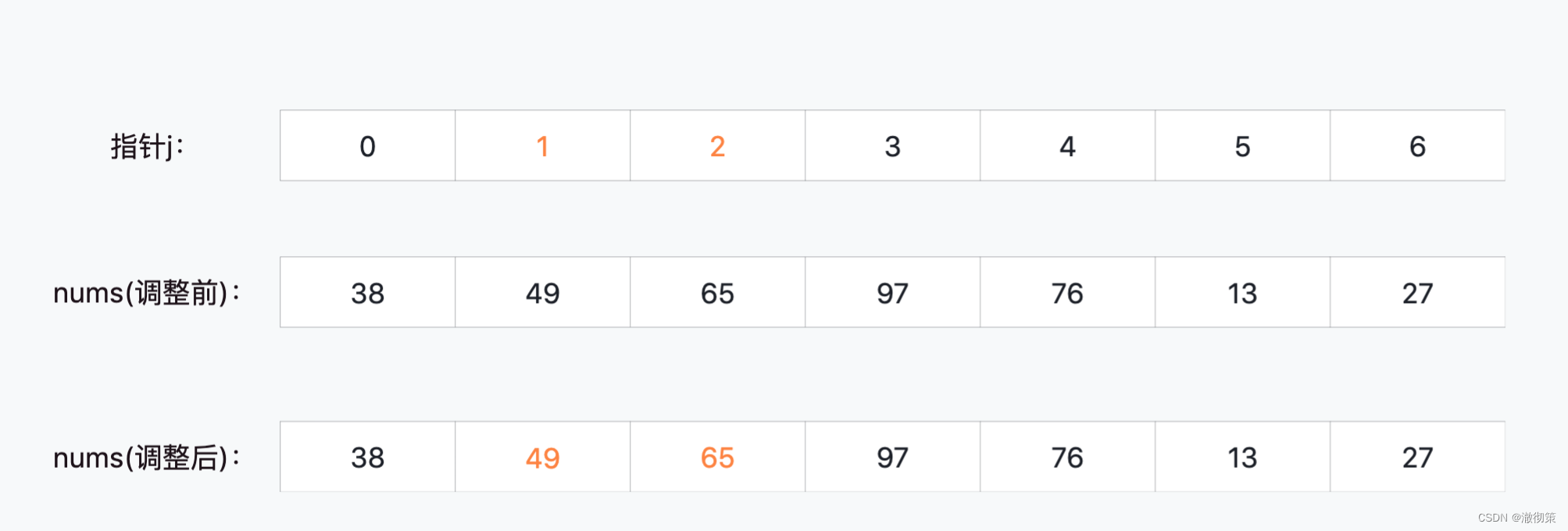
nums[2]和nums[3]比较，不变；

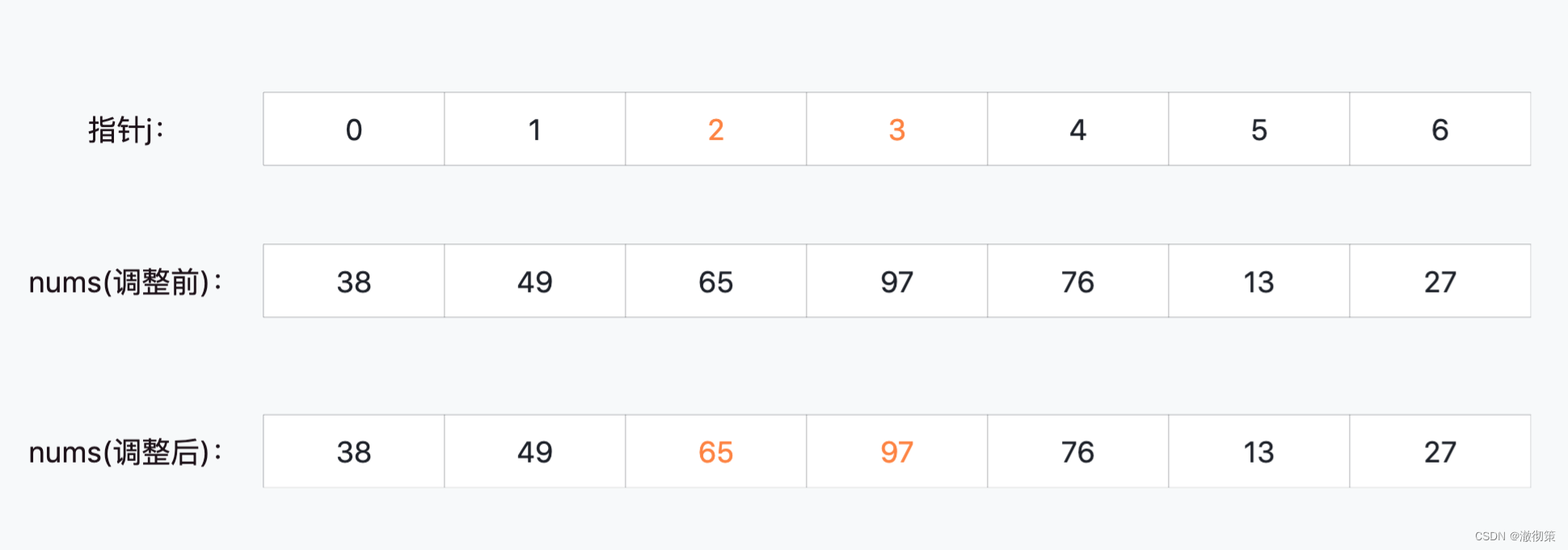
nums[3]和nums[4]比较，交换顺序；

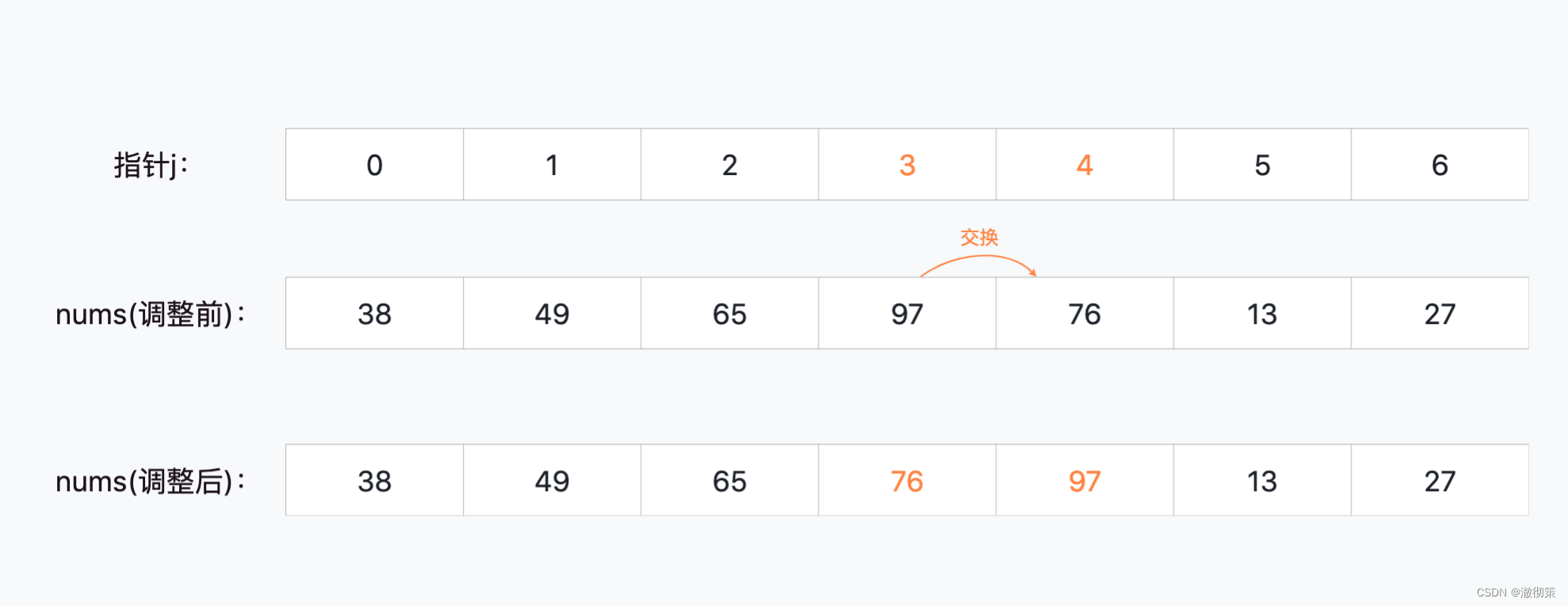
nums[4]和nums[5]比较，交换顺序；

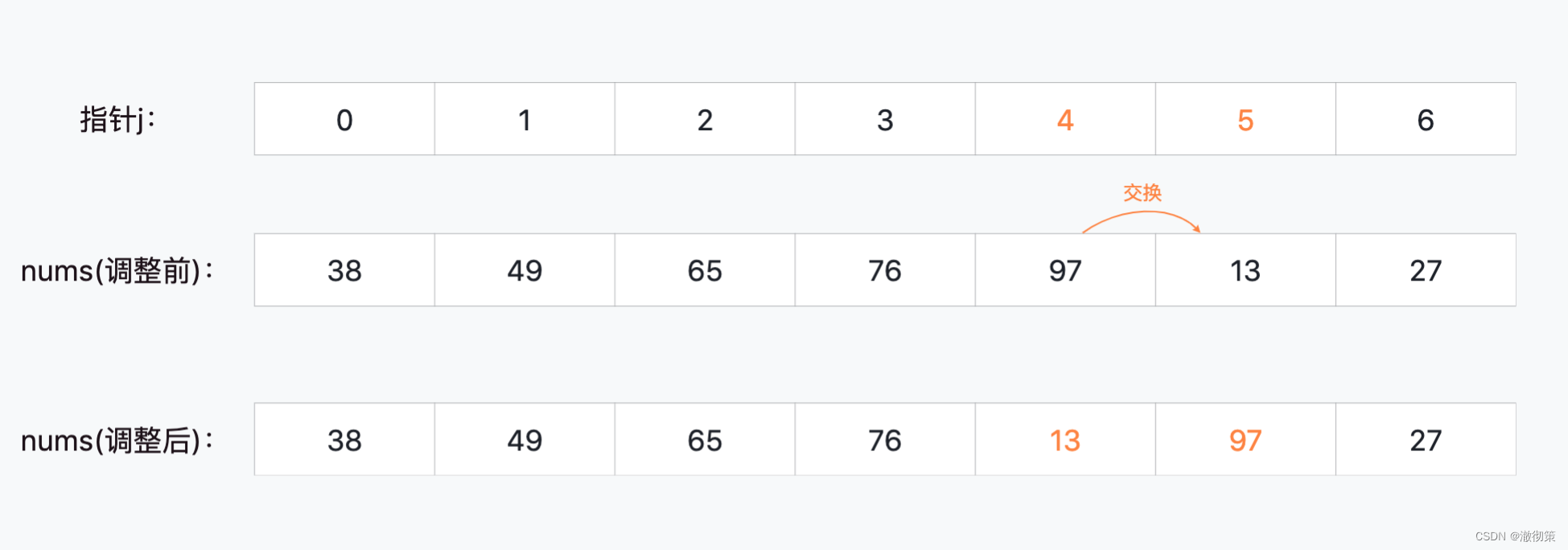
nums[5]和nums[6]比较，交换顺序，此时的元素97就是当前数组中最大的元素；

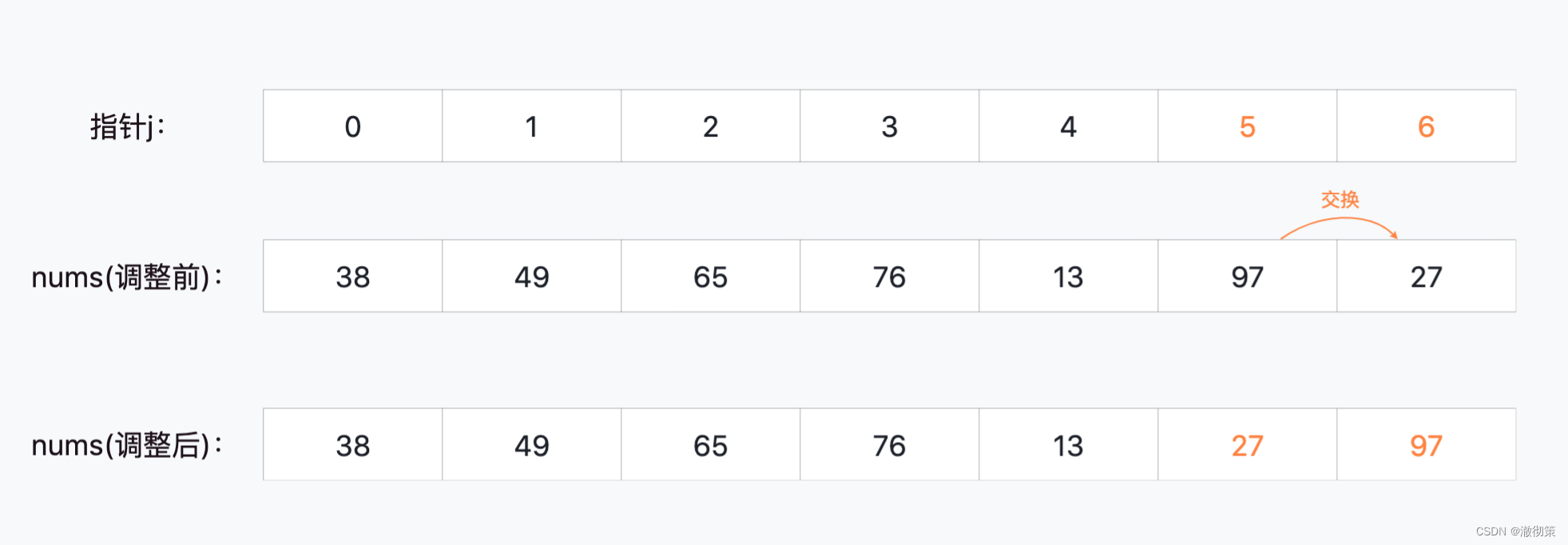
2）第二轮比较

直接看最后一轮的比较结果，nums[4]和nums[5]；

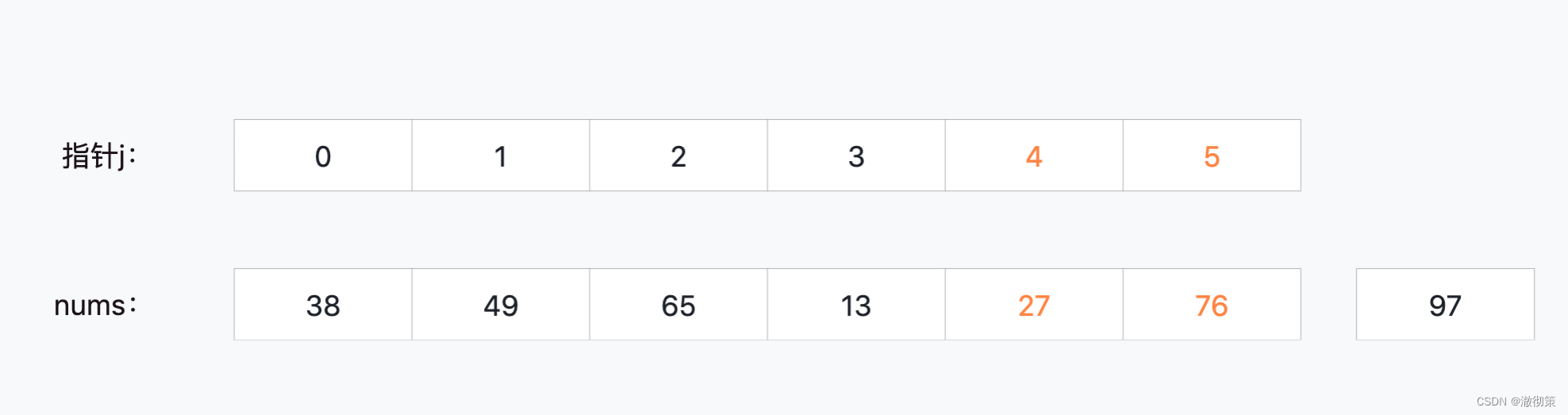
3）第三轮比较

直接看最后一轮的比较结果，nums[3]和nums[4]；

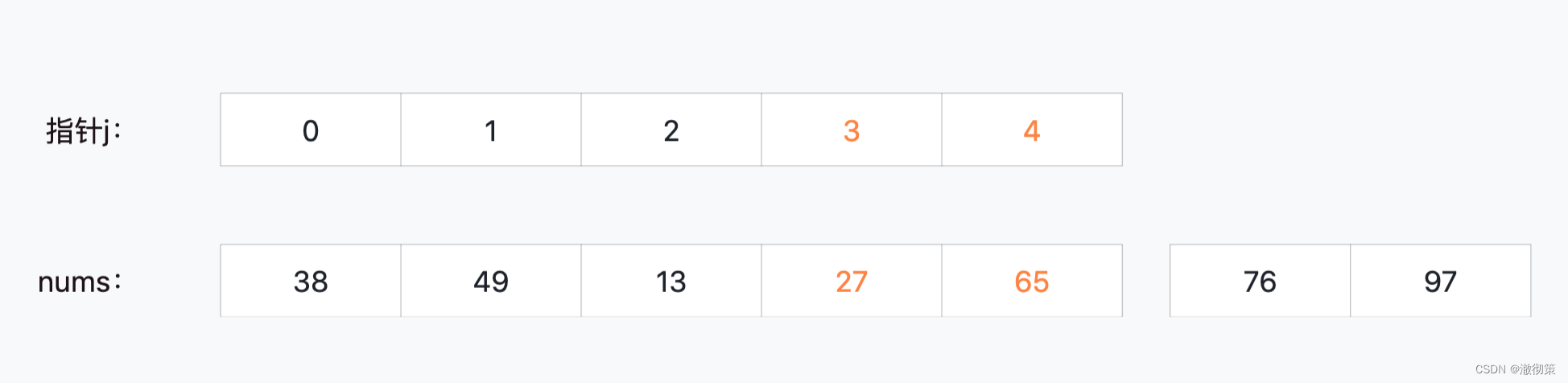
4）第四轮比较

直接看最后一轮的比较结果，nums[2]和nums[3]；

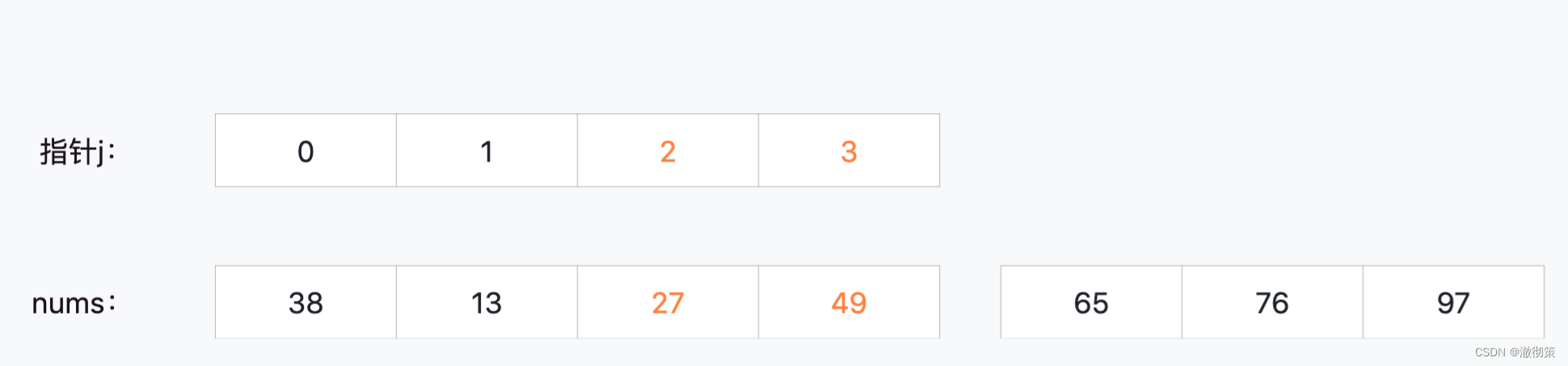
5）第五轮比较

直接看最后一轮的比较结果，nums[1]和nums[2]；

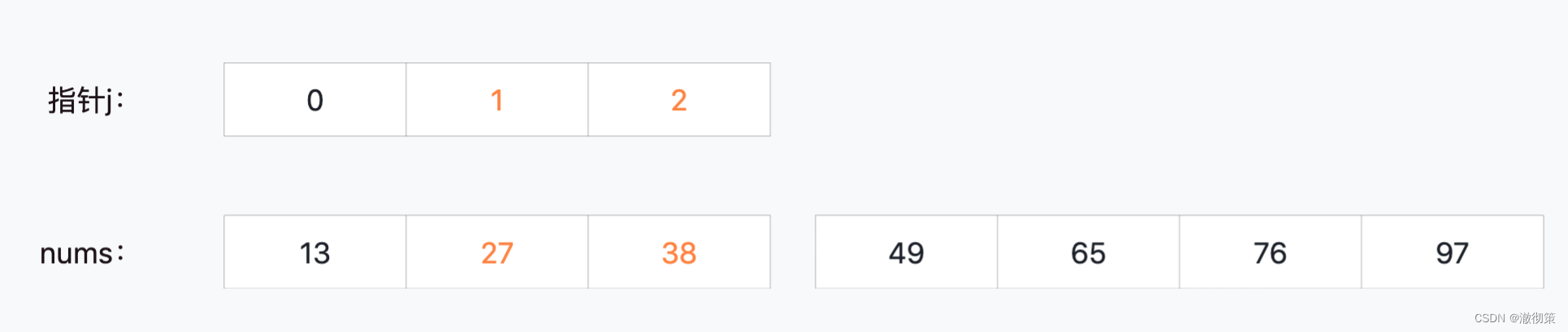
6）第六轮比较

此时当前数组只剩两个元素，nums[0]和nums[1]，比较过程中，没有发生元素交换，因此可以判定数组已经全部排序完成；

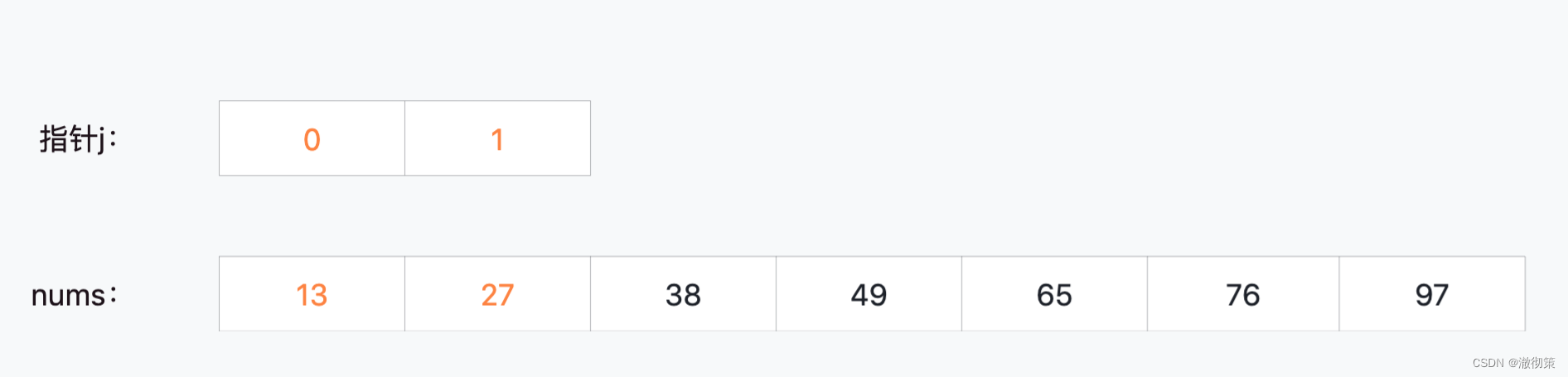
基于上述过程可以看出，我们除了要控制比较的轮次之外，还需要在每次比较中去遍历当前的子数组，对相邻元素进行比较，才能找到当前子数组中最大的元素。因此冒泡排序的时间复杂度是O(n^2)

1.2 代码实现

	public int[] sortArray(int[] nums) {
		// 比较的轮次
  	for (int i=0; i<nums.length; i++) {	
			// 相邻元素比较，较大元素后移
			boolean falg = false; // 当前比较轮次中是否发生了元素间的交换
  		for(int j=0; j< nums.length - i - 1; j++) {	
  			if(nums[j] > nums[j+1]) {
  				int tmp = nums[j];
  				nums[j] = nums[j+1];
  				nums[j+1] = tmp;
					flag = true;
  			}
  		}
			// 当前比较的轮次未发生元素交换，则代表数组已经全部排序完毕，可直接返回
			if(!flag){
				return nums;
			}
  	}
  	return nums;
  }

2. 快速排序

2.1 核心思想

将数组的排序问题，转化为“数组区间划分”问题：

• 选中的数组nums中的元素num作为基准元素；
• 重新划分当前数组的区间，使得num左边的所有元素（如果有）都小于num，num右边的所有元素（如果有）都大于num；
• 递归地在nums的左右区间（如果有）中，重复上面两个步骤，直到区间只有一个元素时停止；

以nums = [49,38,65,97,76,13,27]为例，我们选取的元素num = nums[0] = 49，为了方便划分区间，同时为左右分区各设置了一个指针i和j，i的起始下标是0，j的起始下标是6；下面看看每一轮数组划分的结果：

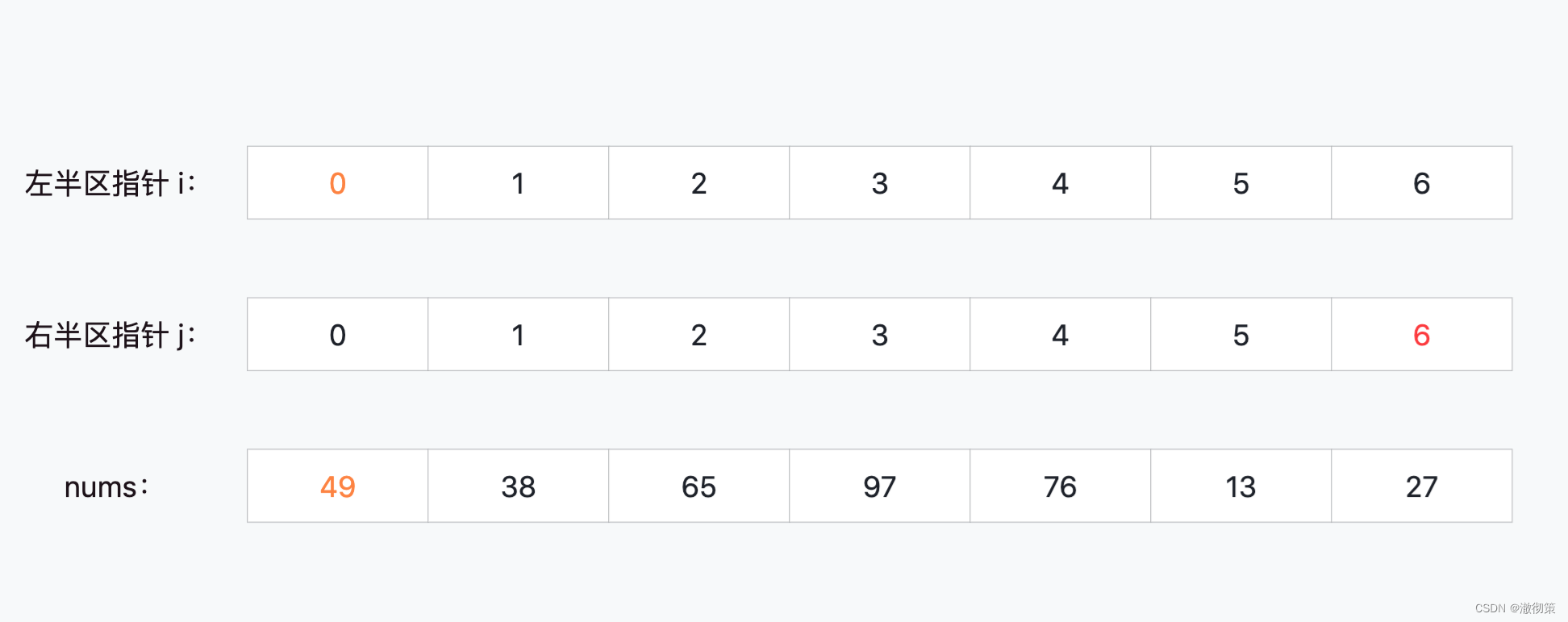
1）第一轮区间划分（选中数组第一个元素49）

当i=0, j=6时，nums[6] < 49，nums[0] = 49，nums[6]应该划分到49的左边区间；

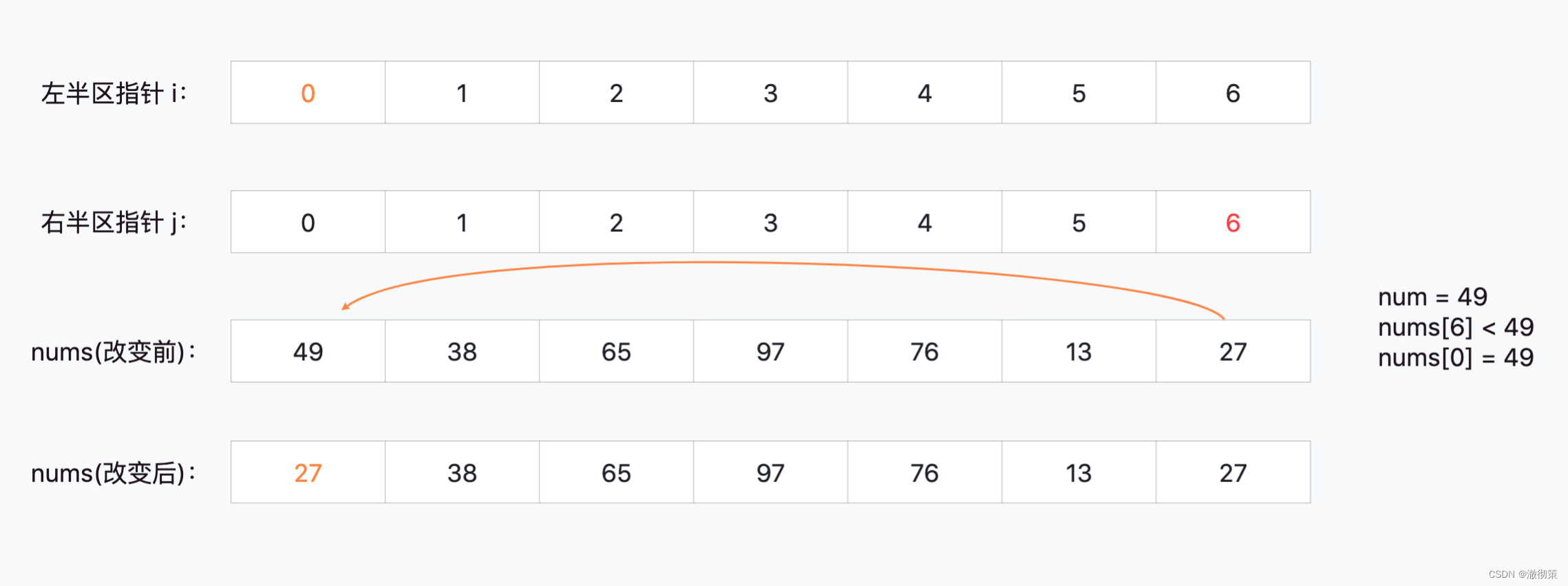
当i=1, j=6时，nums[1] < 49，符合预期，此时不做调整；

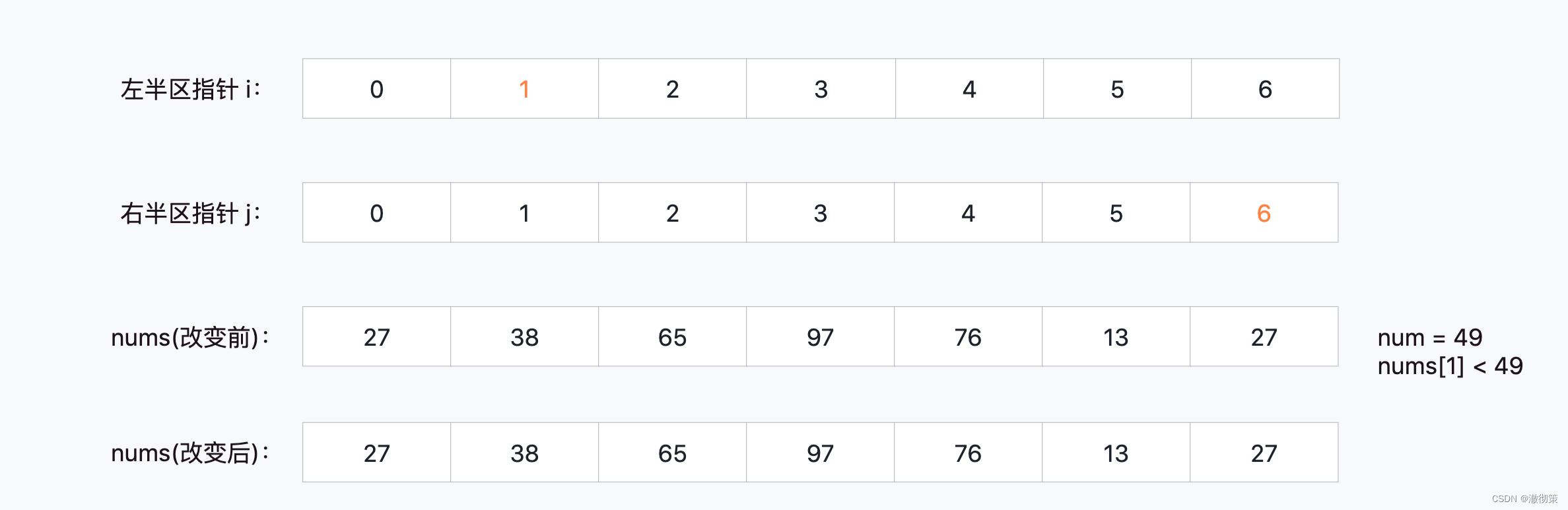
当i=2, j=6时，nums[2] > 49，nums[i]应该划分到49的右边区间；

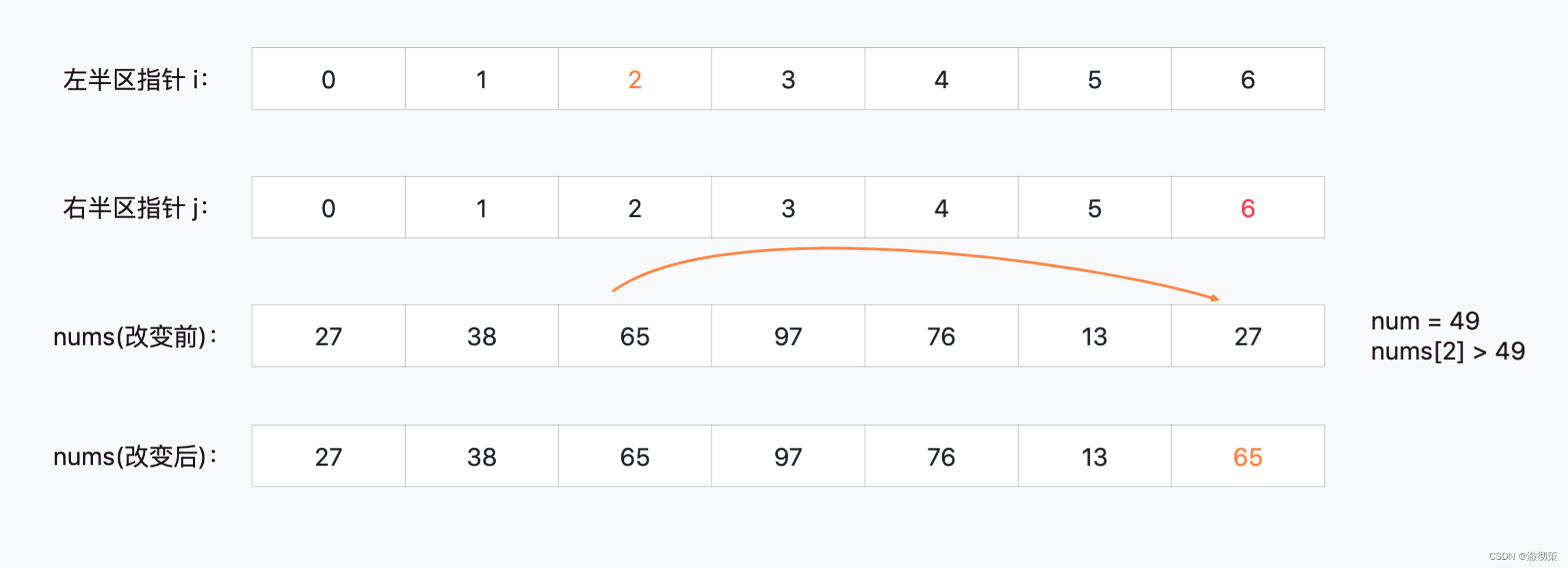
当i=2, j=5时，nums[2] > 49，nums[i]应该划分到49的右边区间；

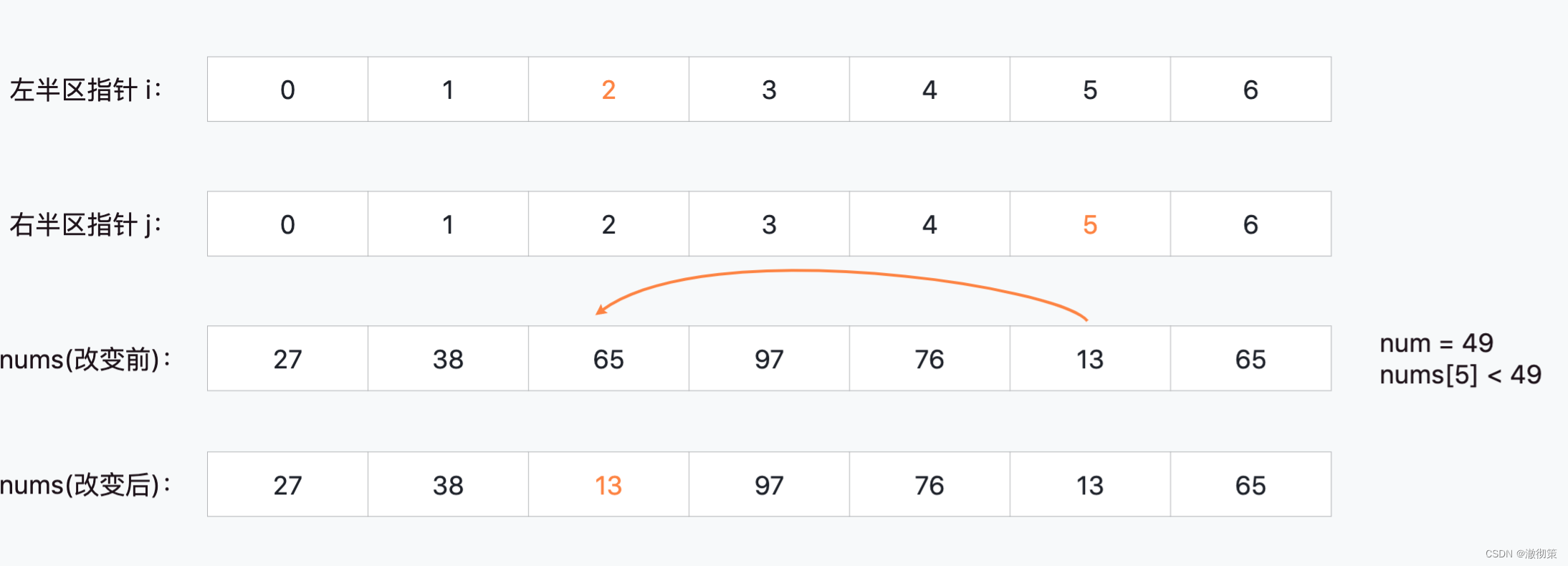
当i=3, j=5时，nums[3] > 49，nums[3]应该划分到49的右边区间；

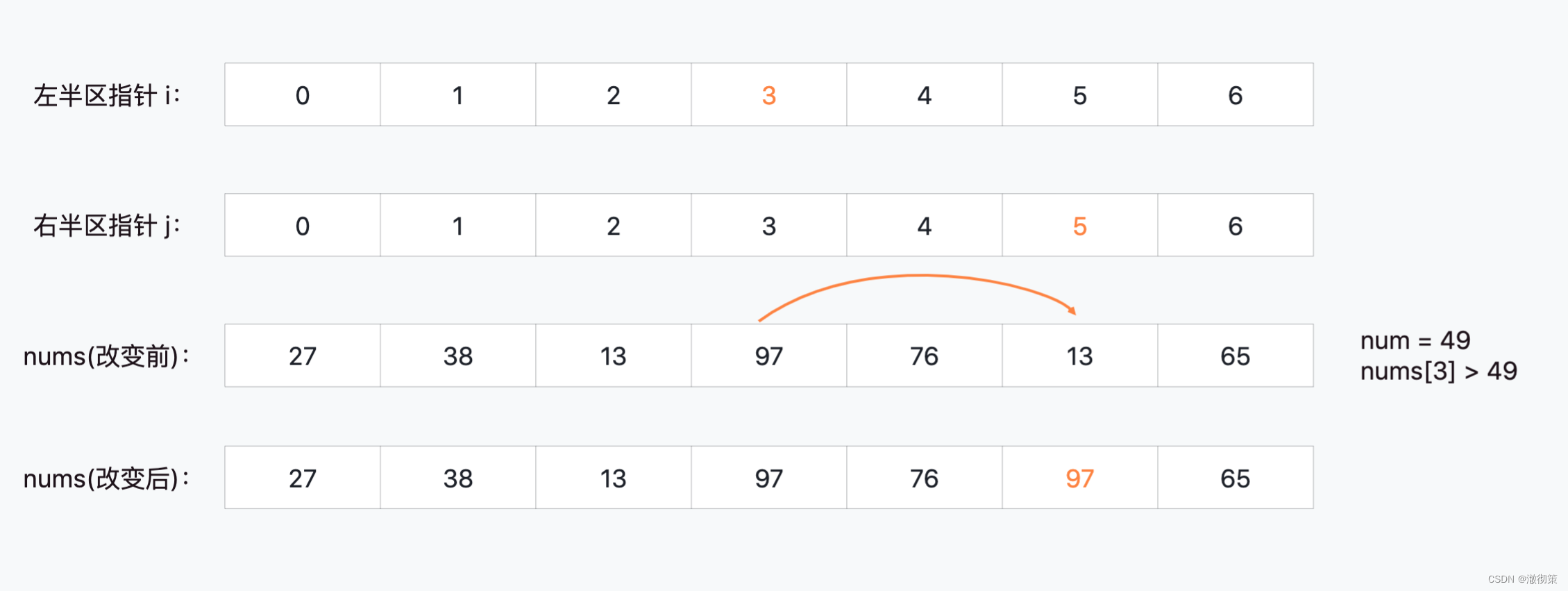
当i=3, j=4时，nums[4] > 49，符合预期，此时不做调整；

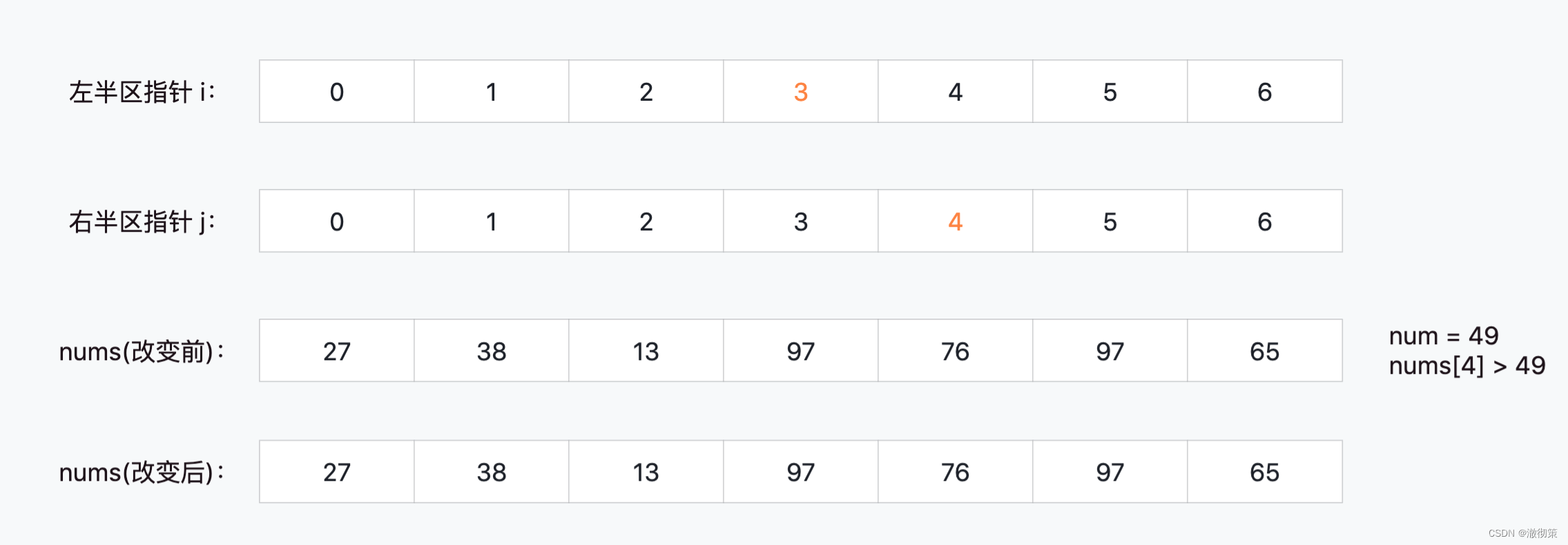
当i=3, j=3时，此时区间划分完毕，直接将49这个元素填到nums[3]中；

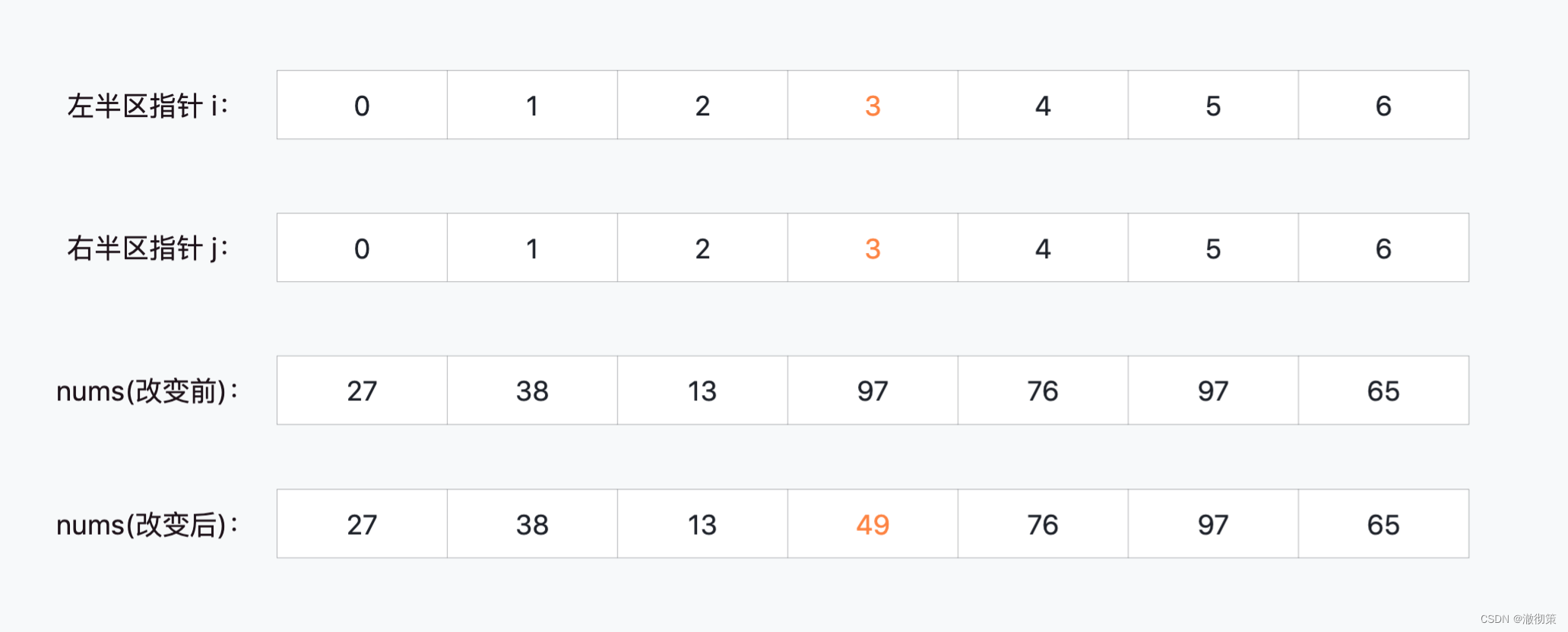
2**）第二轮区间划分（元素49的左半区间，选择第一个元素27）**

当i=1, j=1时，此时区间划分完毕，直接将27这个元素填到nums[1]中；

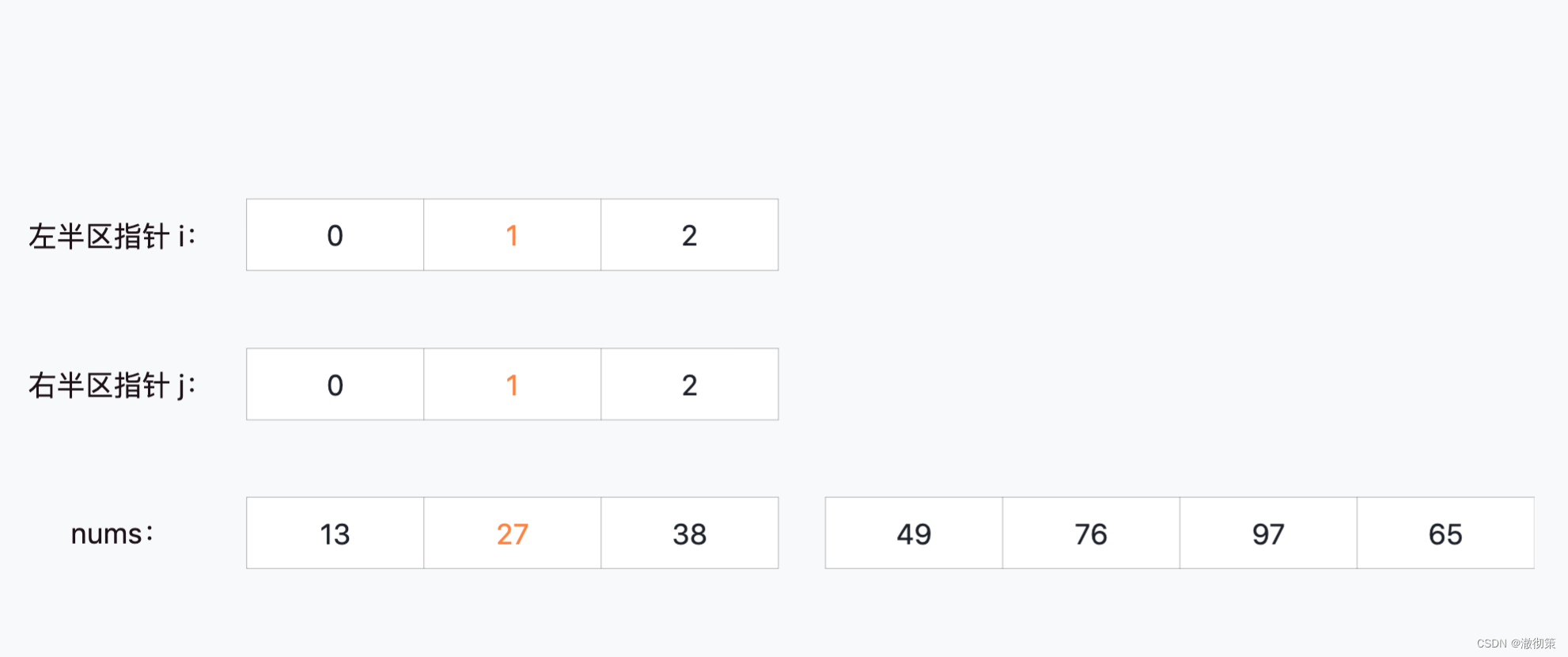
3**）第三轮区间划分（元素49的右半区间，选择第一个元素76）**

当i=5, j=5时，此时区间划分完毕，直接将76这个元素填到nums[5]中；

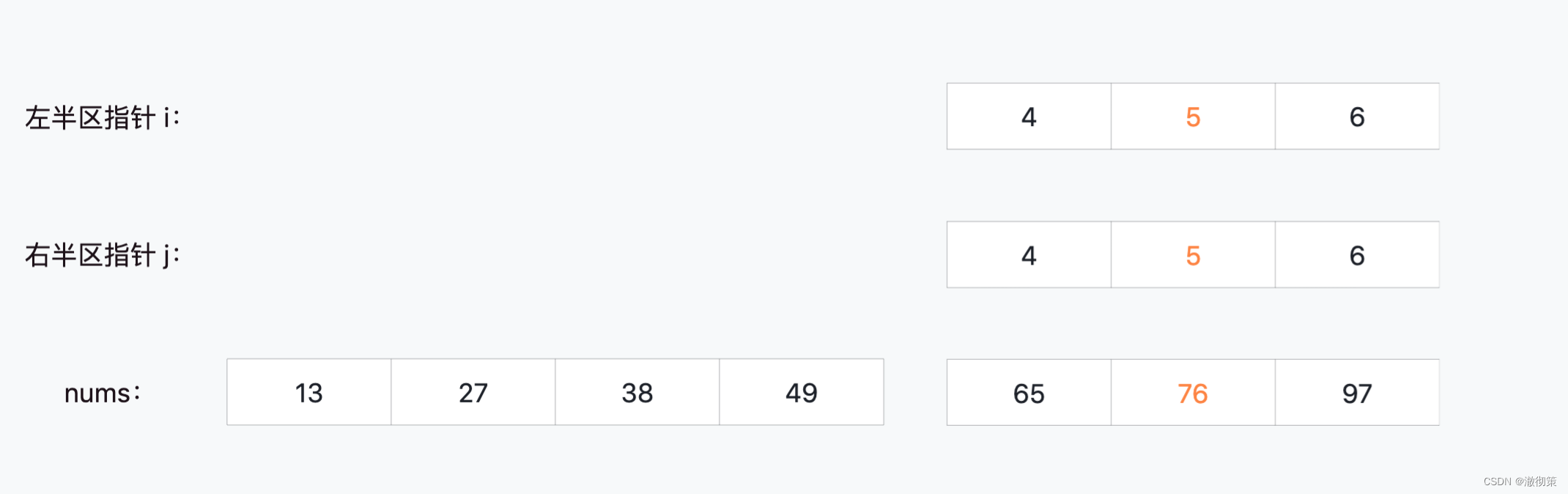
至此，整个快速排序的过程就分析完了，其求解的目标是将数组划分成左右两个区间，并利用分治的思想不停的划分下去，直到划分的区间内只有一个元素才会停止。

2.2 时间复杂度

对于nums = [49,38,65,97,76,13,27]这个输入，快速排序的的计算过程就像是一棵二叉树

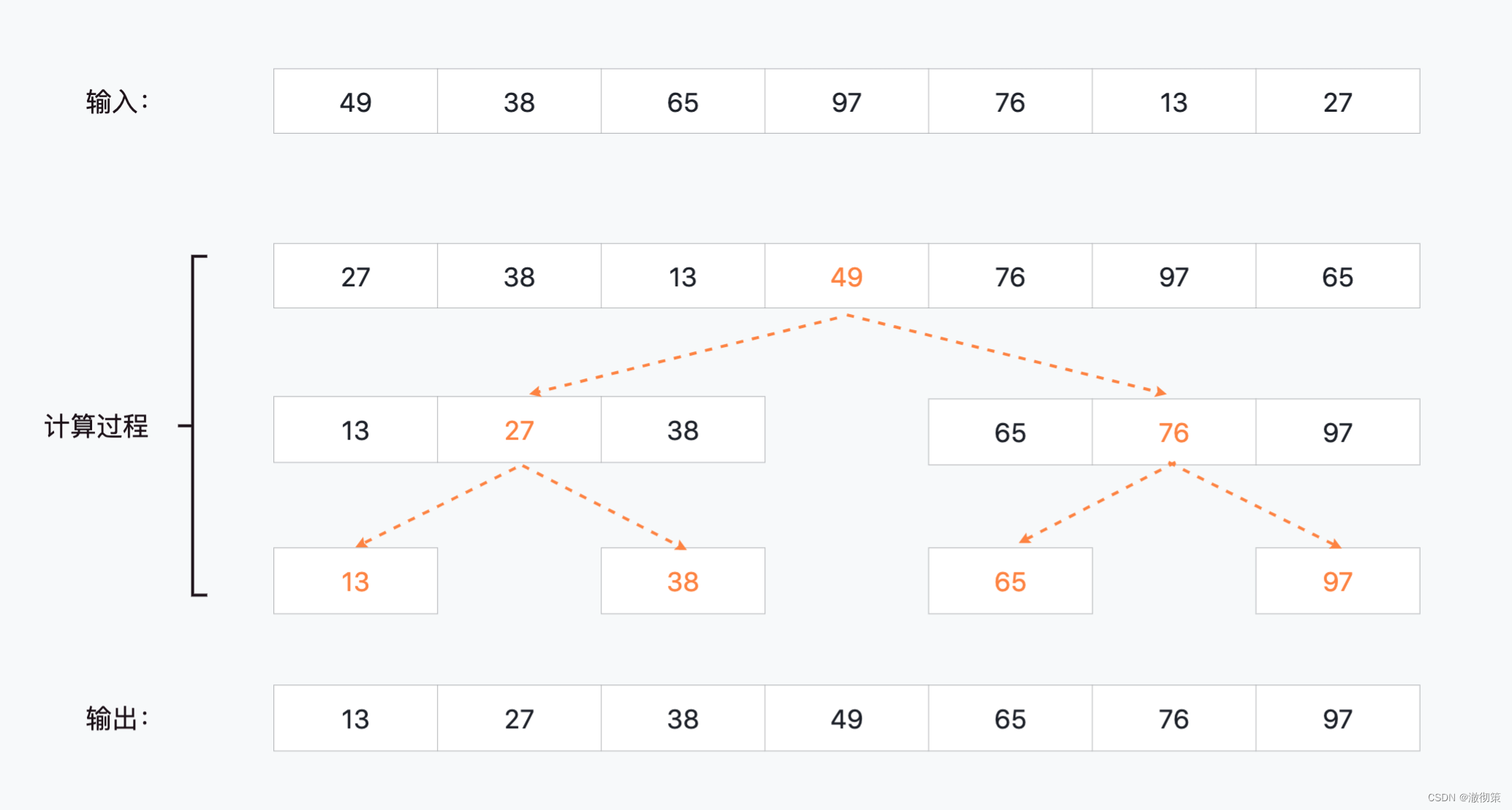
他的计算规模可以抽象地用一颗完全二叉树表示，该树总共有n个节点（n为输入数组的长度），其节点内的值表示当前层次中需要遍历的元素数量。

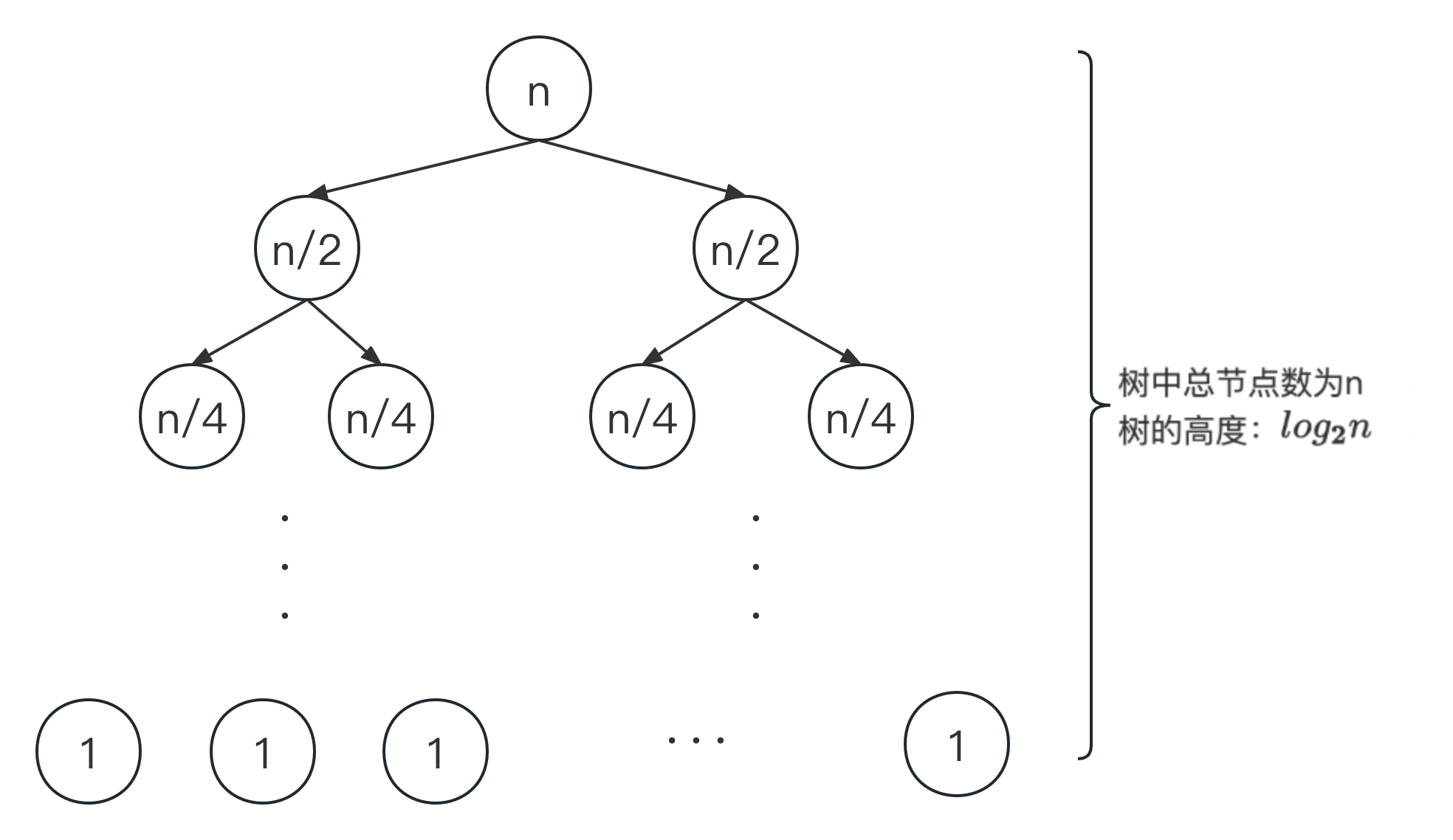
所以，快速排序的时间复杂度应该是树中节点总数 * 树的高度，即O(nlogn)。

2.2 代码实现

	public int[] sortArray2(int[] nums) {
		quickSort(nums, 0, nums.length - 1);
		return nums;
	}

	private void quickSort(int[] nums, int start, int end) {
		if (start >= end) {
			return;
		}
		
		int i = start;
		int j = end;
		int tmp = nums[i];
		// 将nums[i]为基准划分区间，并且保证其左边元素都小于nums[i]，右边元素都大于nums[i]
		while (i < j) {
			while (nums[j] >= tmp && i < j) {
				j--;
			}
			nums[i] = nums[j];
			while (nums[i] <= tmp && i < j) {
				i++;
			}
			nums[j] = nums[i];
		}
		nums[i] = tmp;

		// 分治递归左右两区间
		quickSort(nums, start, i - 1);
		quickSort(nums, i + 1, end);
	}

3. 归并排序

3.1 核心思想

将整个数组的排序问题，转换成了“子数组切分”和“两个有序子数组合并”的的问题

• 递归地将数组切分成多个子数组，直到长度为1时停止；
• 递归地对有序的子数组，进行两两合并，直到还原成原数组的长度；
  以nums = [49,38,65,97,76,13,27]为例，设置指针i,j分别表示当前切分的子数组的起始下标和结束下标，下面看看每一轮数组“切分-合并”的结果：
  

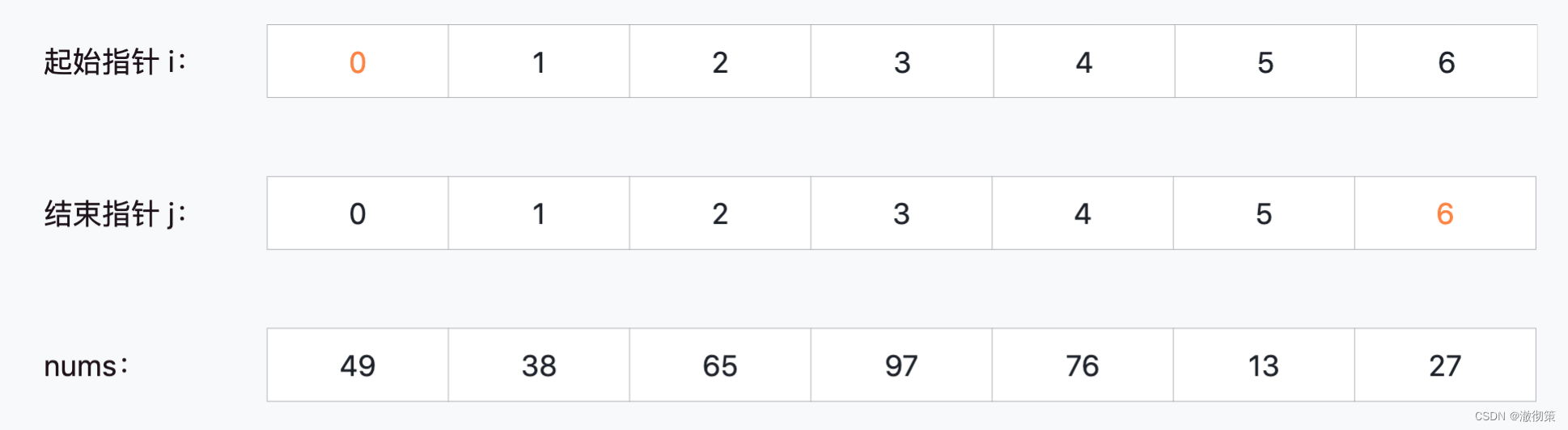
1）左半数组nums[0:3]

切分：i=0, j=3

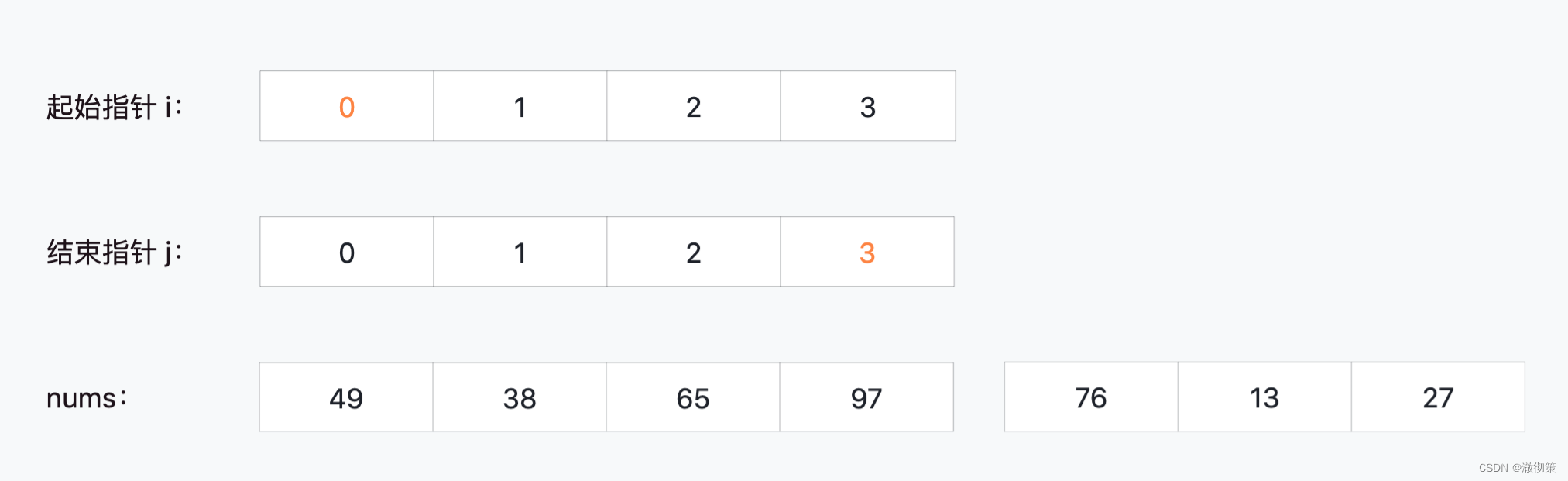
切分：i=0, j=1

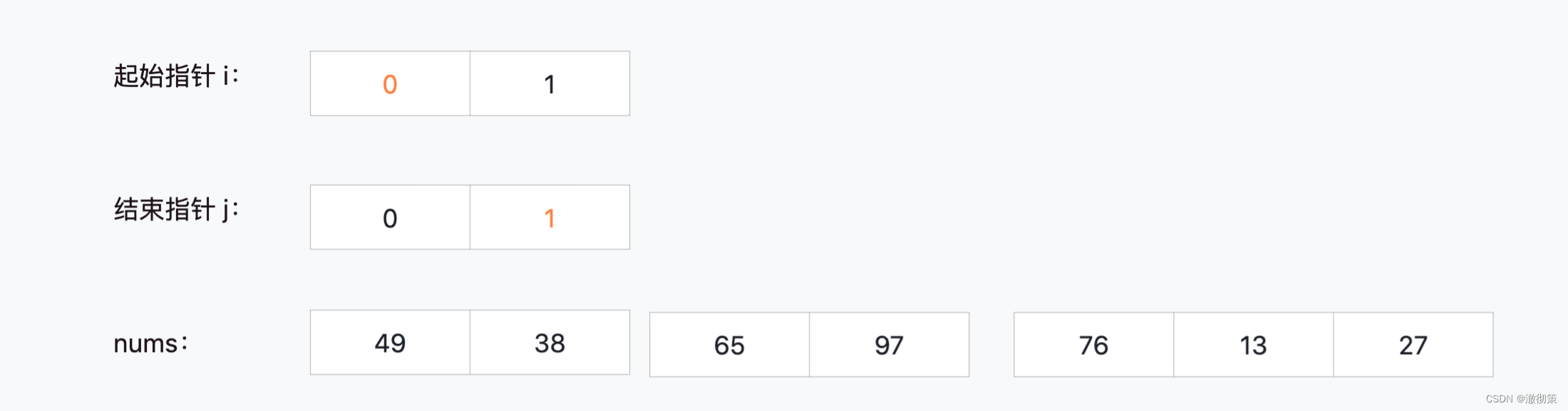
切分：i=0, j=0

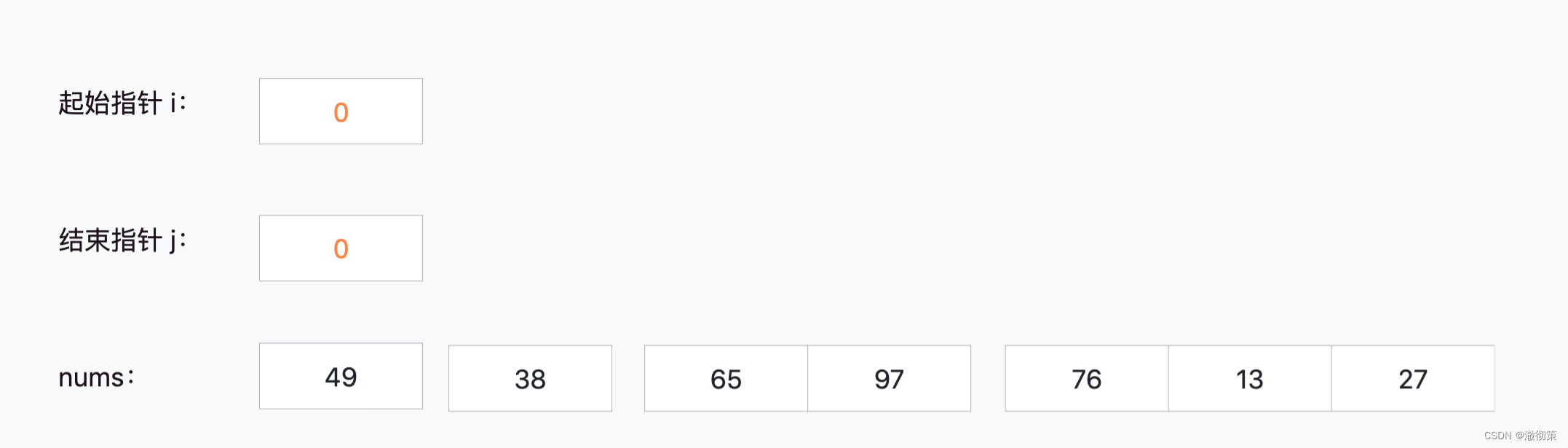
合并：i=0, j=1，nums[0] > nums[1]，需要交换位置

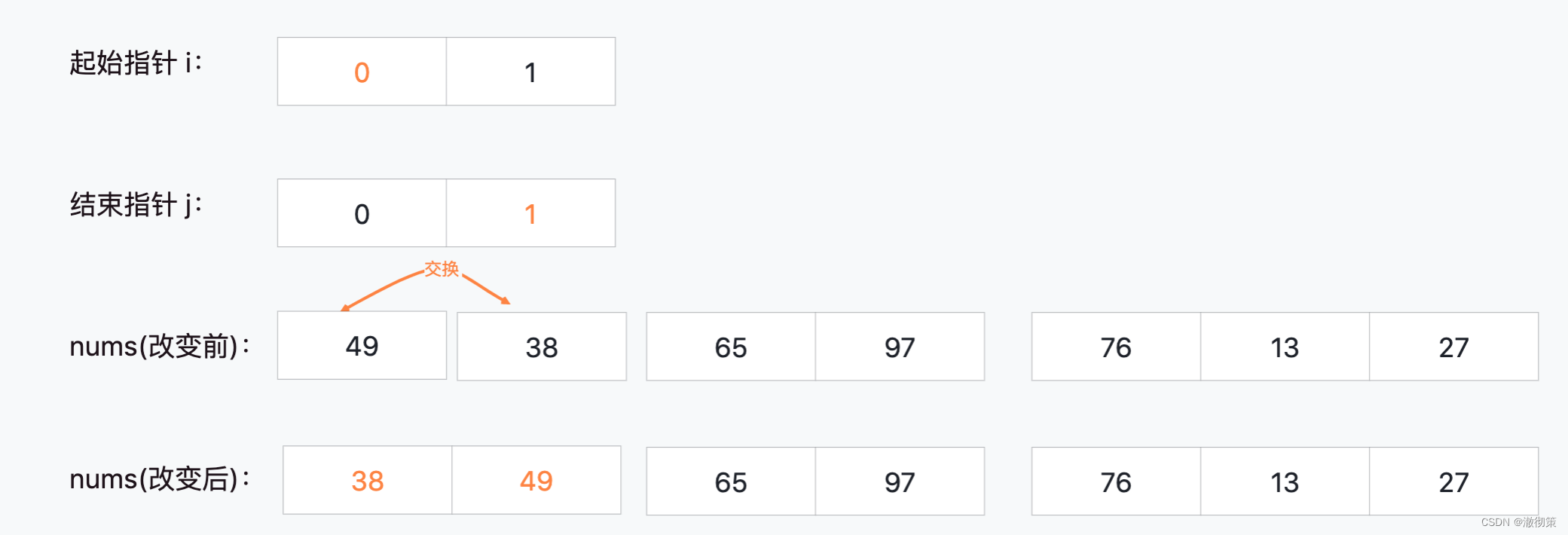
切分：i=2, j=2

合并：i=2, j=3，此时nums[2] < nums[3]，不需要改动

合并：i=0, j=3，至此左半区间就合并完成了

2）右半数组nums[4:6]

i=4,j=6

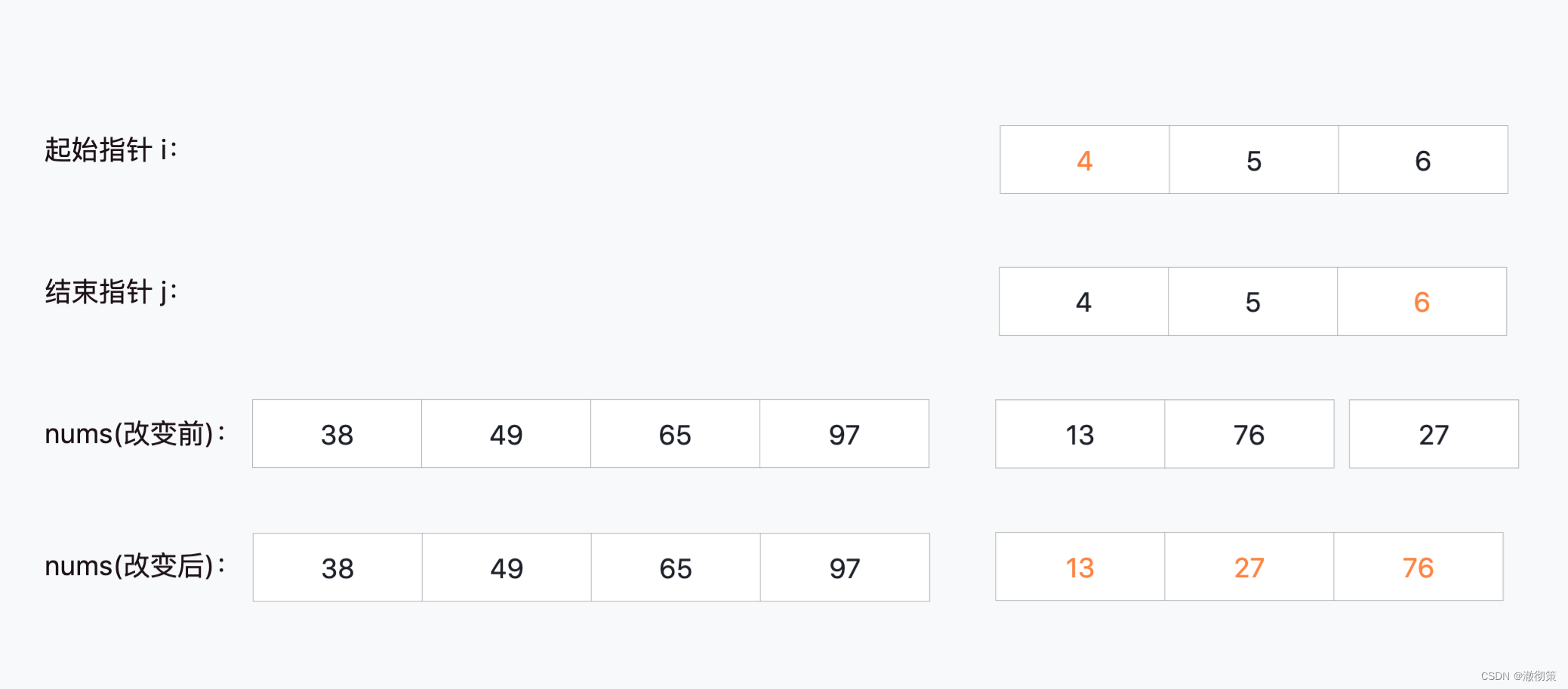
3**）整个nums数组**

i=0,j=6

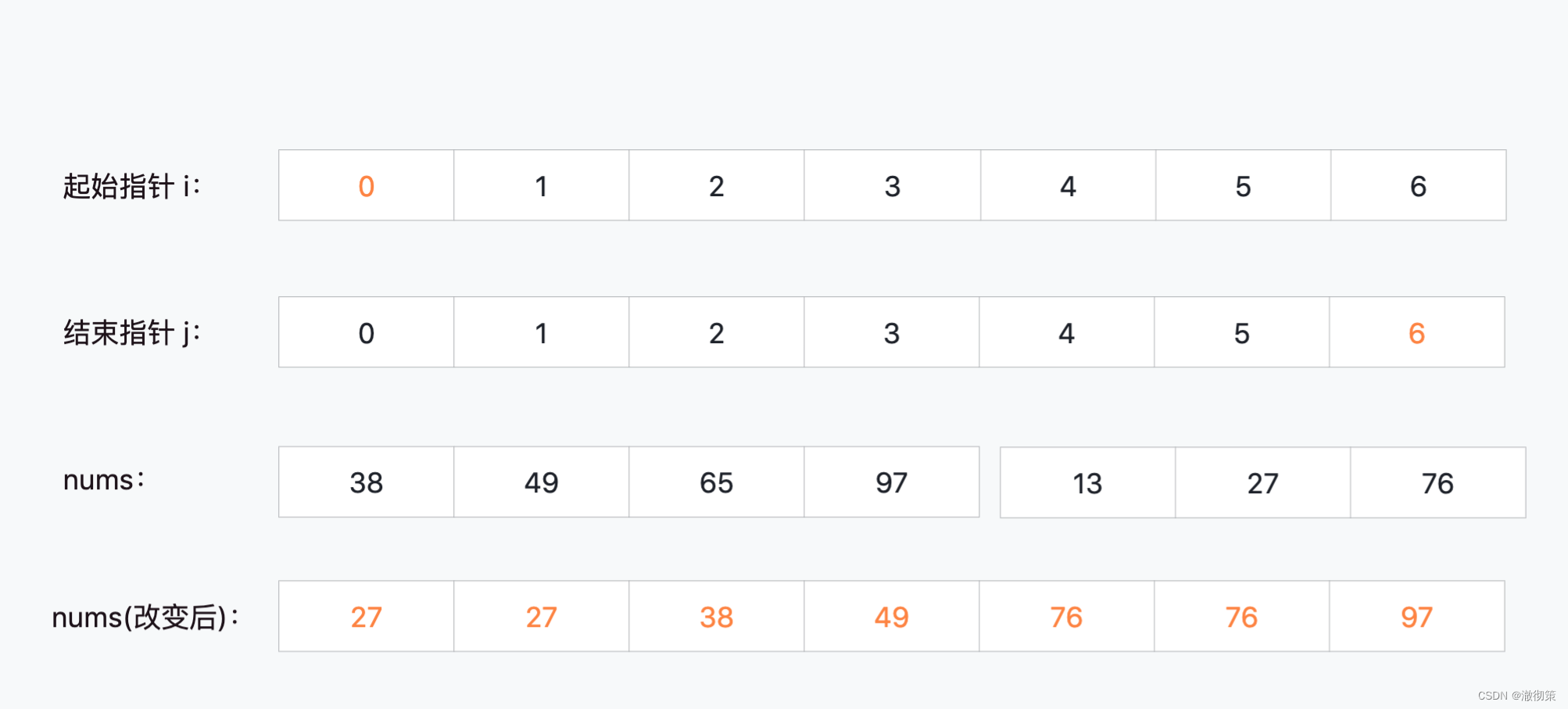
3.2 时间复杂度

对于nums = [49,38,65,97,76,13,27]这个输入的计算过程如下图所示：

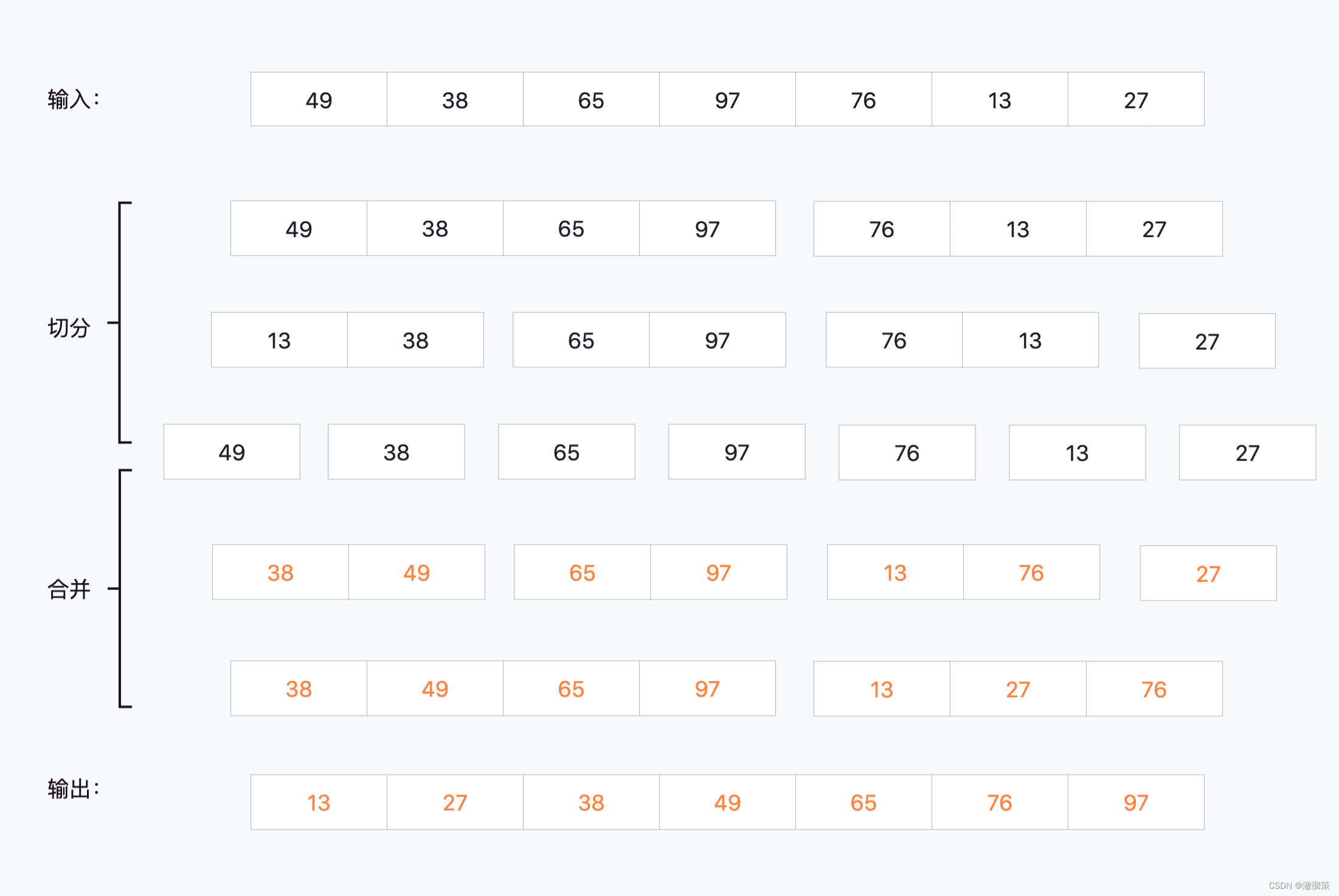
消耗时间的元素便利过程都集中在“合并”的过程中，可以将合并的过程看作是一颗**完全二叉树，**该树总共有n个节点（n为输入数组的长度），其节点内的值表示当前层次中需要遍历的元素数量。

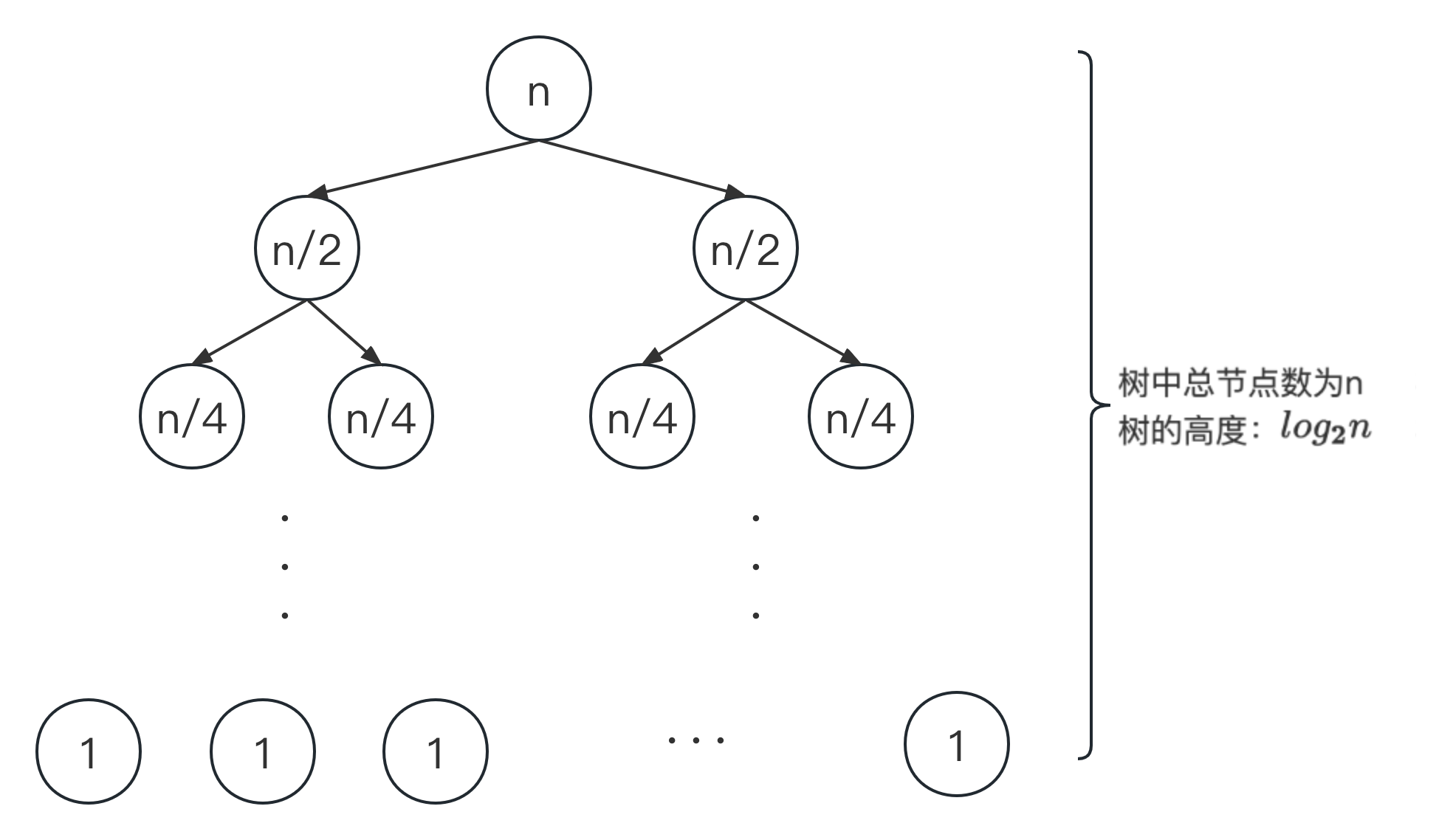
所以，归并排序的时间复杂度是树中节点总数 * 树的高度，即O(nlogn)。

3.3 代码实现

	public int[] sortArray3(int[] nums) {
		mergeSort(nums, 0, nums.length - 1);
		return nums;
	}

	private void mergeSort(int[] nums, int start, int end) {
		if (start >= end) {
			return;
		}
		int middle = (start + end) / 2;
		mergeSort(nums, start, middle);
		mergeSort(nums, middle + 1, end);
		merge(nums, start, middle, end);
	}

	// 调整区间[start, end有序]有序，其中[start, middle],[middle+1, end]区间已经有序
	private void merge(int[] nums, int start, int middle, int end) {
		int i = start; // 左半数组的起始下标
		int j = middle + 1; // 右半数组的起始下标

		int[] tmp = new int[end + 1]; // 暂存有序的nums数组
		int k = 0;
		while (i <= middle && j <= end) {
			if (nums[i] < nums[j]) {
				tmp[k++] = nums[i++];
			} else {
				tmp[k++] = nums[j++];
			}
		}
		// 如果还有一边的数组有多余元素，则直接复制到tmp中
		while (i <= middle) {
			tmp[k++] = nums[i++];
		}
		while (j <= end) {
			tmp[k++] = nums[j++];
		}
		// copy回原数组nums
		for (k = 0, i = start; i <= end; i++, k++) {
			nums[i] = tmp[k];
		}
	}