密码学简介
密码是经过加密过后的口令,是指用特定的变换对数据信息进行加密保护或者安全身份认证的物质和技术,密码学是对安全通信技术的研究,要能够有效的防范潜在攻击,也就是对信息加密解密的过程。
密码基本性质
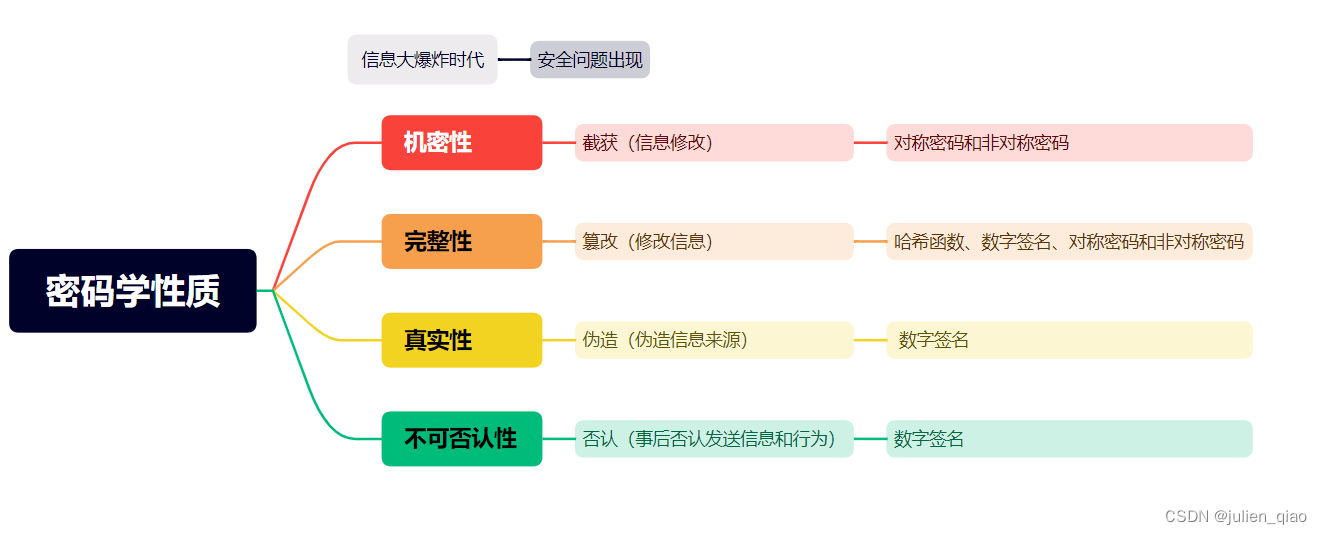
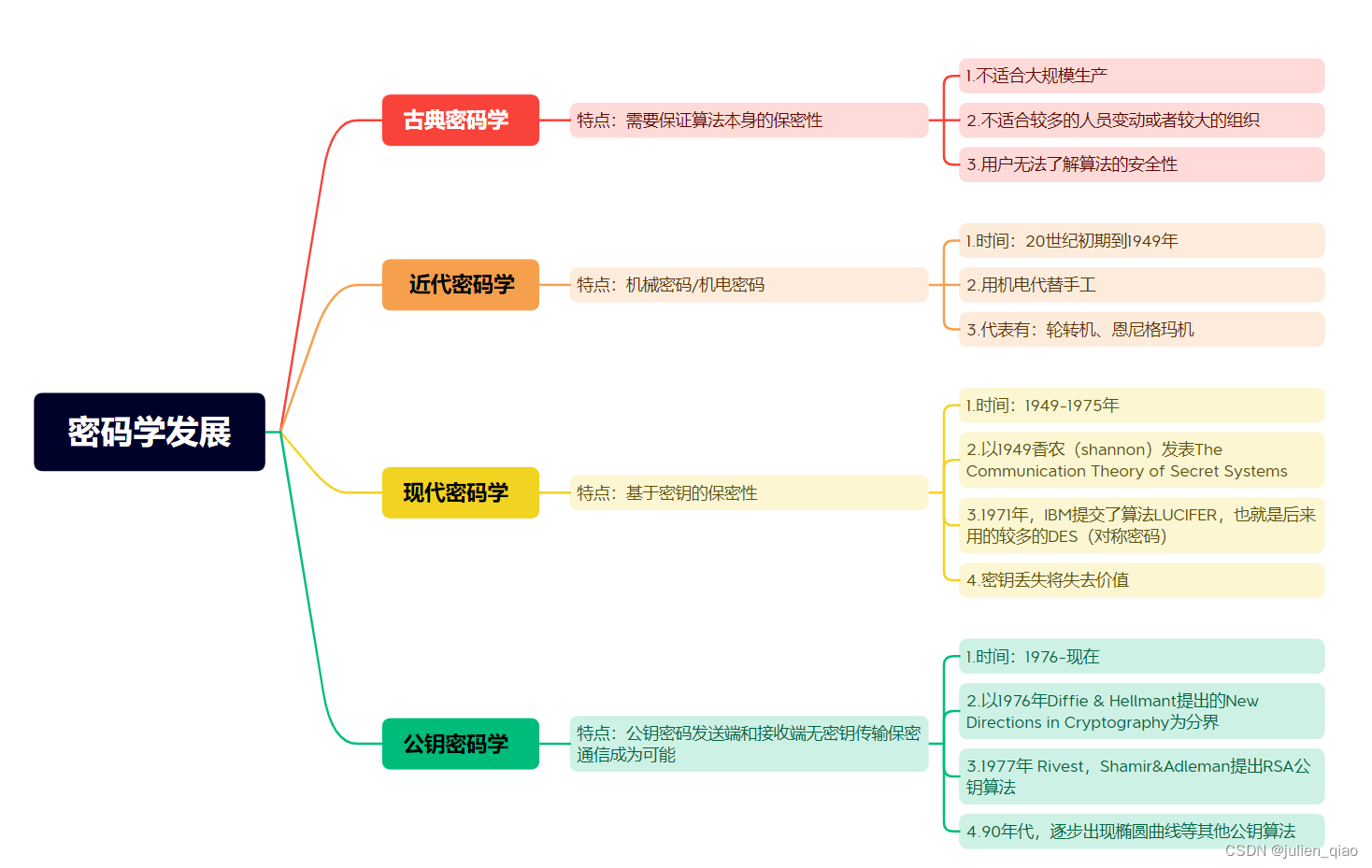
密码学的发展
古典密码到近代密码再到我们现在现在使用的公钥密码,密码学经历了四个阶段,每个阶段都以新技术的出现做为分界点。
加密与解密
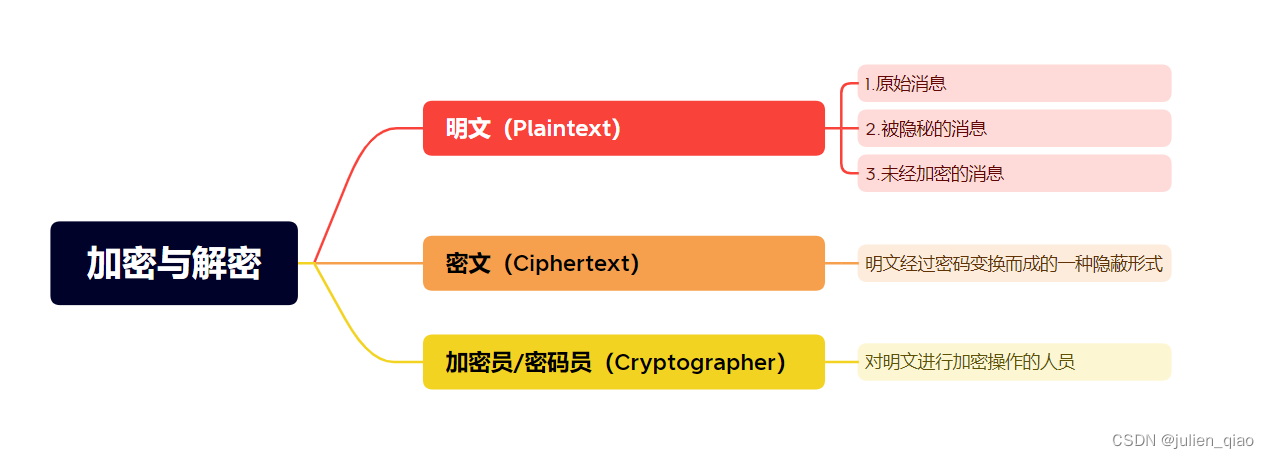
加密:由明文转换为密文的过程。
解密:由密文恢复出明文的过程。
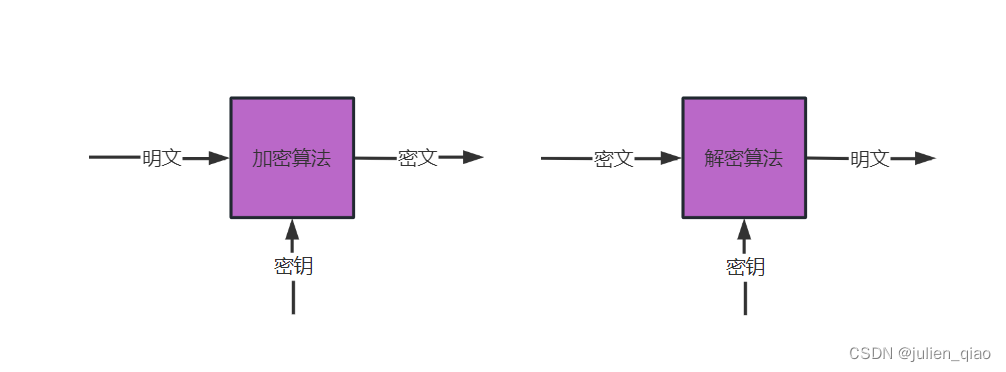
这里以古典密码为例:受算法保密性限制,如著名的凯撒密码就是古典密码一种,通过密码的位移进行加密,但是一旦公开算法,这种密码很容易被人破解。
凯撒密码:加密admin
from random import randint
import string
#凯撒加密
#加密
def kaisa(s, k): # 定义函数 接受一个字符串s 和 一个偏移量k
lower = string.ascii_lowercase # 小写字母
upper = string.ascii_uppercase # 大写字母
before = string.ascii_letters # 无偏移的字母顺序 小写+大写
after = lower[k:] + lower[:k] + upper[k:] + upper[:k] # 偏移后的字母顺序 还是小写+大写
# 分别把小写字母和大写字母偏移后再加到一起
table = ''.maketrans(before, after) # 创建映射表
return s.translate(table) # 对s进行偏移 即加密
s = input('请输入一个字符串:')
k = randint(0,26) #从0-25中挑选随机一个数字当做偏移量
print(kaisa(s, k))
解密脚本
LETTERS="ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz"
LETTERS1="ABCDEFGHIJKLMNOPQRSTUVWXYZ"
LETTERS2="abcdefghijklmnopqrstuvwxyz"
text=input("请输入密文:")
for key in range(len(LETTERS)):
str=""
for i in text:
if i in LETTERS:
if i.isupper(): #密文字母为大写
num = LETTERS1.find(i) #在字母里搜索到密文字符的位置
num = num - key
if num<0:
num = num + len(LETTERS1)
str = str + LETTERS1[num] #将解密后字符追加到字符串末尾
elif i.islower(): #密文字母为小写
num = LETTERS2.find(i) #在字母里搜索到密文字符的位置
num = num - key
if num<0:
num = num + len(LETTERS2)
str = str + LETTERS2[num] #将解密后字符追加到字符串末尾
else:
str = str + i #如果密文中内容不在字母里则不解密,直接追加
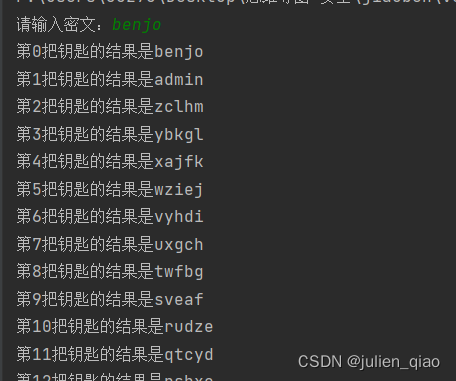
print('第%d把钥匙的结果是%s' %(key, str)) #显示每一个可能的值
这里通过穷举的方式得到明文admin
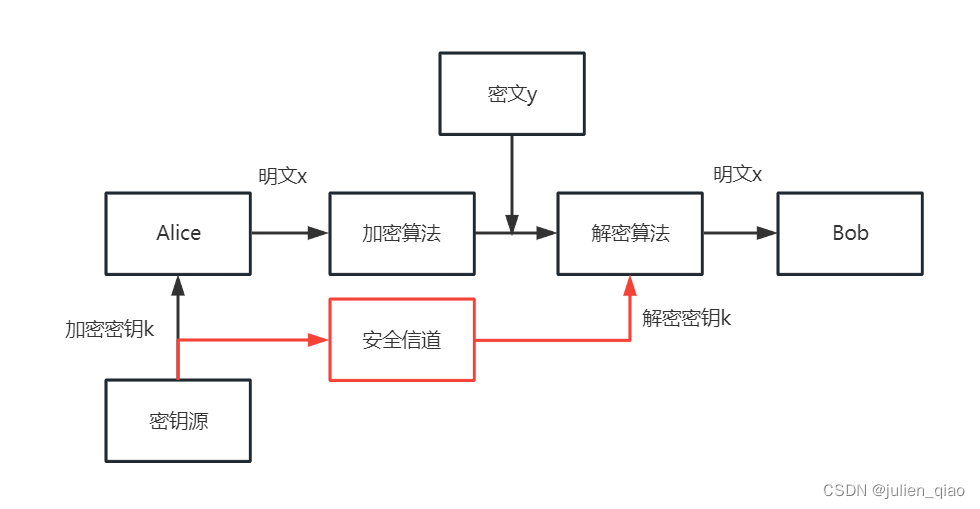
对称密码算法
对称密码算法(也称单钥或私钥密码算法):加密密钥和解密密钥相或实质上等同,即从一个易于推出另一个。
特点:
- DES、3DES、IDEA、AES
- 密钥相对较短,一般采用128,192或256比特大小
- 传输时采用安全信道传输密钥
优点: - 效率高,算法简单,系统开销小
- 适合加密大量数据
- 明文长度与密文长度相等
缺点: - 需要以安全方式进行密钥交换
- 密钥管理复杂
- 无法解决消息的篡改、否认等问题
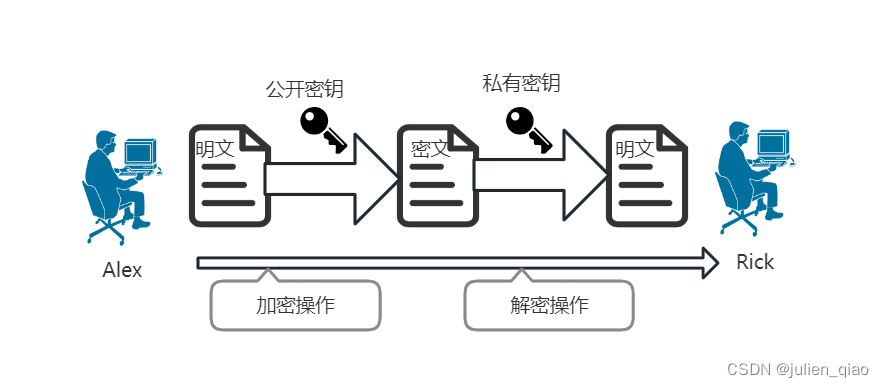
非对称密码算法
非对称密码算法:加密密钥和解密密钥不同,从一个很难推出另一个。其中,对外公开的密钥,称为公开密钥(public key),简称公钥;必须保密的密钥,称为私有密钥( private key) ,简称私钥。又叫公钥密码算法( Public-keycipher)。
特点
- RSA、ECC、ElGamal
- 公钥加密 私钥解密
- 私钥加密 公钥解密
- 密钥长度512-2048位
优点:
- 密钥分发数目与参与者数目相同
- 在有大量参与者的情况下易于密钥管理
- 安全
- 支持数字签名和不可否认性
- 无需事先与对方建立关系,交换密钥
缺点: - 速度相对较慢
- 可能比同等强度的对称密码算法慢10倍到100倍
- 加密后,密文变长
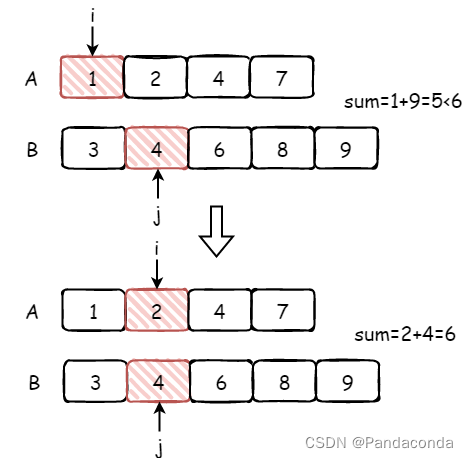
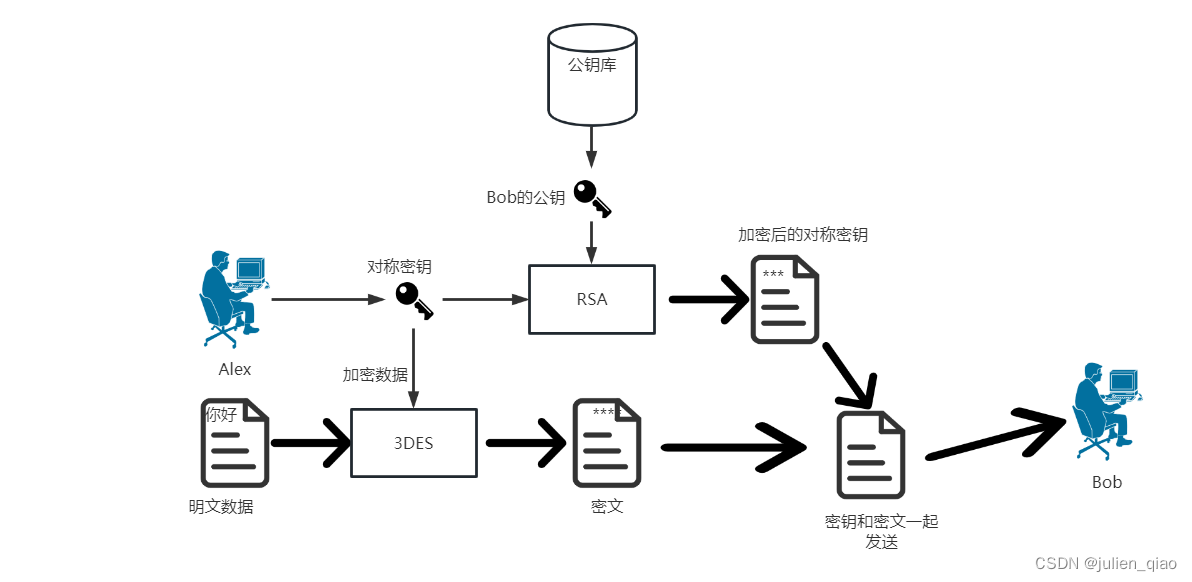
混合加密
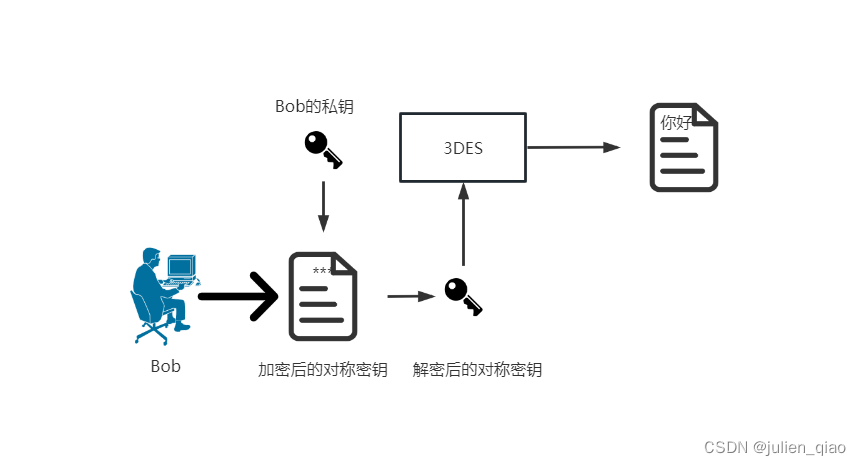
混合加密结合对称和非对称算法的特点进行组合而成,先是接收方将生成的公钥共享给发送方一份,发送方使用此公钥将生成的会话秘钥进行加密,同时发送方使用会话秘钥对明文内容进行加密,完成加密后,将两份加密过的内容一起发送给接收方,接收方接收到消息,先通过配对的私钥解密出会话秘钥,然后使用会话秘钥对密文进行解密,得到明文内容。
加密传输过程:
解密过程:
哈希函数
- 对称密码和非对称密码算法主要解决信息的机密性问题,而实际系统和网络还可能受到消息篡改等攻击。
- 篡改攻击主要包括:修改信息内容,改变程序使其不能正确·运行等。哈希函数可以用来保证信息的完整性。
- 哈希(Hash)函数(也称为杂凑函数或单向散列函数)接受一个消息作为输入,产生一个称为哈希值的输出。输出的哈希值也可称为散列值、消息摘要(MessageDigest, MD)
实验
哈希函数比较常用与下载的文件校验,通过文件算出哈希值进行比对文件是否被篡改。
创建一个index.html文件计算哈希值,对比修改后的哈希值,是否有变化。
修改前
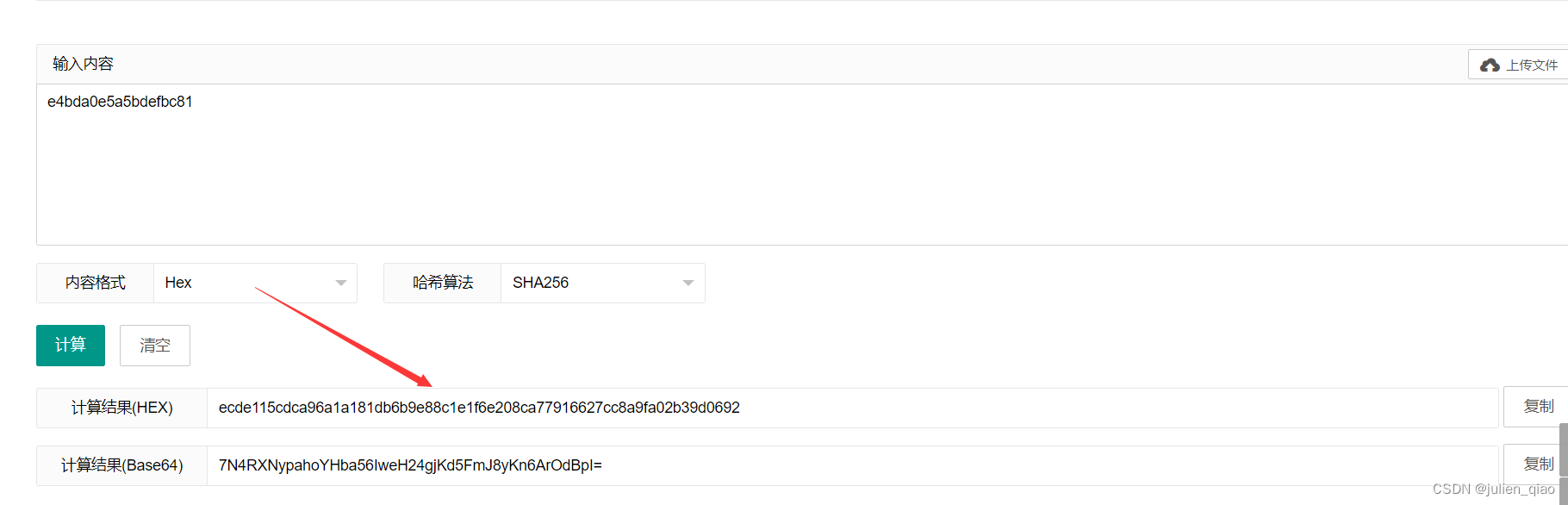
修改后发现有明显改变
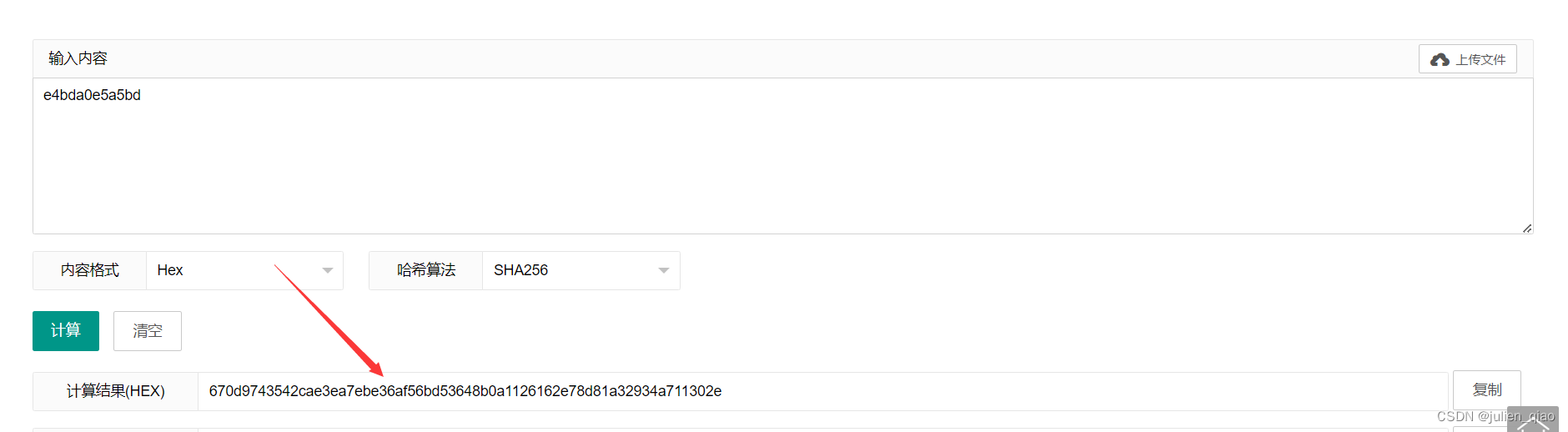
MD5
MD: Message Digest
消息摘要
- 输入:任意长度的消息
- 输出: 128位消息摘要
- 处理:以512位输入数据块为单位
SHA-1
SHA ( Secure Hash Algorithm ,安全哈希算法)由美国国家标准技术研究所开发,1993年作为联邦信息处理标准发布,2008 年又有更新。
- 输入:最大长度为264位的消息;
- 输出:160位消息摘要;
- 处理:输入以512位数据块为单位处理.
比较
- 散列值长度:MD5 128bits SHA1 160bits
- 安全性:SHA1算法被视为MD5的替代候选算法
- 速度:SHA1慢些 (openssl speed md5/sha1)
数字签名
除了保护信息的机密性和完整性,密码学技术也可以解决信息的可鉴别性(真实性或认证性)和不可否认性。
注意:数字签名是对文件的哈希值进行签名而不是对文件本身。
传统签名的基本特点:
- 能与被签的文件在物理上不可分割
- 签名者不能否认自己的签名
- 签名不能被伪造
- 容易被验证
数字签名是传统签名的数字化,基本要求: - 能与所签文件“绑定”
- 签名者不能否认自己的签名
- 签名不能被伪造
- 容易被验证
数字签名应用
- (1)可信性:签名让文件的接收者相信签名者是慎重地在文件上签名的。
- (2)不可重用性:签名不可重用,即使同一消息在不同时刻的签名也是有区别的。如果将签名部分提取出来,附加在别的消息后面,验证签名会失败。这是因为签名和所签名消息之间是一一对应的,消息不同签名内容也不同,因此签名无法重复使用。
- (3)数据完整性:在文件签名后,文件不能改变。
- (4)不可伪造性:签名能够证明是签名者而不是其他人在文件上签名,任何人都不能伪造签名。
- (5)不可否认性:在签名者否认自己的签名时,签名接收者可以请求可信第二方进行仲裁。







![[WUSTCTF2020]颜值成绩查询(布尔注入)](https://img-blog.csdnimg.cn/f3db04f98a9f4fdebdf0c3d8e7cd800f.png)