在光纤通信中,单模光纤在波长1.55μm窗口具有巨大的潜在带宽和极低的损耗,传输数字信号的容量已能达到10Tb/s,每信道光源功率仅需1mW左右,无中间放大的距离超过100km。而且,光纤作为光波导,红外光在其内部传输,不会向外辐射,对邻近光纤不会发生干扰,对人们的眼睛和身体不会造成伤害。与此相反,光无线系统的光源向自由空间大气发射,遭受的损耗较大,因而所需功率大大高于光纤通信用光源,但为防止对人眼引起伤害,必须对其功率进行适度控制,通常为几十毫瓦。而且光传输到接收端进行检测时,必定会有较大的耦合损耗,因此传输距离不能太长。由此可见,原来已很成熟的光纤通信技术不能完全照搬至光无线通信系统。
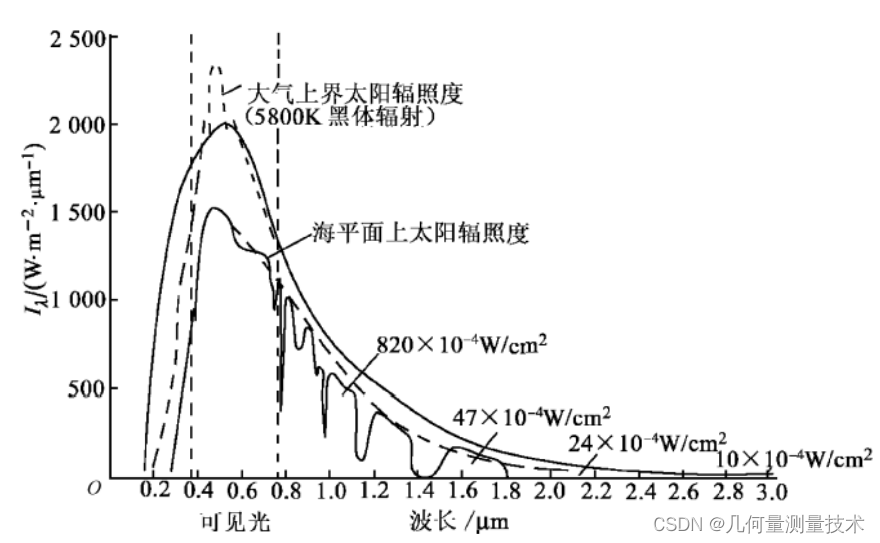
大气和地面对太阳光的散射形成的背景辐射,对激光大气通信的接收器来说是一个强的噪声源,如果阳光直射到探测器上,将会使误码率达到很高。 太阳辐照度的光谱可以用一个色温为5762K的黑体来表示,如下图所示。其辐照度光谱主要集中在400~750nm的可见光范围内,峰值在500nm左右。 对于常用的激光波段,800nm波段的辐射强度约为峰值的1/2,1060nm波段的辐射强度约为峰值的1/3,1500~1600nm波段的辐射强度约为峰值的1/10,在紫外波段,300nm波段附近辐射降到峰值的1/10以下,波长进一步缩短时,太阳的辐照度迅速下降。 显然,为减小背景辐射的影响,不宜采用可见波段的激光,紫外和红外光是可选择对象。
大气透过率是选择激光波长时需考虑的一个重要因素。 地球表面的大气层中存在着多种气体以及各种微粒,如尘埃、烟、雾、小水滴等。还可能要发生各种复杂的气象现象,如雨、雾、 雪、风等。这些因素,对光波有衰减作用,会使激光能量大大减小,或者使激光偏离原来的传输方向,破坏了激光原有的特性。单色光的大气透过率可表示为:
τ
(
λ
,
z
)
=
P
(
z
)
P
(
0
)
=
e
−
σ
(
λ
)
z
\begin{equation}τ(λ,z)=\frac{P(z)}{P(0)}=e^{-σ(λ)z}\end{equation}
τ(λ,z)=P(0)P(z)=e−σ(λ)z
公式中
P
(
0
)
P(0)
P(0)为光源处的激光功率,
P
(
z
)
P(z)
P(z)为传输距离
z
z
z处的激光功率,
σ
(
λ
)
σ(λ)
σ(λ)为大气总的衰减系数,它由四个部分组成:
σ
(
λ
)
=
σ
m
+
σ
a
+
K
m
+
K
a
\begin{equation}σ(λ)=σ_m+σ_a+K_m+K_a\end{equation}
σ(λ)=σm+σa+Km+Ka
上述公式
σ
m
σ_m
σm为气体分子或瑞利散射系数,
σ
a
σ_a
σa为气体中的悬浮微粒或米式散射系数,
K
m
K_m
Km为分子吸收系数,
K
a
K_a
Ka为悬浮微粒的吸收系数。
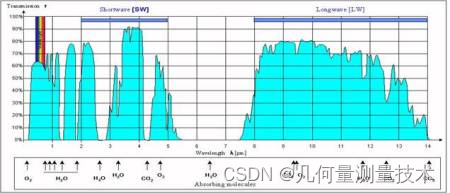
大气吸收是将辐射能量转换成大气组成分子的运动。 大气中对太阳辐射的主要吸收体是水蒸汽、二氧化碳和臭氧。这些气体分子或蒸汽分子的吸收是具有选择性的。 能见度大于31km 的极晴朗天气下,如图所示,波长从 0.3~5μm,不同天顶角时穿过整个大气层的透射率。 在小于300nm 的紫外波段,大气的透过率急剧下降。 显然, 紫外激光也不利于激光在大气中传输。 对于常用的红外激光波段,810~860nm、980~1 060nm 和1550~1600nm 波段都是良好的大气窗口。
大气的散射是由大气中不同大小的颗粒的反射或折射所造成的,这些颗 粒包括组成大气的气体分子、灰尘和大的水滴。 纯散射没有能量的损失,它只是改变了能量的分配方向。 大气对光的散射主要有瑞利散射、米氏散射和非选择性散射( 又称几何散射) 。当散射颗粒的大小比辐射波长小得多时,会发生瑞利散射,瑞利散射系数与波长的四次方成反比; 当散射颗粒的大小可以与辐射波长相比拟时,会发生米氏散射。 瑞利散射和米氏散射都具有波长选择性,波长越长散射越小。 米氏理论适用于如小雨、雾滴、霾等球形粒子。 一般说来,对于半径r≤0.3μm的粒子,波长在1μm附近,瑞利定律的误差≤1%, 当粒子半径r>0.3μm时,须采用米氏定律。当粒子半径比辐射波长至少大40μm 时才出现非选择性散射。低层大气的主导衰减仅是米氏散射。这时衰减系数
σ
(
λ
)
σ(λ)
σ(λ)可以用与能见度有关的经验公式表示,其形式为:
σ
(
λ
)
=
3.91
V
(
λ
550
)
−
q
\begin{equation}σ(λ)=\frac{3.91}{V}(\frac{λ}{550})^{-q}\end{equation}
σ(λ)=V3.91(550λ)−q
公式(3)中,
V
V
V表示能见度(km),
λ
λ
λ为传输波长(nm)。
q
q
q与能见度有关,较传统的观点认为他们之间的关系如下:
q
=
{
1.6
(
V
>
50
km
)
1.3
(
6
<
V
<
50
km
)
0.585
V
1
/
3
(
V
<
6
km
)
\begin{equation}q=\left\{ \begin{aligned} 1.6 & &(V>50\text{km}) \\ 1.3 & & (6<V<50\text{km})\\ 0.585V^{1/3} & & (V<6\text{km}) \end{aligned} \right.\end{equation}
q=⎩
⎨
⎧1.61.30.585V1/3(V>50km)(6<V<50km)(V<6km)
由(4)式,人们推断1550nm的光在任何天气情况下的衰减系数都比785nm的光小,然而文献报导实验情况并非如此。在阴霾天及更好的天气情况下1550nm的衰减系数确实比785nm 的光小,但是在雾天,两者的衰减系数是一样的。当能见度小于500m时,衰减系数与波长无关,即产生非选择性散射。 因此他们将
q
q
q值修正为:
q
=
{
1.6
(
V
>
50
km
)
1.3
(
6
<
V
<
50
km
)
0.16
V
+
0.34
(
1
<
V
<
6
km
)
V
−
0.5
(
0.5
<
V
<
1
km
)
0
(
V
<
0.5
km
)
\begin{equation}q=\left\{ \begin{aligned} 1.6 & &(V>50\text{km}) \\ 1.3 & & (6<V<50\text{km})\\ 0.16V+0.34 & & (1<V<6\text{km})\\ V-0.5 & & (0.5<V<1\text{km})\\ 0 & & (V<0.5\text{km}) \end{aligned} \right.\end{equation}
q=⎩
⎨
⎧1.61.30.16V+0.34V−0.50(V>50km)(6<V<50km)(1<V<6km)(0.5<V<1km)(V<0.5km)
把公式(3)带入到公式1,可以得到:
τ
(
λ
,
z
)
=
P
(
z
)
P
(
0
)
=
e
−
3.91
V
(
λ
550
)
−
q
z
\begin{equation}τ(λ,z)=\frac{P(z)}{P(0)}=e^{-\frac{3.91}{V}(\frac{λ}{550})^{-q}z}\end{equation}
τ(λ,z)=P(0)P(z)=e−V3.91(550λ)−qz
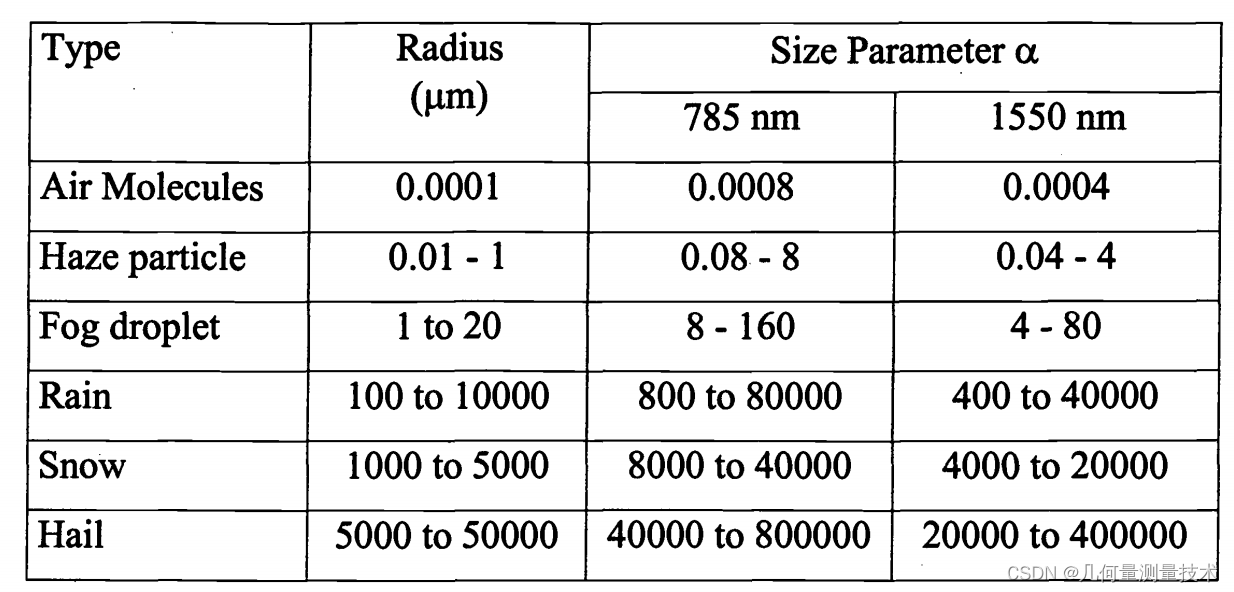
公式(6)非常清晰地描述了透过率是由哪些因素决定的。下图展示了雨水、雾等典型颗粒的部分参数:
衰减源自空气中气溶胶和分子的吸收和散射,吸收部分其实很少,主要是散射。散射类型是由粒径尺寸和激光波长决定的,这里可以定义一个新变量
α
\alpha
α,表示为:
α
=
2
π
r
λ
\begin{equation}\alpha=\frac{2\pi r}{λ}\end{equation}
α=λ2πr
对于785nm和1550nm的激光波长,
α
\alpha
α和粒径尺寸参数的关系可以表示为如下图所示:
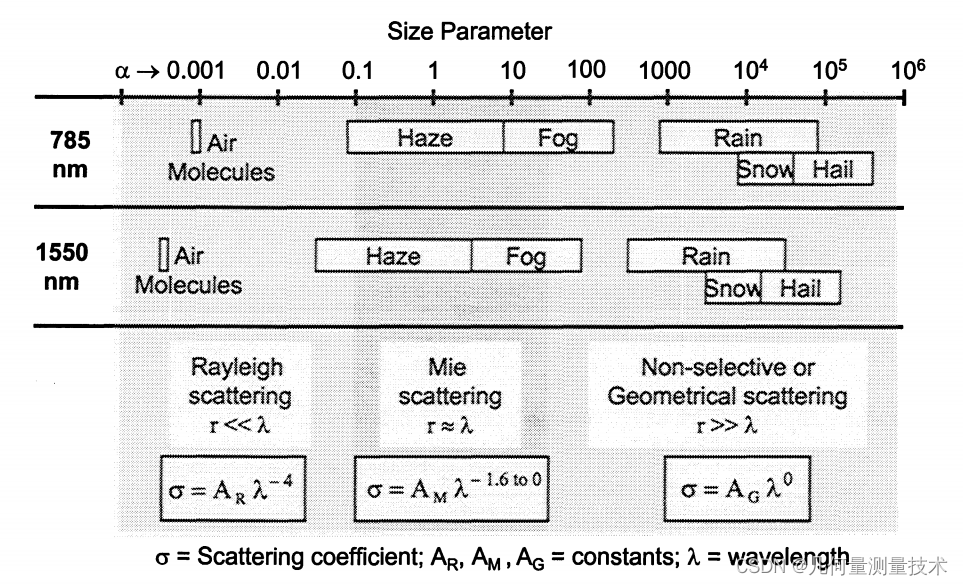
从图中可见,当粒径
r
r
r和波长
λ
λ
λ的大小关系呈现不同状态时,散射类型是不同的(Rayleigh、Mie和Non-selective/Geometrical)。所以波长越大,散射系数
σ
\sigma
σ越小,透射率就越高。关于大气散射的波长依赖性(wavelength dependence),定义了一个散射效率系数
Q
Q
Q,表示为:
Q
=
C
2
π
r
\begin{equation}Q=\frac{C}{2\pi r}\end{equation}
Q=2πrC
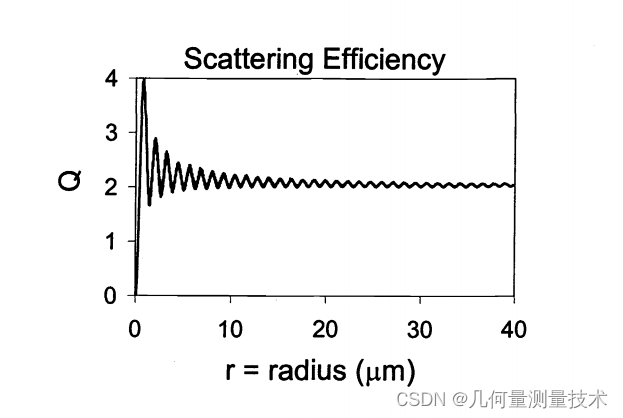
r
r
r代表粒子半径。散射效率是粒径的函数,下图表示的就是785nm波长激光在反射率
σ
\sigma
σ为1.33是水粒子的散射效率。
如果散射粒子半径分布式确定的,整个散射系数
σ
\sigma
σ可以通过把每个粒径尺寸分布进行求和得到:
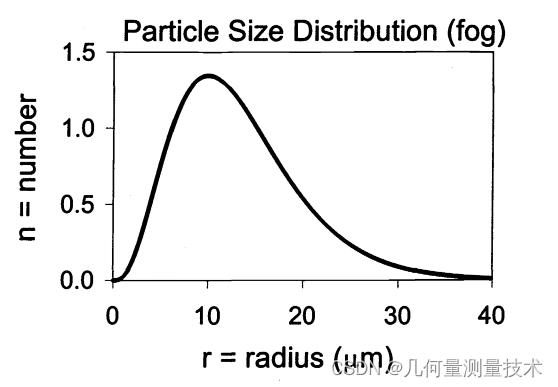
σ s c a t = ∑ i n i Q i π r i 2 \begin{equation}\sigma_{scat}=\sum\limits_{i}n_iQ_i\pi r_i^2\end{equation} σscat=i∑niQiπri2其中, n i n_i ni表示第 i i i个粒子的分布。雾(fog)的粒径分布如下图所示:
 还可以针对已知粒径分布基于完整的Mie计算理论确定波长依赖性,一个流行的分析大气粒径分布模型是由Deirmendjian修改的gamma分布模型。
还可以针对已知粒径分布基于完整的Mie计算理论确定波长依赖性,一个流行的分析大气粒径分布模型是由Deirmendjian修改的gamma分布模型。