常见的api：BigDecima

news2024/7/6 19:52:04

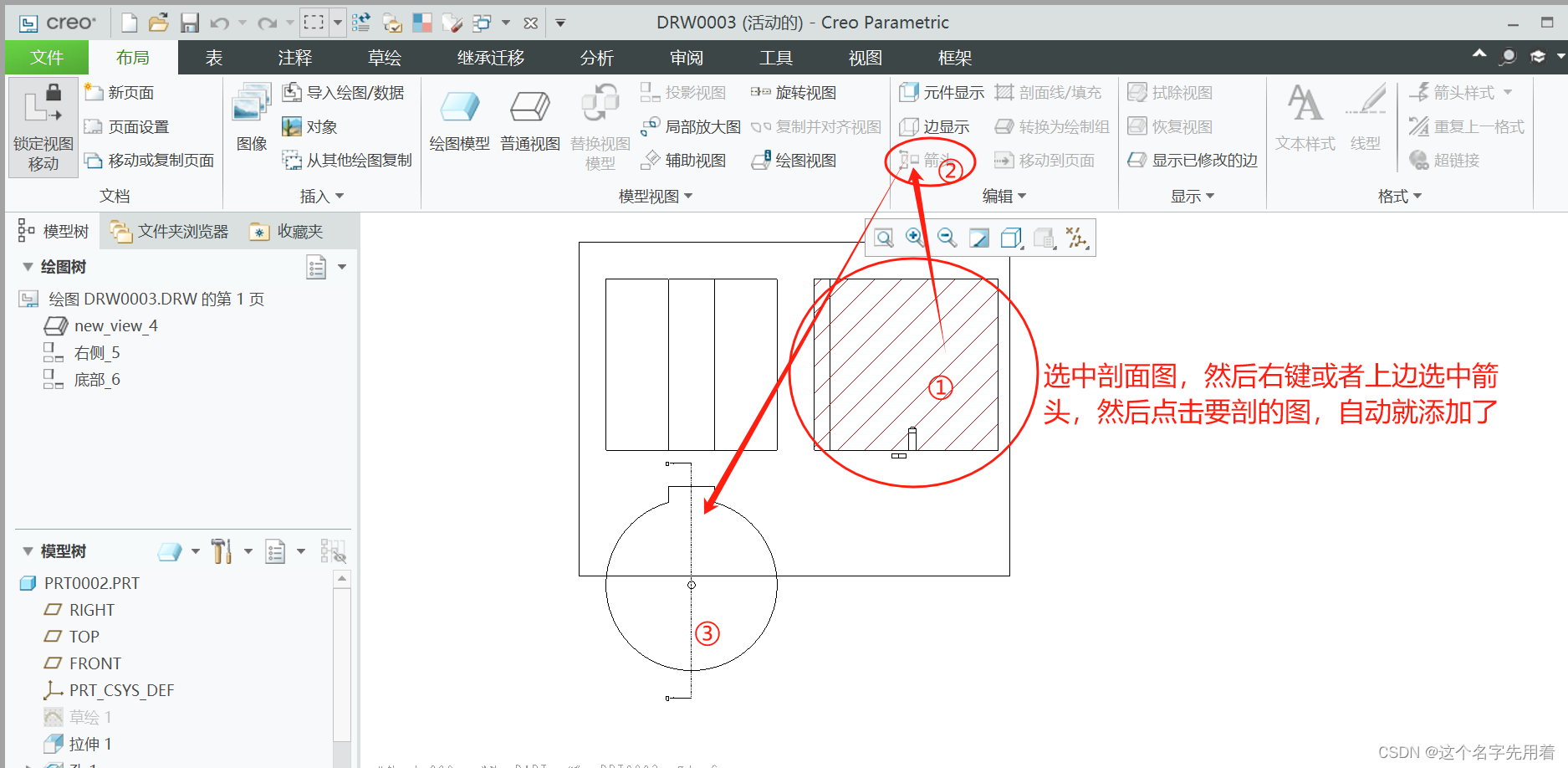
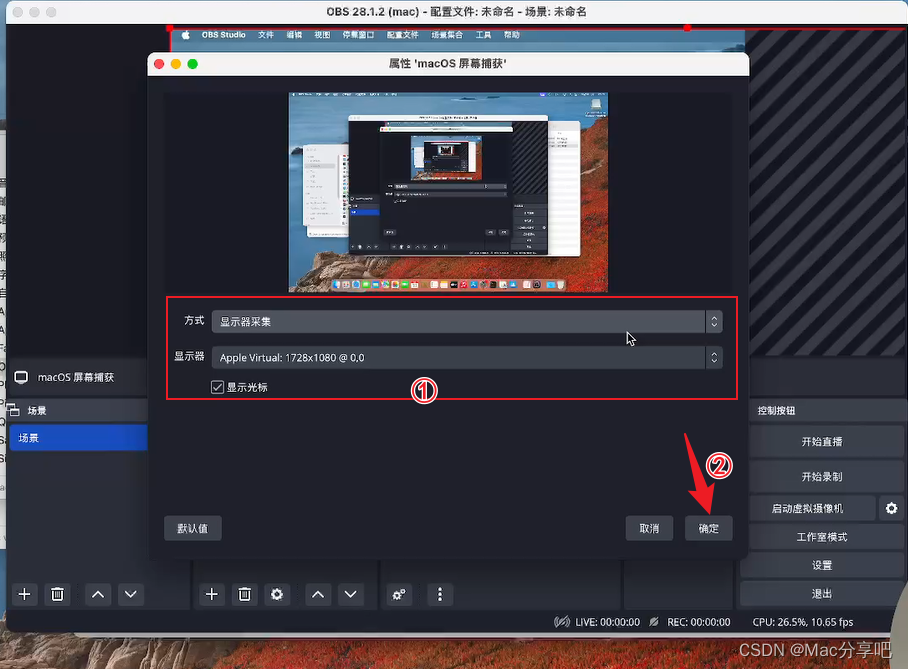
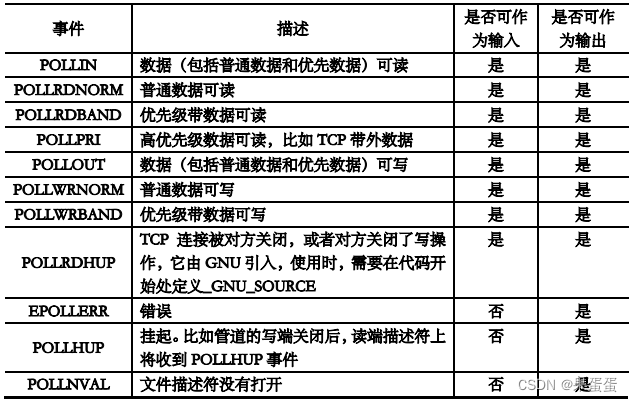
一.计算中的小数

float和double占有的位置是有限的

二.BigDecima的作用

1.用于小数的精确计算

2.用来表示很大的小数

三.使用(传入小数)

  BigDecimal b1 = new BigDecimal(0.01);
        BigDecimal b2 = new BigDecimal(0.09);
        System.out.println(b1);
        System.out.println(b2);

不精确：

0.01000000000000000020816681711721685132943093776702880859375
0.0899999999999999966693309261245303787291049957275390625

四.传入字符串

     BigDecimal b1 = new BigDecimal("0.01");
        BigDecimal b2 = new BigDecimal("0.09");
        BigDecimal b3 = b1.add(b2);
        System.out.println(b3);

五.通过静态方法获取对象

   BigDecimal bd6 = BigDecimal.valueOf(10);
   System.out.println(bd6);

六.细节

1.如果表示的数字不大,没有超出double的取值范围,建议使用静态方法。

2.如果表示的数字比较大超过的double的取值范围,建议使用构造方法。

3.如果我们传递的是0-10之间的整数，包含0，包含10，那么方法会返回创造好的对象,不会重写new。

  BigDecimal bd6 = BigDecimal.valueOf(10);
        BigDecimal bd7 = BigDecimal.valueOf(10);
        System.out.println(bd6 == bd7); //true

如果是传递的是double的浮点数直接是new出来的

  BigDecimal bd6 = BigDecimal.valueOf(10.0);
        BigDecimal bd7 = BigDecimal.valueOf(10.0);
        System.out.println(bd6 == bd7); //false

七.常见的成员方法

1.加法

   BigDecimal Bd1 = BigDecimal.valueOf(10.0);
        BigDecimal Bd2 = BigDecimal.valueOf(2.0);
        BigDecimal Bd3 = Bd1.add(Bd2);
        System.out.println(Bd3);  //12.0

2.减法

  BigDecimal Bd1 = BigDecimal.valueOf(10.0);
        BigDecimal Bd2 = BigDecimal.valueOf(2.0);
        BigDecimal Bd3 = Bd1.subtract(Bd2);
        System.out.println(Bd3); //8.0

3.乘法

    BigDecimal Bd1 = BigDecimal.valueOf(10.0);
        BigDecimal Bd2 = BigDecimal.valueOf(2.0);
        BigDecimal Bd3 = Bd1.multiply(Bd2);
        System.out.println(Bd3); //20.00

4.除法

  BigDecimal Bd1 = BigDecimal.valueOf(10.0);
        BigDecimal Bd2 = BigDecimal.valueOf(2.0);
        BigDecimal Bd3 = Bd1.divide(Bd2);
        System.out.println(Bd3); //5

5.除不尽（要除的数,保留几位小数,四舍五入的模式）

   BigDecimal Bd1 = BigDecimal.valueOf(10.0);
        BigDecimal Bd2 = BigDecimal.valueOf(3.0);
        BigDecimal Bd3 = Bd1.divide(Bd2, 2, RoundingMode.UP);
        System.out.println(Bd3);