概述

上两篇文章，我们依次讲解了树、二叉树、二叉查找树。二叉查找树是最常用的一种二叉树，它支持快速插入、删除、查找操作，各个操作的时间复杂度跟树的高度成正比，理想情况下，时间复杂度是 $O(logn)$。

不过，二叉查找树在频繁的动态更新过程中，可能会出现树的高度远大于 $lo{g}_{2}n$ 的情况，从而导致哥哥操作的效率下降。极端情况下，二叉树会退化为链表，时间复杂度会退化到 $O(n)$。上篇文章说了，要解决这个复杂度退化的问题，我们需要设计一种平衡二叉树，这也是本章要将的这种数据结构。

很多书籍，但凡讲到平衡二叉查找树，就会拿红黑树作为例子。不仅如此，如果你有一定的开发经验，你会发现，在工程中，很多用到平衡二叉查找树的地方都会用红黑树。你有没有想过，为什么工程中都喜欢用红黑树，而不是其他平衡二叉查找树呢？

---

什么是 “平衡二叉查找树”？

平衡二叉树的严格定义是这样的：二叉树中任意一个结点的左右子树的高度相差不能大于 1。从这个定义来看，上篇文章讲的完全二叉树、满二叉树其实都是平衡二叉树，但是非并完全二叉树也有可能是平衡二叉树。

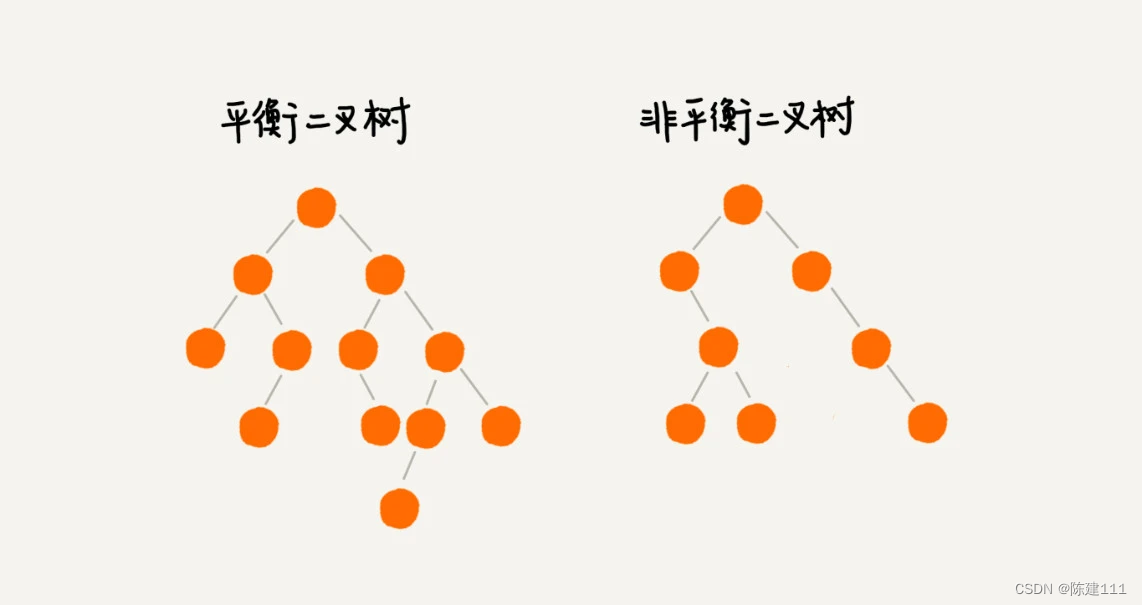
平衡二叉查找树不仅满足上面平衡二叉树的定义，还满足二叉查找树的特点。最先被发明的平衡二叉查找树是 AVL 树，它严格符合刚刚讲到的平衡二叉查找树的定义，即任何子节点的左右子树的高度相差不超过 1，是一种高度平衡的二叉查找树。

但是很多平衡二叉查找树其实并没有严格符合上面的定义，所以，我感觉没必要去死抠定义。对于平衡二叉查找树这个概念，我觉得我们要从这个数据结构的由来，去 “理解” 平衡的意思。

发明平衡二叉查找树这类数据结构的初衷是，解决普通二叉查找树在频繁的插入、删除等动态更新的情况下出现时间复杂度退化的问题。

所以，平衡二叉查找树中 “平衡” 的意思，其实就是让整棵树左右看起来都比较 “对称”、比较 “平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

所以，如果我们现在设计一个新的平衡二叉查找树，只要树的高度不比 $lo{g}_{2}n$ 大很多（比如书的高度仍然是对数量级的），尽管它不符合我们前面的严格的平衡二叉查找树的定义，但我们仍可以说，这是一个合格的平衡二叉查找树。

如何定义一棵 “红黑树”？

平衡二叉查找树其实有很多，比如 Splay Tree（伸展树）、Treap（树堆）等，但是，我们提到平衡二叉查找树，听到的基本都是红黑树。它的出镜率甚至要高于 “平衡二叉查找树” 这几个字，有时候，我们甚至默认平衡二叉查找树就是红黑树，那我们现在就来看看这个 “明星树”。

红黑树的英文是 “Red-Black Tree”，简称 R-B Tree。它是一种不严格的平衡二叉查找树，前面说了，它的定义是不严格符合平衡二叉查找树的定义的。那红黑树的究竟是怎么定义的呢？

顾名思义，红黑树中的节点，一类被标记为红色，一类被标记为红色。此外，一棵红黑树还要满足这样几个要求：

• 根节点是黑色的
• 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不能存储数据
• 任何相邻的节点不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
• 每个节点，从该节点到达其可达的叶子节点的所有路径，都包含相同数目的黑色节点；

这里的第二点要求 “每个叶子节点都是黑色的空节点” ，稍微有些奇怪，它主要是为了简化红黑树的代码实现而设置的，下篇文章我们讲解红黑树的实现时会降到。本章暂时不考虑这一点，所以，在画图和讲解的时候，将黑色的、空的叶子节点都省略掉了。

下面画了两个红黑树的图例，你可以对照看下。

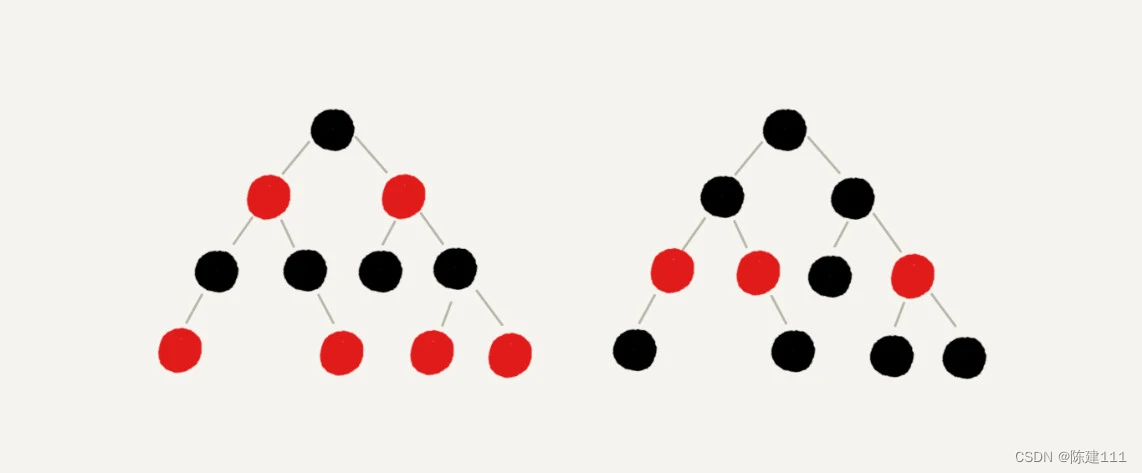
为什么说红黑树都是 “近似平衡” 的？

前面也讲到，平衡二叉查找树的初衷，是为了解决二叉查找树因为动态更新导致的性能退化问题。所以，“平衡” 的意思可以等价为性能不退化。 “近似平衡” 就等价为性能不会退化得太严重。

上篇文章讲过，二叉查找树很多操作的性能都跟树的高度成正比。一棵极其平衡的二叉树（满二叉树或者完全二叉树）的高度大约是 $lo{g}_{2}n$，所以如果要证明红黑树是近似平衡的，我们只需要分析，红黑树的高度是否比较稳定地趋近 $lo{g}_{2}n$ 就好了。

红黑树的高度不是很好分析，我带你一步步来推导。

首先，我们来看，如果我们将红色节点从红黑树中去掉，那单纯包含黑色节点的红黑树的高度是多少呢？

红色节点删除之后，有些节点就没有父节点了，我们会直接拿这些节点的祖父节点（父节点的父节点）作为父节点。所以，之前的二叉树就变成了四叉树。

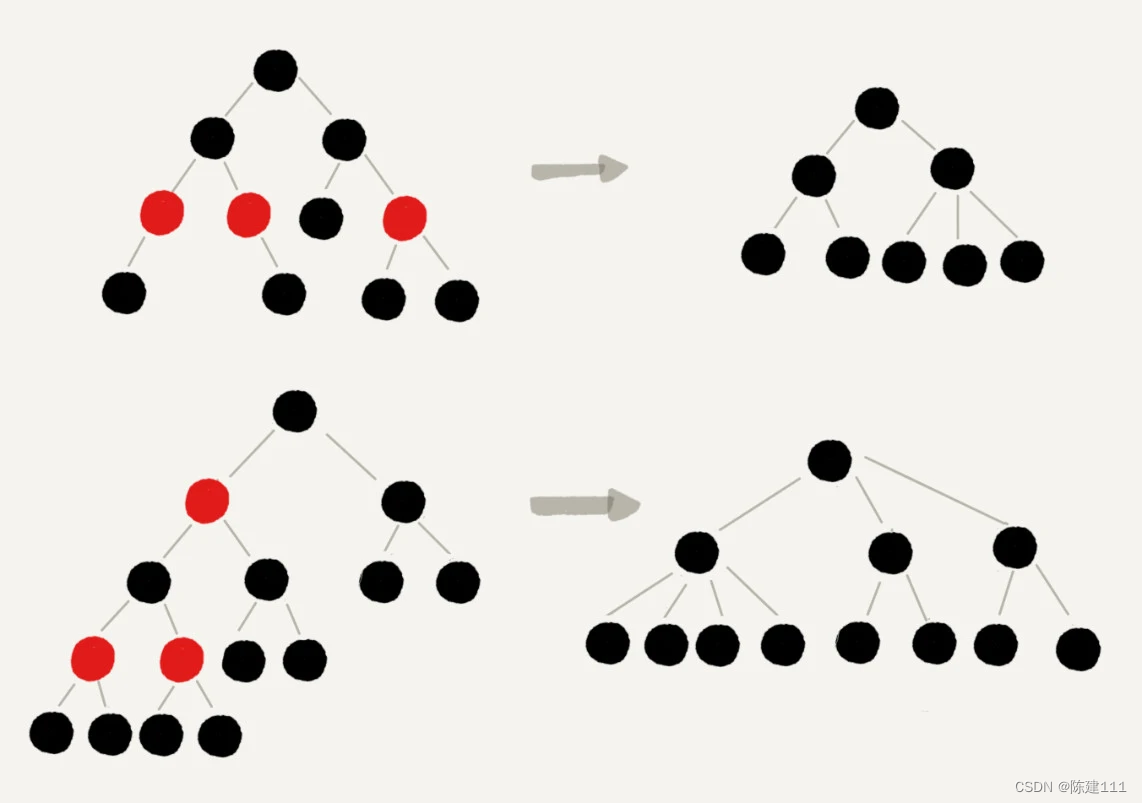
前面红黑树的定义里有这么一条：从任意节点到可达节点的叶子节点的每个路径包含相同数目的黑色节点。我们从四叉树中取出某些节点，放到叶子节点位置，四叉树就变成了完全二叉树。所以，仅包含黑色节点的四叉树的高度，比包含相同节点个数的完全二叉树的高度还要小。

上篇文章我们说，完全二叉树的高度近似 $lo{g}_{2}n$，这里的四叉 “黑树” 的高度要低于完全二叉树，所以去掉红色节点的 “黑树” 的高度也不会超过 $lo{g}_{2}n$。

现在我们知道只包含黑色节点的 “黑树” 的高度，那我们现在把红色节点加回去，高度会变成多少呢？

从上面画的红黑树的例子和定义看，在红黑树中，红色节点不能相邻，也就是说，有一个红色节点就要至少一个黑色节点，将它跟其他红色节点隔开。红黑树中包含最多黑色节点的路径不会超过 $lo{g}_{2}n$，所以加入红色节点之后，最长路径不会超过 $2lo{g}_{2}n$，也就是说，红黑树的高度近似 $2lo{g}_{2}n$。

所以，红黑树的高度之比高度平衡的 AVL 树（$lo{g}_{2}n$）仅仅大了一倍，在性能上，下降得并不多。这样推导出来的结果不够精确，实际上红黑树的性能更好。

为什么工程中都用红黑树这种二叉树？

刚刚提到了很多平衡二叉查找树，现在我们来看下，为什么工程中都用红黑树这种二叉树？

前面提到 Treap、Splay Tree，绝大部分情况下，它们的操作效率都很高，但是也无法避免极端情况下时间复杂度的退化。尽管这种情况出现的概率不大，但是对于单词操作时间非常敏感的场景来说，它们并不适用。

AVL 是一种高度平衡的二叉树，所以查找的效率非常高，但是，有利就有弊，AVL 树为了维持这种高度的平衡，就要付出更多的代价。每次插入、删除都要做调整，就比较复杂、耗时。所以，对于频繁插入、删除操作的集合，使用 AVL 树的代价就有点高了。

红黑树只是做到了近似平衡，并不是严格的平衡，所以在维护平衡的成本上，要比 AVL 树要低。

所以，红黑树的插入、删除、查找各种操作性能都比较稳定。对于工程应用来说，要面对各种异常情况，为了支撑这种工业级的应用，我们更倾向于性能稳定的平衡二叉查找树。

小结

很多同学觉得红黑树很难，的确，它算式最难掌握的一种数据结构。其实红黑树最难的地方是它的实现，在下一章节我们会专门讲解。

不过，我认为，我们其实不应该把学些的侧重点，放到它的实现上。

我们学习数据结构和算法，要学习它的由来、特性、适用场景以及它能解决的问题。对于红黑树，也不例外。你如果能搞懂这几个问题，其实就已经足够了。

红黑树是一种平衡二叉查找树。它是为了解决普通二叉查找树在数据更新的过程中，复杂度退化的问题而产生的。红黑树的高度近似 $lo{g}_{2}n$，所以它是近似平衡，插入、删除、查找操作的时间复杂度都是 $O(logn)$。

因为红黑树是一种性能非常稳定的二叉查找树，所以，在工程中，但凡是用到动态插入、删除、查找数据的场景，都可以用到它。不过，它实现起来比较复杂，如果自己写代码实现，难度会有些高，这个时候，我们其实更倾向于用跳表来替代它。