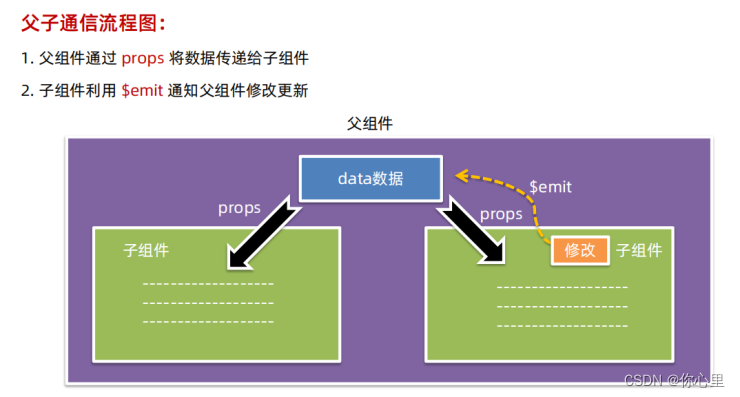
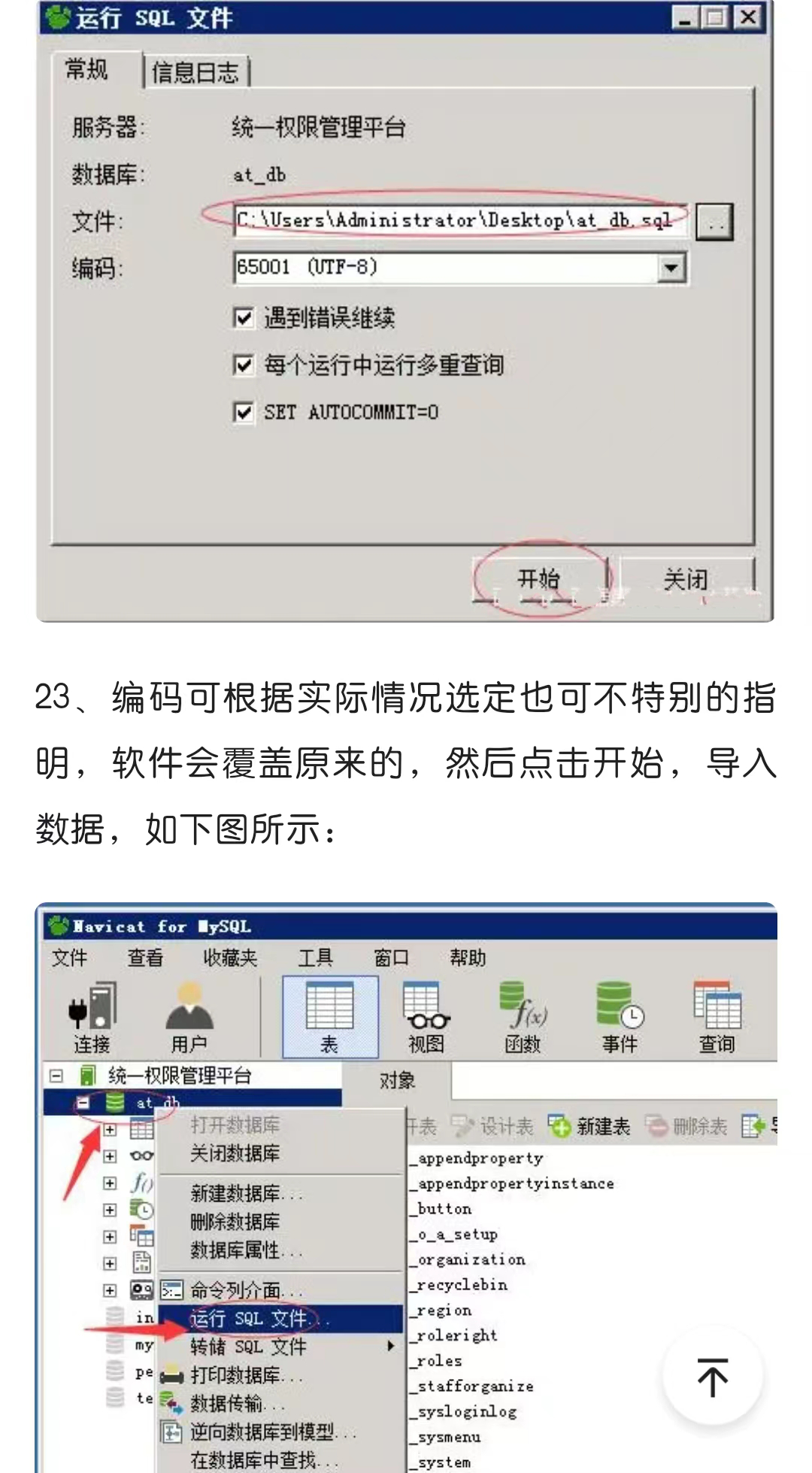
排序力扣题
一:合并区间
56. 合并区间
方法一:先排序再合并
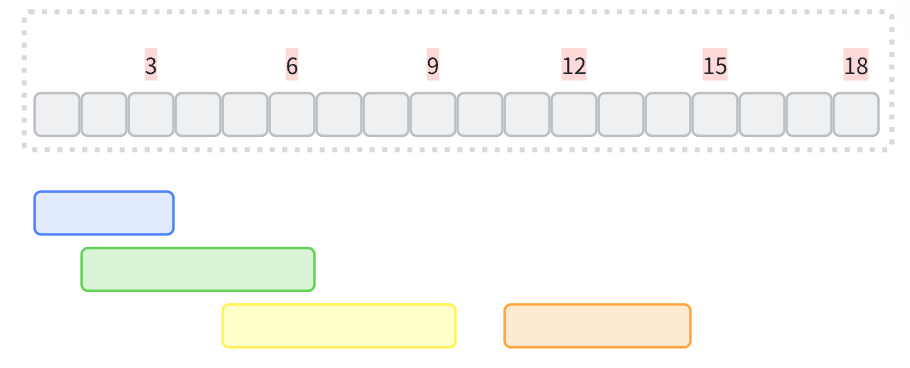
如图,把区间按照起点从小到达排序,如果起点相同那么按照终点小的优先排序
然后每次记录一个区间,访问下一个区间:
- 如果下一个区间的起点<=前一个区间的终点,那么把前一个区间终点进行更新,选择两个区间最大的
- 如果下一个区间起点>前一个区间终点,说明断开了,把更新后的区间放入结果
vector<vector<int>> merge(vector<vector<int>>& intervals) {
//首先对interval排序
sort(intervals.begin(),intervals.end(),\
[](vector<int>& a,vector<int>& b){
return a[0]<b[0] || (a[0]==b[0]&&a[1]<b[1]);
});
//初始化区间为-1
int left=-1;
int right=-1;
vector<vector<int>> res;
for(auto& val:intervals){
int start=val[0];
int end=val[1];
if(start<=right){//区间起点<=上一个区间终点
right=max(right,end);
}else{
//区间存入结果
if(left!=-1){
res.push_back({left,right});
}
//更新区间
left=start;
right=end;
}
}
//最后一个区间存入结果
if(left!=-1){
res.push_back({left,right});
}
return res;
}
当然也可以在
res无内容或者存放的末尾的终点<当前区间起点时候存结果vector<vector<int>> res; for(auto& val:intervals){ int start=val[0]; int end=val[1]; if(res.size()==0 || res.back()[1]<start){ res.push_back({start,end}); }else{ res.back()[1]=max(end,res.back()[1]); } } return res;
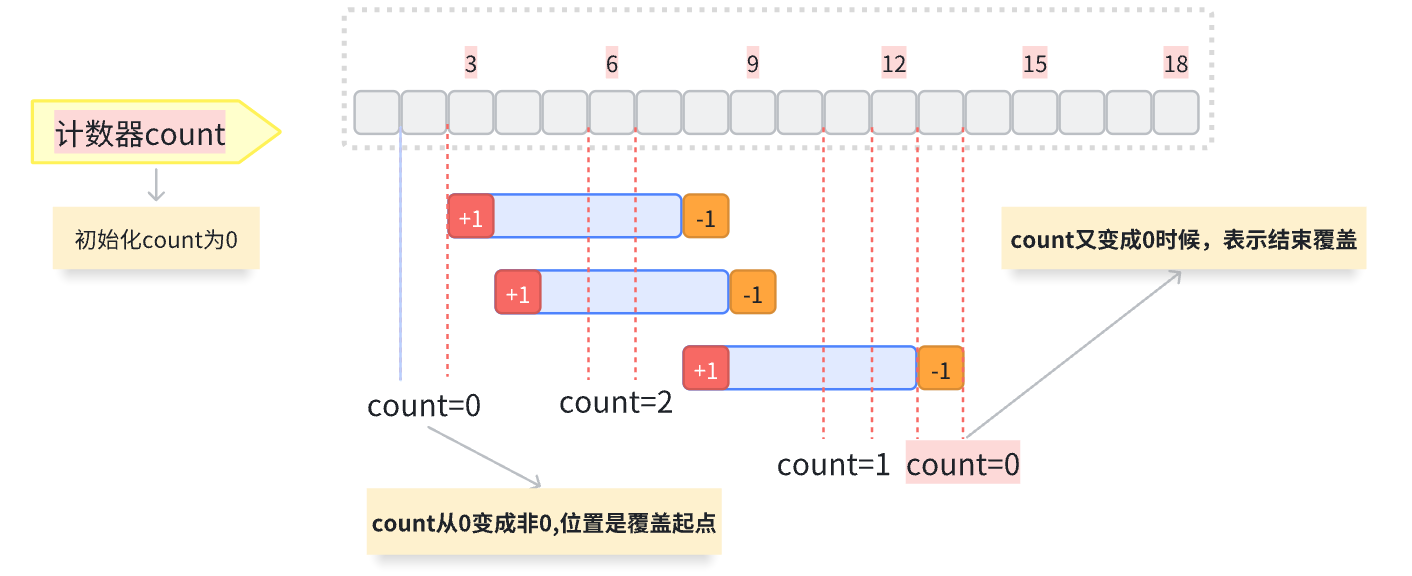
方法二:差分
定义一个事件二元组:event
- 事件的起点:event {区间值,
+1}- 事件的终点:event{区间值+1,
-1}
所以count从0->正数->0,恰好是求的一个区间
vector<vector<int>> merge(vector<vector<int>>& intervals) {
//定义事件
vector<pair<int,int>> event;
for(auto& val:intervals){
event.push_back({val[0],1});
event.push_back({val[1]+1,-1});
}
//排序
sort(event.begin(),event.end());
//计数
int count=0;
int start=-1;
vector<vector<int>> ans;
for(auto& val:event){
if(count==0)//第一个0:记录起点
start=val.first;
count+=val.second;
if(count==0)//又变成0:成为终点
ans.push_back({start,val.first-1});
}
return ans;
}
当然也可以直接区间起点+1,区间终点-1,只是需要自定义排序
vector<vector<int>> merge(vector<vector<int>>& intervals) { //定义事件,这里记录:{起点,+1},{终点,-1} vector<pair<int,int>> events; for(auto& val:intervals){ events.push_back({val[0],+1}); events.push_back({val[1],-1}); } //排序 sort(events.begin(),events.end(),\ [](pair<int,int>& a,pair<int,int>& b){ return a.first<b.first ||a.first==b.first && a.second>b.second; }); //开始遍历evevt int count=0; int start=-1; vector<vector<int>> ans; for(auto& eve:events){ if(count==0){ start=eve.first; } count+=eve.second; if(count==0){ ans.push_back({start,eve.first}); } } return ans; }自定义函数也可以写成仿函数:
class cmp { public: bool operator()(pair<int, int>& e1, pair<int, int>& e2) { if (e1.first == e2.first) return e1.second > e2.second; return e1.first < e2.first; } // 排序 sort(events.begin(), events.end(), cmp());
二:翻转对
493. 翻转对
思路:
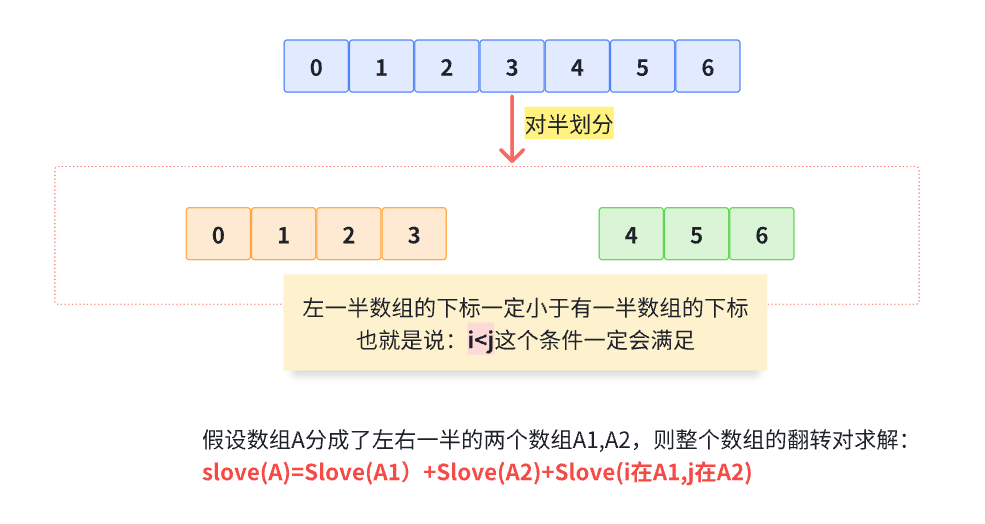
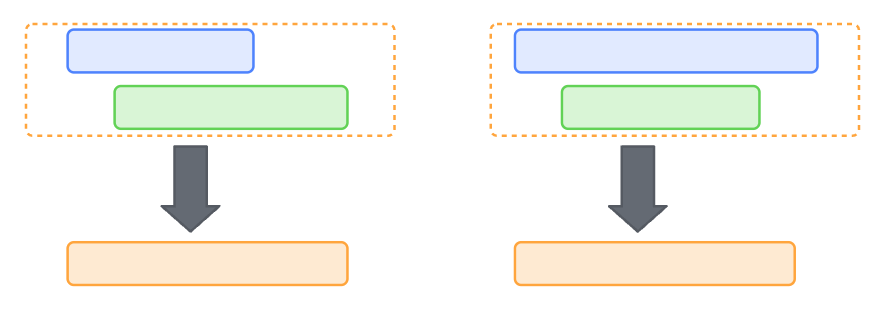
递归地对数组进行左右两部分的划分,直至数组长度为1时就结束递归。
这样天然的满足i<j的条件,因为i在左一半数组,j在右一半数组
为了能够使得求逆序对更容易,在合并时候进行排序,然后不断累积求的结果。
遍历一次左一半数组,每次第一个不满足的j值,之前就是符合要求的。
所以整个过程和分治排序一样,只不过要在合并前统计一次翻转对的个数
统计翻转对的时机:
在得到左右有序序列之后,合并左右有序序列之前。
分治算法的步骤就是:
分割+求解+合并
分治排序过程:
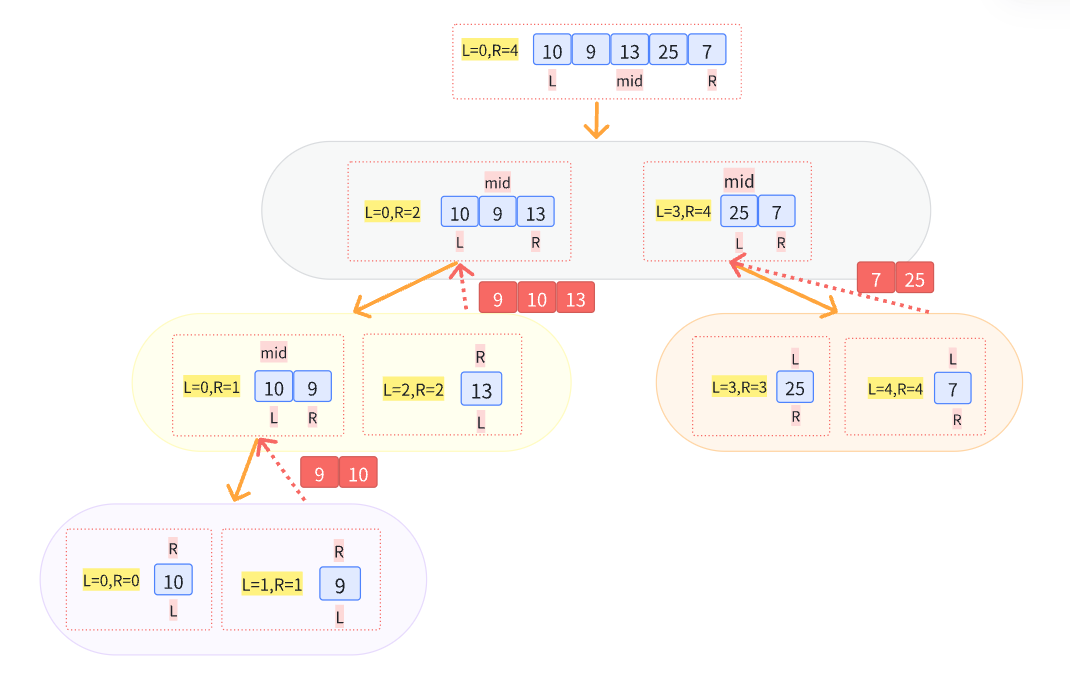
解法一:
class Solution {
public:
int reversePairs(vector<int>& nums) {
mergeSort(nums,0,nums.size()-1);
for(auto& val: nums){
cout<<val<<" ";
}
return ans;
}
private:
int ans=0;
void merge(vector<int>& nums,int l,int mid,int r){
int i=l;
int j=mid+1;
int* aux=new int[r-l+1];
//[l,r]~[0,r-l]
for(int k=0;k<r-l+1;k++){
if(i>mid){
aux[k]=nums[j++];
}else if(j>r){
aux[k]=nums[i++];
}else if(nums[i]<nums[j]){
aux[k]=nums[i++];
}else{
aux[k]=nums[j++];
}
}
//赋值回nums
for(int i=l;i<=r;i++){
nums[i]=aux[i-l];
}
}
void mergeSort(vector<int>& nums,int l,int r){
if(l==r) return;
int mid=(l+r)>>1;
//对半划分
mergeSort(nums,l,mid);
mergeSort(nums,mid+1,r);
//统计翻转对个数
int j=mid+1;
for(int i=l;i<=mid;i++){
while(j<=r && (long)nums[i]>(long)2*nums[j]) j++;
//[mid+1,j-1]是符合要求的
ans+=j-mid-1;
}
//合并排序
merge(nums,l,mid,r);
}
};
把统计个数放在合并还原的函数也可以
int ans=0;
void merge(vector<int>& nums,int l,int mid,int r){
int i=l;
int j=mid+1;
int* aux=new int[r-l+1];
//统计翻转对个数
for(int i=l;i<=mid;i++){
while(j<=r && (long)nums[i]>(long)2*nums[j]) j++;
//[mid+1,j-1]是符合要求的
ans+=j-mid-1;
}
//把i,j值还原
i=l;
j=mid+1;
int k=0;
//[l,r]~[0,r-l]
while(i<=mid && j<=r){
if(nums[i]<nums[j]){
aux[k++]=nums[i++];
}else{
aux[k++]=nums[j++];
}
}
while(i<=mid){
aux[k++]=nums[i++];
}
while(j<=r){
aux[k++]=nums[j++];
}
//赋值回nums
for(int i=0;i<r-l+1;i++){
nums[i+l]=aux[i];
}
}
void mergeSort(vector<int>& nums,int l,int r){
if(l==r) return;
int mid=(l+r)>>1;
//对半划分
mergeSort(nums,l,mid);
mergeSort(nums,mid+1,r);
//合并排序
merge(nums,l,mid,r);
}
贪心算法(Greedy Algorithm)
对于一道题,要优先考虑
分治,搜索,动态规划等基于全局考虑的算法,如果它们时间复杂度比较高,再去考虑能否利用贪心求解。贪心算法的难点在于:证明这道题可以利用贪心去求解
贪心算法是一种:
- 每一步选择当前状态下的最优决策
也就是求:局部最优解
- 然后希望每次局部最优的最终结果也是全局最优
通过每次局部最优达到求全局最优的目的
贪心与搜索和动态规划的区别
- 贪心不对整个状态空间进行遍历或计算,而是始终按照局部最优选择执行下去,不会回头
因为局部最优并不一定会得到全局最优,所以需要证明:本题每次局部最优可以得到全局最优
- 能利用贪心求解的题目也可以利用搜索和动态规划求解,但是贪心一定是最高效的
贪心算法:
- 不从整体最优上加以考虑,一步一步进行,每一步只以当前情况为基础,根据某个优化测度做出局部最优选择。
- 省去了为找到最优解要穷举所有可能所必须耗费的大量时间
贪心算法特征
能用贪心算法解决的问题必须满足下面的两个特征:
- 贪⼼选择性质
一个问题的全局最优解可以通过一系列局部最优解来得到
贪心算法在进行选择时,可能会依赖
之前做出的选择,但不会依赖任何将来的选择或是子问题的解贪心算法解决的问题在程序的运行过程中无回溯过程
- 最优子结构
最优子结构性质:指的是一个问题的最优解包含其子问题的最优解
问题的最优子结构性质是该问题能否用贪心算法求解的关键
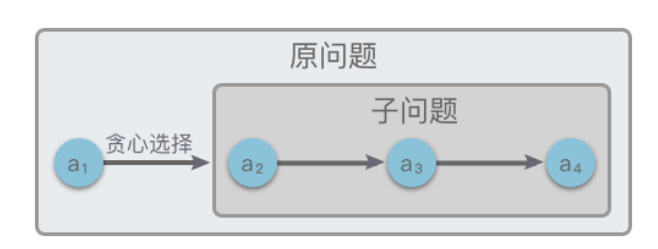
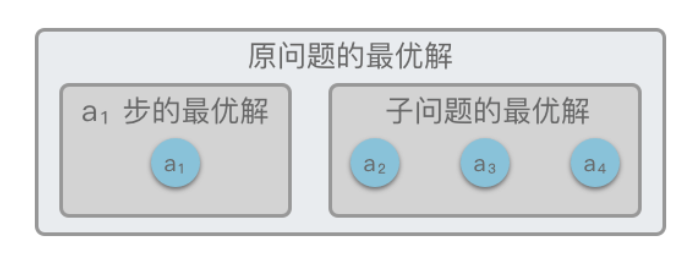
如果原问题 𝑆 的最优解=「第 𝑎1 步通过贪心选择的局部最优解」+「 子问题𝑆子问题 的最优解」.则说明该问题满足最优子结构性质。
- 如果不能利用子问题的最优解推导出整个问题的最优解,那么这种问题就不具有最优子结构
力扣题—贪心
一:分饼干
455. 分发饼干
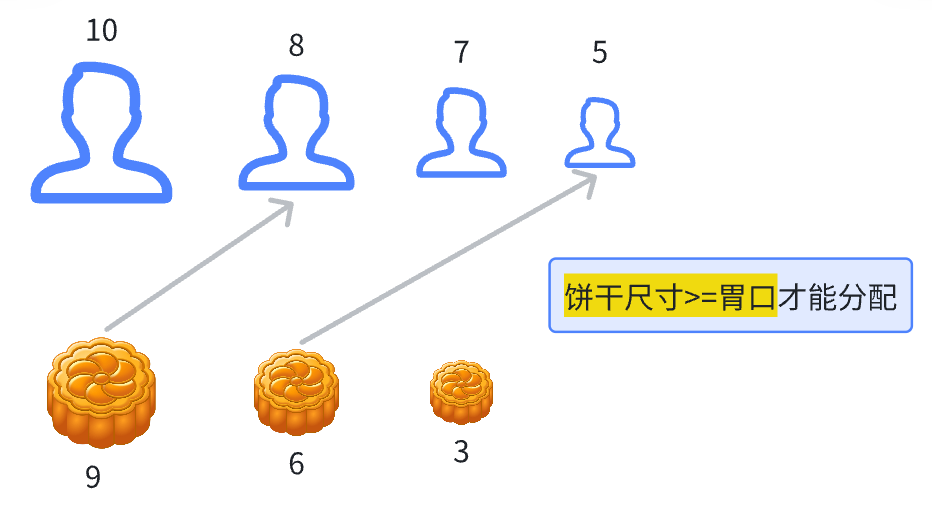
解法一:大饼干分给大孩子
把孩子和饼干按照升序排序,然后遍历孩子,如果孩子胃口值<=当前大饼干,就把饼干分配给他
不然的话,:也就是饼干小于胃口,放弃当前孩子,寻找下一个更小的孩子
int findContentChildren(vector<int>& g, vector<int>& s) {
//每个孩子i有胃口值g[i]
//每个饼干j有尺寸值s[j]
//目标:尽可能的满足孩子多
int j=0;
int col=0;
//降序排序
sort(g.begin(),g.end(),greater<int>());
sort(s.begin(),s.end(),greater<int>());
//遍历胃口,优先把大饼干给大胃口
for(int i=0;i<g.size() && j<s.size();i++){
if(g[i]<=s[j]){//分配饼干
col++;
j++;
}
}
return col;
}
循环条件还可以:
-
for(int i=0;i<g.size();i++){ if(j<s.size() && s[j]>=g[i]){ //饼干可以分给当前孩子 col++; j++; } } -
for(int i=0;i<g.size();i++){ if(j==s.size()) break; if(s[j]>=g[i]){ //饼干可以分给当前孩子 col++; j++; } } -
int i=0,j=0; int col=0; //遍历孩子分饼干 while(i<g.size() && j<s.size()){ if(s[j]>=g[i]){ i++; j++; col++; }else{//放弃孩子 i++; } }
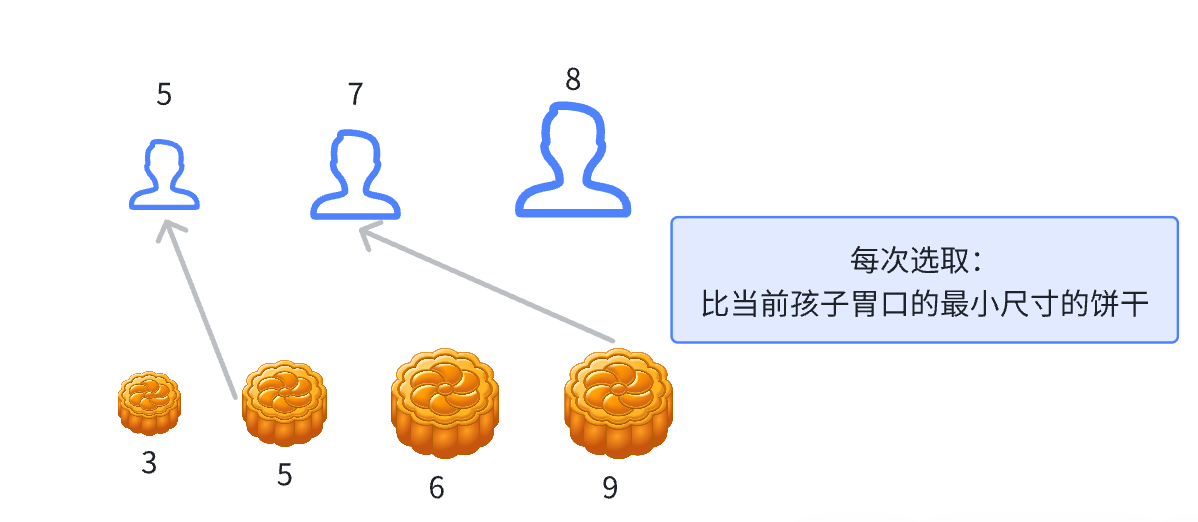
方法二:小饼干分给小孩子
这种情况是,遍历到下一个孩子之前,需要不断放弃尺寸小饼干,直至找到满足当前孩子胃口饼干后,接着遍历
int findContentChildren(vector<int>& g, vector<int>& s) {
//每一个孩子i有胃口g[i]
//每一块饼干j有尺寸s[j]
/*孩子和饼干升序排序*/
sort(g.begin(),g.end());
sort(s.begin(),s.end());
//遍历孩子
int j=0;
int col=0;
for(int i=0;i<g.size();i++){
//遍历饼干,找到一个最小的满足胃口
while(j<s.size() && s[j]<g[i]) j++;
if(j<s.size()){
//找到了
j++;
col++;
}
}
return col;
}
总结:
小饼干分给小孩子,相当于放弃饼干
因为最小饼干不能给小孩子,一定也不能给其他孩子
大饼干分给大孩子,相当于放弃孩子
因为大饼干肯定会被孩子吃,所以优先满足大胃口
二:买卖股票
122. 买卖股票的最佳时机 II
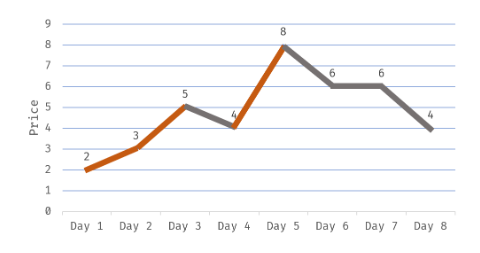
这里同一天既可以买股票,也可以卖股票,还可以买卖同时进行
如图:后一天比前一天大就累计利润,相当于前一天买后一天卖;后一天比前一天小就跳过
int maxProfit(vector<int>& prices) {
int profit=0;
for(int i=1;i<prices.size();i++){
profit+=max(0,prices[i]-prices[i-1]);
}
return profit;
}
三:跳跃游戏
45. 跳跃游戏 II
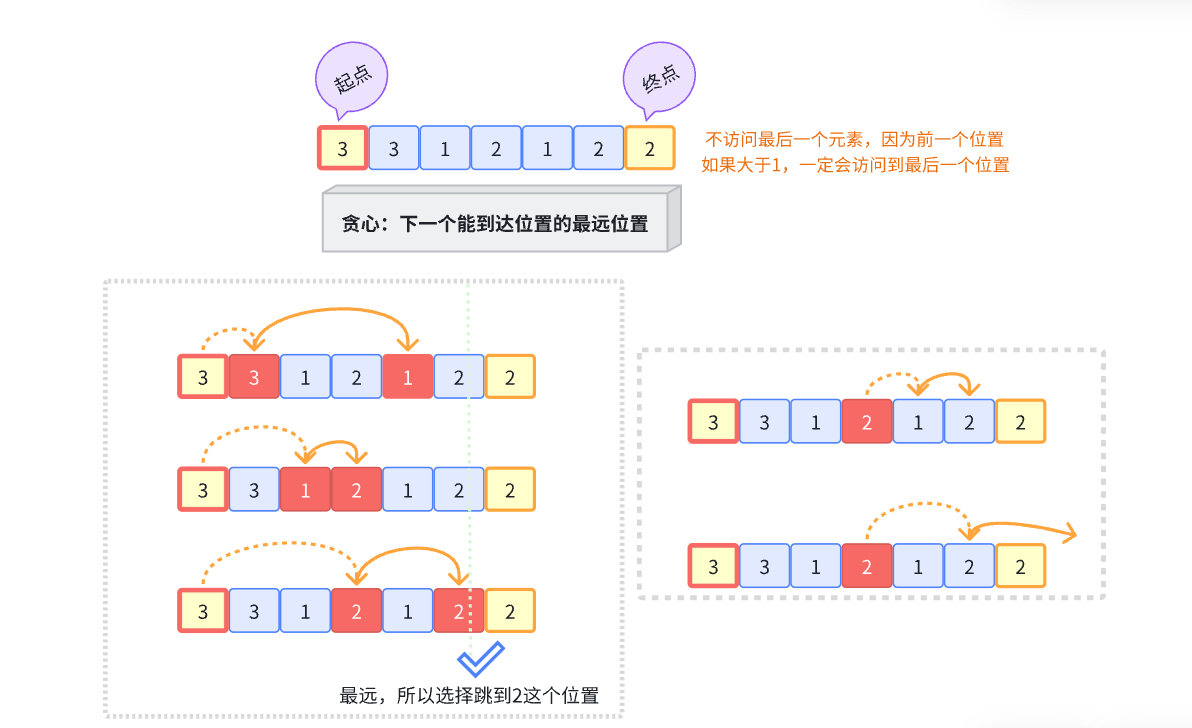
分析:假设当前位置为index,而且该位置可以跳的最大距离为:nums[index]
则:枚举1~nums[index]的所有可能,然后选择到达位置后,下一个位置的最远距离
也就是说:如果到达的位置能达到的下一个位置最远,就选该位置
int jump(vector<int>& nums) {
int n=nums.size();
int curPos=0;
int step=0;//跳跃次数
while(curPos < n-1){//不到达最后位置
// 当前位置的跳跃步数为0,到达不了
if(nums[curPos]==0) return -1;
//枚举位置终点
int right=curPos+nums[curPos];
//如果直接能超过终点,直接return
if(right>=n-1) return step+1;
int nextPos=curPos+1;
for(int i=curpos+2;i<=right;i++){
if(i+nums[i]>nextPos+nums[nextPos])
nextPos=i;
}
//选择该位置,步数+1
curPos=nextPos;
step++;
}
return step;
}
方法二:
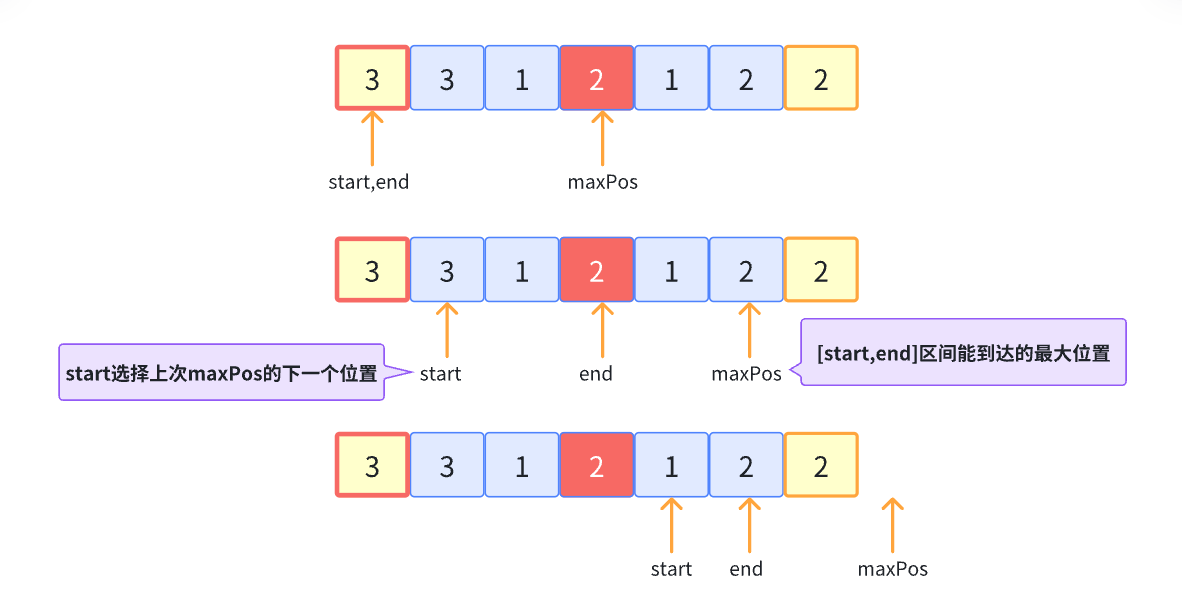
将start和end初始化在第一个位置,然后计算可到达的最远距离maxPos
每次:start等于上一个end+1,end选择maxPos,其实这就是遍历每一个位置取最大
int jump(vector<int>& nums) {
//start和end初始化第一个位置
int start=0,end=0;
int ans=0;//返回结果
while(end < nums.size()-1){
int maxPos=0;
for(int i=start;i<=end;i++){
maxPos=max(maxPos,i+nums[i]);
}
//更新位置
start=end+1;
end=maxPos;
ans++;//跳了一次
}
return ans;
}
上述代码可以优化
- 可以在i==end统计次数
for (int i = start; i < nums.size() - 1; i++) { maxPos = max(maxPos, i + nums[i]); //因为i从头遍历到最后,所以==end时候,步数+1 if (i == end) { start = end + 1; end = maxPos; ans++; } }
- 可以没有起点
区间遍历[start,end],start每次更细为end+1,所以相当于从0依次遍历
for (int i = 0; i < nums.size() - 1; i++) { maxPos = max(maxPos, i + nums[i]); //因为i从头遍历到最后,所以==end时候,步数+1 if (i == end) { end = maxPos; ans++; } }https://leetcode.cn/problems/minimum-initial-energy-to-finish-tasks/)