DeepSORT（目标跟踪算法）中的马氏距离详解（很详细）

flyfish

马氏距离的公式是由印度统计学家【普拉萨纳·钱德拉·马哈拉诺比斯（Prasanta Chandra Mahalanobis）】）（好长的名字，抄的）在1936年提出的。马氏距离是一种多维尺度上的距离度量，它考虑了各个维度之间的相关性，并且通过协方差矩阵对数据进行缩放，使得在计算不同数据点之间的距离时，可以考虑到各个维度的不同特性。可以直接拖到最后的一张图，看下马氏距离与欧式距离相比有什么优势

介绍

假设我们有两个点 $x$ 和 $y$ ，并且我们有这些点的协方差矩阵 $S$ 。马氏距离的公式为：

$D_M(x, y) = \sqrt{(x - y)^T S^{-1} (x - y)}$

下面是一个具体的例子：

假设点 $x = [2, 3]$ ，点 $y = [6, 8]$ ，协方差矩阵 $\begin{bmatrix} 4 & 2 \\ 2 & 3 \end{bmatrix}$ 。

代码计算

计算 $x - y$
计算协方差矩阵的逆矩阵 $S^{-1}$
计算 $x - y)^T S^{-1} (x - y)$
最后取平方根得到马氏距离
让我们用Python代码验证这个计算过程。

代码

import numpy as np

# 定义点 x 和 y
x = np.array([2, 3])
y = np.array([6, 8])

# 定义协方差矩阵 S
S = np.array([[4, 2],
              [2, 3]])

# 计算 x - y
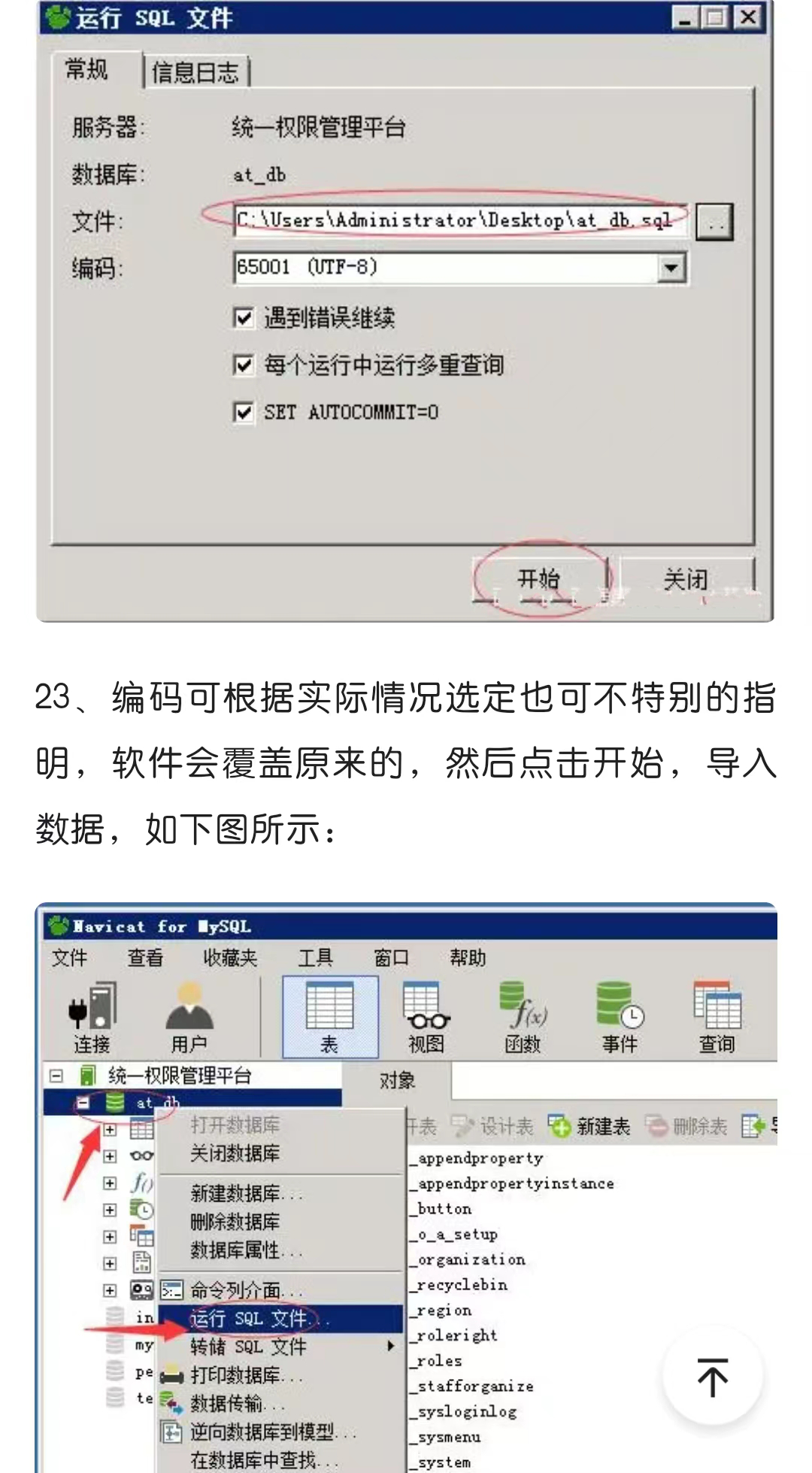
delta = x - y

# 计算协方差矩阵的逆矩阵 S^{-1}
S_inv = np.linalg.inv(S)

# 计算马氏距离
mahalanobis_distance = np.sqrt(np.dot(np.dot(delta.T, S_inv), delta))

print(mahalanobis_distance)

我们来执行这个代码，看看结果。

2.9154759474226504

计算结果显示，点 $x$ 和 $y$ 之间的马氏距离为 2.915。

手工计算马氏距离

计算 $x - y$
计算协方差矩阵的逆矩阵 $S^{-1}$
计算 $x - y)^T S^{-1} (x - y)$
最后取平方根得到马氏距离
给定点 $x = [2, 3]$ 和 $y = [6, 8]$ ，以及协方差矩阵 $\begin{bmatrix} 4 & 2 \\ 2 & 3 \end{bmatrix}$ 。

步骤 1: 计算 $x - y$

$\delta = x - y = [2, 3] - [6, 8] = [-4, -5]$

步骤 2: 计算协方差矩阵的逆矩阵 $S^{-1}$

计算 $S$ 的行列式：
$\det(S) = 4 \cdot 3 - 2 \cdot 2 = 12 - 4 = 8$

计算伴随矩阵：
$\text{adj}(S) = \begin{bmatrix} 3 & -2 \\ -2 & 4 \end{bmatrix}$

计算逆矩阵：
$S^{-1} = \frac{1}{8} \cdot \text{adj}(S) = \frac{1}{8} \cdot \begin{bmatrix} 3 & -2 \\ -2 & 4 \end{bmatrix} = \begin{bmatrix} 0.375 & -0.25 \\ -0.25 & 0.5 \end{bmatrix}$

步骤 3: 计算 $x - y)^T S^{-1} (x - y)$

我们分步计算：

计算 $S^{-1} \cdot \delta^T$ ：
$S^{-1} \cdot \delta^T = \begin{bmatrix} 0.375 & -0.25 \\ -0.25 & 0.5 \end{bmatrix} \cdot [-4, -5]^T$
我们先计算每个元素：
$\begin{align*} 0.375 \cdot (-4) + (-0.25) \cdot (-5) &= -1.5 + 1.25 = -0.25 \\ -0.25 \cdot (-4) + 0.5 \cdot (-5) &= 1 - 2.5 = -1.5 \\ \end{align*}$
所以：
$S^{-1} \cdot \delta^T = [-0.25, -1.5]$
计算 $\delta \cdot [-0.25, -1.5]^T$ ：
$\delta \cdot [-0.25, -1.5]^T = [-4, -5] \cdot [-0.25, -1.5]^T = (-4 \cdot -0.25) + (-5 \cdot -1.5) = 1 + 7.5 = 8.5$

步骤 4: 取平方根

$\sqrt{8.5} \approx 2.915$

马氏距离的绘图

绘制两个点之间的欧氏距离和马氏距离来进行比较。假设我们使用之前定义的点 $x = [2, 3]$ 和 $y = [6, 8]$ ，以及协方差矩阵 $S$ 。

我们可以进行以下步骤：

计算欧氏距离。
计算马氏距离。
绘制这两个点在平面上的位置。
绘制欧氏距离和马氏距离的线段。
以下是完整的Python代码来实现这些步骤，并进行绘图。

import numpy as np
import matplotlib.pyplot as plt

# 定义点 x 和 y
x = np.array([2, 3])
y = np.array([6, 8])

# 定义协方差矩阵 S
S = np.array([[4, 2],
              [2, 3]])

# 计算欧氏距离
euclidean_distance = np.linalg.norm(x - y)

# 计算马氏距离
delta = x - y
S_inv = np.linalg.inv(S)
mahalanobis_distance = np.sqrt(np.dot(np.dot(delta.T, S_inv), delta))

# 绘图
plt.figure(figsize=(8, 8))
plt.scatter(*x, color='blue', label='Point x')
plt.scatter(*y, color='red', label='Point y')

# 绘制欧氏距离
plt.plot([x[0], y[0]], [x[1], y[1]], 'k--', label=f'Euclidean Distance = {euclidean_distance:.2f}')

# 为了绘制马氏距离的等高线，我们可以绘制马氏距离的椭圆
from matplotlib.patches import Ellipse

# 计算椭圆的参数
eigvals, eigvecs = np.linalg.eigh(S)
angle = np.degrees(np.arctan2(*eigvecs[:,0][::-1]))

width, height = 2 * np.sqrt(eigvals)

ellipse = Ellipse(xy=x, width=width, height=height, angle=angle, edgecolor='purple', fc='None', lw=2, label=f'Mahalanobis Distance = {mahalanobis_distance:.2f}')
plt.gca().add_patch(ellipse)

plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.title('Comparison of Euclidean and Mahalanobis Distances')
plt.grid(True)
plt.axis('equal')
plt.show()

在这里插入图片描述
欧氏距离和马氏距离的比较：

蓝点代表点 $x$ 。
红点代表点 $y$ 。
虚线表示两点之间的欧氏距离，长度为 6.40。
紫色椭圆表示马氏距离等高线，马氏距离为 2.92。

图中的椭圆反映了协方差矩阵 $S$ 的影响，显示了在不同方向上的不同尺度，这使得马氏距离能更准确地反映点与点之间的关系。欧氏距离忽略了数据的相关性和尺度，而马氏距离考虑了这些因素，使其在一些应用场景中更有用。

协方差

import numpy as np

# 定义数据样本
data = np.array([
    [2, 3],
    [6, 8],
    [3, 5]
])

# 计算均值向量
mean_vector = np.mean(data, axis=0)

# 计算协方差矩阵
cov_matrix = np.cov(data, rowvar=False)

print(mean_vector, cov_matrix)
[3.66666667 5.33333333] [[4.33333333 5.16666667]
 [5.16666667 6.33333333]]

手工计算详细步骤

给定数据样本：

$\text{样本1} = [2, 3]$
$\text{样本2} = [6, 8]$
$\text{样本3} = [3, 5]$

计算均值向量：

$S_{ij} = \frac{1}{n-1} \sum_{k=1}^{n} (x_{ki} - \mu_i)(x_{kj} - \mu_j)$
$\mu = \left[ \frac{2+6+3}{3}, \frac{3+8+5}{3} \right] = [3.67, 5.33]$

计算协方差矩阵

计算 $S_{11}$ ：

$S_{11} = \frac{1}{n-1} \sum_{k=1}^{n} (x_{k1} - \mu_1)^2$ S11

$\begin{aligned}S_{11} &= \frac{1}{2} \left[ (2 - 3.67)^2 + (6 - 3.67)^2 + (3 - 3.67)^2 \right] \\ &= \frac{1}{2} \left[ (-1.67)^2 + (2.33)^2 + (-0.67)^2 \right] \\ &= \frac{1}{2} \left[ 2.79 + 5.43 + 0.45 \right] \\ &= \frac{8.67}{2} = 4.33 \\ \end{aligned}$

计算 $S_{12}$ ：

$S_{12} = \frac{1}{n-1} \sum_{k=1}^{n} (x_{k1} - \mu_1)(x_{k2} - \mu_2)$
$\begin{aligned} S_{12} &= \frac{1}{2} \left[ (2 - 3.67)(3 - 5.33) + (6 - 3.67)(8 - 5.33) + (3 - 3.67)(5 - 5.33) \right] \\ &= \frac{1}{2} \left[ (-1.67)(-2.33) + (2.33)(2.67) + (-0.67)(-0.33) \right] \\ &= \frac{1}{2} \left[ 3.89 + 6.22 + 0.22 \right] \\ &= \frac{10.33}{2} = 5.17 \\ \end{aligned}$
4. 计算 $S_{22}$ ：
$S_{22} = \frac{1}{n-1} \sum_{k=1}^{n} (x_{k2} - \mu_2)^2$
$\begin{aligned} S_{22} &= \frac{1}{2} \left[ (3 - 5.33)^2 + (8 - 5.33)^2 + (5 - 5.33)^2 \right] \\ &= \frac{1}{2} \left[ (-2.33)^2 + (2.67)^2 + (-0.33)^2 \right] \\ &= \frac{1}{2} \left[ 5.43 + 7.11 + 0.11 \right] \\ &= \frac{12.65}{2} = 6.33 \\ \end{aligned}$

协方差矩阵

$\begin{bmatrix} 4.33 & 5.17 \\ 5.17 & 6.33 \end{bmatrix}$

协方差矩阵对称性的解释

协方差矩阵的对称性来源于协方差的定义。对于随机变量 $X$ 和 $Y$ ，协方差定义为：

$\text{Cov}(X, Y) = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \mu_X)(Y_i - \mu_Y)$

由于协方差的计算中 $(X_i - \mu_X)$ 和 $(Y_i - \mu_Y)$ 可以互换位置，所以协方差矩阵的 $i, j$ 元素等于 $j, i$ 元素，即 $\text{Cov}(X, Y) = \text{Cov}(Y, X)$ 。因此协方差矩阵是对称矩阵。

协方差矩阵是对称的。这意味着 $S_{ij}$ 等于 $S_{ji}$ 。矩阵中的元素 $5.17$ 是重复的。

马氏距离公式的推导

马氏距离 $D_M$ 的公式如下：

$D_M = \sqrt{(x - y)^T S^{-1} (x - y)}$

其中：

$x$ 和 $y$ 是两个 $d$ 维向量，表示两个数据点。
$S$ 是数据的协方差矩阵。
$S^{-1}$ 是协方差矩阵 $S$ 的逆矩阵。
$x - y)^T$ 是 $x - y$ 的转置向量。

推导过程

欧氏距离的局限性：在多维数据中，直接使用欧氏距离来度量两个点之间的距离，会忽略各个维度之间的相关性和尺度差异。欧氏距离公式为：
$D_E = \sqrt{(x - y)^T (x - y)}$
标准化：为了克服欧氏距离的局限性，我们需要对数据进行标准化。对于一个维度上的数据，可以用均值和标准差来标准化，得到标准化后的数据：
$\frac{x - \mu}{\sigma}$
考虑相关性：在多维数据中，不同维度之间可能存在相关性。协方差矩阵 $S$ 反映了这种相关性。为了同时考虑尺度和相关性，我们可以对数据点进行变换，使得变换后的数据具有单位方差和零协方差。
变换数据：为了进行这种变换，我们需要使用协方差矩阵的逆矩阵 $S^{-1}$ 来对数据进行缩放。变换后的数据点为：
$z = S^{-1/2} (x - y)$
其中 $S^{-1/2}$ 是协方差矩阵的逆矩阵的平方根。
计算距离：变换后的数据点 $z$ 在单位方差和零协方差的情况下，可以直接使用欧氏距离来度量：
$D_M = \sqrt{z^T z} = \sqrt{(x - y)^T S^{-1} (x - y)}$

上面已经计算的过程再走一遍（温习，下面的可不看）

假设我们有两个数据点 $x = [2, 3]$ 和 $y = [6, 8]$ ，协方差矩阵 $\begin{bmatrix} 4 & 2 \\ 2 & 3 \end{bmatrix}$ ，我们可以计算马氏距离如下：

计算 $x - y$ ：
$\delta = x - y = [2, 3] - [6, 8] = [-4, -5]$
计算协方差矩阵的逆矩阵 $S^{-1}$ ：
$S^{-1} = \begin{bmatrix} 0.6 & -0.4 \\ -0.4 & 0.8 \end{bmatrix}$
计算 $x - y)^T S^{-1} (x - y)$ ：
$\delta^T S^{-1} \delta = [-4, -5] \begin{bmatrix} 0.6 & -0.4 \\ -0.4 & 0.8 \end{bmatrix} \begin{bmatrix} -4 \\ -5 \end{bmatrix} = [4.4 + 2, 2 + 8]$
$\begin{bmatrix} -4 & -5 \end{bmatrix} \begin{bmatrix} -0.8 \\ -1.5 \end{bmatrix} = 3.2 + 7.5 = 8.5$
最后取平方根：
$D_M = \sqrt{8.5} \approx 2.915$
通过这种方式，我们可以考虑各个维度之间的相关性和不同的尺度，得到更准确的点与点之间的距离度量。