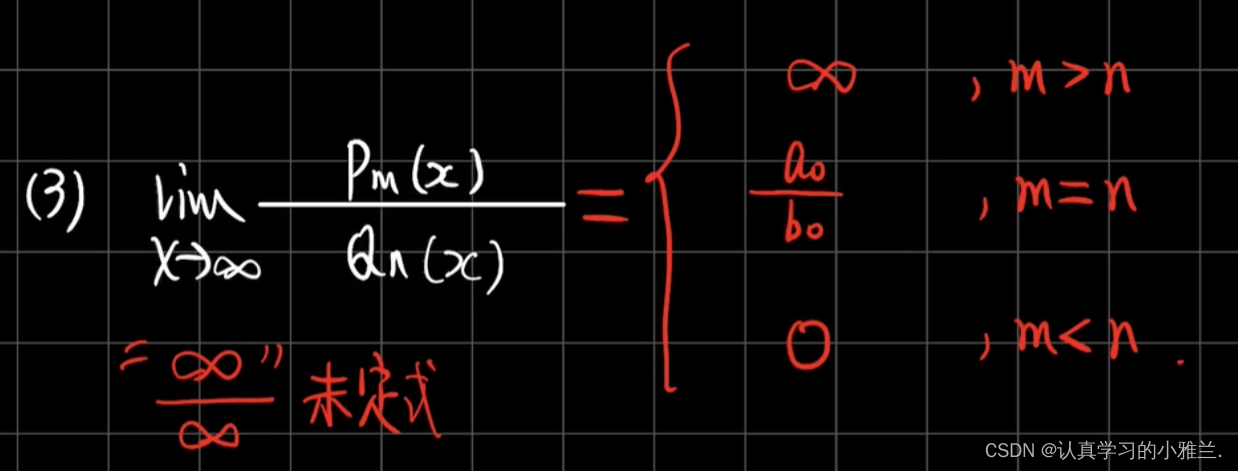参考代码:None
1. 概述
介绍:这篇文章提出的方法是对LSS中深度估计部分进行改进,其改进的点是在深度估计部分引入立体匹配去估计周视相机下的深度信息,其中立体匹配使用前后视频帧进行构建(可以看作是时序信息的使用,只不过只有两帧信息)。此外,引入DORN中的深度采样策略(SID,Spacing-Increasing Discretization)使得近处的采样点不至于过度稀疏,为了弥补在无纹理下立体匹配失效的情况,同时保留原本LSS中的深度估计模块,将其立体匹配估计出的深度进行融合得到最后更准确地深度表达。不过存在需要知道准确帧间 [ R ∣ t ] [R|t] [R∣t]的问题,在实际工程化中是较难实现的。
对于从相机中恢复深度信息,其来源可以划分为如下几种情况:
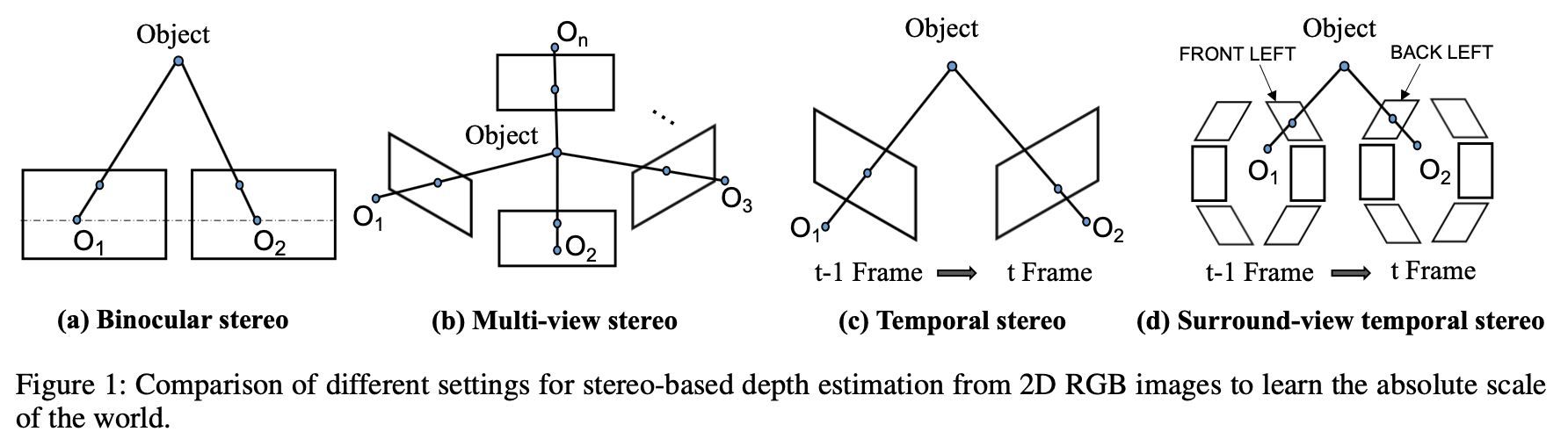
- a)给定基线下的双目立体匹配。
- b)给定多个相机位姿关系的MVS算法。
- c)使用单个相机从运动中恢复深度,但是需要给出帧与帧之间的位姿变换关系。
- d)自动驾驶场景下将周视相机作为一个整体,使用类似运动中恢复深度的策略得到各个相机下的深度信息。
2. 方法设计
2.1 整体pipeline
由文章方法构建的BEV检测算法pipeline见下图所示:
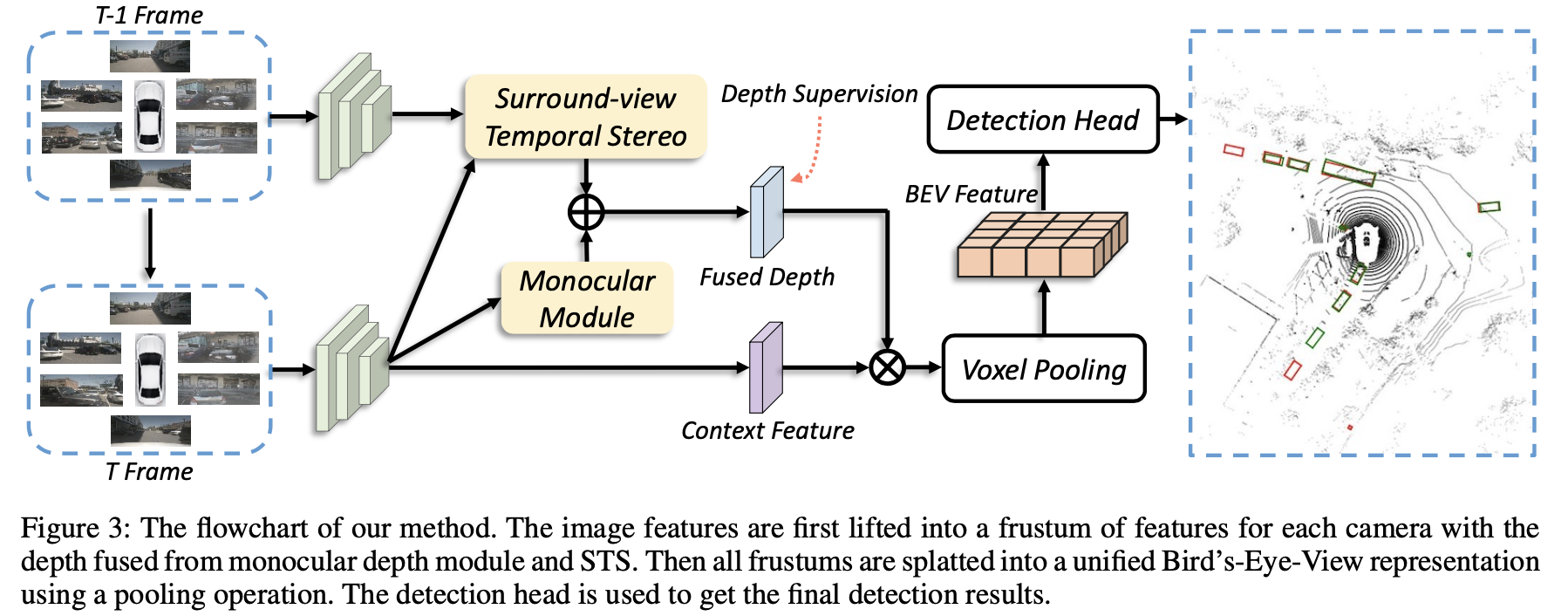
从文中可以看到相比原本的LSS算法,其增加了使用之前帧构建立体匹配(STS,Surround-view Temporal Stereo)去估计深度信息,之后再与原本的深度估计模块结果进行融合。
2.2 STS构建
STS部分的处理流程见下图所示:
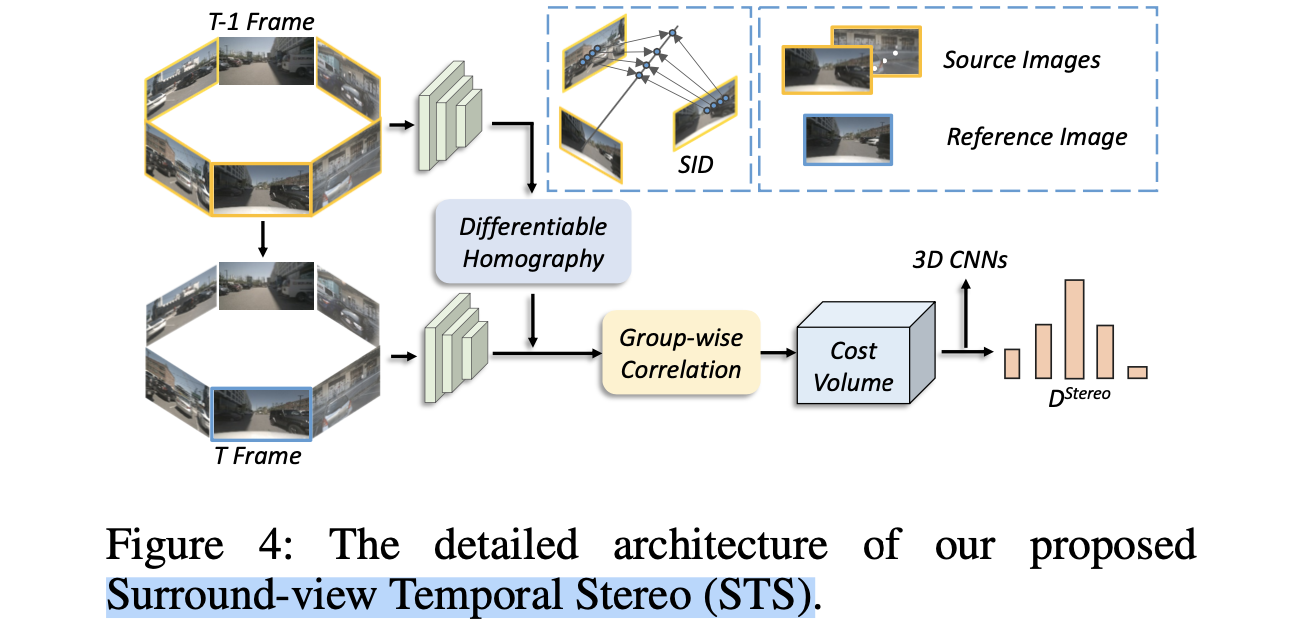
输入的周视图像会被backbone处理抽取图像特征
F
i
∈
R
C
F
∗
H
n
∗
W
n
F_i\in R^{C_F*\frac{H}{n}*\frac{W}{n}}
Fi∈RCF∗nH∗nW,那么使用当前帧(reference) 和 之前帧(source) 的特征就可以在给定的深度划分(
D
D
D) 上计算匹配特征了。但是在这之前需要完成当前帧到之前帧的warp操作(这里会计算source中),这里使用source中
j
j
j个相机到reference中第
i
i
i个相机的转换,记为
H
i
j
H_{ij}
Hij
H
i
j
(
d
)
=
K
j
⋅
R
j
⋅
(
I
−
(
T
i
−
T
j
)
⋅
n
1
T
d
)
⋅
R
i
T
⋅
K
i
−
1
H_{ij}(d)=K_j\cdot R_j\cdot (I-\frac{(T_i-T_j)\cdot n_{1}^T}{d})\cdot R_i^T\cdot K_i^{-1}
Hij(d)=Kj⋅Rj⋅(I−d(Ti−Tj)⋅n1T)⋅RiT⋅Ki−1
则,reference中的特征到source下的特征转换被描述为:
P
i
j
s
o
u
r
c
e
=
H
i
j
⋅
P
i
r
e
f
,
j
=
1
,
…
,
N
P_{ij}^{source}=H_{ij}\cdot P_i^{ref},\ j=1,\dots,N
Pijsource=Hij⋅Piref, j=1,…,N
完成reference到source的投影之后,对于source中的第
i
i
i个相机,只会考虑有效的投影点
P
i
j
s
o
u
r
c
e
^
P_{ij}^{\hat{source}}
Pijsource^,这些投影点组成warp之后的特征
V
i
∈
R
C
F
∗
D
′
∗
H
n
∗
W
n
V_i\in R^{C_F*D^{'}*\frac{H}{n}*\frac{W}{n}}
Vi∈RCF∗D′∗nH∗nW。之后再与source中的特征进行分组计算cost volume:
S
i
g
=
1
C
F
/
G
⟨
F
i
⋅
V
i
⟩
S_i^g=\frac{1}{C_F/G}\langle F_i\cdot V_i\rangle
Sig=CF/G1⟨Fi⋅Vi⟩
其中
⟨
⋅
⟩
\langle \cdot \rangle
⟨⋅⟩代表矩阵内积,之后这些特征就会经过几层3D卷积之后被用于去计算stereo matching下的深度预测结果了。
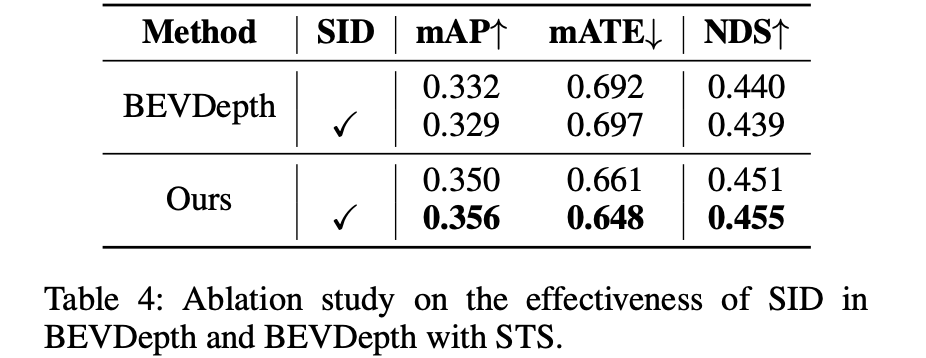
在上面构建cost volume的时候是按照给定的深度进行划分的,通常采用的是深度方向上均匀划分的方案,但是这种方案由于相机的投影过程会导致近处变得稀疏,如下图中中间的效果所示:

对此,文章采用SID的方法进行投影,在给定最大最小深度值和需要划分的深度bins下其划分准则被描述为:
d
k
=
e
x
p
(
l
o
g
(
D
m
i
n
)
+
l
o
g
(
D
m
a
x
D
m
i
n
)
∗
k
C
D
)
,
k
=
1
,
…
,
D
d_k=exp(log(D_{min})+\frac{log(\frac{D_{max}}{D_{min}})*k}{C_D}), k=1,\dots,D
dk=exp(log(Dmin)+CDlog(DminDmax)∗k),k=1,…,D
这里的采样方法对性能带来的影响:
STS部分输出第
i
i
i个相机深度估计结果被描述为
D
i
s
t
e
r
e
o
D_i^{stereo}
Distereo。
2.3 深度结果融合
在STS中输出
D
i
s
t
e
r
e
o
D_i^{stereo}
Distereo,将其与LSS中原本的深度估计结果
D
i
m
o
n
o
D_i^{mono}
Dimono进行融合,其融合策略为:
D
i
p
r
e
d
=
σ
(
D
i
s
t
e
r
e
o
+
D
i
m
o
n
o
)
D_i^{pred}=\sigma(D_i^{stereo}+D_i^{mono})
Dipred=σ(Distereo+Dimono)
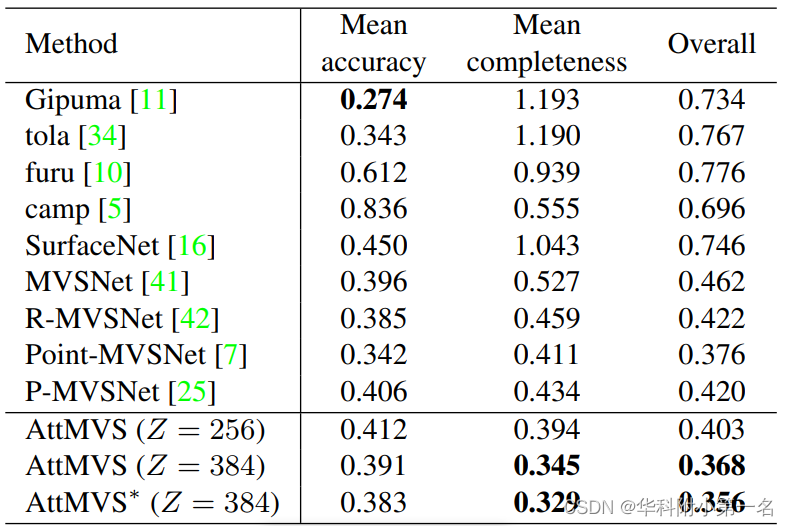
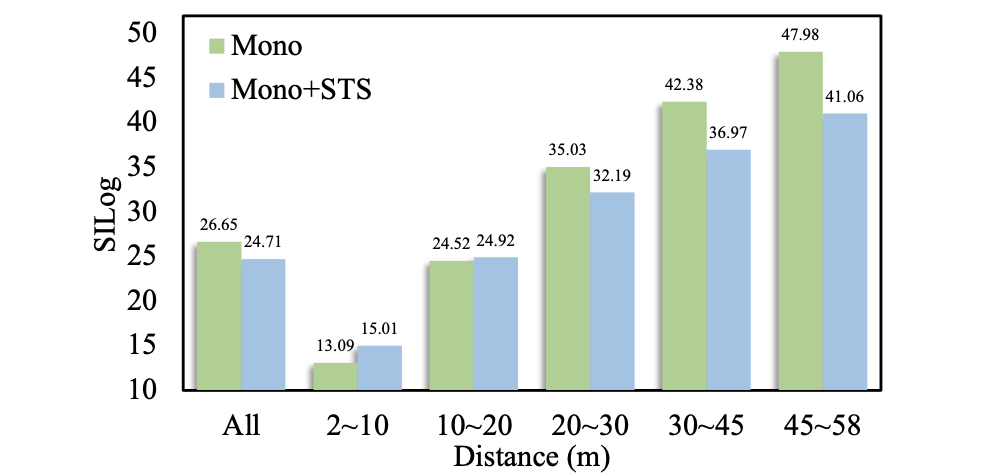
深度估计结果融合之后的深度估计性能表现:
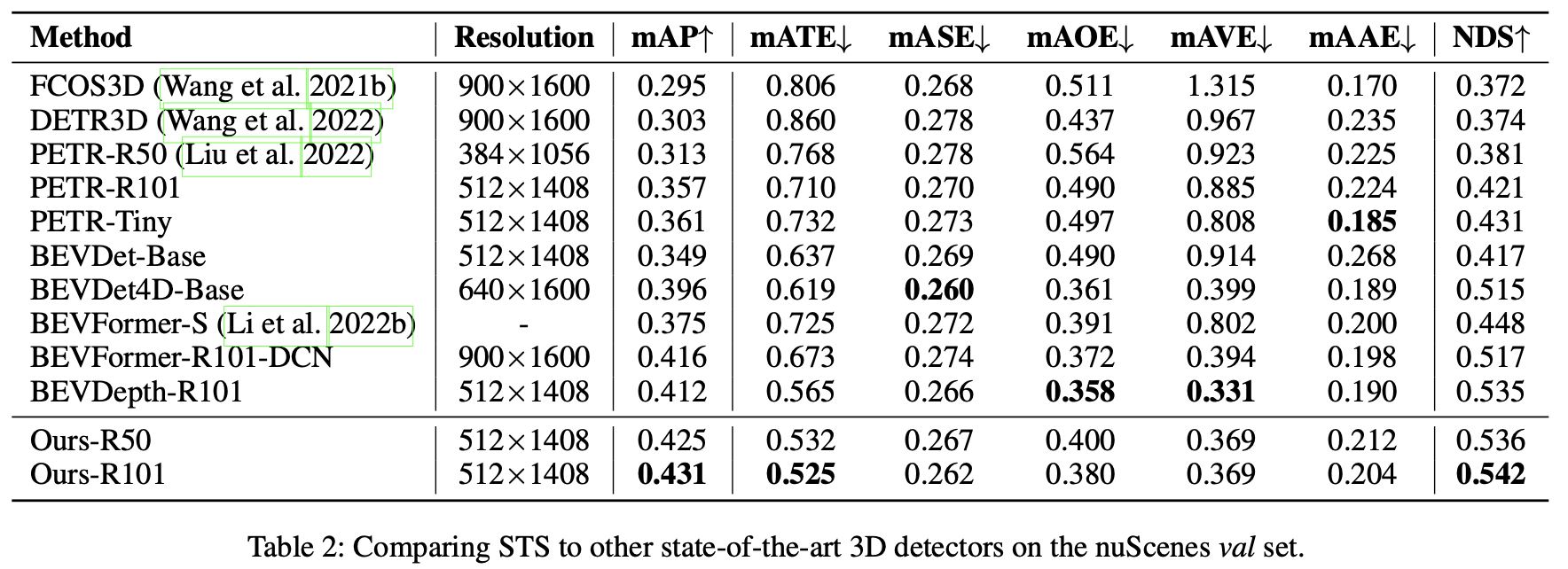
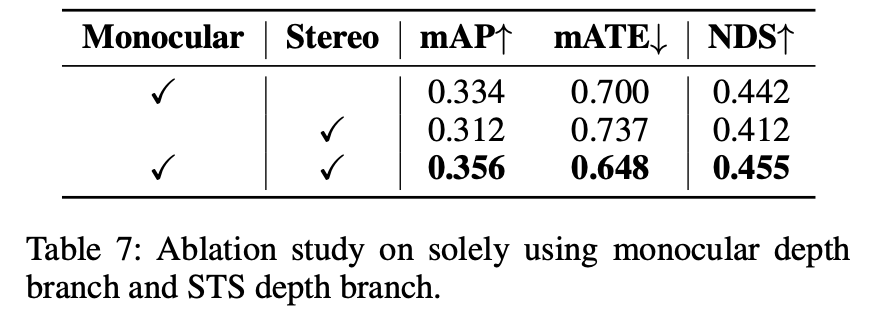
对于检测性能的影响:
3. 实验结果