支持向量机
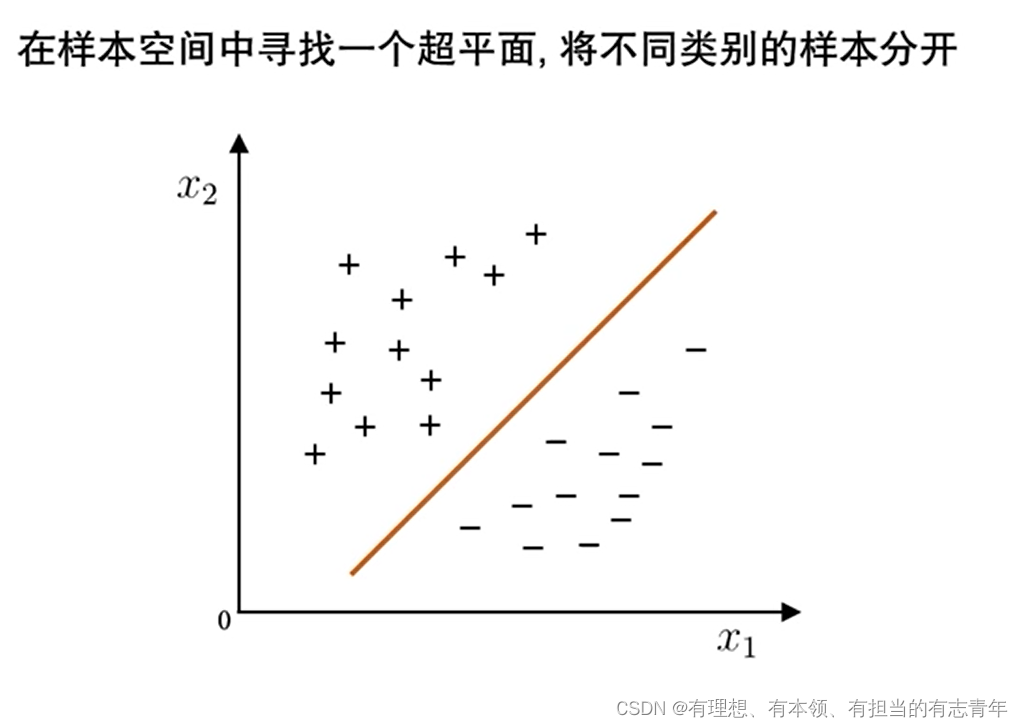
任务:找到超平面
在样本空间中,找到最好的超平面把样本分开,即找到正中间的超平面
满足
- 该超平面 分开了两类
- 该超平面 最大化支持向量间隔
- 该超平面处于 间隔中间,到所有支持向量距离相等
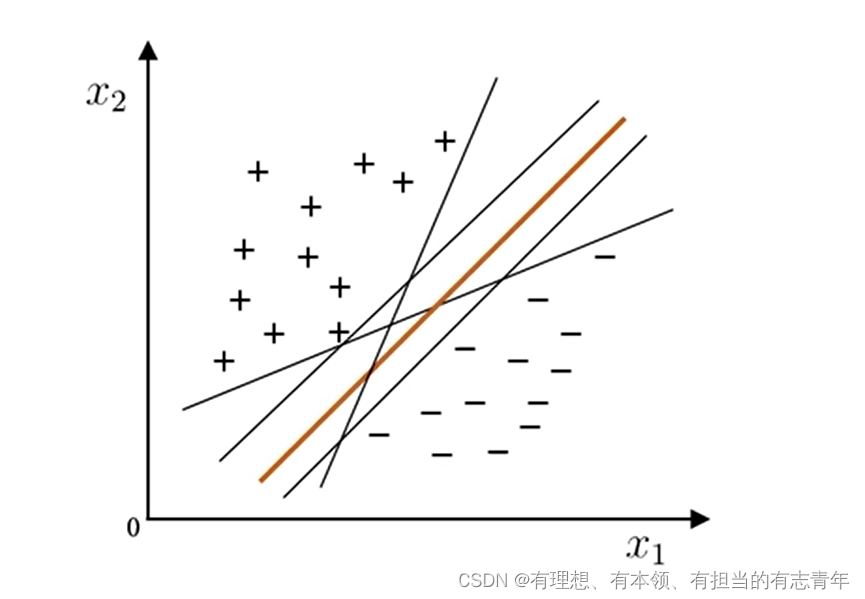
如何找:表示出间隔求最大化
以二分类为例,决定超平面的样本是离超平面最近的两类样本,称为支持向量。支持向量至少有两个,可能有多个。两类支持向量见的距离称为间隔
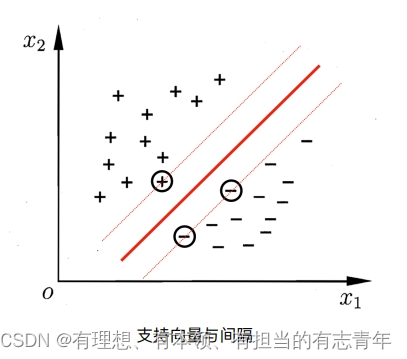
为了方便起见,我们让过两类的支持向量的超平面,称为正负面。我们可以通过代数变换,把正负面的方程变换为
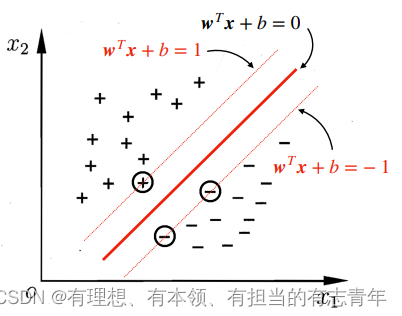
为什么能这么变换?因为支持向量到最中间超平面(我们想要的)的距离相等
经过上面的变换,我们就能把间隔表示为
γ = 2/ ||w||
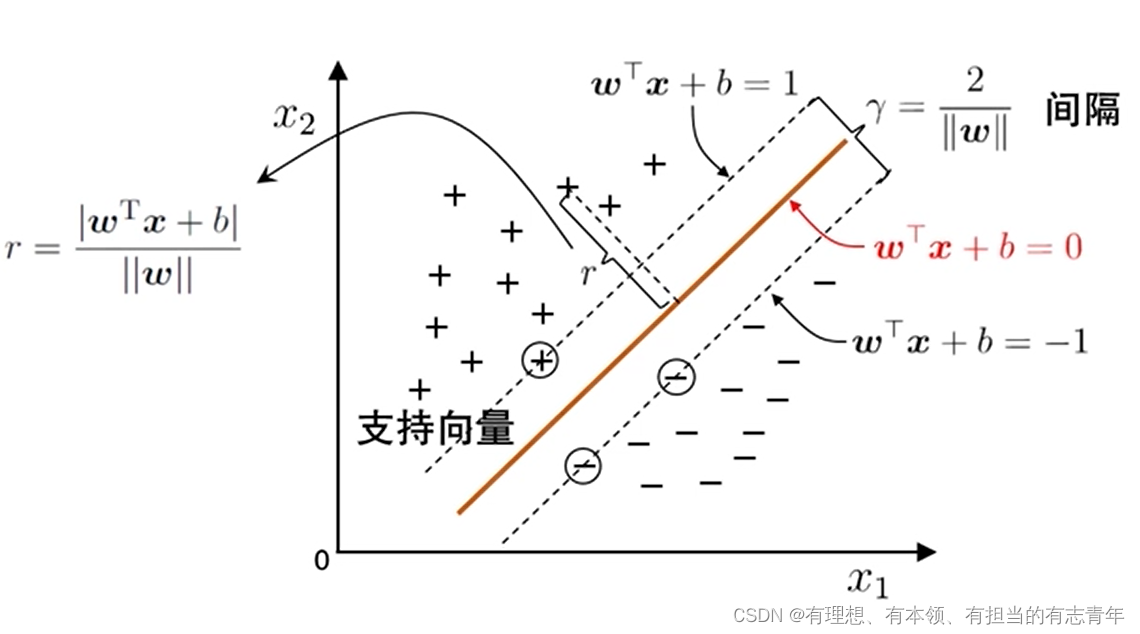
转化为求γ最大即可

拉格朗日乘子法


SMO求解方法

数据混在一块儿分不出来怎么办
将样本从原始空间映射到更高维的特征空间,使得样本线性可分
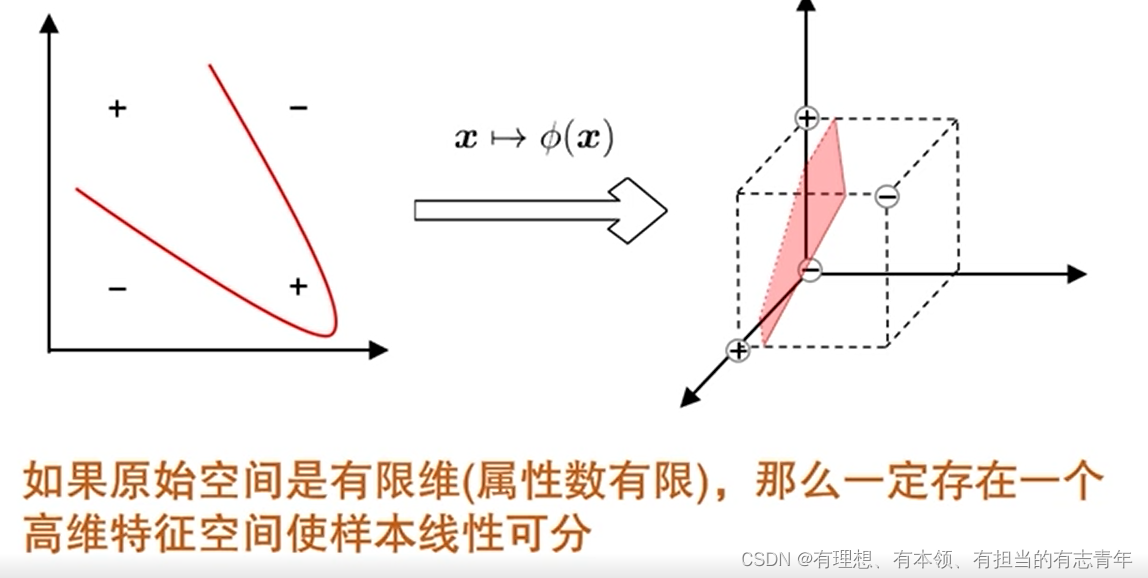
转化后

总是以内积形式出现,单独算不好处理,考虑设计核函数

如何找核函数
我们不能找到一个唯一的最优函数来替代φφT,只能从核函数集合中选择一个

缓解过拟合:软间隔
引入软间隔,允许在一些样本上不满足约束
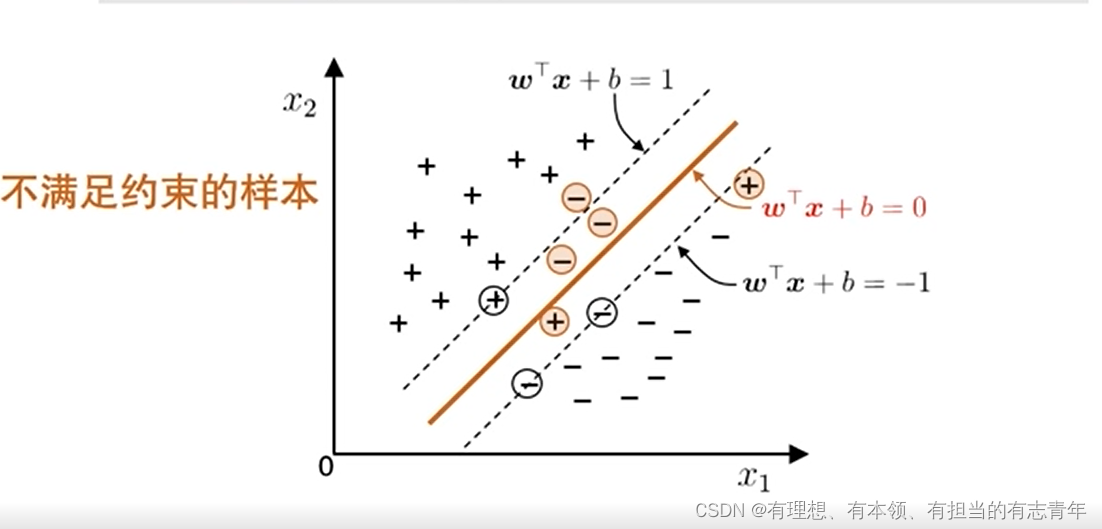

由于0/1函数不易优化,我们选择一个替代函数
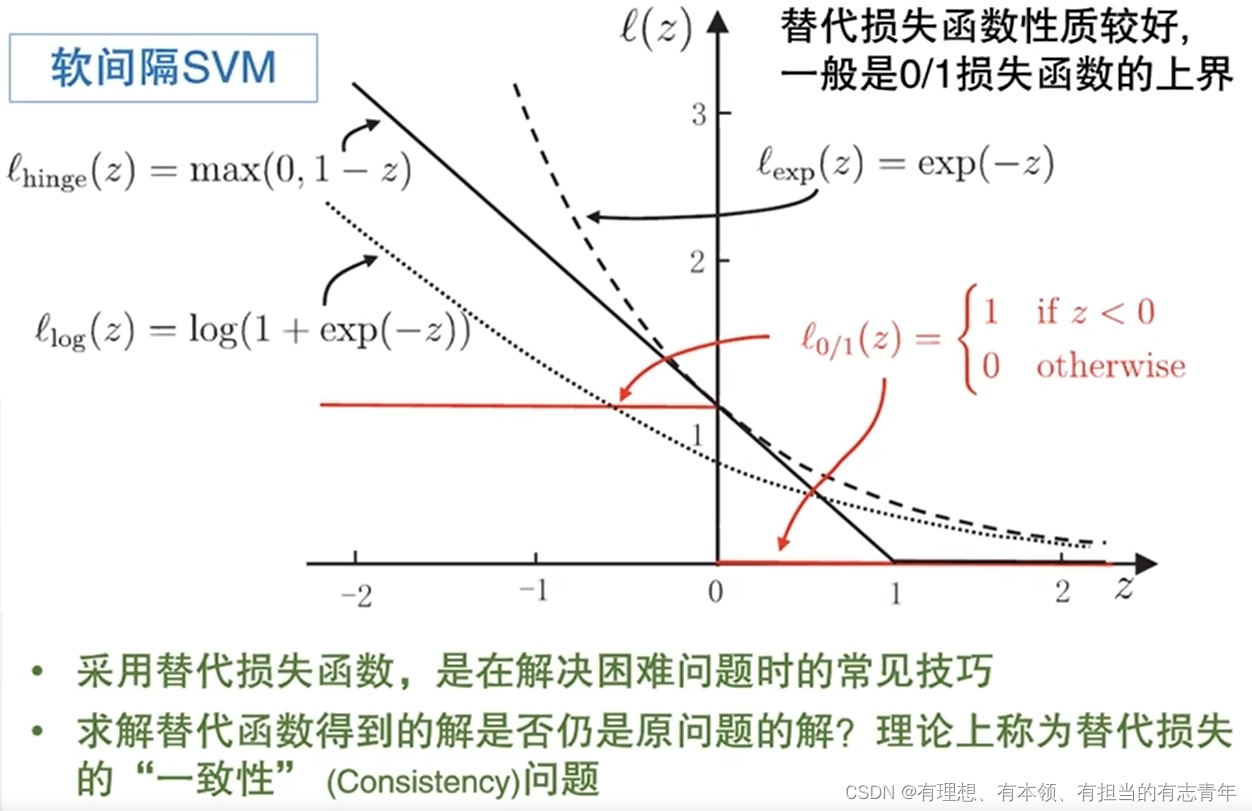
引入拉格朗日乘子法求解

应用