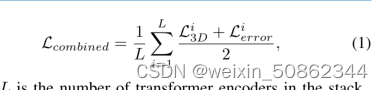连载文章,长期更新,欢迎关注:
Gmapping代码实现相对简洁,非常适合初学者入门学习。但是Gmapping属于基于滤波方法的SLAM系统,明显的缺点是无法构建大规模的地图,这一点已经在第7章中讨论过了。而基于优化的方法则可以构建大规模的地图,基于优化的方法实现的激光SLAM算法也有很多,比如Hector、Karto、Cartographer等。而Cartographer是其中获好评最多的算法,Cartographer是这几种算法中提出时间最新、开发团队来自著名的谷歌公司、代码的工程稳定性较高、少有的建图和重定位兼具的算法。所以,下面将从原理分析、源码解读和安装与运行这3个方面展开讲解Cartographer算法。
8.2.1 Cartographer原理分析
其实基于优化方法的激光SLAM已经不是一个新研究领域了,谷歌的Cartographer算法主要是在提高建图精度和提高后端优化效率方面做了创新。当然Cartographer算法在工程应用上的创新也很有价值,Cartographer算法最初是为谷歌的背包设计的建图算法,谷歌的背包是一个搭载了水平单线激光雷达、垂直单线激光雷达和IMU的装置,用户只要背上背包行走就能将环境地图扫描出来。由于背包是背在人身上的,最开始Cartographer算法是只支持激光雷达和IMU建图的,后来为了适应移动机器人的需求,将轮式里程计、GPS、环境已知信标也加入到算法,也就是说Cartographer算法是一个支持多激光雷达、IMU、轮式里程计、GPS、环境已知信标的传感器融合建图算法。下面将结合Cartographer算法的核心论文[3]对Cartographer的原理展开分析。
基于优化方法的SLAM系统通常采用前端局部建图、闭环检测和后端全局优化这种经典框架,如图8-8所示。
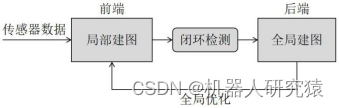
图8-8 基于优化的SLAM经典框架
1.局部建图
局部建图就是利用传感器扫描数据构建局部地图的过程,在第7章中已经介绍过,机器人位姿点、观测数据和地图之间通过约束量建立联系。如果在机器人位姿准确的情况下,可以把观测到的路标直接添加进地图。由于从机器人运动预测模型得到的机器人位姿存在误差,所以需要先用观测数据对这个预测位姿做进一步更新,以更新后的机器人位姿为基准来将对应的观测加入地图。用观测数据对这个预测位姿做进一步更新,主要有下面几种方法:
- Scan-to-scan matching
- Scan-to-map matching
- Pixel-accurate scan matching
最简单的更新方法,就是Scan-to-scan matching方法。由于机器人相邻两个位姿对应的雷达扫描轮廓存在较大的关联性,在预测位姿附近范围内将当前帧雷达数据与前一帧雷达数据进行匹配,以匹配位姿为机器人位姿的更新量。但是,单帧雷达数据包含的信息太少了,直接拿相邻两帧帧雷达数据做匹配更新会引入较大误差,并且雷达数据更新很快,这将导致机器人位姿的误差快速累积。
而Scan-to-map matching方法则不同,其采用当前帧雷达数据与已构建出的地图做匹配。由于已构建出的地图信息量相对丰富稳定,所以并不会导致机器人位姿的误差累积过快的问题,如图8-9所示。Cartographer的局部建图就是采用这种方法,也称为局部优化。
而Pixel-accurate scan matching方法,其匹配窗口内的搜索粒度更精细,这样能得到精度更高的位姿,缺点是计算代价太大,后面将讲到的Cartographer闭环检测采用的就是这种方法。当然,关于闭环检测也有很多别的方法,比如extracted features matching方法、histogram-based matching方法、machine learning方法等,感兴趣的读者可以查阅相关资料。
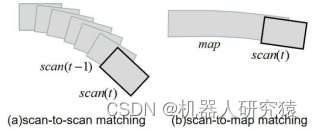
图8-9 scan-to-scan与scan-to-map对比
在介绍Cartographer局部建图的具体过程之前,需要先了解一下Cartographer地图的组成形式。Cartographer采用局部子图(submap)来组织整个地图,其中若干个激光雷达扫描帧(scan)构成一个submap,然后所有的submap构成全局地图(submaps),如图8-10所示。
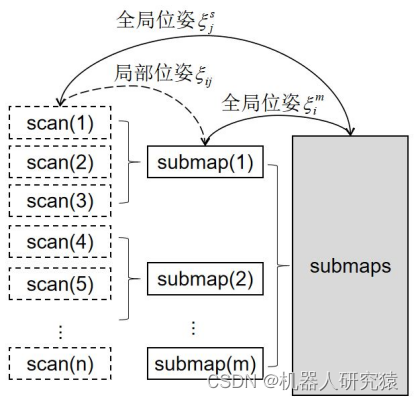
图8-10 Cartographer地图结构
不管是雷达扫描帧(scan),局部子图(submap),还是全局地图(submaps),它们之间都是通过位姿关系进行关联的。这里只讨论2D SLAM建图,所以位姿坐标可以表示为。假设机器人初始位姿为
,该位姿处雷达扫描帧为scan(1),并利用scan(1)初始化第一个局部子图submap(1)。利用Scan-to-map matching方法计算scan(2)相应的机器人位姿
,并基于位姿
将scan(2)加入submap(1)。不断执行Scan-to-map matching方法添加新得到的雷达帧,直到新出现的雷达帧完全包含在submap(1)中时,换句话说就是新雷达帧观测不到submap(1)之外的新信息时,就结束submap(1)的创建。这里假设submap(1)由scan(1)、scan(2)和scan(3)构建而成,然后重复上面的步骤构建新的局部子图submap(2)。而所有局部子图{submap(m)}就构成了最终的全局地图submaps。
可以发现,每个雷达扫描帧都对应一个全局地图坐标系下的全局坐标,同时该雷达扫描帧也被包含在对应的局部子图中,也就是说该雷达扫描帧也对应一个局部子图坐标系下的局部坐标。而每个局部子图以第一个插入的雷达扫描帧为起始,该起始雷达扫描帧的全局坐标也就是该局部子图的全局坐标。这样的话,所有雷达扫描帧对应的机器人全局位姿和所有局部子图对应的全局位姿
通过Scan-to-map matching产生的局部位姿
进行关联,这些约束实际上就构成了位姿图。当检测到闭环时,对整个位姿图中的所有位姿量进行全局优化,那么
和
中的所有位姿量都会得到修正,每个位姿上对应的地图点也相应的得到修正,这就是全局建图。接下来详细介绍一下利用Scan-to-map matching方法构建局部子图的过程。
局部子图构建过程涉及到很多坐标系变换的内容,这里就来详细讨论。首先雷达扫描一圈得到的距离点是基于雷达旋转中心为坐标系的取值。那么在一个局部子图中,以第一帧雷达位姿为参考,后加入的雷达帧位姿用相对转移矩阵
表示。这样的话,雷达帧中的数据点
就可以用式(8-10)所示的公式转换成局部子图坐标系中表示。
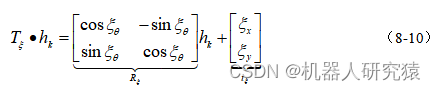
与Gmapping类似,Cartographer中的子图(submap)也采用概率栅格地图(Probability Grids)。所谓概率栅格地图,就是连续2D空间被换分成一个个离散的栅格,栅格的边长r为分辨率,通常栅格地图的分辨率r=5cm。那么扫描到的障碍点就替换成用该障碍点所占据的栅格表示。用概率来描述栅格中是否有障碍物,概率值越大说明存在障碍物的可能性越高。
接下来就可以讨论新雷达数据被加入到子图(submap)的过程了,先按式(8-10)将新雷达数据转换到子图坐标系,这时候新雷达数据点会覆盖子图的一些栅格,每个栅格存在3种状态,即未知(unknown)、非占据(miss)和占据(hit)。如图8-11所示,雷达扫描点所覆盖的栅格就应该为占据(hit)状态;而雷达扫描光束起点与终点区域内肯定就没有障碍物,该区域覆盖的栅格就应该为非占据(miss)状态;由于雷达扫描分辨率和量程限制,未被雷达扫描点所覆盖的栅格就应该为未知(unknown)状态。由于子图(submap)中的栅格可能不只被一帧雷达扫描点所覆盖,所以需要对栅格的状态进行迭代更新,具体分下面2种情况处理。
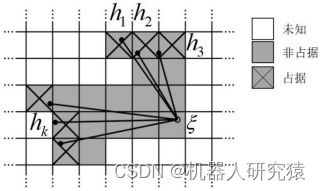
图8-11 雷达数据点栅格化
情况1,在当前帧新雷达数据点覆盖的栅格中,如果该栅格之前从未被雷达数据点覆盖,即未知状态,那么直接用式(8-11)执行初始更新。其中,栅格
若是被新雷达数据点标记为占据(hit)状态,那么就用占据概率
给该栅格赋予初值;同理栅格
若是被新雷达数据点标记为非占据(miss)状态,那么就用非占据概率
给该栅格赋予初值。概率
和
的取值有雷达概率观测模型给出,见第7章相关内容。
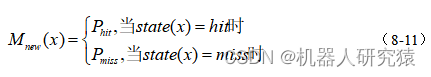
情况2,在当前帧新雷达数据点覆盖的栅格中,如果该栅格之前已经被雷达数据点覆盖过,也就是栅格已经有取值
,那么就用式(8-12)执行迭代更新。其中,栅格
若是被新雷达数据点标记为占据(hit)状态,那么就用占据概率
对
进行更新;同理栅格
若是被新雷达数据点标记为非占据(miss)状态,那么就用非占据概率
对
进行更新。式中odds是一个反比例函数,
是
的反函数。而clamp是一个区间限定函数,当函数值超过设定区间的最大值时都取最大值处理,当函数值超过设定区间的最小值时都取最小值处理。
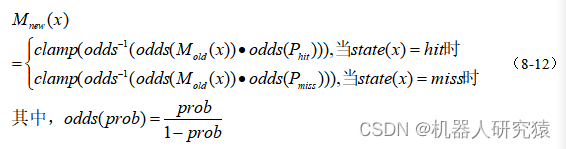
Cartographer所采用的这种栅格更新机制,能有效降低环境中动态障碍物的干扰。比如建图过程中出现了一个行走的人,那么行走的人经雷达扫描后出现在局部子图栅格的位置每次都不同。假如前一时刻栅格上出现人,
被占据概率
赋予了初值;而下一时刻,由于人的位置移动了,
此时将被标记成非占据(miss)状态,由式(8-11)所示更新方法可知,用非占据概率
对
进行更新后,栅格
的概率取值变小了。随着越来越多次更新,栅格
的概率将接近0,也就是说动态障碍物被清除掉了。
以上所讨论的新雷达数据加入到子图(submap)的操作,基于雷达位姿误差较小的条件。由于从机器人运动预测模型得到的机器人位姿存在较大误差,所以需要先用观测数据对这个预测位姿做进一步更新,以更新后的机器人位姿为基准来将对应的观测加入地图。Cartographer中采用了所谓的Scan-to-scan matching方法,对雷达位姿
做局部优化,下面讨论具体过程。
在将新雷达数据加入到子图(submap)之前,先在运动预测出的雷达位姿附近窗口内做搜索匹配,如式(8-13)所示。其实这就是一个非线性最小二乘问题,Cartographer采用了自家的Ceres非线性优化工具来求解该问题,关于Ceres的内容已经在第7章介绍过了。而式中的约束量由函数构建,
是一个双立方插值(bicubic interpolation),也叫平滑。
其实就是用来确定雷达扫描轮廓
与局部子图(submap)之间的匹配度,匹配度取值范围为[0,1]区间。
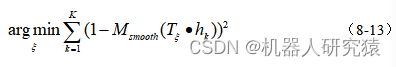
2.闭环检测
上面介绍的局部建图过程,采用了式(8-12)对位姿进行了局部优化,有效降低了局部建图中的累积误差。但是随着建图规模的扩大,比如上千平米的地图时,总的累积误差还是会很大,也就是在地图构建得很大时,地图出现重影的现象,如图8-12所示。
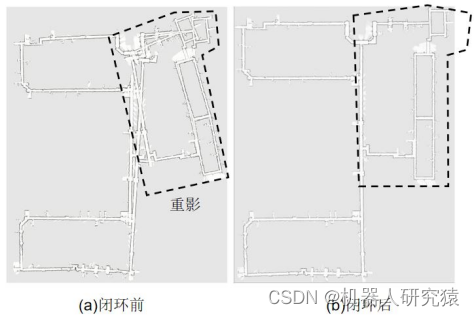
图8-12 地图重影
其实就是机器人在运动了很远的距离又回到了之前走过的地方,由于局部建图位姿累积误差的存在,使得当前机器人位姿与之前走过的同一个地方并不重合,也就是说真实情况里,这两个地方应该是同一个。自然这两个机器人位姿对应的局部地图也就不重合了,就出现了所谓的重影。借助闭环检测技术,可以检测到机器人位姿闭环这一情况,将闭环约束加入整个建图约束中,并对全局位姿约束进行一次全局优化,这样就能得出全局建图结果。下面将主要对闭环检测过程过程进行讲解。
在局部建图过程中,使用了Scan-to-scan matching方法进行位姿局部优化。而闭环检测中,搜索匹配的窗口
更大,位姿
计算精度要求更高,所以需要采用计算效率更高精度更高的搜索匹配算法。首先来看一下回环检测问题的数学表达,如式(8-14)所示。式中的
函数值其实就是雷达数据点
覆盖的栅格所对应概率取值,当搜索结果
就是当前帧雷达位姿真实位姿时,当前帧雷达轮廓与地图匹配度很高,即每个
函数值都较大,那么整个求和结果也就最大。
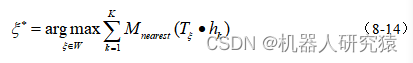
针对式(8-14)所示求最值的问题,最简单的方法就是在窗口内暴力搜索。假设所选窗口
大小为
,搜索步长为
,同时方向角搜索范围假设为30°,搜索步长为
,那么总的搜索步数为
步。每步搜索都要计算式(8-14)所示的匹配得分,如式(8-15)所示。

可以发现,每步搜索都要计算 维数据的求和运算,而整个搜索过程的计算量为
。虽然暴力搜索匹配可以避免陷入局部最值的问题,但是计算量太大根本没法在机器人中做到实时计算。这种暴力搜索,就是所谓的Pixel-accurate scan matching方法。
采用暴力搜索来做闭环检测显然行不通,因此谷歌在Cartographer中采用分支定界(branch-and-bound)方法来提高闭环检测过程的搜索匹配效率。分支定界简单点理解,就是先以低分辨率的地图来做匹配,然后逐步提高分辨率,如图8-13所示。假设地图原始分辨率为r=1cm,将其进行平滑模糊处理得到分辨率为r=2cm的地图,继续平滑模糊处理可以得到分辨率为r=4cm和r=8cm的地图。

图8-13 地图分辨率
现在来考虑在不同分辨率地图,其搜索窗口的策略。为了讨论方便,这里举一个简单例子,假设所选取的窗口
。先以r=8cm分辨率最低的地图开始搜索,这时候窗口
可以按照分辨率被化分成4个区域,也就是4个可能的解,用式(8-15)计算每个区域的匹配得分。选出得分最高的那个区域,将该区域作为新的搜索窗口,并在r=4cm分辨率的地图上开始搜索,同样将窗口按照分辨率化分成4个区域,用式(8-15)计算每个区域的匹配得分。不断重复上面的细分搜索过程,直到搜索分辨率达到最高分辨率为止。整个细分搜索过程,如图8-14所示。
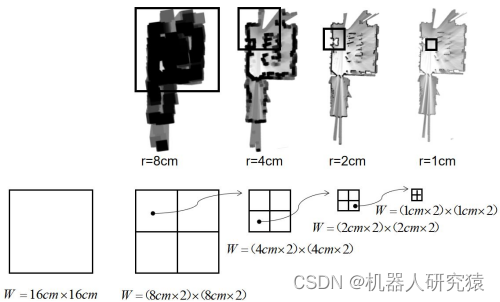
图8-14 细分搜索过程
上面介绍的这种分支定界策略属于广度优先搜索,就是先横向比较同一分辨率下的划分区域的匹配得分,找到得分最高的区域继续划分。而Cartographer中用到的分支定界策略是深度优先搜索,也就纵向比较不同分辨率下划分区域的匹配得分。关于广度优先搜索和深度优先搜索的过程,如图8-15所示。当然在Cartographer分支定界深度优先搜索中,搜索树并不是简单的二叉树,可能每个父节点会分出多个子节点。父节点比子节点代表解空间的分辨率要低,搜索遍历过程会不断进行匹配得分界限判断,并将不符合条件的分支节点进行剪支,大大缩小了搜索空间的维度。通过分支定界法搜索匹配得到的位姿还可以利用前面的Scan-to-map matching方法进一步提高精度,就不多说了。
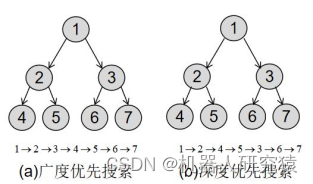
图8-15 广度优先搜索与深度优先搜索
3.全局建图
闭环检测是在程序后台持续运行的,传感器每输入一帧雷达数据,都要对其进行闭环检测。当闭环检测中匹配得分超过设定阈值就判定闭环,此时将闭环约束加入整个建图约束中,并对全局位姿约束进行一次全局优化,这样就能得出全局建图结果,下面详细介绍全局优化过程。
在Cartographer中采用的是稀疏位姿图来做全局优化,稀疏位姿图的约束关系可以从图8-10中构建。所有雷达扫描帧对应的机器人全局位姿和所有局部子图对应的全局位姿
通过Scan-to-map matching产生的局部位姿
进行关联,数学表达如式(8-16)所示。

式中,所有雷达扫描帧对应的机器人全局位姿用集合表示,j是雷达扫描帧的序号;所有局部子图对应的全局位姿用集合
,i是子图的序号。而雷达扫描数据在局部子图中还具有局部位姿,比如
表示序号为j的雷达扫描帧在序号为i的局部子图中的局部位姿,该局部位姿通过Scan-to-map matching方法确定。而损失函数
用于惩罚那些过大的误差项,比如Huber损失函数。可以看出式(8-16)所示的问题其实这就是一个非线性最小二乘问题,Cartographer同样采用了自家的Ceres非线性优化工具来求解该问题。
当检测到闭环时,对整个位姿图中的所有位姿量进行全局优化,那么和
中的所有位姿量都会得到修正,每个位姿上对应的地图点也相应的得到修正,这就是全局建图。
以上分析只是站在Cartographer原理的角度展开讨论的,也就是说Cartographer算法具体源码实现过程的细节可能会与上面的分析有所出入,读者请以源码为准。
8.2.2 Cartographer源码解读
上面讨论完Cartographer的原理,现在就来解读Cartographer的源码,其代码框架如图8-16所示。可以看出Cartographer算法主要由3部分组成,分别为cartographer_ros功能包、cartographer核心库和ceres-solver非线性优化库。本书写作时,最稳定的版本为cartographer_ros-1.0.0+cartographer-1.0.0+ceres-solver-1.13.0,所以下面的分析将以此版本代码展开。
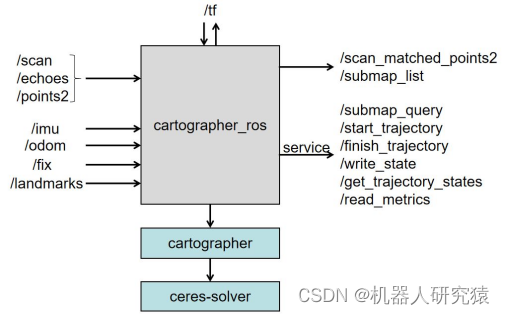
图8-16 Cartographer代码框架
1.cartographer_ros功能包
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
2.cartographer核心库
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
3.ceres-solver非线性优化库
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
8.2.3 Cartographer安装与运行
学习完Cartographer算法的原理及源码之后,大家肯定迫不及待想亲自安装运行一下Cartographer体验一下真实效果。在第1章中已经声明过,本书在Ubuntu18.04和ROS melodic环境下进行讨论。不管是使用X86主机、X86主机虚拟机还是ARM主机,一旦装好Ubuntu18.04系统后,就可以在该系统上安装ROS melodic发行版了。如果你只是想利用数据集离线跑算法,可以选择在X86主机或X86主机虚拟机上运行Ubuntu18.04和ROS melodic,关于这一部分的环境搭建请参考1.2.1节的内容。如果需要在实际机器人上在线跑算法,可以选择在ARM主机上运行Ubuntu18.04和ROS melodic,关于这一部分的环境搭建请参考第5章的内容。所以,下面的讨论假设Ubuntu18.04和ROS melodic环境已经准备妥当了。下面所讨论的Cartographer安装、配置和运行的内容都参考自cartographer_ros官方文档和cartographer官方文档。
1.Cartographer安装
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
2.Cartographer在实际机器人运行
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
参考文献
【1】 张虎,机器人SLAM导航核心技术与实战[M]. 机械工业出版社,2022.