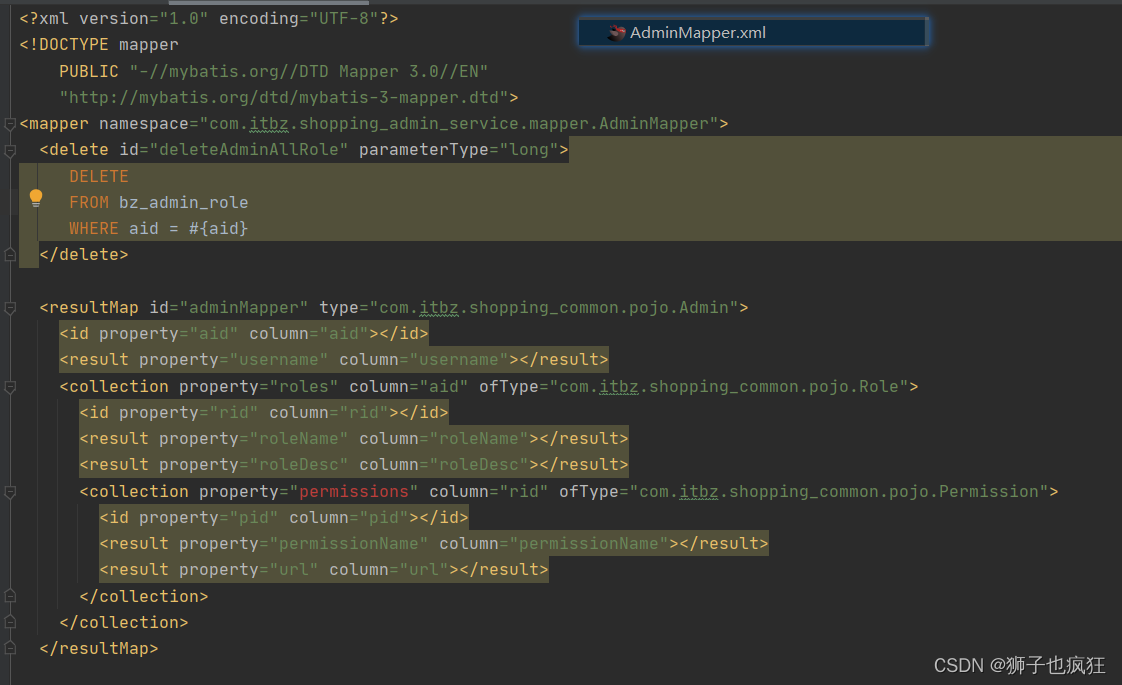
第4章三角学迈向解析化(或分析化)

4.1 三角学迈向解析化的过程简述

4.2 François Vi`eter对三角学解析化的贡献

“Thus the analysis of angular sections involves geometric

and arithmetic secrets which hitherto have been

penetrated by no one(因此，角截面的分析涉及几何和算术的秘密，迄今为止还没有人能破解这些秘密)。”

——François Vi`ete

(说明：“analytic”译为“解析的”，或者“分析的”，以下混用，其意义相同。)

4.1 三角学迈向解析化的过程简述

在伟大的法国数学家弗朗索瓦·维埃特(François Vi`ete，也以他的拉丁文名字 Franciscus Vieta(弗朗索瓦.韦达)著称，1540–1603年)的影响下，三角学开始呈现其现代的分析特征。两个方向的发展使这种进程成为可能：符号代数(symbolic algebra)的兴起——Vi`ete是其中的主要贡献者——以及17世纪上半叶费马(Fermat)和笛卡尔(Descartes)发明的解析几何(analytic geometry)。中世纪数学中繁琐的(cumbersome)文字化代数(verbal algebra)逐渐被简明的符号语句——符号代数(特有符号、拉丁字母、希腊字母、以及其它字母)——所取代，极大地促进了数学著作的写作和阅读。更重要的是，它使数学家能够将代数方法应用到以前以纯几何方式处理的问题。

在Vi`eter的影响下，三角学经历了(underwent)第二个重要变化：它允许无限过程进(infinite process)入它的行列(ranks)。1593年他发现了这个著名的无限积：

$\frac{2}{\pi } = \frac{\sqrt{2}}{2}.\frac{\sqrt{2+\sqrt{2}}}{2}.\frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}. ...$

(Vi`ete使用了缩写词“etc.”代替三个点(...))。这是第一次将一个无限过程明确地写成一个数学公式，而且，它预示着现代解析的开始。[1] (我们将在第11章节证明Vi`eter积。)

在17世纪上半叶，英国有三个人对三角学做出了重大贡献。John Napier(1550–1617) 于1614年发明了对数，极大地促进了数值计算，尤其是三角学。[2] William Oughtred (1574–1660)是第一个尝试系统地使用三角函数符号的人：在他的著作<<Trigonometrie, or, The manner of Calculating the Sides and Angles of Triangles, by the Mathematical Canon, demonstrated>>(由数学经典证明三角学或计算三角形的边和角的方式)(London,1657)，他用简写s, t, se, s co, t co, 和 se co分别代替sine, tangent, secant, cosine (“sine补), cotangent,和 cosecant。[3] (与其冗长的标题相反，除了表格之外，该作品本身仅包含 36 页文字。) 约翰·沃利斯(John Wallis ,1616-1703年)关于无限级数的著作是牛顿在同一领域的发现的直接先驱。沃利斯比他那个时代的任何人都更意识到数学中的综合方法应该让位于分析方法：他是第一个将圆锥曲线视为二次方程而不是几何对象的人，就像希腊人所做的那样。(沃利斯也是第一位撰写数学史的主要数学家，他引入了符号∞来表示无穷大。）他最著名的公式是无穷大乘积

$\frac{\pi }{2}=\frac{2}{1}.\frac{2}{3}.\frac{4}{3}.\frac{4}{5}.\frac{6}{5}.\frac{6}{7}. ... ,$

它与 Vi`ete 的积一起被列为数学中最美丽的公式之一。沃利斯通过大胆的直觉和复杂的插值过程得出了这个结果，这将使现代读者的耐心达到极限；[4] 在第12章中，我们将以更短、更优雅的方式推导出他的这个公式。

解析三角学在17世纪上半叶兴起还有另一个原因：数学在描述我们周围的物理世界方面的作用越来越大。古典三角学的发明者主要对将其应用于天体感兴趣(因此球面三角学最初占主导地位)，而新时代则牢牢扎根于日常生活的机械世界。伽利略发现每个运动都可以沿垂直线分解为两个分量——并且这些分量可以相互独立地处理——一度使三角学在运动研究中不可或缺。 火炮科学——在17世纪它被认为是一门科学——主要关注的是确定大炮发射的炮弹的射程。在不考虑空气阻力的情况下，这距离是R = $\left (v_{0}^{2}sin2\alpha \right )/g$ ，其中 $v_{0}$ 是弹丸(projectile)离开大炮时的速度(velocity)(初速(the muzzle velocity，即炮弹离开炮口的速度)), α表示炮管相对于地面的发射角度，g表示重力加速度(约 $9.81m/s^{2}$ )。这个公式表明，速度已知的情况，距离长短仅取决于角度α ：当α = 45°时，距离达最大，且在另一侧对称地以45°角降落。当然，这些事实早已通过经验为人所知，但它们的理论基础在伽利略时代是全新的。

在 17 和 18 世纪大力研究的另一个力学(mechanics)分支振荡(oscillations)。那个时代的伟大航海需要更精确的导航技术，而这些又取决于更精确的时钟的可用性。这促使科学家们研究各种摆锤和弹簧的振荡。当时一些最伟大的人物都参与了这些研究，其中包括克里斯蒂安·惠更斯(Christiaan Huygens，1629-1695年)和罗伯特·胡克(Robert Hooke，1635-1703年)。惠更斯发现了圆滚摆(cycloidal pendulum)，其摆动周期与振幅无关，而胡克在螺旋弹簧(coiled spring)方面的工作为现代发条手表奠定了基础。 在另一个层面上，制造乐器(从木管乐器和铜管乐器(brass)到键盘乐器和管风琴)的技巧和复杂性的提高促使科学家研究发声体的振动，例如弦(strings)、膜(membranes)、铃(bells)和气管(pipes)。 所有这些都强调了三角学在描述周期性现象中的作用，并导致重点从计算三角学(表格的汇编)转移到三角函数之间的关系——解析三角学的本质。

英国数学家罗杰·科茨(Roger Cotes，1682–1716)在他去世后于1722年出版的著作<<Harmonia mensurarum>>(Harmony of mensuration，调和计算)给出了等价的公式(现代数学符号记法)

Φi = log(cosΦ +i sinΦ)，

其中， $i=\sqrt{-1}$ ，log表示自然对数(基底e=2.718...的对数)。很显然，这公式等同于 Leonhard Euler 的著名公式 $e^{i\Phi }=cos\Phi +isin\Phi$ , 这公式1748年出版于他伟大的著作<< Introductio in analysin infinitorum>>(无穷小量分析简介)中。另见1722年，Abraham De Moivre(1667–1754)推导的公式(尽管以隐式的形式),

$\left ( cos\Phi +isin\Phi \right )^{n}=cos (n\Phi)+isin(n\Phi)$

这是找到实数或复数的n次根的基础。然而，欧拉的权威和他的简介将复数完全纳入三角学：在他的影响下，这个主题变成了真正的解析化。(我们将在第14章回到复数在三角学中的作用。)

这些发展使三角学远离了它最初与三角形的联系。第一个将三角函数定义为粹纯数(pure numbers)而不是三角形中的比率的是德国的Abraham Gotthelf K¨astner (1719–1800)； 1759 年，他写道：“如果 x 表示以度数表示的角度，则表达式 sin x；cos x; tang x等是对应于每个角度的数字。”[5] 今天，当然，我们更进一步，将自变量本身定义为实数而不是角度。

几乎从一开始，微分和积分就被应用于解决力学中的许多问题，首先是离散力学(单个粒子或粒子系统的运动)，然后是连续力学。后者中，十八世纪下半叶的突出问题是振动弦。这个问题从一开始就让数学家们兴奋不已，因为它与音乐有着密切的联系。早在公元前6世纪，毕达哥拉斯就已经发现了一些控制弦振动的定律；这导致他根据数学原理构建了一个音阶。然而，对这个问题的全面研究需要牛顿和莱布尼茨甚至无法使用的方法，即偏微分方程(未知函数及其导数取决于两个或多个自变量的方程)。例如，对于振动的弦(vibrating string)，相关方程是 $\partial ^{2}u/\partial x^{2}=\left ( 1/c^{2} \right )\partial ^{2}/\partial t^{2}$ ,

其中，u = u(x,t)是在时间t处距离弦的一个端点x处的点的平衡位移，c是一个常数，取决于弦的物理参数(其张力和线密度。)

解决这个著名方程(称为一维波动方程)的尝试涉及当时最优秀的数学头脑，其中包括伯努利家族(Bernoulli)、欧拉(Euler)、达朗贝尔(D’Alembert)和拉格朗日(Lagrange)。欧拉和达朗贝尔用代表两个波的任意函数表达了他们的解决方案，一个沿着弦向右移动，另一个向左移动，速度等于常数c。另一方面，丹尼尔·伯努利(Daniel Bernoulli)找到了一个涉及无限系列三角函数的解决方案。由于同一问题的这两种解决方案看起来如此不同，因此出现了是否可以调和它们的问题，如果不能，则找出哪种更通用。法国数学家简·巴蒂斯特·约瑟夫·傅立叶(Jean Baptiste Joseph Fourier,1768–1830) 回答了这个问题。在他最著名的著作<<Th´eorie analytique de la chaleur>>(Analytic theory of heat，热分析理论，1822年)中，Fourier证明了，几乎所有函数，当被视为给定区间内的周期函数时，都可以用以下形式的三角级数表示

$f(x)=a_{0}+a_{1}cos(x)+a_{2}cos(2x)+a_{3}cos(3x)+...+b_{1}sin(x)+b_{2}sin(2x)+b_{3}sin(3x)+...,$

其中，系数和可以通过从函数f(x)计算某些积分而求得。这个傅立叶级数(Fourier series，或称傅立叶序列)在某些方向比我们熟悉的幂级数函数的泰勒展开式(Taylor expansion)更通用；例如，泰勒展开式仅可用于连续且具有连续导数的函数f(x)，而对于傅立叶级数，即使函数f(x)不连续，傅里叶级数也可能存在。我们在第15章将回到这些级数。

傅立叶定理标志着19世纪分析的伟大成就之一。它表明正弦和余弦函数对于研究所有周期现象，无论是简单的还是复杂的，都是必不可少的；事实上，它们是所有此类现象的基石，就像素数是所有整数的基石一样。傅立叶定理后来被推广到非周期函数(在这种情况下无限级数变成积分)，以及涉及非三角函数的级数。这些发展被证明对众多科学分支至关重要，从光学和声学到信息论和量子力学。

注释和资料来源：

1. 最新的发现表明，Hindus在Vi`ete之前可能就已经知道包括π在内的无限序列，参见George Gheverghese Joseph的<<The Crest of the Peacock: Non-European Roots of Mathematics>>(孔雀之冠：数学的非欧洲根源)( Harmondsworth, U.K.: Penguin Books, 1991)，第286-294页。

2. 请参阅我的另一部书<<e: The Story of a Number>>( e: 一个数字的故事)(新泽西州普林斯顿：普林斯顿大学出版社，1994年)。

3. 尽管如此，请参阅第37-38页针对使用这些符号的优秀级部分。另见Florian Cajori, William Oughtred:<<A Great Seventeenth-Century Teacher of Mathematics>>(一位伟大的 17 世纪数学教师)( Chicago: Open Court, 1916)，第35-39页，Cajori指出，Oughtred 书中的表格使用百分制来划分度数(即，分成一百份), 随着手持式计算器的出现，这种做法在我们这个时代重新流行起来。

4. 参见<<A Source Book in Mathematics>>(数学原始资料集) 1200-1800年间版本，D. J. Struik (剑桥, Mass.: 哈佛大学出版社, 1969年),第244-253页。

5. David Eugene Smith, <<History of Mathematics>>(数学史)(1925年初版； New York：Dover出版社会，1958年再版)，卷2, 第163页。K¨astner是第一位完全致力于数学史的数学家(在第4卷中，G¨ottingen，1796–1800)。

4.2 François Vi`eter对三角学解析化的贡献

很遗憾的是，许多帮助将数学塑造成现在形式的人们的名字已经从今天的课程中消失了。其中我们可能会提到Regiomontanus、Napier和Vi`ete，他们都对代数和三角学做出了重大贡献。

弗朗索瓦·维埃特(François Vi`ete)于1540年(具体日期不详)出生于法国西部小镇丰特奈勒孔德(Fontenay le Comte)。他最初从事法律工作，后来参与政治，担任布列塔尼议会议员。正如当时许多学者的做法，他将自己的名字拉丁化为 Franciscus Vieta；但与其他人(其中包括 Regiomontanus)不同，拉丁文版本并未被普遍采用。我们将使用法语 Vi`ete。

在Vi`ete的一生中，他只在闲暇时间练习数学，将其视为一种智力娱乐而不是一种职业。他并不是唯一持这种态度的人：皮埃尔·费马(Pierre Fermat)、布莱斯·帕斯卡(Blaise Pascal)和勒内·笛卡尔(Ren´e Descartes)都在闲暇时对数学做出了巨大贡献，同时正式担任各种政治、外交职务，笛卡尔的情况还包括军事职务。Vi`ete 的科学生涯始于著名军事人物的女儿，即在Phartenay 的Catherine的家庭教师，他为她写了几本教科书。随着他的名声越来越大，他被要求在对西班牙的战争中为君主亨利四世服务。Vi`ete 证明了自己是破解敌人密码的专家：他的联络官给西班牙君主菲利普二世的秘密信息被法国人截获并交给了 Vi`ete，后者成功破译了它。西班牙人对他们的法典被破解感到惊讶，指责法国人使用巫术，“这与基督教信仰的实践背道而驰”。[1]

Vi`ete的最著名的著作是他的<<In artem analyticam isagoge>>(Introduction to the analytical art)(分析艺术导论, Tours, 1591)，被认为是最早的关于符号代数的著作。在这项工作中，他引入了一种接近我们今天使用的符号系统：他用辅音表示已知量，用元音表示未知量。(目前使用 a、b、c 等表示常数，使用 x、y、z 表示未知数的习惯是笛卡尔在 1637 年引入的。) 他将方程定义为“未知量与确定量的比较”和给出了求解方程的基本规则——将一项从方程的一侧移动到另一侧，将方程除以一个公因数，等等。他称他的方法为“ars analytice”和新代数“logistica speciosa”(字面意思是与物种计算相关的艺术，即一般数量)，以区别于旧的“logistica numerosa”。这种从文字化代数(verbal algebra)到符号化代数(symbolic algebra)的转变被认为是数学史上最重要的发展之一。

Vi`ete将代数规则应用于任何数量，无论是算术量还是几何量，从而打破了纯数字与几何实体之间古老的区别。然而，在其他方面，他相当保守。例如，他总是坚持让方程在量纲上(dimensionally)是齐次的(homogeneous)：他会写“M in A aequatur B quadratus”而不是现代方程 mx = b，意思是给定的量M(用辅音表示)乘以未知量(A元音)等于给定数B的平方。这表明他仍然坚持古希腊认为数字之间的运算具有几何性质的观点；由于两个数字的乘积(在几何意义上)表示以这些数字为边的矩形的面积，因此必须将这样的乘积等同于给定边的正方形的面积。(当然，今天，我们将代数量视为纯无量纲数(pure dimensionless numbers)。) 同样有趣的是，Vi`ete 使用现代算术符号“+”和“-”表示加法和减法，但对于相等，他使用文字描述“aequatur。” 对于 $A^{2}$ 他写作“A quadratus”,而对于 $A^{3}$ 他写作“A cubus”(尽管后来他将其简写为“Aq”和“Ac”)。显然，Vi`ete无法完全摆脱旧文字化代数的束缚。他的作品反映了他所处的时代——从旧世界到新世界的过渡时期。

我们特别感兴趣的是Vi`ete对三角学的贡献。他在这个主题上的第一部作品出现在 1571 年，标题为“Canon mathematicus seu ad triangula cum appendicibus”。在这里，他使用所有六个三角函数给出了西方世界第一个系统处理平面和球面三角形的方法。他开发了3个和积公式(例如， $sin\left ( \alpha \right )+sin\left ( \beta \right ) = 2sin\left ( \frac{\alpha +\beta }{2} \right ).cos\left ( \frac{\alpha -\beta }{2} \right )$ ,以及对于sin α+cos β和cos α+cos β对应的类似公式),从这3个公式，Napier可能已经得出了对数的概念，因为它们允许(当反向使用时)将两个数字的乘积减少为另外两个数字的总和。他是第一个以现代形式陈述切线定律的人：(a+b)/(a-b) = tan[(α+β)/2]/tan[(α+β)/2]，其中，a和b是三角形的两条边，α和β分别是这两条边所对向的角(见第152页)。

Vi`ete是第一位将代数知识系统性地应用到三角学中的数学家。例如，令 x = 2 cos α，yn = cos nα ，他获得了这个递推公式

$y_{n} = xy_{n-1} - y_{n-2}$

这个递推公式，当转换回三角函数的时候，就成了

cos nα = 2 cos α . cos(n-1)α - cos(n-2)α

你现在可以使用更小的α倍数的余弦来表示cos(n-1)α和cos(n-2)α ；持续按这个过程进行下去，你可以以只含有cos α和sin α来表示cos nα的公式终结这个过程。Vi`ete 能够对所有n至 10 的整数进行此计算。他为自己的成就感到非常自豪，以至于他惊呼：“因此，角截面的分析涉及几何和算术的秘密，迄今为止还没有人能破解这些秘密。”[2] 为了感激他的壮举，我们提到用cos α和sin α表示 cos nα 和 sin nα的一般公式是Jakob Bernoulli 在1702年发现的，比Vi`ete的工作晚了一百多年。[3]

Vi`ete 擅长将代数变换应用于三角学，这在亨利四世与荷兰驻法国大使的一次著名会面中发挥了重要作用。Adriaen van Roomen(1561-1615年)是鲁汶(比利时)的数学和医学教授，他于1593年发表了一部名为 Ideae mathematicae的著作，其中包含对当时最杰出的在世数学家的调查。[4] 没有任何一个个体的法国数学家，促使荷兰大使轻蔑地谈论法国的科学成就。为了证明他的观点，他向亨利四世提出了一个出现在Ideae中的问题——并向解决它的人颁发了奖金——并吹嘘说法国数学家肯定不会想出一个解决方案。问题是求解 45 次方程

$x^{45}-45x^{43}+945x^{41}-12,300x^{39}+-...+95,634x^{5}-3,795x^{3}+45x=c$

其中，c是常数。

亨利召见维埃特，他立即找到了一个解决方案，并在第二天又想出了22个。所发生的事情在Florian Cajori的<<A History of Mathematics>>中有描述：

Vi`ete已经进行了类似的研究，他立即看到这个令人敬畏的问题只是c = 2sinΦ按照x = 2sin(Φ/45)表达的等式。即，类为45 = 3.3.5，只需将一个角分成五等分一次，然后再分成三等分一次——这样的划分可以是受相应的五次和三次方程的影响。[5]

为了顺应 Vi`ete 的思路，让我们先来看一个更简单的问题。假设我们被要求解方程

$x^{3}-x+1=0$

我们将其重写为

$1=3x-x^3$ ，并且将 2y 代入x：

$\frac{1}{2}=3y-4y^3$ 。

如果我们有敏锐的眼光，我们可能会认识到这个等式和恒等式之间的相似性

$sin\left ( 3\alpha \right )=3sin\left ( \alpha \right )-4sin^{3}\alpha$

事实上，如果我们写成 1/2 = sin 3α 且 y = sinα；则我们可以使得这两个等式重合；以这种新的形式，则问题归结为已知sin 3α = 1/2 ,求sin α。但如果sin 3α = 1/2,则3α = 30°+ 360°k ，其中，k = 0，±1，±2，... ，因此，α = 10°+ 120°k。因此，y = sin(10°+ 120°k)。然而，因为sin函数具有360°周期，因此，仅需考虑值k = 0，1，2就足够。则，我们的3个解为

$x_{0} = 2 sin 10^{\circ}= 0.347....$

$x_{1} = 2 sin 130^{\circ}=1.532....$

以及

$x_{2}=2sin250^{\circ}= -1.879....$

使用计算器我们可以很容易地检查这确实是三个解。因此，三角恒等式帮助我们求解纯代数方程。

现在用三角法求解三次方程是一回事，而求解45次方程则完全是另一回事。那么 Vi`ete 是如何找到他的解的呢？在题为Responsum(1595)的著作中，他概述了他的方法，我们在此用现代符号对其进行总结：令

c = 2 sin 45θ，y = 2 sin 15θ，z = 2 sin 5θ，x = 2 sin 5θ 。

我们的任何是在已知c = 2 sin 45θ的条件下，求得x = 2 sin θ。我们分三步完成。

我们再次从等式 $sin3\alpha =3sin\alpha -4sin^{3}\alpha$ 出发。乘以2 代入α = 15θ , 我们得到

$c=3y-y^{3}$ -----------------------------------(1)

下一步，我们代入α = 5θ，得到

$y=3z-z^{3}$ -----------------------------------(2)

我们现在使用恒等式(identity)

$sin^{5}\alpha =\frac{5}{8}sin\left ( \alpha \right ) -\frac{5}{10}sin\left ( 3\alpha \right ) + \frac{1}{16}sin\left ( 5\alpha \right )$ [6]

乘以32，用θ替换掉α，并且根据x = 2 sin θ来表达2 sin 3θ ，我们得到

$x^{5}=10x-5(3x-x^{3})+z$

化简之后，成为

$z=5x-5x^{3}+x^{5}$ -----------------------------------(3)

如果我们现在将等式(3) 反代入(2)，然后将(2)代入(1 并展开，我们将得到van Roomen 方程！

因此，Vi`ete将原始问题分解为三个更简单的问题。但是为什么他只找到了二十三个解，当我们知道原方程必须有四十五个解时(都是实数，从问题的几何意义如下：将任意角度分成四十五等份)？原因是在Vi`ete时代，人们仍然习惯将角的弦长而不是角的正弦作为基本三角函数(见第2章)；并且由于长度是非负的，他不得不拒绝所有负值的无意义的解。完整的解集由

$x_{k}=2sin\left ( \theta+360^{\circ} k/45\right ) ,k = 0,1,2,... ,44;$

对这些值而言(假设45θ ≤ 180°,不然，sin 45θ 其本身就可能已经是负值了)，只有前面的23个是正值，对应于象限I和II中的角度。

在Vi`ete的诸多其它贡献中，我们应当提到他发现了二次方程 $ax^{2}+bx+c=0$ 的根与其系数之间的关系( $x_{1}+x_{2} = \frac{b}{a},x_{1}.x_{2}=\frac{c}{a}$ )

，尽管他拒绝负根从而使他无法将这种关系表达为通用规则；开发一种近似代数方程解的数值方法；以及发现了以他的名字命名的著名的对于π无穷积(见第50页)。他的大部分著作最初都是为私人发行而印刷的。它们于1646年由荷兰数学家Frans van Schooten(1615-1660年)收集、编辑和出版，即在 Vi`ete 去世四十多年后才正式出版。[7]

在Vi`ete 的最后几年，他卷入了与德国数学家克里斯托弗·克拉维斯(Christopher Clavius，1537-1612年)就教皇格雷戈里十三世于 1582 年下令改革历法的激烈争论。在这件事上是教皇的顾问，使他树敌众多，并导致他的对手拒绝接受他的新代数。同样值得注意的是，Vi`ete一直反对哥白尼体系，而是试图改进托勒密的旧地心体系。我们在这里看到了一个人的内心冲突，(在某些方面)他是一流的创新者，但是，(在另一些方面)他又是一个顽固的保守派。Vi`ete于 1603 年 12 月 13 日在巴黎去世，享年 63 岁。在他的帮助下，代数和三角学开始形成我们今天所知的形式。

注释和资料来源：

1. W. W. Rouse Ball，<< A Short Account of the History of Mathematics>>(数学史简述)(1908年初版；New York:Dover出版社，1906年再版)。

2. Florian Cajori，<<A History of Mathematics>>(数学史)(1893年初版；New York: MacMillan出版社，1919年第二版)。

3. 这些公式是

$cos\left ( n\alpha \right )=cos^{n}\alpha -\frac{n\left ( n-1 \right )}{2n!}.cos^{n-2}\alpha.sin^{2}\alpha + ...$

和

$sin\left ( n\alpha \right )=\frac{n}{1!}cos^{n-1}\alpha .sin\left ( \alpha \right )-\frac{n\left ( n-1 \right )\left ( n-2 \right )}{3!}cos^{n-3}\alpha .sin^{3}\alpha +...+$ 。

4. 在他的著作中，π的值给到小数点后17位，在这一时期是显著的成就。

5. Cajori，<<History of Mathematics>>第138页。

6. 这个恒等式可以通过公式 $sin\left ( 5\alpha \right )=5sin\left ( \alpha \right )-20sin^{3}\alpha +16sin^{5}\alpha$ 将 $sin^{3}\alpha$ 用(3 sin α- sin 3α)/4替换，并求解 $sin^{5}\alpha$ 。

7. van Schooten家族产生了三代数学家，他们都出生并生活在莱顿：上文提到的 Frans senior (1581–1646)、Frans junior和他同父异母的兄弟Petrus(1634–1679)。在这三人中，最著名的是小弗朗斯(Frans junior)，他编辑了笛卡尔的La G'eom'etrie的拉丁文版；他还写了透视(perspective)，提倡使用三维坐标。他是荷兰伟大科学家克里斯蒂安·惠更斯(Christiaan Huygens)的老师。

8.没有英文版的Vi`ete传记。关于他的工作和生活的散记(Sketches)可参见Ball，<<Short Account>>(简记),第229-234页；Cajori, <<History of Mathematics>>第137-139页；Joseph Ehrenfried Hofmann, <<The History of Mathematics>>(数学史),由Frank Gaynor 和 Henrietta O. Midonick翻译自德语(New York：哲学图书馆,1957)，第92-101页;以及DSB(Dictionary of Scientific Biography)中。

内容来源：

<<Trigonometric Delights>> 作者：Eli Maor