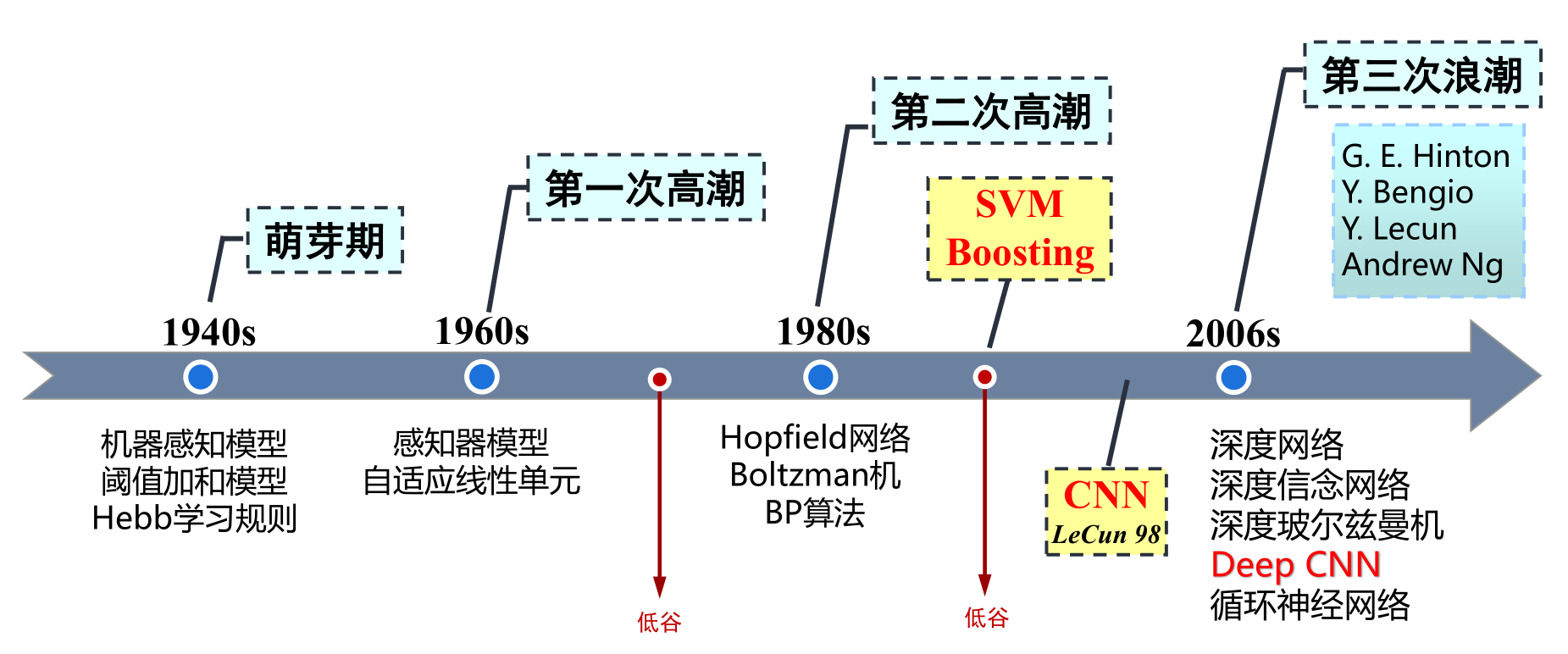
人工神经网络发展浪潮
第三次浪潮——卷积神经网络
加拿大多伦多大学教授,机器学习领域泰斗Geoffery Hinton及其学生在《科学》上发表了一篇论文 (Hinton, G. E . Reducing the Dimensionality of Data with Neural Networks[J]. Science, 2006, 313(5786):504-507.) ,开启了深度学习在学术界和工业界的新浪潮!

卷积计算与卷积神经网络结构
卷积定义
- 卷积是分析数学中的一种重要的运算
- 设 f(x) 和 g(x) 是 R 上的两个可积函数
- 连续形式卷积定义如下
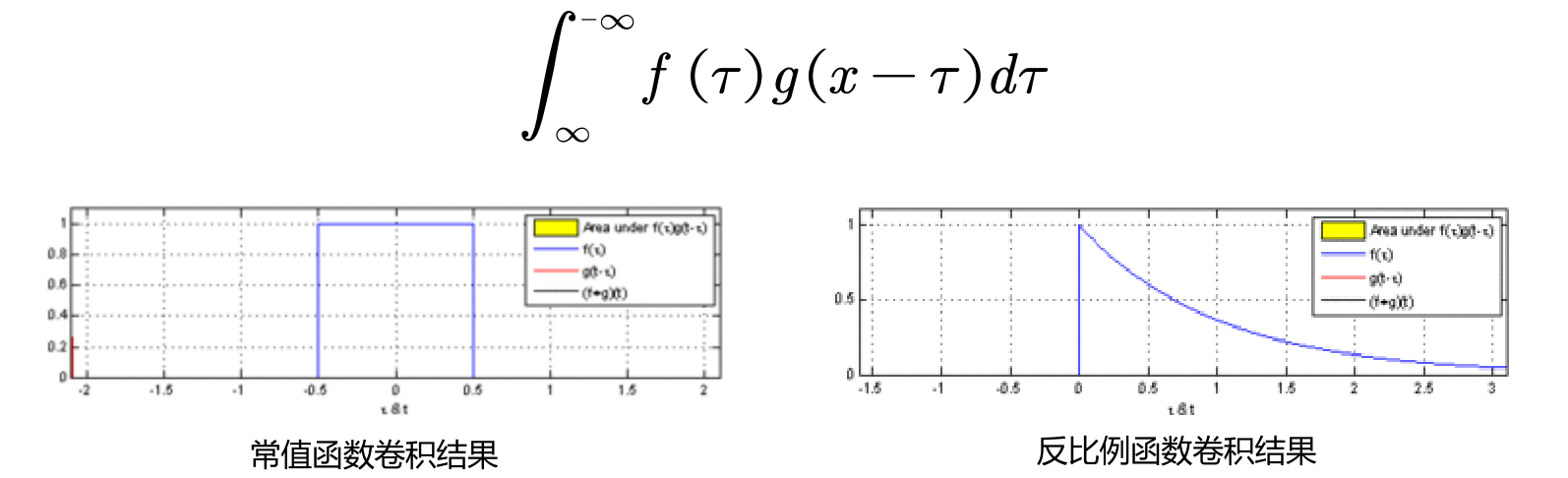
- 离散空间卷积
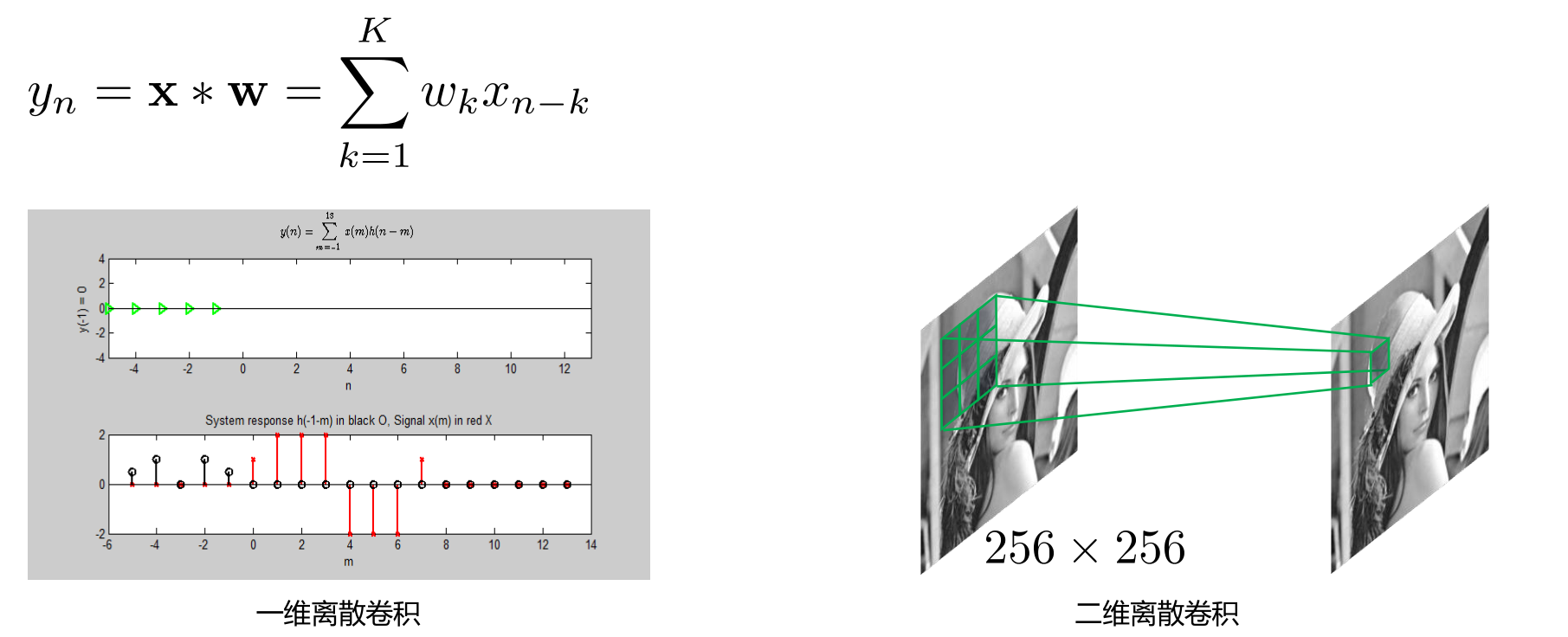
- 连续形式卷积定义如下
卷积中的基本概念
- 卷积核大小 (Kernel Size): 卷积操作感受野,在二维卷积中,通常设置为3,即卷积核大小为3×3
- 步长 (Stride): 卷积核遍历图像时的步幅大小,默认值通常设置为1
- 边界扩充 (Padding): 样本边界的处理方式
- 输入与输出通道 (Channels): 构建卷积层时需定义输入通道数量I,和输出通道数量O,每个网络层的参数量为I×O×K(K为卷积核的参数个数)
更多卷积动图
Convolution animations
N.B.: Blue maps are inputs, and cyan maps are outputs.
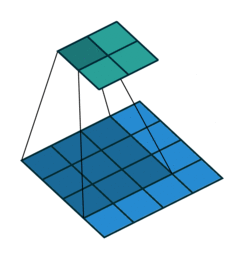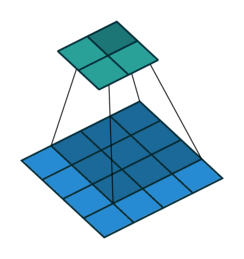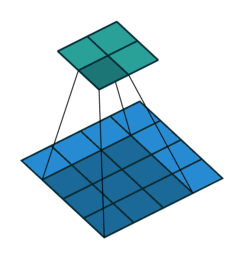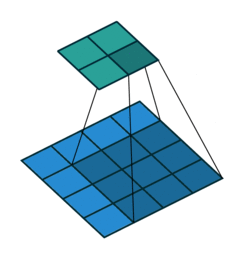 |  | 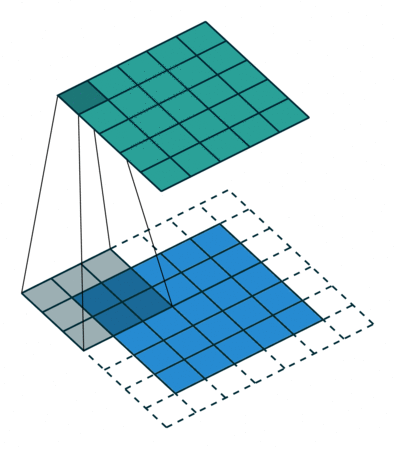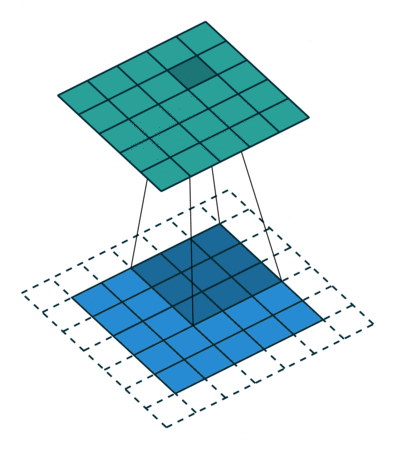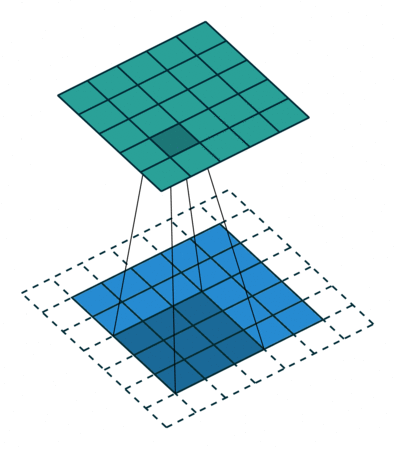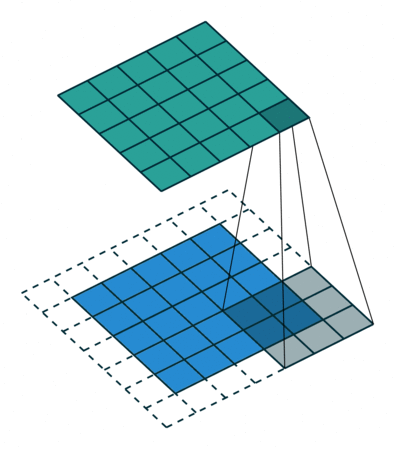 | 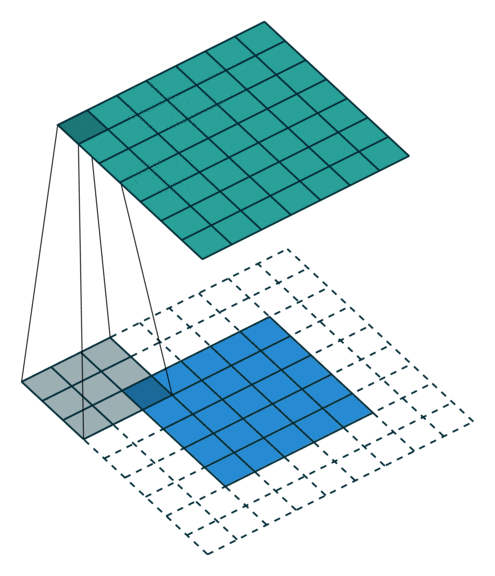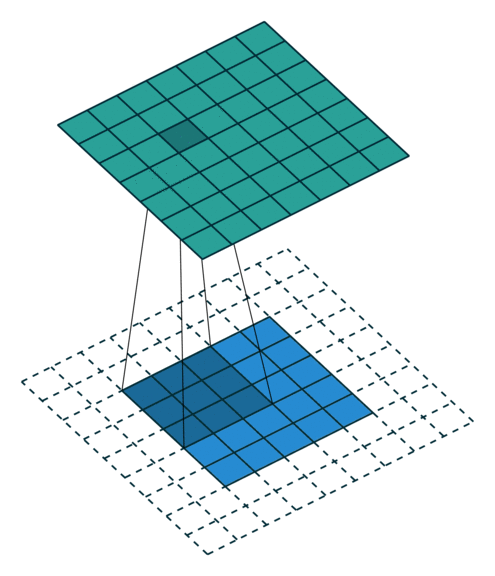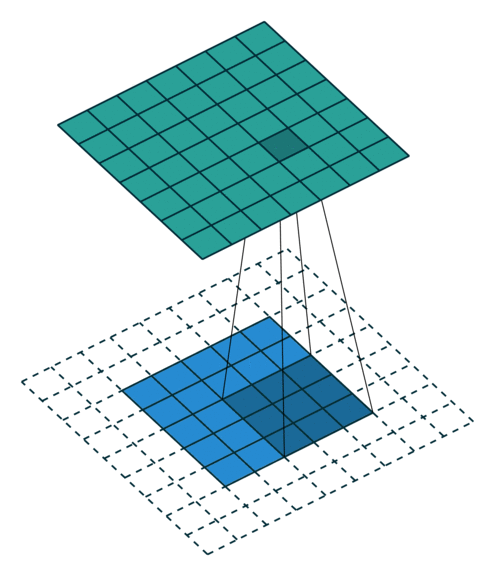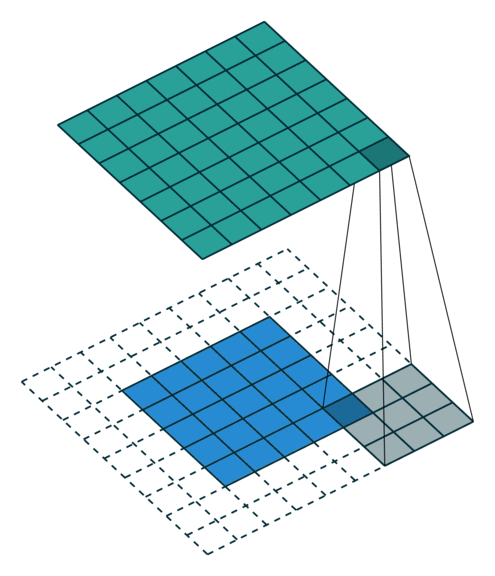 |
|---|---|---|---|
| No padding, no strides | Arbitrary padding, no strides | Half padding, no strides | Full padding, no strides |
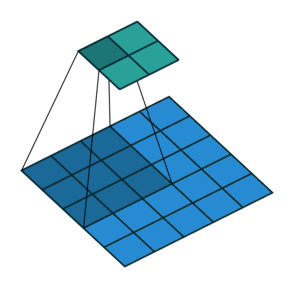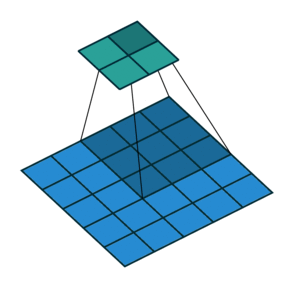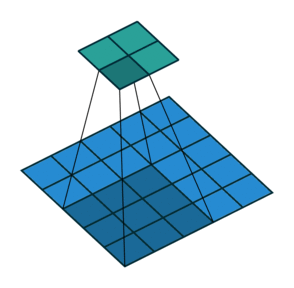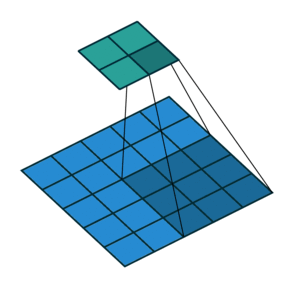 | 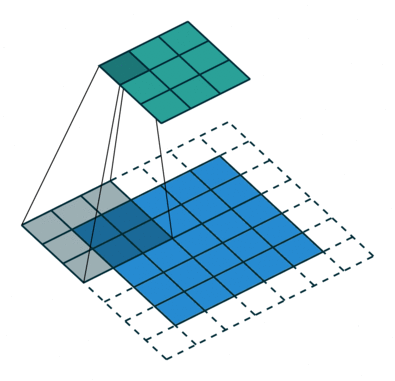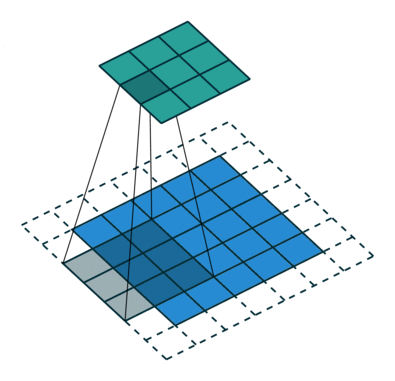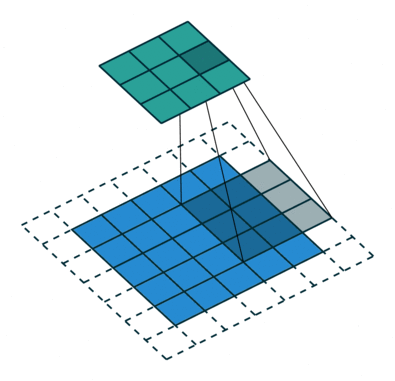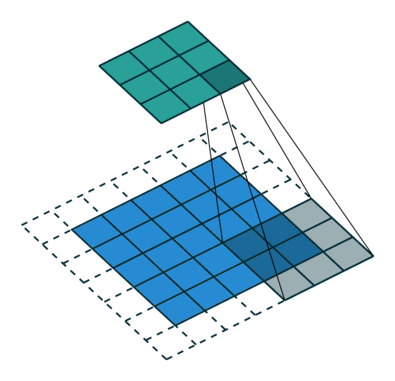 | 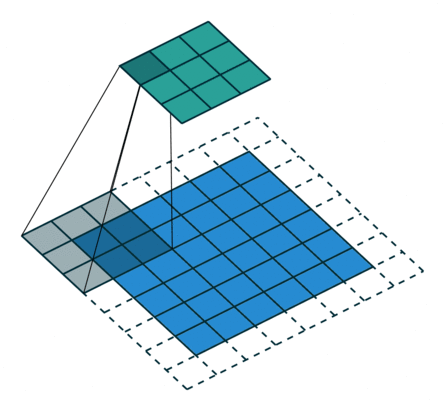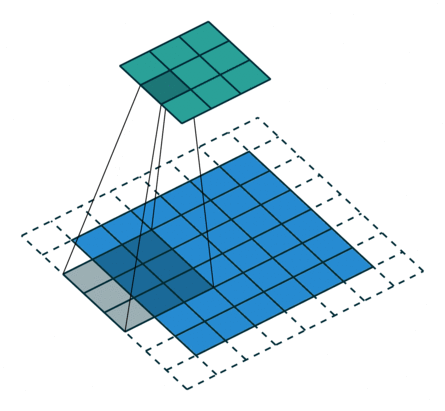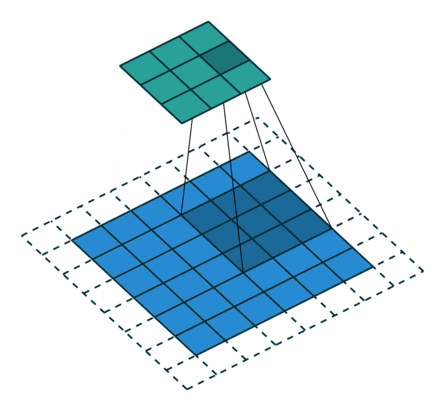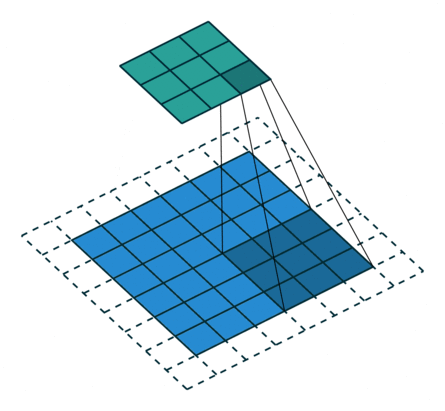 | |
| No padding, strides | Padding, strides | Padding, strides (odd) |
Transposed convolution animations
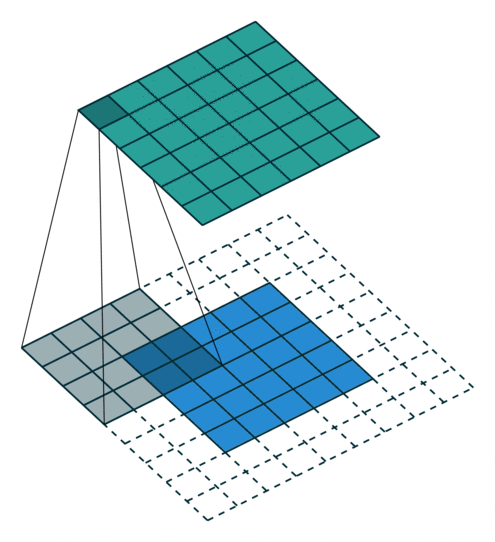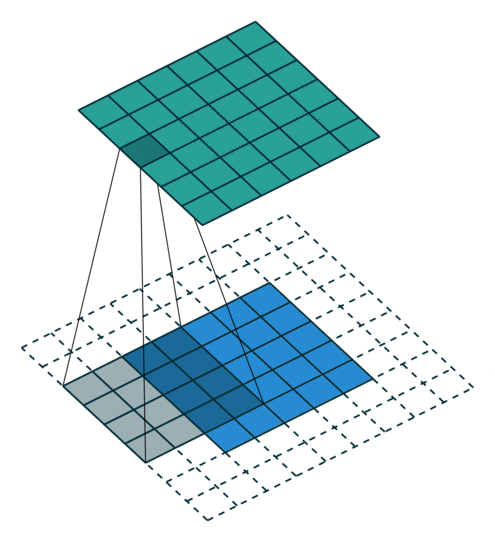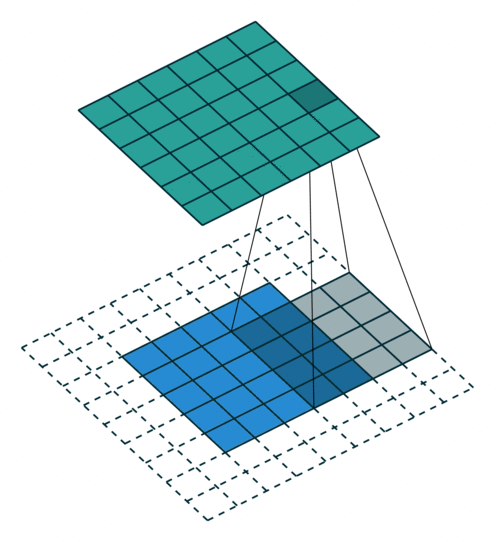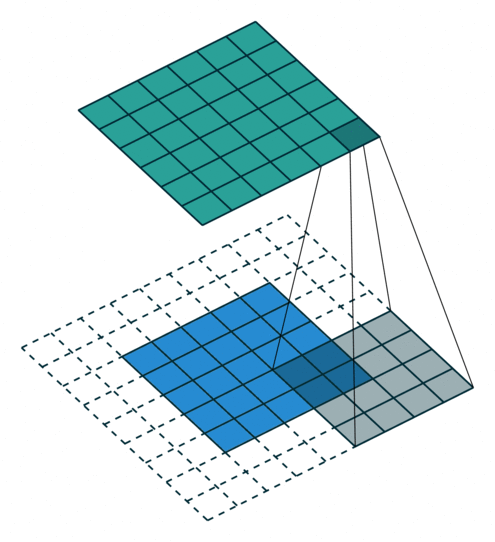
N.B.: Blue maps are inputs, and cyan maps are outputs.
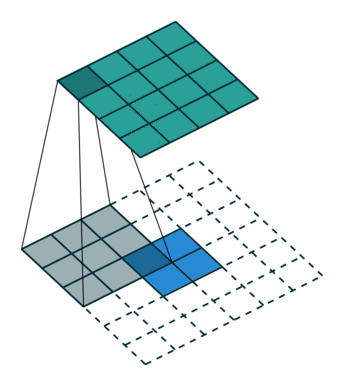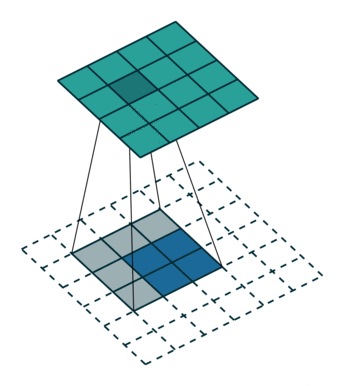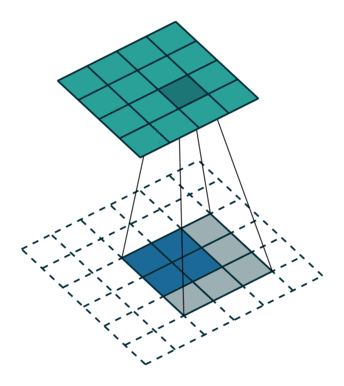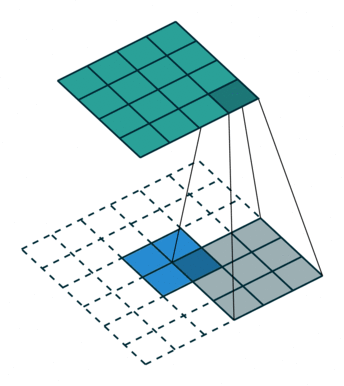 | 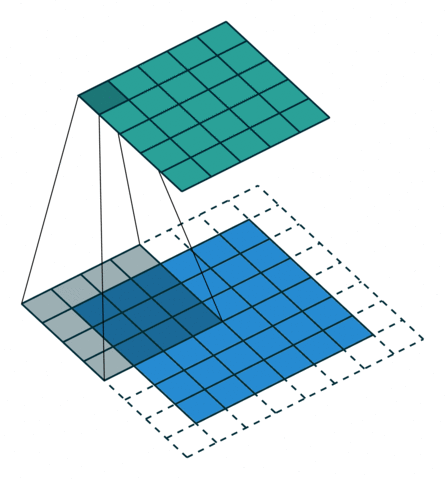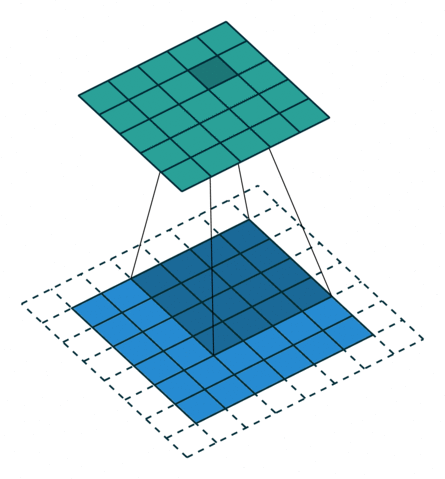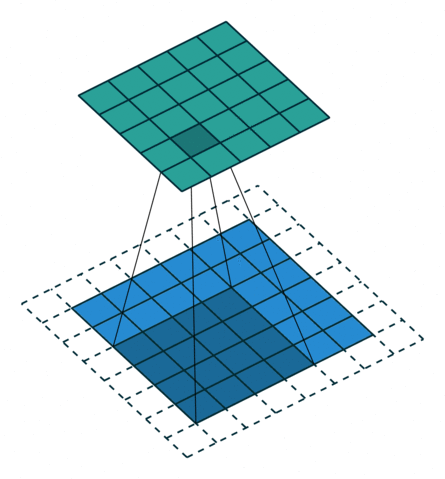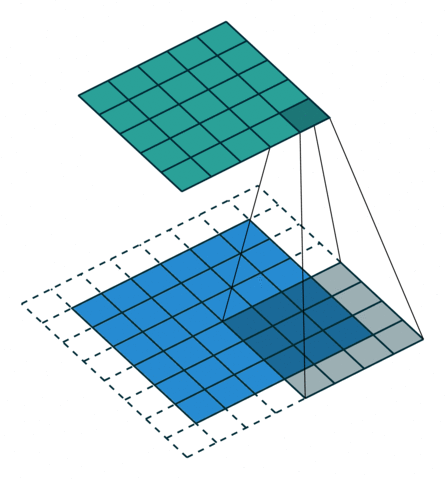 | 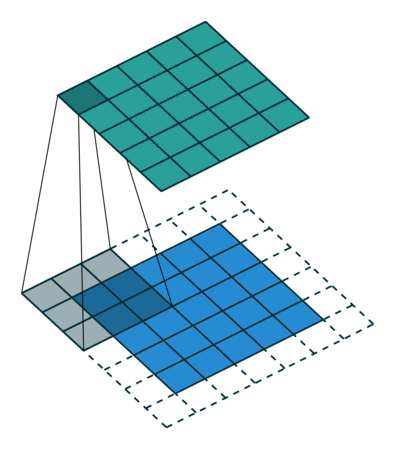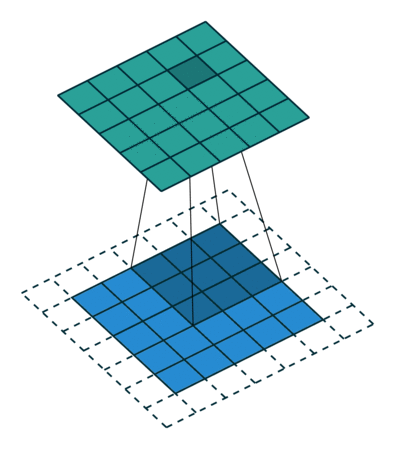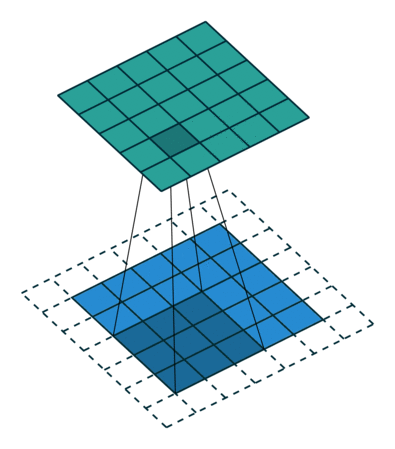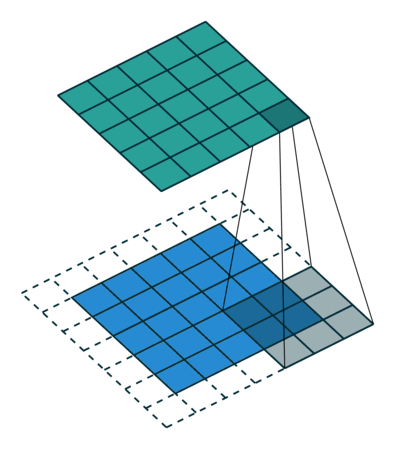 | 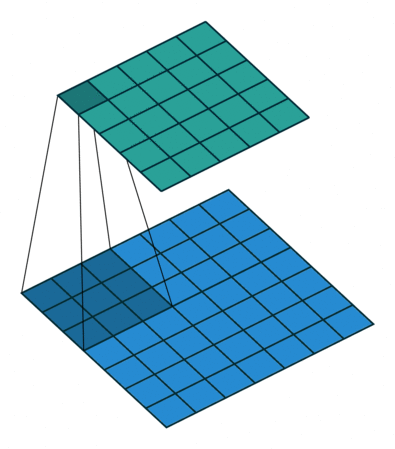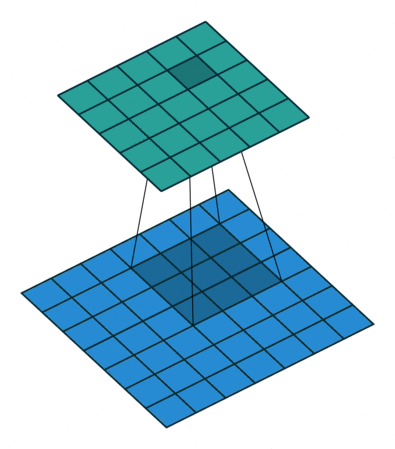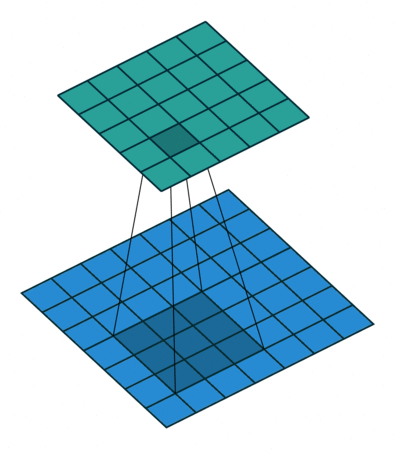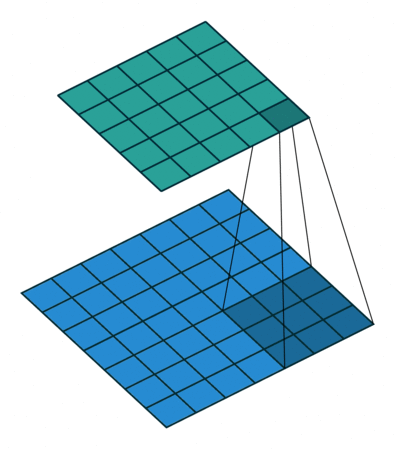 |
|---|---|---|---|
| No padding, no strides, transposed | Arbitrary padding, no strides, transposed | Half padding, no strides, transposed | Full padding, no strides, transposed |
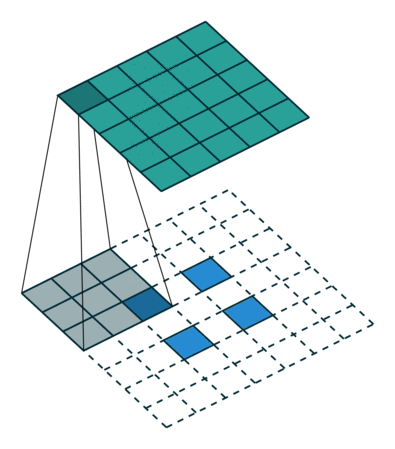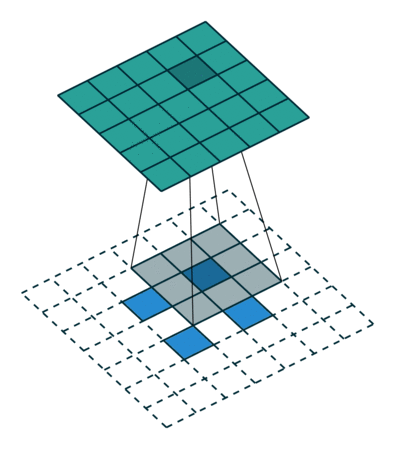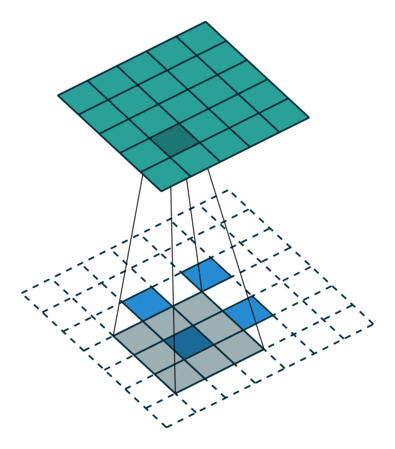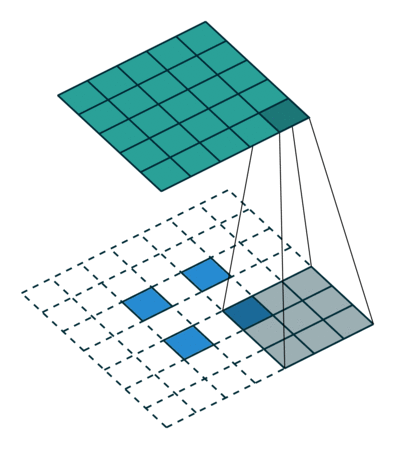 | 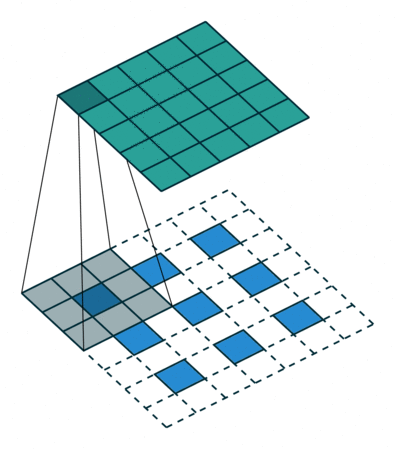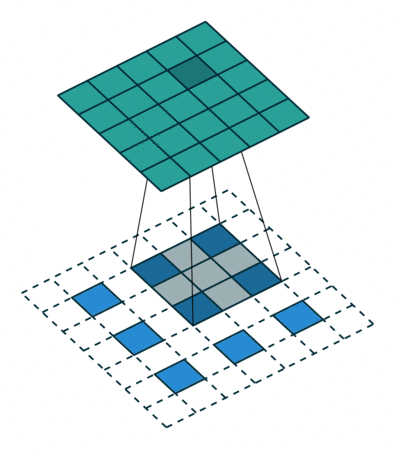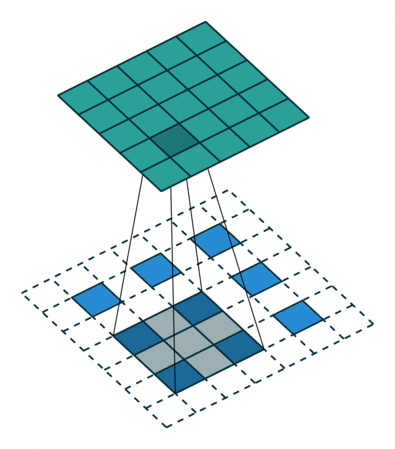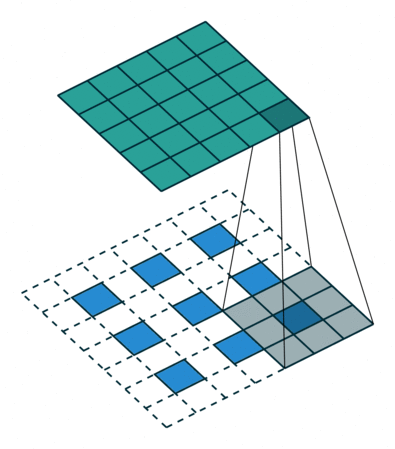 | 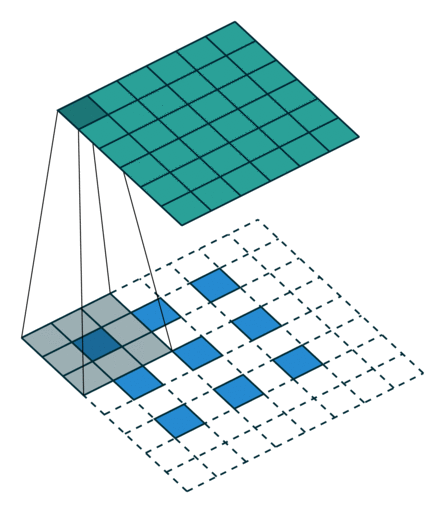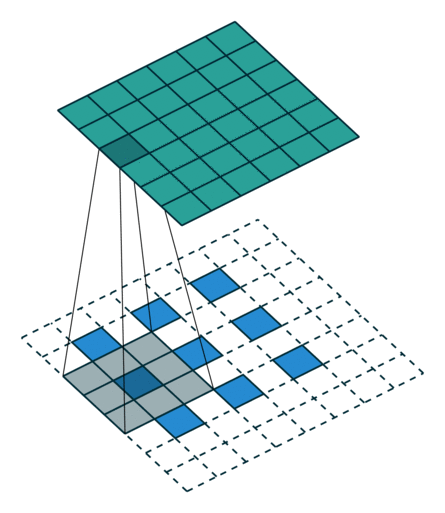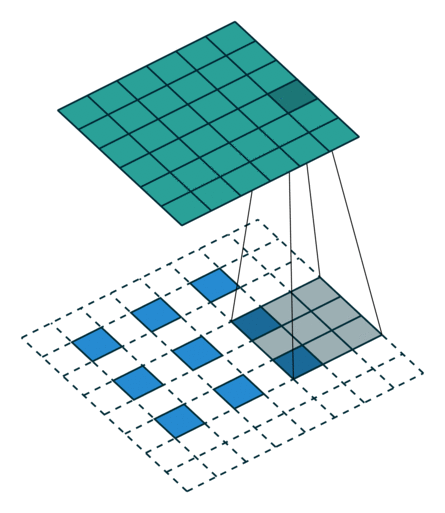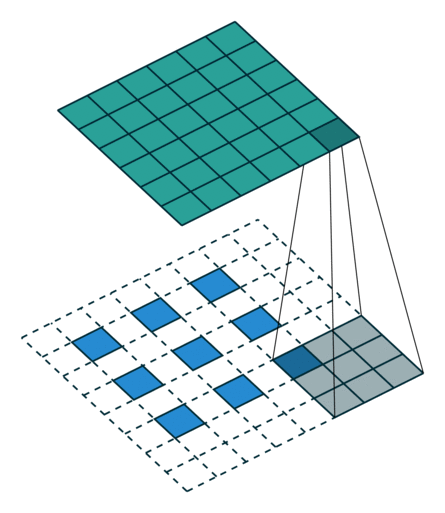 | |
| No padding, strides, transposed | Padding, strides, transposed | Padding, strides, transposed (odd) |
Dilated convolution animations
N.B.: Blue maps are inputs, and cyan maps are outputs.
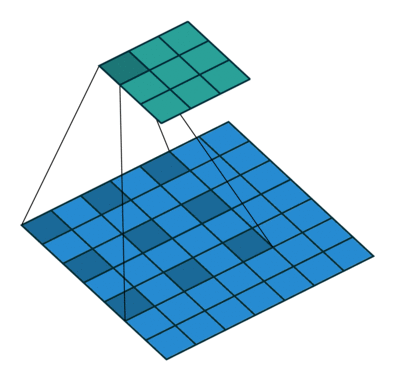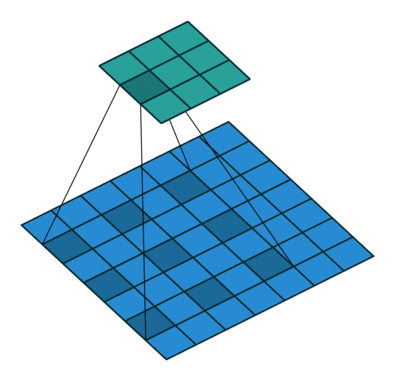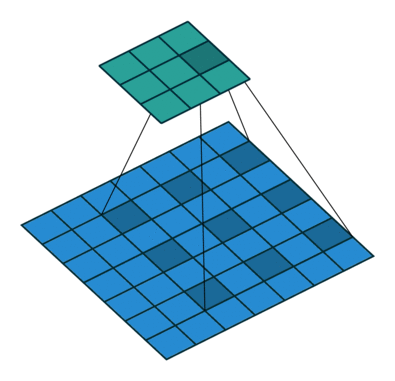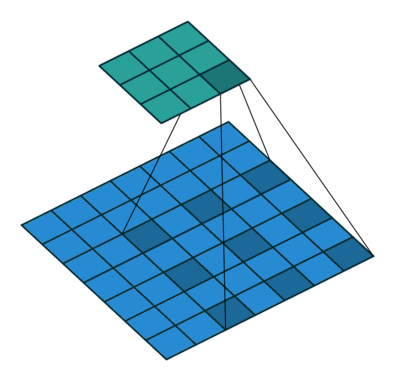 |
|---|
| No padding, no stride, dilation |
基本概念——池化、全连接
-
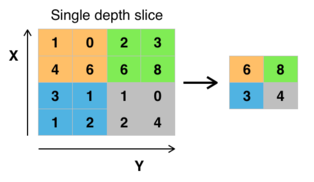
池化层
- 特殊形式卷积
- 降维、减少数据计算量,减缓过拟合,特征不变性(平移、尺度)
-
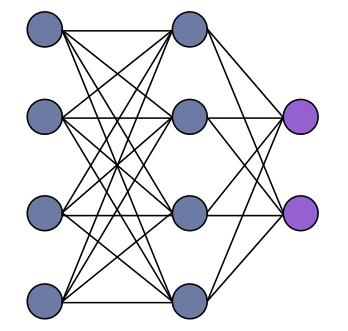
全连接层
- 模型输出层
- 分类、回归
多层卷积神经网络示例
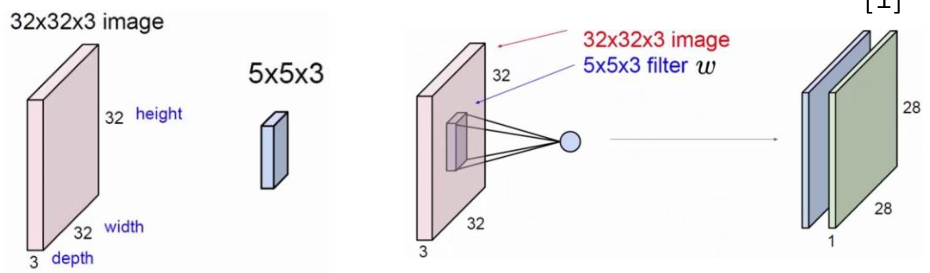 | 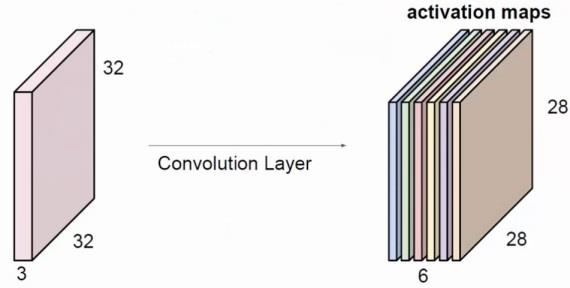 | 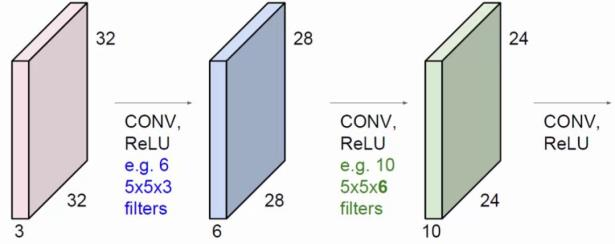 |
|---|---|---|
| 卷积核大小为5*5,步长为1,不扩充边界,输入通道为3,输出通道为2 | 输出通道数为6,其余参数不变。 | 第一层的输出通道数为3,第二层输出通道数为6。 |
卷积神经网络发展历程
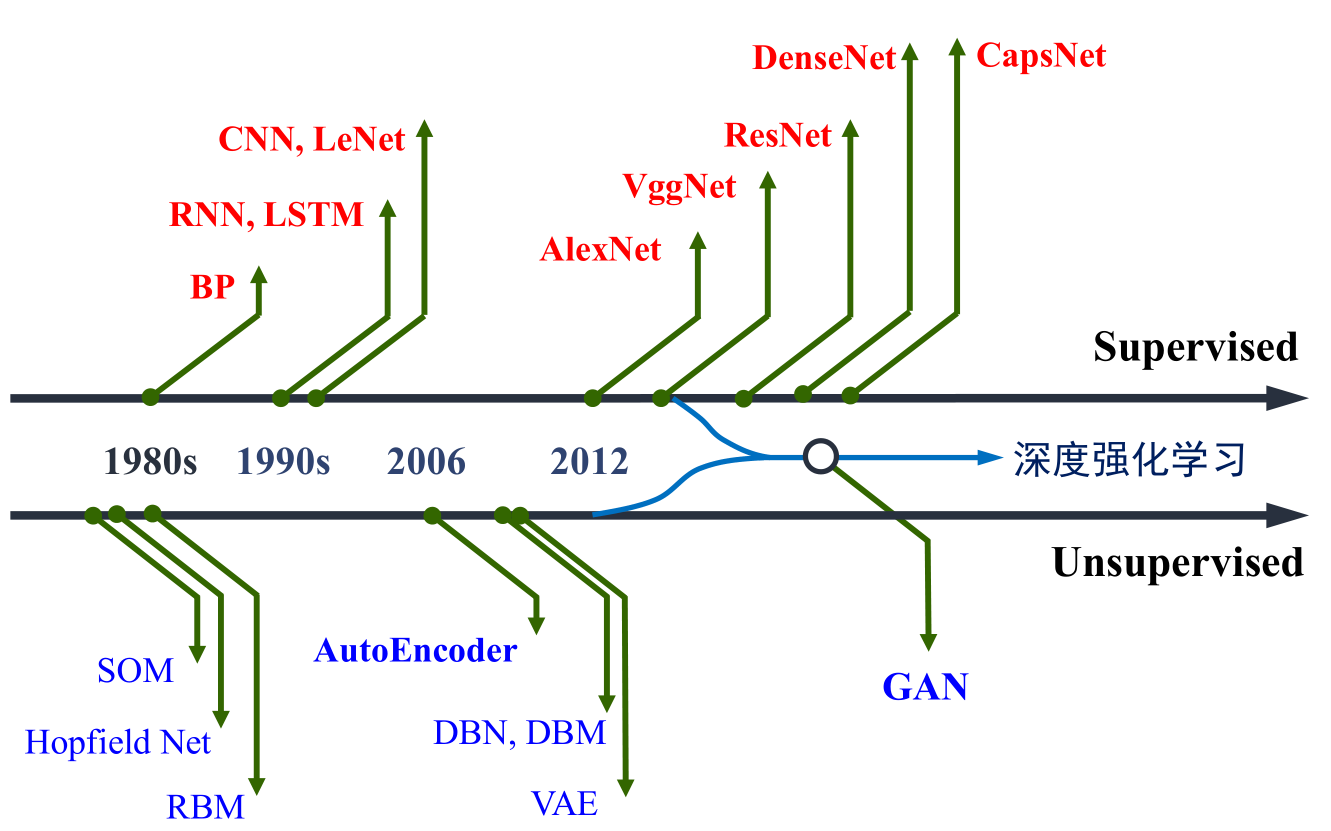
为什么能得到飞速发展:
- 数据爆炸:图像数据、文本数据、语音数据、社交网络数据、科学计算等
- 计算性能大幅提高
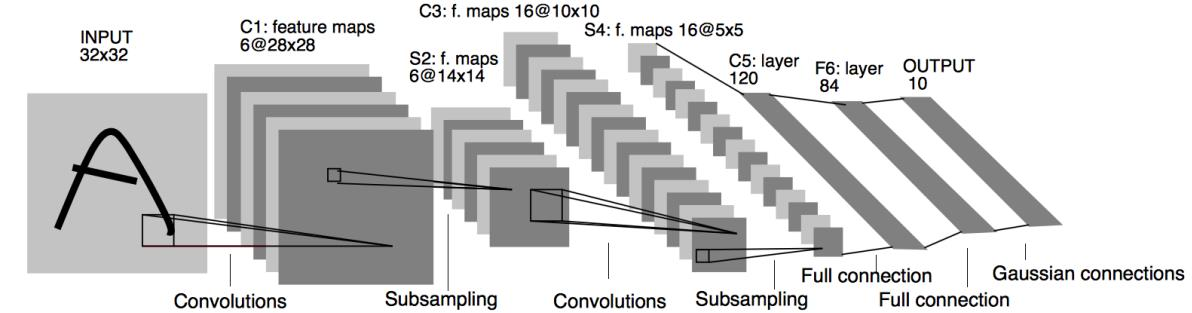
现代卷积神经网络结构基础——LeNet
- LeNet诞生于1994年,由Yann LeCun提出,用于手写字符识别与分类
- 6层网络结构:两个卷积层,两个下采样层和两个全连接层
- 卷积层包括两部分:卷积计算和sigmoid非线性激活函数
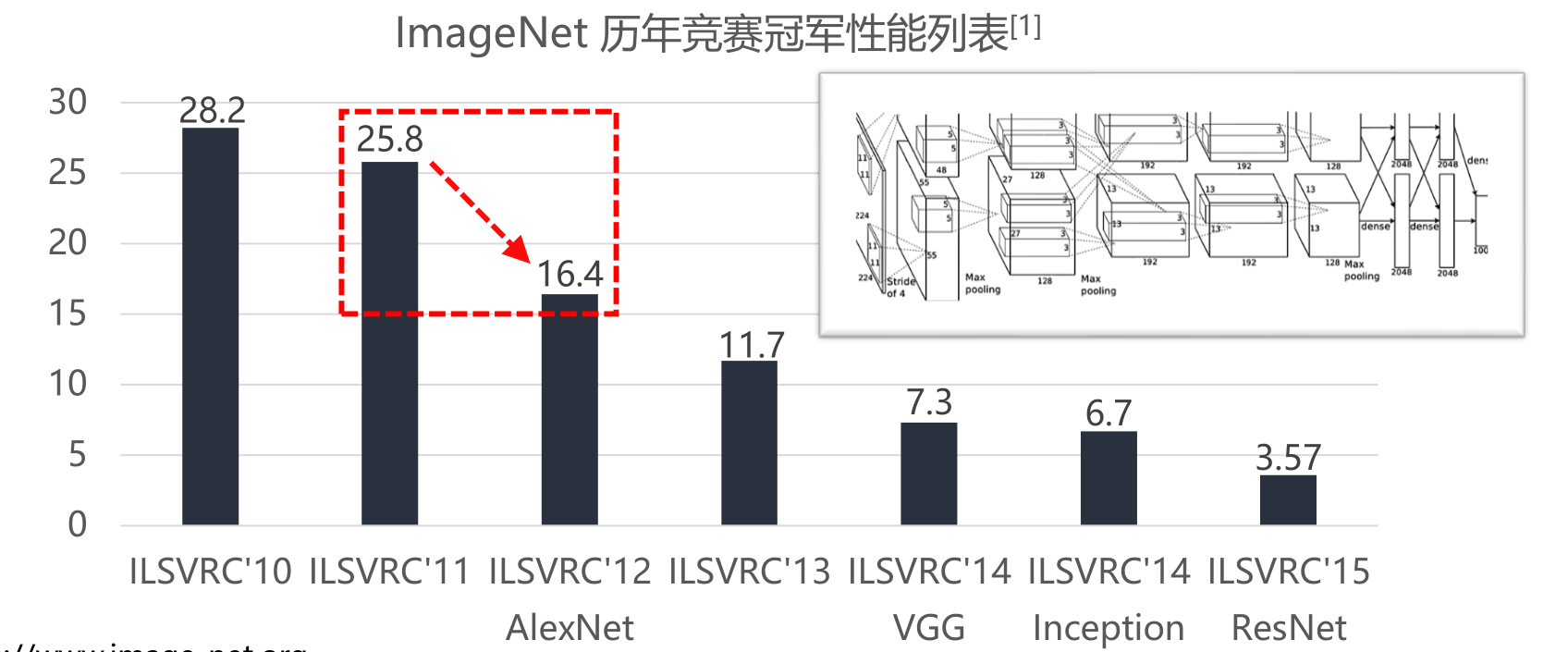
研究重心转向卷积神经网络——AlexNet、VGGNet
- 网络更深:AlexNet一共8层,VGGNet一共16层或19层
- 数据增广:为增强模型泛化能力,对256×256原始图像进行随机裁剪,得到尺寸为224×224图像,输入网络进行训练
- ReLU非线性激活函数:减少计算量,缓解梯度消失,缓解过拟合。ReLU激活函数现已成为神经网络中最通用的激活函数
- Dropout:全连接层神经元以一定概率失活,失活神经元不再参与训练。Dropout的引用,有效缓解了模型的过拟合
- Pre-Training:先训练一部分小网络,确保稳定之后,在此基础上网络逐渐加深。
卷积神经网络深度、宽度扩展—— GoogLeNet
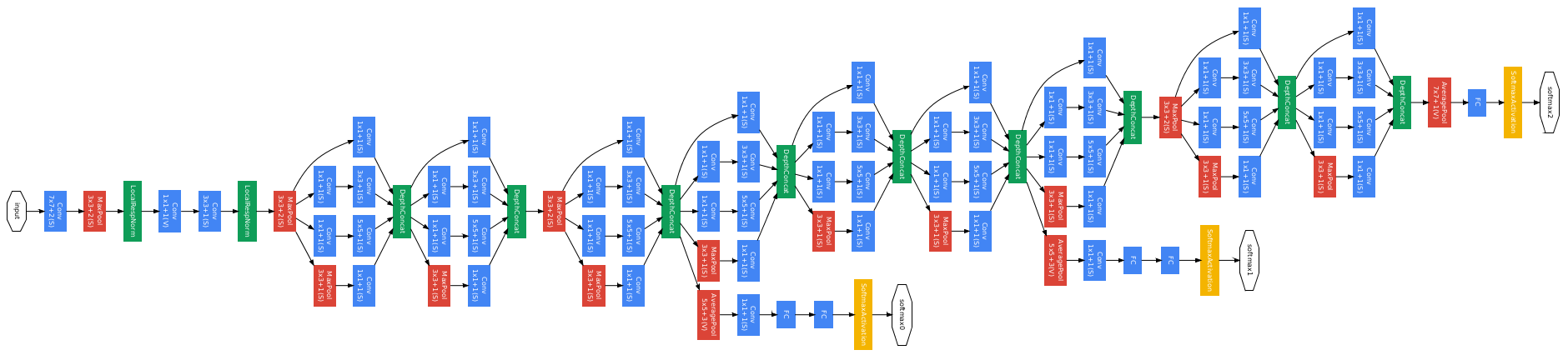
- 网络更深:GoogLeNet一共22层
- 多分辨率结构:引入Inception结构替代传统卷积+激活
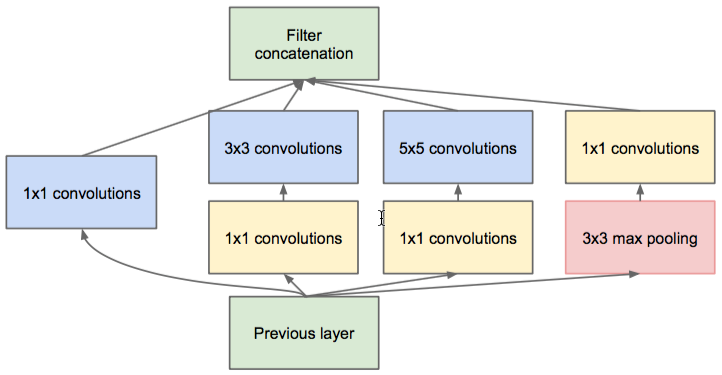
- 计算量降低:采用1×1卷积核来实现数据降维
Inception 结构
GoogLeNet 结构
卷积神经网络深度、宽度再扩展—— ResNet、DenseNet
- 网络更深:ResNet已超过一百层(ResNet-101)
- 残差连接:特征经两条路线传递,常规路线与捷径
- 跳跃连接:底层特征与高层特征相融合
| ResNet残差连接示意图 | DenseNet结构示意图 |
|---|---|
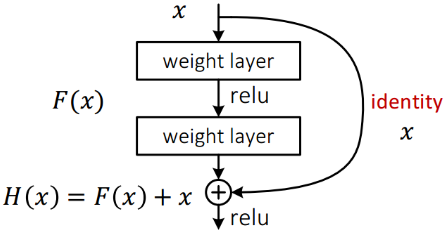 | 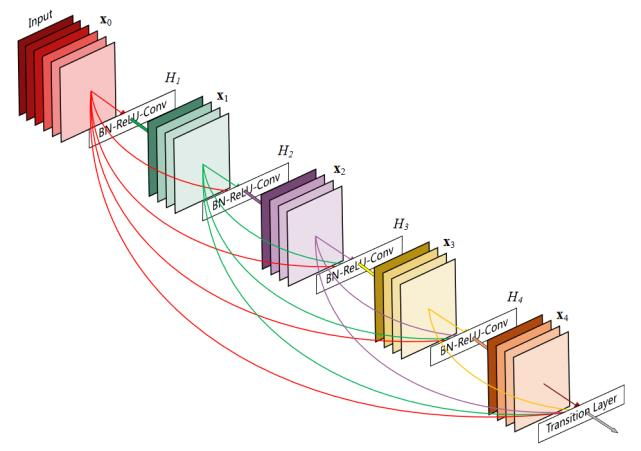 |
卷积神经网络通用性扩展
- 深度可分离卷积
- 5×5分通道卷积
- 1×1卷积融合各通道特征
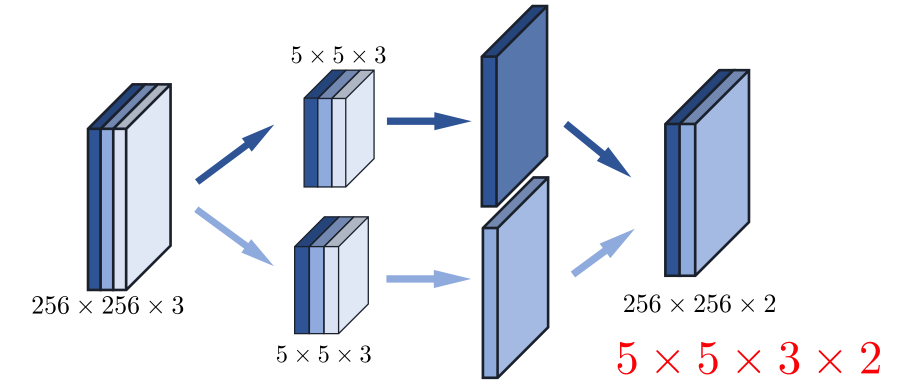
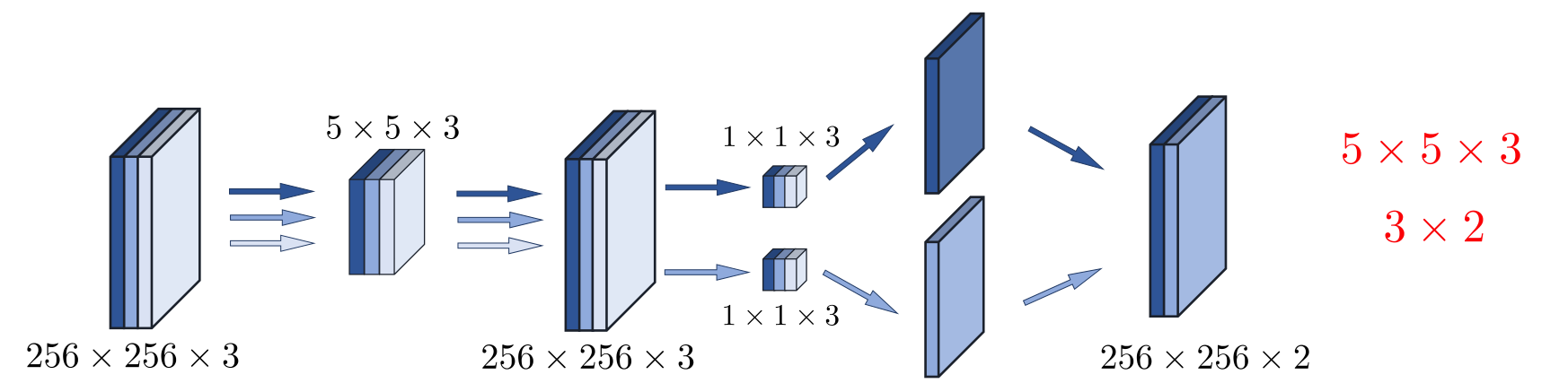
- 空洞卷积(膨胀卷积)
- 局部输入不变
- 感受野变大
| 空洞卷积感受野 | 空洞卷积计算过程 |
|---|---|
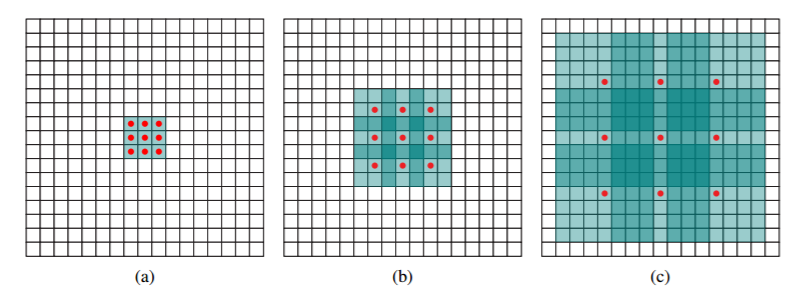 |  |
卷积神经网络计算范式
- 多维欧式空间
- 局部空间响应
- 卷积参数共享
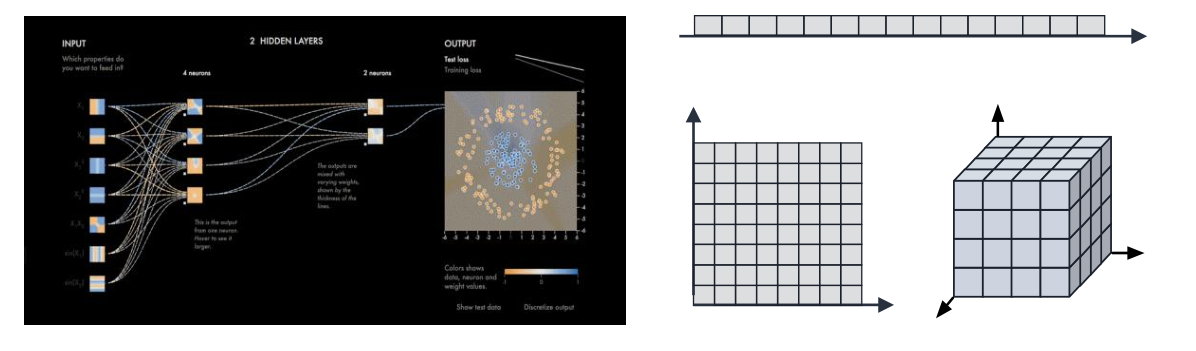
卷积神经网络拓展至非欧空间
欧式空间非规则化连接—活性卷积
- 活性卷积 (CVPR 2017)
-
双线性插值:离散坐标下,可以通过插值方法计算得到连续位置的像素值
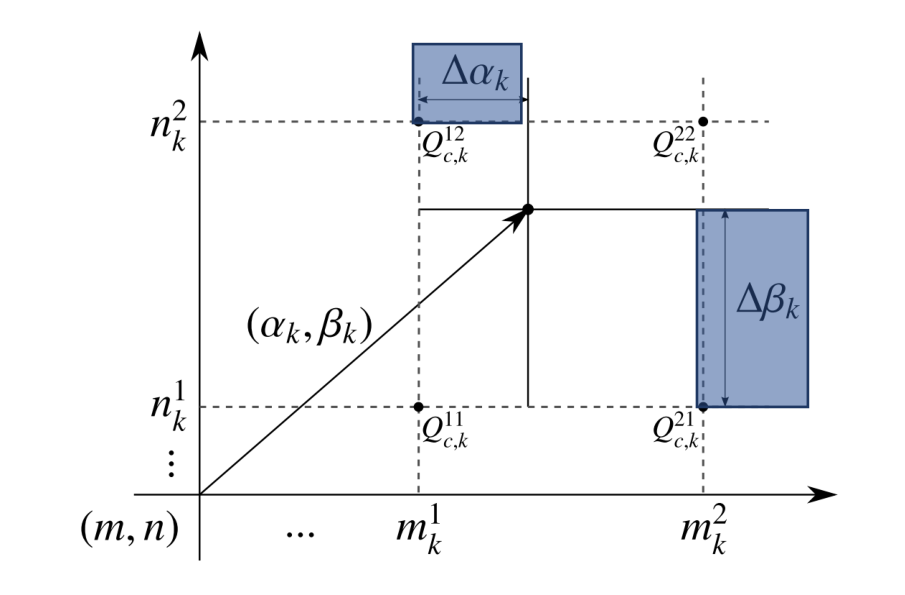
-
可学习参数 △αk,△βk
-
可变卷积核形状固定
-
- 卷积核形状可变
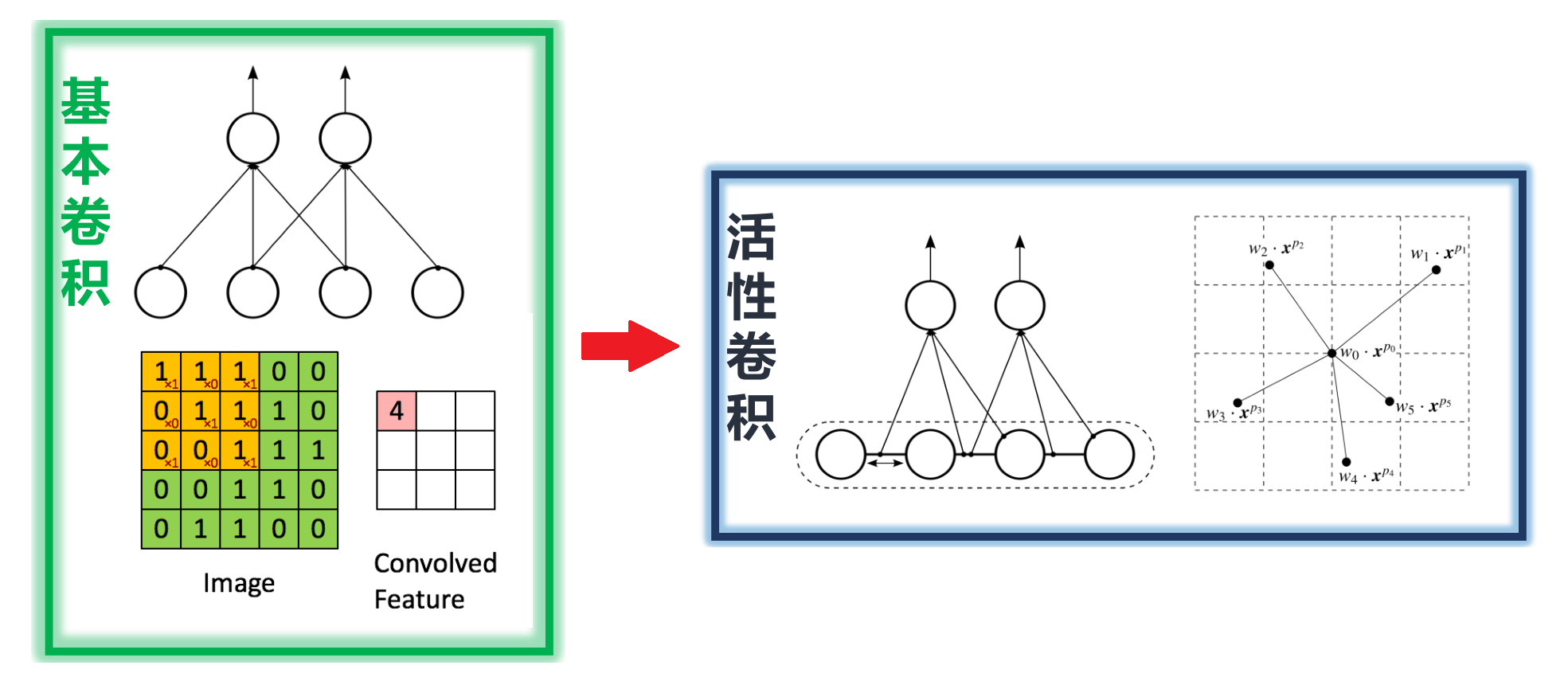
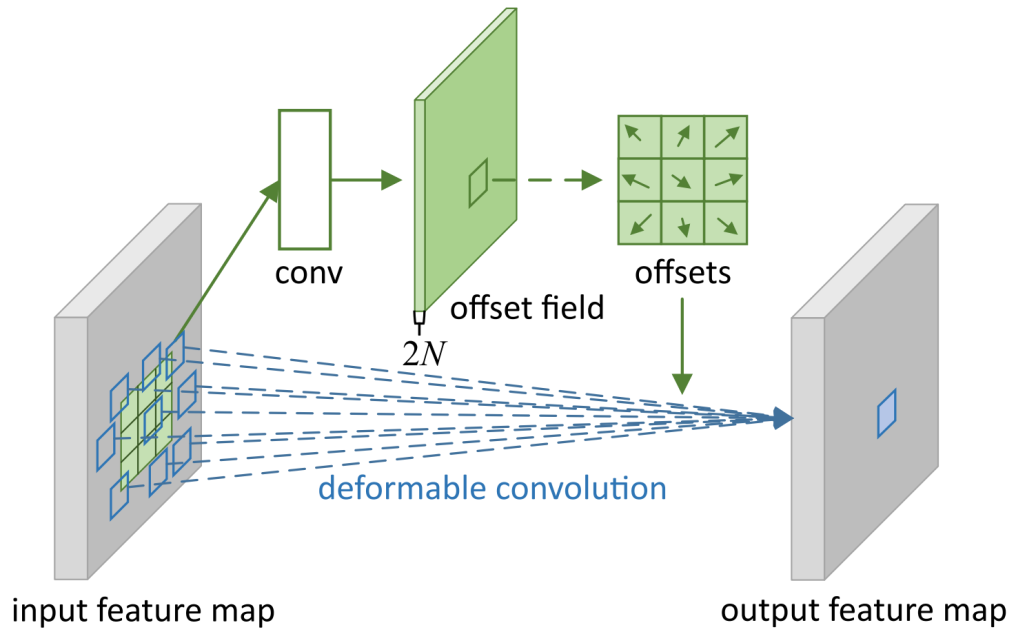
欧式空间非规则化连接—可变形卷积
-
可变形卷积 (ICCV 2017)
- 3×3 可变形卷积 (N=9)
- 每个位置对应一个偏置
- 偏置通过额外卷积学习
- 每个偏置为二维向量
-
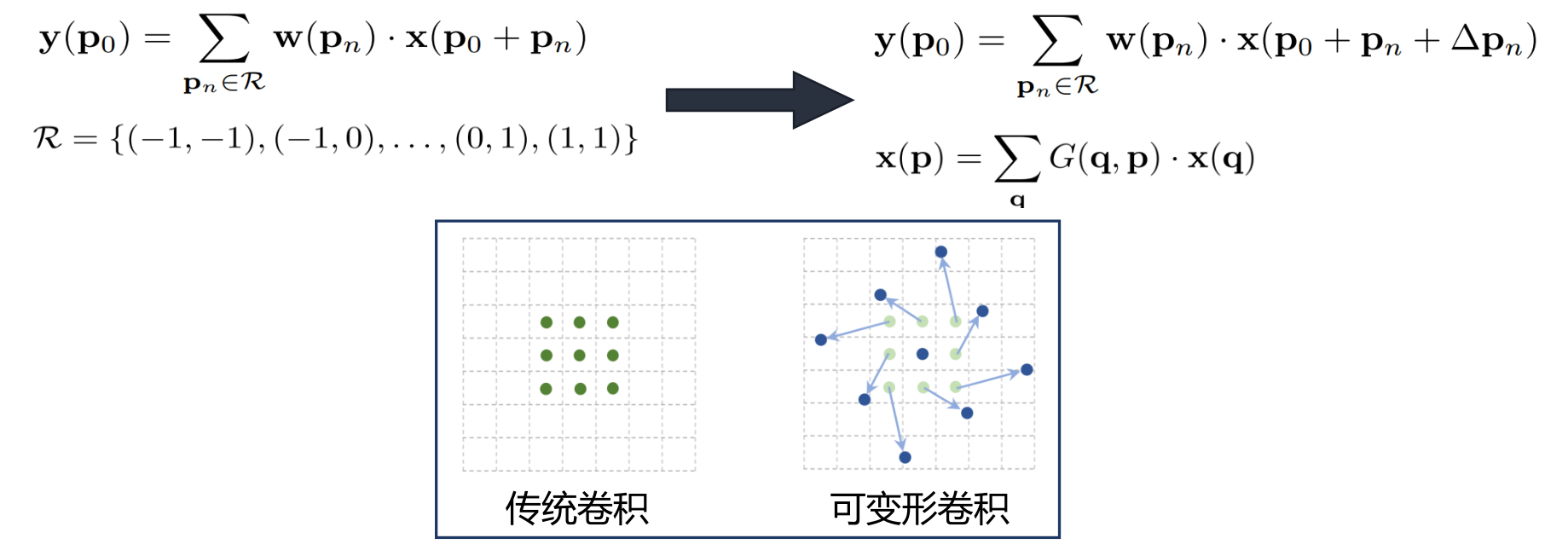
卷积核位置参数化
-
双线性插值连续化
-
传统BP算法训练
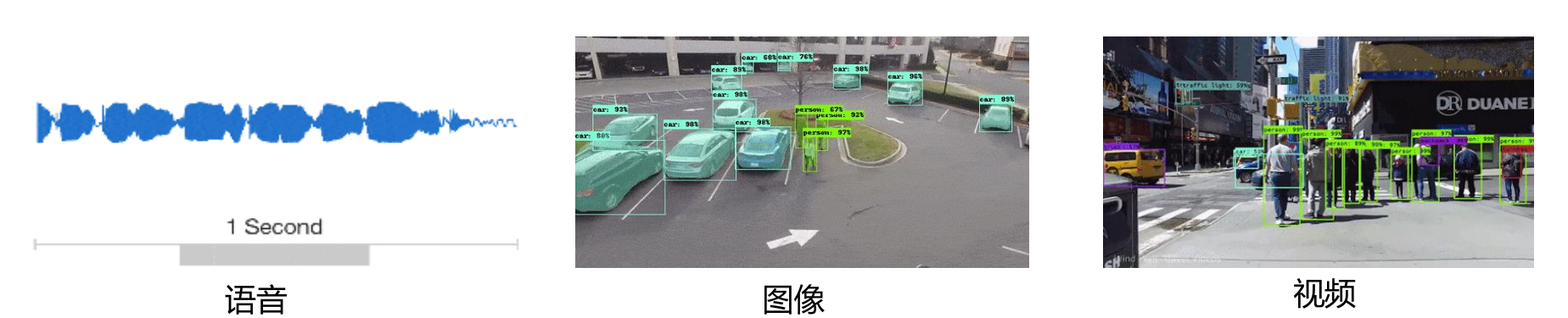
欧式空间卷积神经网络
- 处理固定输入维度数据、局部输入数据必须有序
- 语音、图像、视频(规则结构)满足以上两点要求
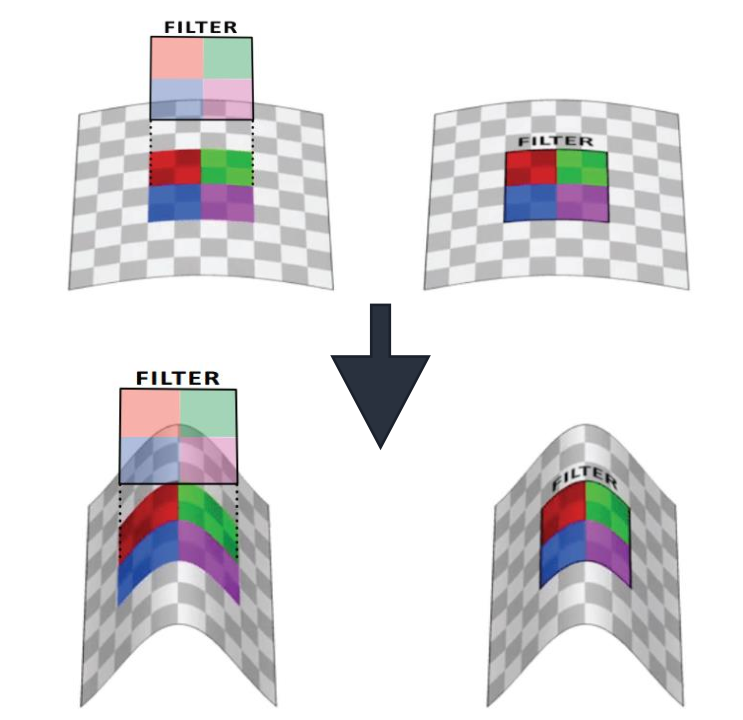
非欧式空间结构数据
- 局部输入维度可变
- 局部输入排列无序
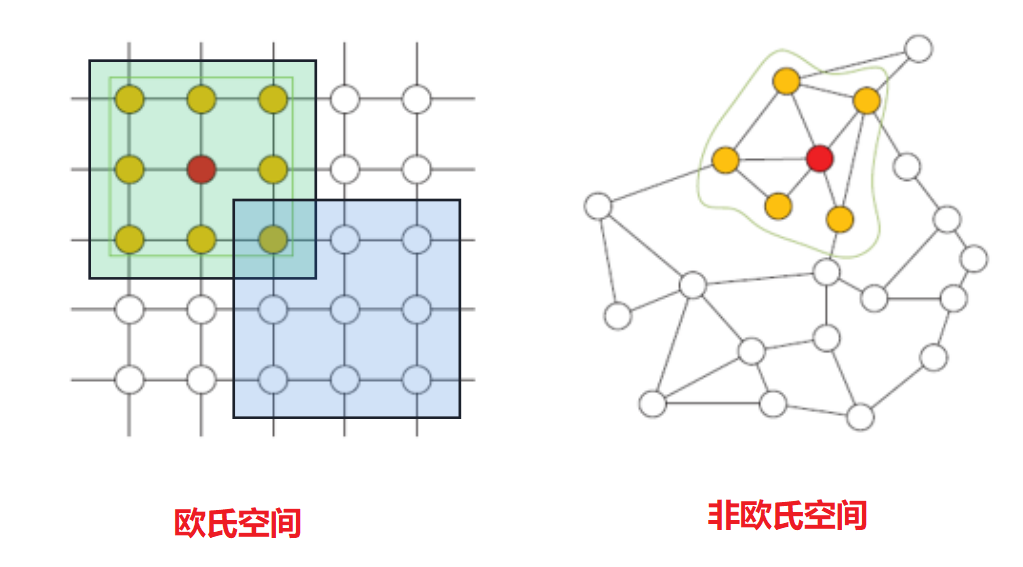
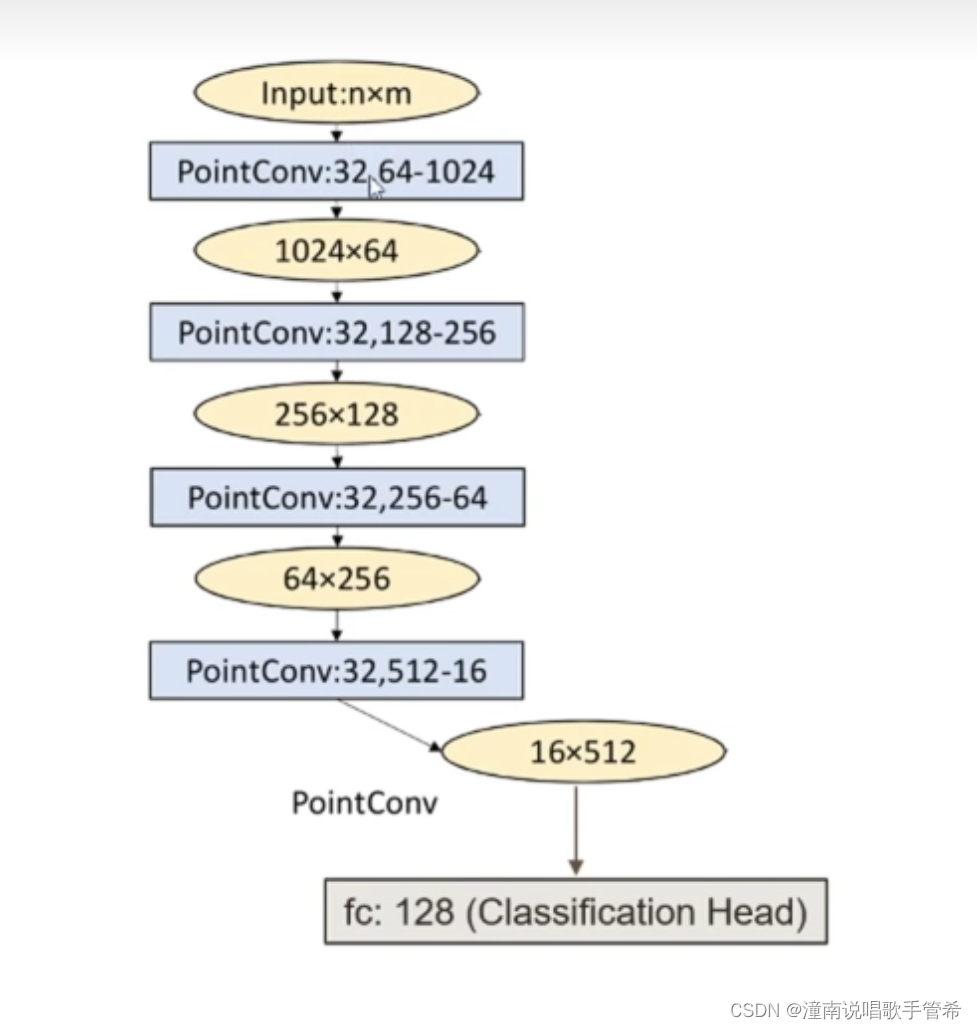
非欧式空间卷积神经网络
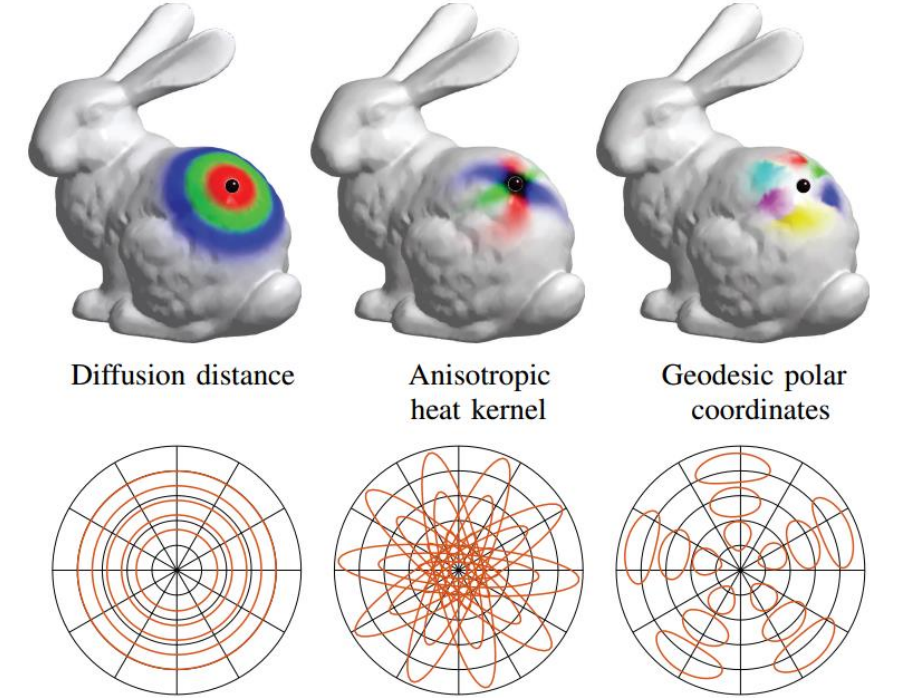
本系列内容
- 绪论,卷积神经网络:从欧氏空间到非欧氏空间(本文内容)
- 谱域图卷积介绍
- 空域图卷积介绍(一)
- 空域图卷积介绍(二)
- 图卷积的实践应用
- 基于PyTorch的图卷积代码实现
后续笔记将更新至专栏《图卷积神经网络》中。









![[Rust笔记] 规则宏的“卫生保健”](https://img-blog.csdnimg.cn/img_convert/c3bf7a8936a48cb0e53e80e93cf1d079.png)