前言：
大家好，我是良辰丫🪐🪐🪐，在探索数据结构的旅程中，二叉树可以说是数据结构中的重点，笔试面试经常出现的问题，同时也是难点。🐥🐥🐥不要看到难就感觉到畏惧，多去刷题，多去感悟，其实一切没大家想的那么难。我们接下来去探索二叉树的海洋。🍣🍣🍣

🧑个人主页：良辰针不戳
📖所属专栏：java数据结构
🍎励志语句：生活也许会让我们遍体鳞伤，但最终这些伤口会成为我们一辈子的财富。
💦期待大家三连，关注，点赞，收藏。
💌作者能力有限，可能也会出错，欢迎大家指正。
💞愿与君为伴，共探Java汪洋大海。

---

---

1、树

树是人们日常生活中常见的，我在网上找了一个苹果树，简单的看一下树的结构，有根，有分枝，有叶子等。

接下来我们先简单了解一下树形结构。

1.1 树型结构

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

• 有一个特殊的结点，称为根结点，根结点没有前驱结点。
• 除根结点外，其余结点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm，其中每一个集合Ti (1 <= i <=m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继。
• 因为树很复杂，从根到节点，普通方法难以描述，因此我们往往采取递归的定义方法。

下面就是一个简单的树结构，每个根节点可以有多个分支，例如D作为父亲节点的时候，有三个孩子节点，G,H,I。

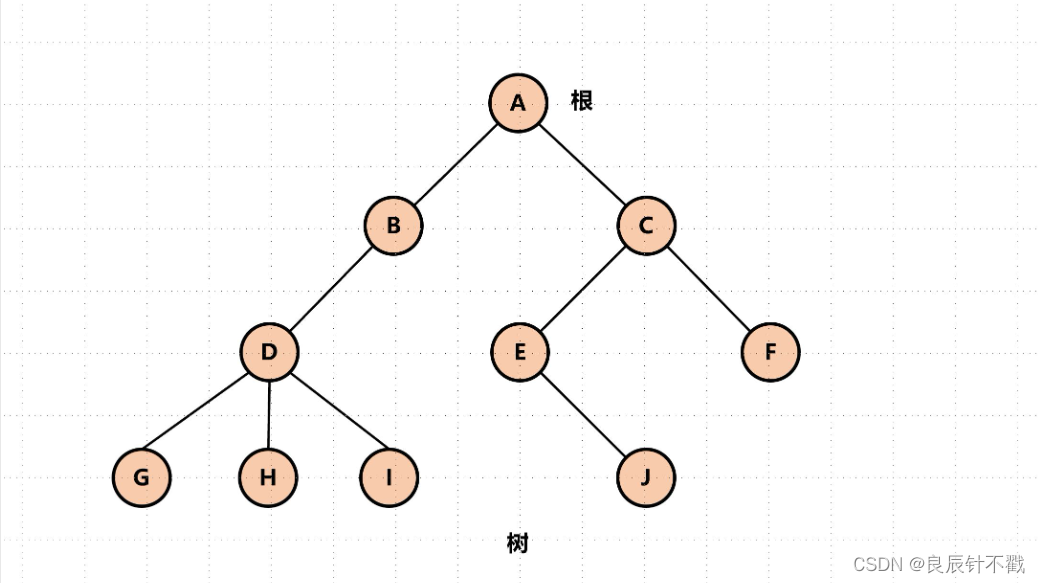
1.2 非树

如下图，A的孩子节点C和D连在一起，这种形成封闭式的图形就不是树形结构。

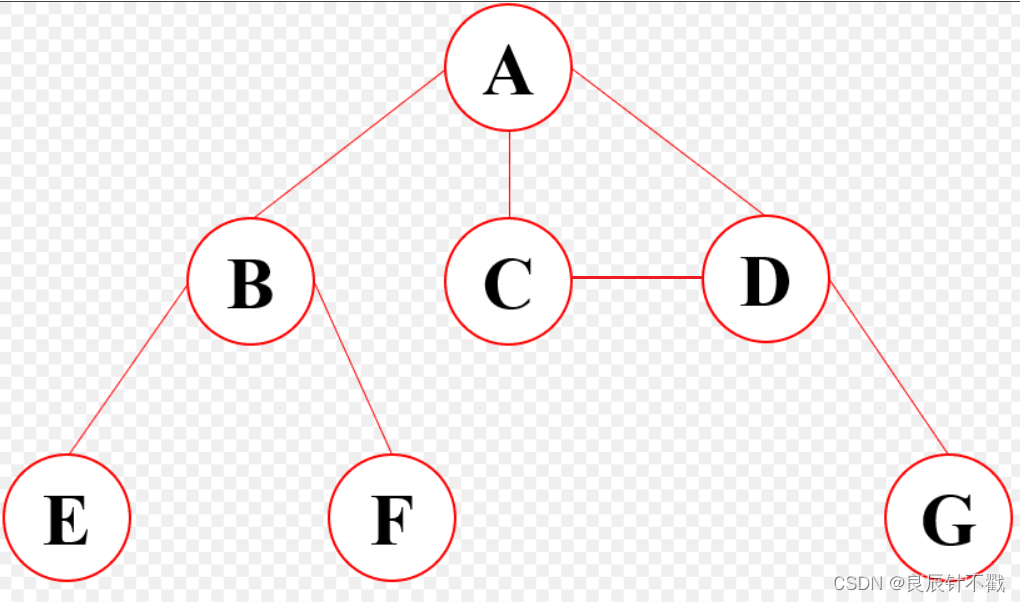
那么什么是树呢？

• 子树不能相交（不能形成封闭图形）。
• 除了根节点外，每个节点只有一个父亲节点。
• 一个n个节点的树有n-1条边。

1.3 树的相关概念

在学习树形结构的时候，我们需要去了解相关概念，不对，是掌握相关概念，真正深入了解了相关概念，才能灵活快速的去写出所谓好的代码，嘿嘿嘿。

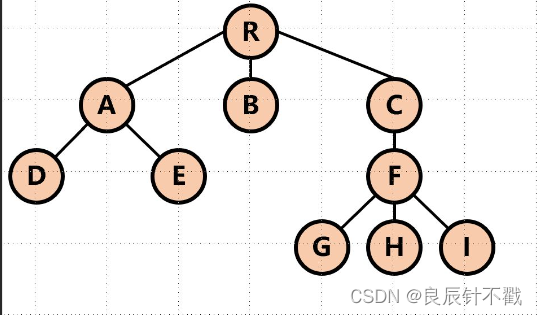
1. 结点的度：一个结点含有子树的个数称为该结点的度； 如上图：A的度为3。
2. 树的度：一棵树中，所有结点度的最大值称为树的度； 如上图：树的度为3。
3. 叶子结点或终端结点：度为0的结点称为叶结点； 如上图：D、E、B、G…等节点为叶结点
4. 双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点； 如上图：R是A的父结点。
5. 孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点； 如上图：B是R的孩子结点
6. 根结点：一棵树中，没有双亲结点的结点；如上图：R。
7. 结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推，上图中D的层次为3。
8. 树的高度或深度：树中结点的最大层次； 如上图：树的高度为4。
9. 非终端结点或分支结点：度不为0的结点； 如上图：A,C…等节点为分支结点。
10. 兄弟结点：具有相同父结点的结点互称为兄弟结点； 如上图：A、B、C是兄弟结点。
11. 堂兄弟结点：双亲在同一层的结点互且父亲节点不同的几个节点为堂兄弟；如上图：D、F互为堂兄弟结点。
12. 结点的祖先：从根到该结点所经分支上的所有结点；如上图：R是所有结点的祖先。
13. 子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是R的子孙。
14. 森林：由m（m>=0）棵互不相交的树组成的集合称为森林。也就是一些树合起来成为一片森林，一棵树也是特殊的森林。

1.4 树的一些代码表现形式

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，如：双亲表示法，孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

下面是孩子兄弟法表示的一个代码块，可以有多个孩子。

class Node {
int value; // 树中存储的数据,可以是其它类型。
Node firstChild; // 第一个孩子引用
Node secondChild; // 第二个孩子引用
}

了解了这么多树的概念，想必大家对树形结构有了很深刻的认识，接下来我们就引入重点。🚀二叉树🚀。

2、二叉树

我们了解了树的一个父亲节点可以有多个分支，然而，二叉树最多只有两个分支。因此我们就可以简单的定义一下二叉树。

• 可以有空子树。
• 至少有一个父亲节点有两个孩子。
• 一个父亲节点最多有两个孩子节点。

注意：我们上述的三个条件只是作为研究二叉树的简单条件，空数，一个节点等也可以认为是二叉树。

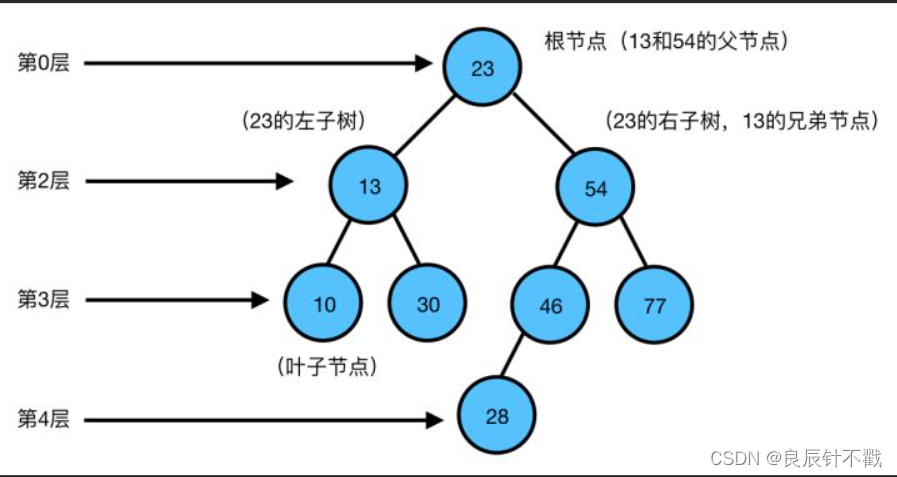
2.1 两种特殊的二叉树

2.1.1 满二叉树

满二叉树: 一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵二叉树的层数为K，且结点总数是 ，则它就是满二叉树。

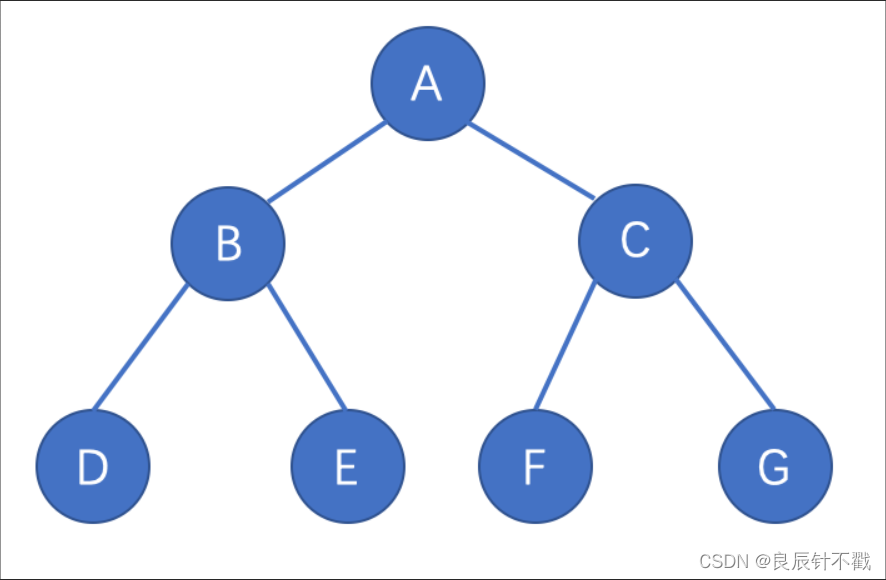
2.2.2 完全二叉树

完全二叉树: 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

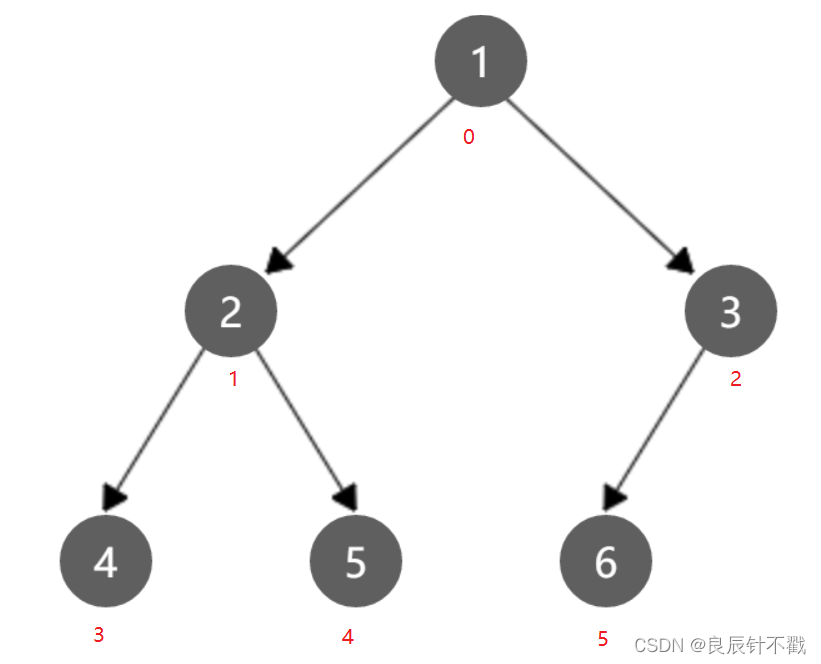
也许看了上面的图对完全二叉树的概念还有点模糊，没关系，咱们举一个反面例子。下面的图3号位置和6号位置没有数据，最后一个数据为E，所在位置为5，1~5中间的位置其中3号位置为空，那么该二叉树就不是完全二叉树，如果找到了最后一个位置，依次编号后，从第一个节点到最后一个节点中间没有空缺位置，那么这个二叉树就是一个完全二叉树。

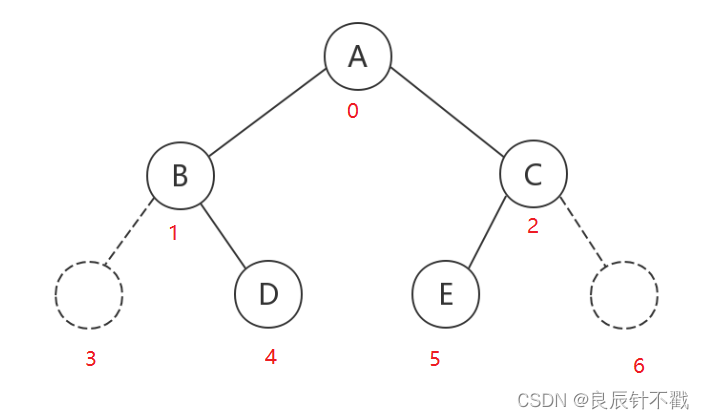
现在是不是对完全二叉树的概念有了深刻的理解了呢？既然这样，那么我们就去探索一下二叉树的性质吧。

2.3 二叉树的性质

1. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有 (i>0)个结点。
2. 若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是 (k>=0)。
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1。
4. 具有n个结点的完全二叉树的深度k为 上取整。
5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i的结点有：
   若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点。
   若2i+1<n，左孩子序号：2i+1，否则无左孩子。
   若2i+2<n，右孩子序号：2i+2，否则无右孩子。

2.4 二叉树的代码表示

二叉树有很多代码表示形式，在这里我们选择最常用的链式存储中的孩子表示法。既然有链式存储，也会有顺序存储，在后面我们学到了堆的时候再具体介绍。

class Node {
int val; // 数据域
Node left; // 左孩子
Node right; // 右孩子
}

3、二叉树的遍历

二叉树常用的遍历方式有三种。

• 前序遍历
• 中序遍历
• 后序遍历

3.1 前序遍历

根节点 → 左子树 → 右子树

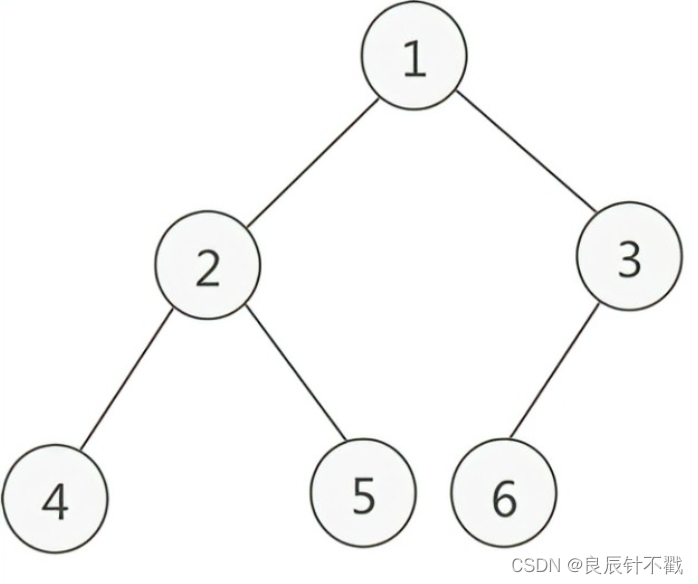
上图的前序遍历顺序为：124536
刚开始有点小伙伴可能有些不理解，大家只要记住，把父亲节点的左树当成一个整体，右树当成一个整体。

• 前序遍历先遍历根，那么先打印1。
• 然后遍历左树，左树的根为2，打印2。
• 接着遍历2的左树，打印4。
• 4的左树为空，回退到4,4的右树为空，再回退，回退到2说明2的左树打印完了。
• 最后打印2的右树，打印5。
• 5的左树和右树为空，进行回退，回退到1的时候，说明1的左树打印完了。
• 打印3，此时3作为根节点。
• 3的左树为6，打印6。
• 6的左树和右树为空，那么进行回退操作，回退到3的时候发现3的右树为空。
• 继续回退，此时回退到根节点1的时候说明打印完了。

3.2 中序遍历

左树 → 根节点 → 右树

上图的中序遍历顺序为：425163
和前序遍历的方法基本一样，只不过顺序变了而已。

1. 从根出发，寻找左树的叶子节点，4的左右子树为空，打印4。
2. 回退到2,2作为4的父亲节点，打印2。
3. 2的右树为5，而5的左右子树都为空，直接打印5。
4. 此时进行回退，回退到1时打印1。
5. 这个时候，1的左树打印完了，根节点1也打印了，进行右树操作。
6. 走到3时，找左树，3的左节点为6，而6的左右节点都为空，那么直接打印6。
7. 回退到3打印3。
8. 3的右树为空进行回退，回退到1时结束，打印完成。

3.3 后序遍历

左树 → 右树 → 根节点

上图的后序遍历顺序为：452631

1. 顺着左树走，找到了4,4作为根节点，左右子树都为空，打印4。
2. 回退到2,2的右树为5,5的左右子树都为空，直接打印5。
3. 此时回退到2，打印2。
4. 回退到1，此时说明左树已经遍历完了，接着遍历右树。
5. 走到3,3的左树为6,6的左右子树为空，打印6。
6. 回退到3,3的右树为空，打印3。
7. 回退到1，打印1，然后结束。

看完三种遍历方式，不知道大家是否发现了规律，无论是三种遍历的哪一种，每一个节点都要经过三次，前序遍历在经过第一次的时候打印该节点，中序遍历在经过第二次的时候打印该节点，后序遍历在经过第三次的时候打印该节点。哈哈，学习是一个探索的过程，接下来我们就要进行三种遍历的代码书写。

4、三种遍历代码实现

这里主要是递归实现，后面我会发一些非递归，慢慢来，一口不能吃成一个胖子，循序渐进，加油。

4.1 前序遍历

public void preOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

4.2 中序遍历

public void inOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

4.3 后序遍历

public void postOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val+" ");

    }

5、二叉树常见的基本操作代码

5.1 获取树中节点的个数

public int size(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftSize = size(root.left);
        int rightSize = size(root.right);
        return leftSize + rightSize + 1;
    }

5.2 获取叶子节点的个数

int getLeafNodeCount(TreeNode root) {
        if(root == null) {
            return 0;
        }
        if(root.left == null && root.right == null){
            return 1;
        }
        int leftSize = getLeafNodeCount(root.left);
        int rightSize = getLeafNodeCount(root.right);
        return leftSize+rightSize;
    }

5.3 获取第K层节点的个数

int getKLevelNodeCount(TreeNode root,int k) {
        if(root == null) {
            return 0;
        }
        if(k == 1) {
            return 1;
        }
        int leftSize = getKLevelNodeCount(root.left,k-1);
        int rightSize = getKLevelNodeCount(root.right,k-1);
        return leftSize+rightSize;
    }

5.4 获取二叉树的高度

public int getHeight(TreeNode root) {
        if(root == null) {
            return 0;
        }

        return (getHeight(root.left) > getHeight(root.right)) ?
                (getHeight(root.left)+1):(getHeight(root.right)+1);
    }

5.5 检测值为value的元素是否存在

TreeNode find(TreeNode root, int val) {
        if(root == null) {
            return null;
        }
        if(root.val == val) {
            return root;
        }
        TreeNode leftTree = find(root.left,val);
        if(leftTree != null) {
            return leftTree;
        }
        TreeNode rightTree = find(root.right,val);
        if(rightTree != null) {
            return rightTree;
        }
        return null;//没有找到
    }

5.6 层序遍历

public void levelOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            System.out.print(cur.val+" ");
            if(cur.left != null) {
                queue.offer(cur.left);
            }
            if(cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }

5.7 判断一棵树是不是完全二叉树

boolean isCompleteTree(TreeNode root){
        if(root == null) {
            return true;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            if(cur != null) {
                queue.offer(cur.left);
                queue.offer(cur.right);
            }else {
                break;
            }
        }
        while (!queue.isEmpty()) {
            TreeNode tmp = queue.poll();
            if(tmp != null) {
                return false;
            }
        }
        return true;
    }

后序：
一个二叉树写了很久，嘿嘿嘿，手有点酸，但是内心还是蛮开心的，自己在写博客的过程中也了解到一点细节，今天的自己又学到了一些知识，加油，未来可期。⛽⛽⛽