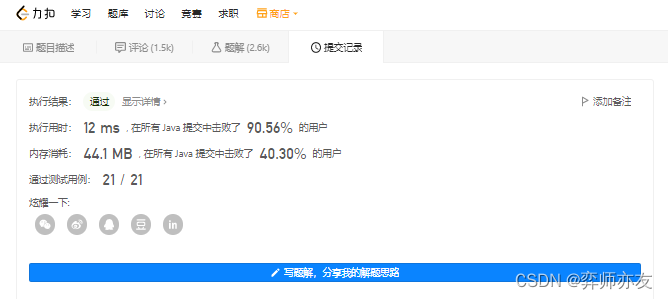
239 滑动窗口最大值

看完题后的思路

这是一道典型的单调队列的题，如果不是之前刷过一遍，对这道题没有一点头绪。即使刷过，也只是留了个印象。

解题思路

对于本道题来说，到窗口右移，如果一个新元素a进入窗口，a同时进入队列，为什么a会前方比它小的元素挤出队列呢？因为入队意味着 （1）我已经进入窗口了 （2）队列中前面比我小的元素在我如窗口后一定不会有机会再成为最大元素了，且它们一定先于我出队 所以这些元素可以出队
出队意味着：
（1）我还在窗口中，但我一定不可能成为最大元素了 （2）我即将不在窗口中了（此时我前面一定没有元素了）
步骤为：
出窗口元素出队（如果在队首的话）–>如窗口元素入队–>输出队首元素

代码

   class DandiaoQueue{
            private Deque<Integer> deque=new ArrayDeque<>();
            // 出队
            public void pop(Integer i){
                if (!deque.isEmpty()&&i.equals(deque.peekFirst())){
                    deque.pollFirst();
                }
            }

            // 入队
            public void push(Integer i){
                while (!deque.isEmpty()&&i>deque.getLast()){
                    deque.pollLast();
                }
                deque.offerLast(i);
            }

            // 获取队首元素
            public Integer getPeek(){
                return deque.peekFirst();
            }
        }
        public int[] maxSlidingWindow(int[] nums, int k) {
            ArrayList<Integer> list = new ArrayList<>();
            DandiaoQueue dandiaoQueue = new DandiaoQueue();
            for (int i = 0; i < Math.min(k,nums.length); i++) {
                dandiaoQueue.push(nums[i]);
            }
            list.add(dandiaoQueue.getPeek());
            for (int i = k; i <nums.length ; i++) {
                dandiaoQueue.pop(nums[i-k]);
                dandiaoQueue.push(nums[i]);
                list.add(dandiaoQueue.getPeek());
            }
            int[] ints = new int[list.size()];
            for (int i = 0; i <list.size(); i++) {
                ints[i]=list.get(i);

            }
            return ints;
        }

复杂度

时间复杂度 0（n）
空间复杂度 0（k）

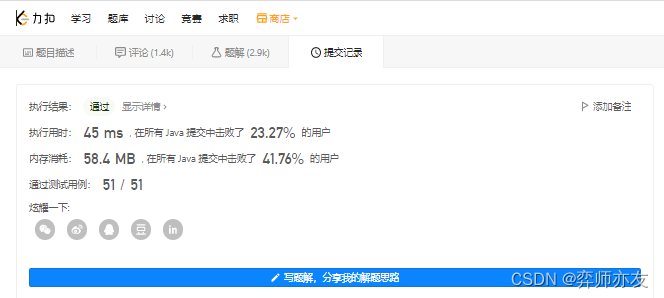
遇到的困难/进一步优化/ 收获

三刷时看一遍，敲一遍代码

347.前 K 个高频元素

看完题后的思路

先使用map统计元素的出现次数，使用一个小根堆，大小为k。如果堆的大小小于k，直接插入元素，如果比堆顶元素小，直接略过，如果比堆顶元素大，插入根堆。
大小根堆的选择：
（1）大根堆保证堆头的元素是最大元素，如果堆的大小为k，可以保证是第k小元素，其余都比它小。小根堆最终保证堆头是最小元素，如果堆的大小为k，可以保证是第k大元素
（2）根堆的大小是需要在插入元素的时候人为控制的，例如小根堆，只允许插入比堆顶元素大的元素， 此时堆顶元素被删除
在java中如何定义大根堆与小根堆
http://t.csdn.cn/OOSnB
小根堆相当于升序，返回01-02
大根堆相当于降序，返回02-01

思路

见上文

代码

 public int[] topKFrequent(int[] nums, int k) {
            HashMap<Integer, Integer> map = new HashMap<>();
            for (int num : nums) {
                map.put(num,map.getOrDefault(num,0)+1);
            }
            PriorityQueue<int[]> smallHeap = new PriorityQueue<>(new Comparator<int[]>() {
                @Override
                public int compare(int[] o1, int[] o2) {
                    return o1[1]-o2[1];
                }
            });
            for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
                int[] ele = new int[]{entry.getKey(),entry.getValue()};
                if (smallHeap.size()<k||ele[1]>smallHeap.peek()[1]) {
                    if (smallHeap.size()==k){
                        smallHeap.poll();
                    }
                    smallHeap.add(ele);
                }
            }

            int[] ints = new int[k];
            int i=0;
            for (int[] ints1 : smallHeap) {
                ints[i++]=ints1[0];
            }
            return ints;

        }

复杂度

时间复杂度： 由0（nlogn）将至0（nlogk）
空间复杂度 0（k）